海洋上行激光通信的蒙特卡罗模拟

吴方平，章 曦，杨 军，苗仁德，马书云，刘翠翠

(解放军理工大学理学院物理教研中心，江苏 南京211101)

1 引言

在水下无线光通信中，激光脉冲是目前通信信号的主要形式［1］。海洋激光雷达模型的建立是一件非常困难的工作，几乎不可能用解析法来完整地描述海洋激光雷达的返回信号;通过实验方法获取所有的数据也是不现实的，因为实验费用极其昂贵，而且在实验室条件下，由各种参数(如海水衰减系数、目标反射率等)测得的结果也受实验条件的制约［2］。实践证明［3－4］，Monte Carlo方法能够得到与实验方法极为吻合的结果。Monte Carlo方法是在对光子随机运动轨迹计算的基础上“利用相位函数、单次散射率和总衰减系数”并通过随机数选取散射位置和散射角度来构成光子轨迹模拟光在浑浊介质中传播的整个物理过程［5］。

目前对于海洋激光通信的研究大多集中在下行激光，即机载或卫星携带激光雷达对潜艇的探测问题，而关于上行激光的传输，即潜艇与海面或空中接收雷达的通信研究文献较少。本文在现有文献［6－7］对上行激光的传输研究的基础上，进一步分析了上行激光通信中接收光子数目和空间分布与目标深度和海面风速的关系，以及接收光子相对能量的径向分布情况。

2 上行激光海洋信道光传输的蒙特卡罗模拟

上行激光的蒙特卡罗模拟包括潜艇发射光子束，光子束与水体的相互作用(吸收与散射)，光束出水共三个步骤。

2．1 发射光子束

在蒙特卡罗方法的源抽样处引入了高斯分布抽样模型，使发出光子的统计特性满足高斯光束的特性［8］。

式(1)中的x和y分别代表垂直于激光光束传输方向的平面上的横坐标和纵坐标，σs为激光光束的均方根半径，通常称为光斑尺寸，用来描述光束的径向分布。

2．2 光子束与水体的相互作用

光子束与水体的作用包含散射与吸收两部分。设海水的体积衰减系数为c，则光子每一步的几何路径长度为L=－ln(rand1)/c，其中rand1为［0，1］区间内均匀分布的随机数。设水体的单次散射率为ω0，取［0，1］区间内均匀分布的随机数rand2，如果rand2＞ω0，则认为光子被吸收，终止对该光子的跟踪，反之则认为光子被散射［9］。光子与水体粒子作用后，新的权值为:

光子发生散射后，新的传播方向由散射相函数决定。这里采用Henyey-Greenstein函数来近似表示其散射相位概率函数［10］:

其中，g是非对称因子;θ为散射角。

2．3 光束出水

光束出水时经历海气界面的三维折射。海面的法线方向具有随机性，但也具有一定的规律性，Charles Cox等［11］给出了海浪在一定风速下俯仰角β的经验归一化概率密度公式为:

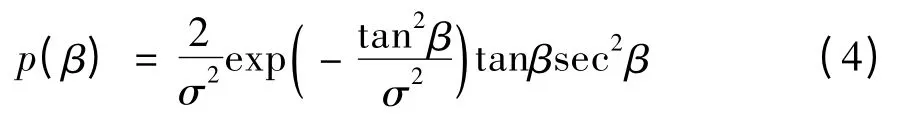
其中，均方根表面速率σ=(0．003+0．00512v)1/2，v为风速，由此可以选用舍选抽样法对其进行抽样，得到俯仰角β的值，从而判定是否发生全反射及确定光束的出水方向。

3 模拟结果及分析

模拟发出的光子总数为106个，取接收光子束的飞机高度为H=200 m，并位于发射光子束的潜艇正上方，光子接收平面为潜艇正上方的海水区域。

潜艇深度MD分别取5 m，10 m，15 m，20 m，海面风速分别为v=5 m/s，10 m/s，15 m/s，30 m/s，采用舍选抽样法进行Monte Carlo模拟。初始高斯光束半径为0．5 m。海水衰减系数c=0．5，单次散射率ω0=0．6，目标反射率ρ=0．7，非对称因子g=0．5。

3．1 风速一定时，潜艇深度对接收光子的影响

风速v=15 m/s，潜艇深度MD=5 m，10 m，15 m，20 m时，接收光子数目和接收光子总权值的模拟结果如表1所示。

表1 风速v=15 m/s，潜艇深度MD=5 m，10 m，15 m，20 m时，接收光子数与接收光子总权值Tab．1 The numbers of received photons and the net weights of received photons when wind speed v=15 m/s and submarine depths MD=5 m，10 m，15 m，20 m，respectively

由表1可知，在相同风速条件下，潜艇深度对接收光子数目和接收光子总权值影响很大，随着潜艇深度的增加，接收光子数及接收光子总权值急剧下降，并且潜艇深度对接收光子总权值的影响要大于对接收光子数目的影响。

为了清晰地反映接收光子的空间分布，我们分别绘制了在上述条件下，接收光子的二维分布图和三维分布图，结果如图1和图2所示。

由图1可知，风速一定时，虽然接收光子数目随着潜艇深度的增加而锐减，但接收平面上的光子分布是对称的，体现了大量随机运动的光子整体仍遵循统计规律，并且接收光子均主要集中在x=±10 m，y=±10 m区域。

图1 风速v=15m/s，潜艇深度MD为(a)5 m，(b)10 m，(c)15 m和(d)20 m时，接收光子二维分布图Fig．1 The two-dimensional distribution of received photons when v=15 m/s and submarine depths MD equal(a)5 m，(b)10 m，(c)15 m，(d)20 m，respectively

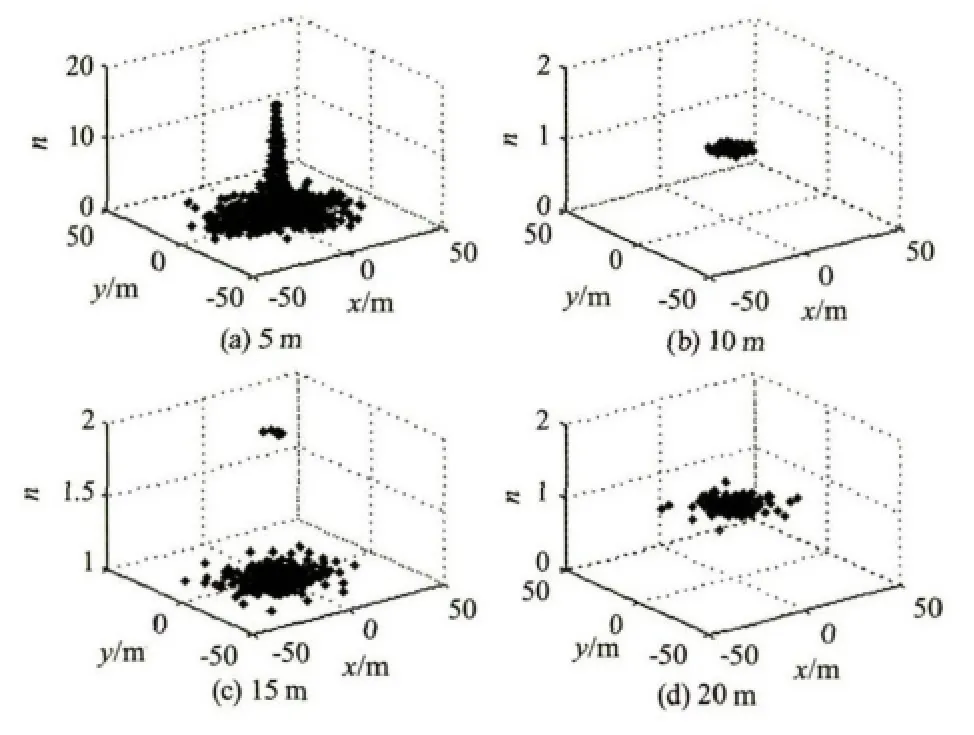
图2 风速v=15 m/s，潜艇深度MD为(a)5 m，(b)10m，(c)15 m和(d)20 m时，接收光子数目三维分布图Fig．2 The three-dimensional distribution of received photons when v=15m/s and submarine depths MD equal(a)5 m，(b)10 m，(c)15 m，(d)20 m，respectively

由图2可知，在潜艇深度较浅(5 m)时，接收平面上的光子分布仍接近高斯分布，但随着潜艇深度的增加，接收光子在接收平面上的分布逐渐趋于均衡，这说明潜艇深度的增加导致光子运动的随机性增加。

3．2 潜艇深度一定时，风速对接收光子的影响

潜艇深度MD=10 m，风速v=5 m/s，10 m/s，15 m/s，30 m/s时，接收光子数目和接收光子总权值的模拟结果如表2所示。

由表2可知，潜艇深度一定时，风速对接收光子数目和接收光子总权值的影响不大，而且并无明显的规律，接收光子数和接收光子总权值并没有随风速的增加单调递增或递减，这说明风速的影响不占主导地位，这与文献［11］结论相同。

表2 潜艇深度MD=10 m，风速v=5 m/s，10 m/s，15 m/s，30 m/s时接收光子数和接收光子总权值Tab．2 The numbers of received photons and the net weights of received photons when submarine depths MD=5 m，and wind speed v=5 m/s，10 m/s，15 m/s，30 m/s，respectively

图3和图4分别为上述条件下，接收光子的二维分布图和三维分布图。

图3 潜艇深度MD=10 m，风速v为(a)5 m/s，(b)10 m/s，(c)15 m/s和(d)30 m/s时接收光子二维分布图Fig．3 The two-dimensional distribution of received photons when submarine depths MD=5 m，and wind speed v equal(a)5 m/s，(b)10 m/s，(c)15 m/s，(d)30 m/s，respectively

对比图3和图1，可以发现接收光子分布的对称性和分布范围两者是基本一致的，这说明光子运动的随机性基本不受风速和潜艇深度的影响。

图4 潜艇深度MD=10 m，风速v=5 m/s，10 m/s，15 m/s，30 m/s时接收光子数三维分布图Fig．4 The three-dimensional distribution of received photons when submarine depths MD=5 m，and wind speed v equal(a)5 m/s，(b)10 m/s，(c)15 m/s，(d)30 m/s，respectively

图4表明，风速对接收光子的空间分布影响不大，同样说明风速的影响不占主导地位。

3．3 风速与潜艇深度对接收平面处光子相对能量径向分布的影响

取潜艇正上方为圆心，风速v=15 m/s，潜艇深度MD=5 m，10 m，15 m，20 m时，接收平面处光子相对能量径向分布如图5所示，潜艇深度MD=10 m，风速v=5 m/s，10 m/s，15 m/s，30 m/s时，接收平面处光子相对能量径向分布如图6所示。

图5 风速v=15 m/s，潜艇深度MD=5 m，10 m，15 m，20 m时，接收平面处光子相对能量径向分布Fig．5 The radial distribution of received photons’relative energy when wind speed v=15 m/s and submarine depths MD=5 m，10 m，15 m，20 m，respectively

图5 (a)显示，风速一定时，对于相同的相对能量，潜艇深度越低，对应的区域半径越小，而图5(b)显示，这一规律在相对能量较大处被打破，意味着光子径向分布半径较大处，光子运动的随机性受潜艇深度影响较小。

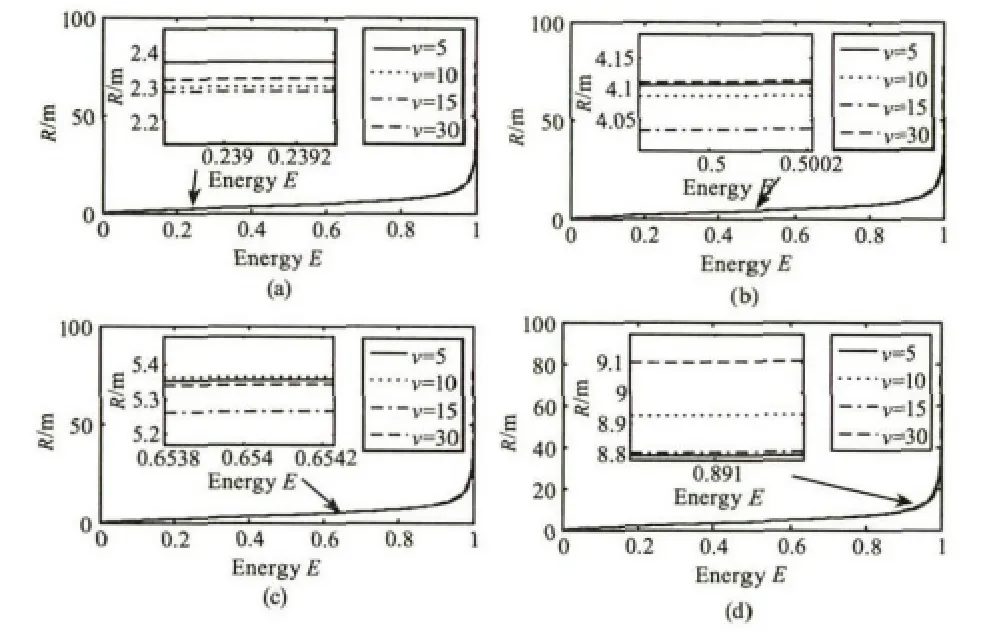
图6 潜艇深度MD=10 m，风速v=5 m/s，10 m/s，15 m/s，30 m/s时，接收平面处光子相对能量径向分布Fig．6 The radial distribution of received photons’relative energy when submarine depths MD=5 m，and wind speed v=5 m/s，10 m/s，15 m/s，30 m/s，respectively

图6 表明，相同潜艇深度时，风速对接收平面处光子相对能量径向分布的影响并无明显规律，在不同相对能量处，四种风速对应的区域半径排序各不相同，这同样意味着风速对光子运动的影响不起主导作用。

4 结论

通过蒙特卡罗方法数值模拟，在相同风速条件下，随着潜艇深度的增加，接收光子数急剧下降，并且只在潜艇深度较浅时，接收平面上的光子分布才接近高斯分布。潜艇深度一定时，风速对接收光子数目以及接收光子的空间分布影响不大。风速一定时，对于相同的相对能量，潜艇深度越低，对应的区域半径越小，而相同潜艇深度时，风速对接收平面处光子相对能量径向分布的影响并无明显规律。

［1］ ZHOU Yamin，WU Keqi，CHEN Jinlai，et al．Monte Carlo simulation of time domain broadening of laser pulse propagating underwater［J］．Laser＆Infrared，2011，41(3):259－263．(in Chinese)周亚民，吴克启，陈金来，等．激光脉冲水下传输时域展宽的蒙特卡罗模拟［J］．激光与红外，2011，41(3):259－263．

［2］ DU Zhufeng，LU Yimin，YANG Zongkai，et al．Monte Carlo calculations of the received oceanic lidar signals［J］．Chinese Journal of Lasers，1999，26(1):52－56．(in Chinese)杜竹峰，卢益民，杨宗凯，等．海洋激光雷达接收信号的Monte Carlo计算［J］．中国激光，1999，26(1):52－56．

［3］ G Zaccanti，P B ruscaglioni，M Gurio li，et al．Laboratory simulations of lidar returns from clouds:ex2 perimental and numerical results［J］．Appl．Opt．，1993，32(9):1590－1597．

［4］ K O Steinvall，K R Kopparl，U C M Karlsson．Experimental evaluation of an airborne depthsounding lidar［J］．Opt．Eng．，1993，32(6):1307－1321．

［5］ JIANG Lu，ZHU Hai，YU Yunzhi．Optical concealment analysis of underwater target based on Monte Carlo method of simulation［J］．J．Projectiles，Rockets，Missiles and Guidance，2006，26(4):401－404．(in Chinese)姜璐，朱海，于运治．基于蒙特卡罗方法的水下目标光隐蔽性影响因素分析［J］．弹箭与制导学报，2006，26(4):401－404．

［6］ LIU Jintao，CHEN Weibiao．Uplink laser communications between a satellite and a submerged platform［J］．Acta Photonica Sinica，2010，39(4):693－698．(in Chinese)刘金涛，陈卫标．水下平台对卫星上行激光通信研究［J］．光子学报，2010，39(4):693－698．

［7］ ZHOU Tianhua，CHEN Weibiao，HE Yan，et al．．Beam spatial distribution of upward laser through sea air interface［J］．Chinese Journal of Lasers，2010，37(8):1978－1982．(in Chinese)周田华，陈卫标，贺岩，等．通过海气界面的上行激光光场分布［J］．中国激光，2010，37(8):1978－1982．

［8］ ZHANG Xi，LI Peijun，WU Fanging，et al．Influence of wavy sea surface on laser detection of underwater target with Monte Carlo method［J］．Chinese Journal of Lasers，2012，39(7):0702003－1～0702003－5．(in Chinese)章曦，李配军，吴方平，等．基于蒙特卡罗方法的波动水面对激光水下目标探测的影响［J］．中国激光，2012，39(7):0702003－1～0702003－5．

［9］ WU Fangping，ZHANG Xi，LI Peijun，et al．Monte carlo simulation analysis of underwater target detection by oceanic lidar［J］．Laser＆Optoelectronics Progress，2012，49(12):121401－1－121401－7．(in Chinese)吴方平，章曦，李配军，等．海洋激光雷达水下目标探测的蒙特卡罗仿真分析［J］．激光与光电子学进展，2012，49(12):121401－1－121401－7．

［10］E Tinet，SAvrillier，JM Tualle．Fast semianalytical monte carlo simulation for time-resolved light propagation in turbid media［J］．J．Opt．Soc．Am．A，1996，13(9):1903－1915．

［11］C SCox，W Munk．Measurement of the roughness of the sea surface from photographs of the sun’s glitter［J］．J．Opt．Soc．Am，1954，44(11):838－850．