Meissel-Stokes核函数应用于区域大地水准面分析
荣 敏,周 巍,任红飞
(1.信息工程大学 地理空间信息学院,河南 郑州450052;2.西安测绘研究所,陕西 西安710054;3.西安测绘总站,陕西 西安710054)
精化大地水准面是满足大地测量和诸多地球科学发展需要的一项重要工作。Stokes理论框架下建立边值问题计算大地水准面时,理论上需要在全球范围内进行求解[1-2]。但由于测量数据、成本以及计算效率等多个方面的原因,实现全球积分不太可能[3-4]。为了解决此问题,提高计算精度,有关学者提出多种改善方式,通常是将积分域分为球冠(近区)和剩余部分(远区)[3-4],近区应用Stokes公式积分计算,忽略其远区影响。再者是基于高精度地球重力场模型,采用移去-恢复法,移去重力场中的低频(长波)影响[5]。在此基础上,还可考虑采用修正St okes核函数,改善标准Stokes特性,提高近区计算能力,减弱其远区效应等。
较早的修正Stokes核函数理论有:M.S.Molodensky(1962)、Wong和Gore(1969),以及Meissl(1971)等[6-15]。2003年,Michael Kern对于多种修正Stokes核函数,基于EGM96和GPM98B进行研究分析,认为Meissel-Stokes具有计算速度快、实现方便、远区影响小等特点[11]。2013年,傅露等结合DNSC08-CRA模型中的美国重力数据,分析比较几种修正Stokes核函数,得出采用修正Stokes核函数 可有效改善计算精度 其中Meissel-Stokes核函数,计算简单,速度较快,是一种较优的修正Stokes核函数[12]。2007年,李建成提出在厘米级精度要求下,重新研究Stokes核函数和构造截断函数问题[3-4]。研究修正Stokes核函数,是实现建立厘米级精度大地水准面的主要理论问题和关键技术之一。文献[16]中认为使用标准Stokes核函数会遗漏部分长波影响,而引入误差。因此,本文基于EGM2008地球重力场位系数模型,分析讨论Meissel-Stokes和标准Stokes核函数特性,并利用它们计算大地水准面差距,比较两者计算大地水准面精度,用以精化区域大地水准面。
1 大地水准面计算
应用Stokes公式计算大地水准面差距N的表达式为[1-2]

式中:R为地球平均半径;γ0为正常重力异常;Δg(R,Ω′)为大地水准面上的重力异常值;Ω′为积分面;dΩ′=sinϑ′dϑ′dλ′=sinψdψdα;ϑ′和λ′为积分点余纬和经度;ψ为计算点与积分点之间的角距;α为计算点至积分点方向的方位角。
标准Stokes核函数为[15]

通常将积分区域划分为近区和远区,即Ω0为近区,Ω-Ω0为远区,则式(1)可重新表达为

采用移去-恢复法,移去地球重力场模型,计算至n=L阶时的重力异常值ΔgL,获取剩余重力异常值Δgres,计算剩余大地水准面差距Nres,其算式为

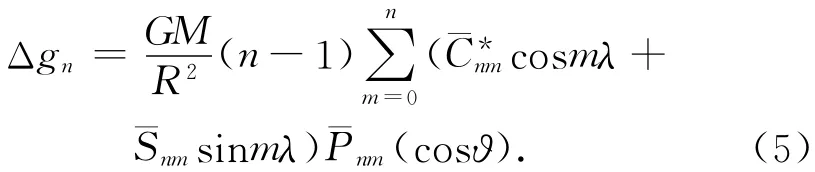
利用地球重力场位系数模型,模型重力异常Δgn的算式为式中:GM为地心引力常数;Cnm和Snm为完全正常化的球谐系数;¯Pnm(cosϑ)是完全规格化缔合Legendre函数;ϑ和λ分别为地心纬度和经度;n和m分别为地球重力场模型的阶与次。
近区,当ψ=0°时,Stokes积分式存在弱奇异。求解该问题时,需要做一小变化,用以减弱奇异计算,则近区大地水准面差距的计算公式,可表示为

Q0为零阶截断误差系数,则有

远区效应,一般考虑使用地球重力场位系数模型计算,算式为

式中:ψ0为截断积分半径;εn为重力场位系数误差;Qn(ψ0)为截断误差系数,其算式为

式中:Pn(cosψ)为Legendre多项式。
远区效应的计算误差主要由地球重力场位系数误差和截断误差组成。重力场模型位系数误差是随着重力场模型生成而存在,属于已知量。截断误差是指模型阶次截断至L阶所引起的误差,是远区效应的主要影响量。截断误差小,远区效应就小,则在一定精度下可忽略其影响。
2 Meissel-Stoke核函数S M(ψ)应用于大地水准面计算
1966年,De Witte发现在原Stokes核函数零交点处的截断误差比较小。基于该理论,1971年Meissel给出了Meissel-Stokes公式[9-15],则有

近区,将式(12)代入式(6),替换原标准Stokes核函数,则有

远区效应δNM的计算表达式为[9-15]

式中:Qmn(ψ0)为Meissel-Stokes核函数相应的截断误差系数。
Meissel-Stokes截断误差系数计算式中,应用Legendre多项式循环迭代关系,其截断误差收敛速度较快,尤其在采用移去-恢复法时效果明显。
3 精度检测
利用EGM2008重力场位系数模型和实验区内的重力点数据,评价Meissel-Stokes核函数应用于区域大地水准面差距计算。首先,计算重力点移去L=120阶,计算至360阶的重力异常模型值,作为残余重力异常值Δg121-360然后 基于重力点的残余重力异常值,生成2.5′×2.5′格网值;接着,采用Stokes公式,计算残余大地水准面差距Nres,经恢复,获得大地水准面差距N′360;最后,以EGM2008位系数模型,n=2~360获得的NM360为真值,求差值δN,统计其精度,具体的计算过程见式(17)、式(18)。
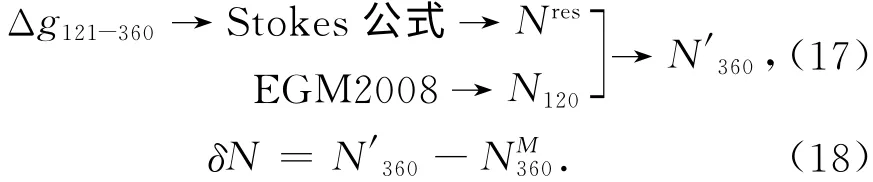
差值δN当中包含远区效应的截断误差、重力场模型位系数引入的误差,以及重力数据格网化和积分离散化误差。
4 计算与分析
为评价Meissel-Stokes核函数在区域大地水准面精化中的应用,首先,分析核函数和截断误差系数与积分半径及模型阶次关系;然后,计算分析两重力点截断误差随积分半径的变化。
4.1 核函数和截断误差系数分析
基于EGM2008地球重力场位系数模型,分析标准Stokes核函数和Meissel-Stokes核函数与截断积分半径关系,如图1所示。分别取截断积分半径为1°,3°,6°和12°,其截断误差系数,随重力场位系数模型阶次变化情况,如图2所示。
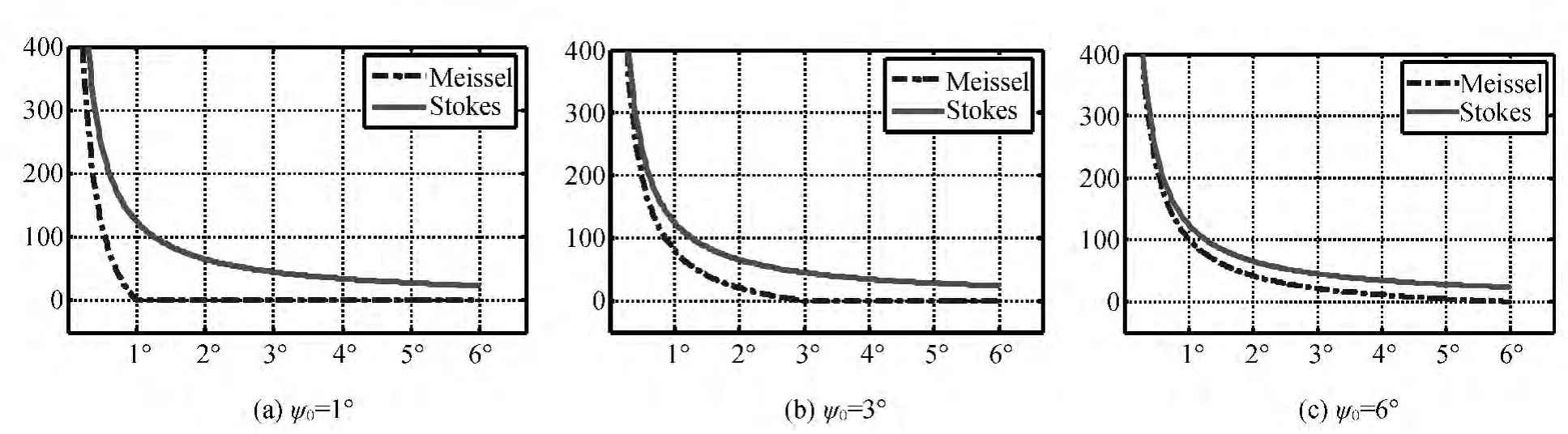
图1 核函数随0°≤ψ≤6°的变化
由图1可见,Meissel-Stokes函数和标准Stokes核函数,都随着球面角距的增加,其值逐渐减小;当球面角距在0.5°范围以内,核函数值变化较为剧烈;当球面角距大于0.5°时,其相对平缓。Meissel-Stokes函数收敛速度快于标准Stokes核函数。截断积分半径越小,Meissel-Stokes函数值变化越大,与Stokes核函数的差异也相对较大。
由图2可见,Meisel-Stokes截断误差系数,截断积分半径为1°时,其截断阶次在120阶收敛至0附近;截断积分半径为3°和6°时,其截断阶次大致在70阶,收敛至0附近。当截断积分半径为12°时,在大约20多阶,收敛至0附近。
整体上,模型截断阶次越高,则截断误差系数值越小,并随之逐渐稳定。截断积分半径越大,收敛速度越快。当截断阶次L≥120阶时,Meissel-Stokes的截断误差系数值都在0附近。而标准Stokes核函数计算值,相对变化剧烈,其大都取至L≥180时,相对稳定。

图2 截断误差系数随模型阶次的变化
4.2 截断误差分析
在实验区,选取两个重力点,具体情况见表1。利用EGM2008重力场位系数模型,分析标准Stokes和Meissel-Stokes核函数,截断至L=120时,分别取截断积分半径为1°,3°和6°,截断误差随着模型阶次的变化见图3所示。
由图3可见,随着截断半径增加,截断误差值减小。基于Meissel-Stokes核函数的截断误差,相对标准Stoke核函数的计算值,要稳定且量值要小。标准Stokes核函数计算的截断误差,在后相对稳定。地形高也对截断误差略有影响。由此可见,采用Meissel-Stokes核函数,解算至120阶,其截断误差影响趋于稳定。

表1 截断误差计算点


图3 截断误差图(m)
4.3 Meissel-Stokes核函数应用分析
实验区位于北纬28°~32°,东经108°~114°,东部较为平坦,西部为多山区。其中分布有8 564个实测重力点值,高程最大值为2 890.5 m,最小值为18.2 m,平均值为233.4 m。实际地形见图4。

图4 实验区地形图
为评价Meissel-Stokes核函数,利用EGM2008地球重力场位系数模型,截断至L=120阶,计算实验区内,大地水准面上的残余重力异常模型值,并生成2.5′×2.5′格网值,统计值见表2。

表2 基于EGM2008模型的实验数据统计表 mGal
选用积分半径为1°,截断阶次为L=120,计算残余大地水准面差距,统计结果见表3。恢复后,获得的大地水准面差距结果,统计情况见表4;图5(a)为L=360阶,EGM2008模型计算的大地水准面差距;图5(b)为由标准Stokes核函数,计算获得大地水准面差距;图5(c)为由Meissel-stokes核函数,计算的大地水准面差距。统计大地水准面差距的偏差,结果见表5。
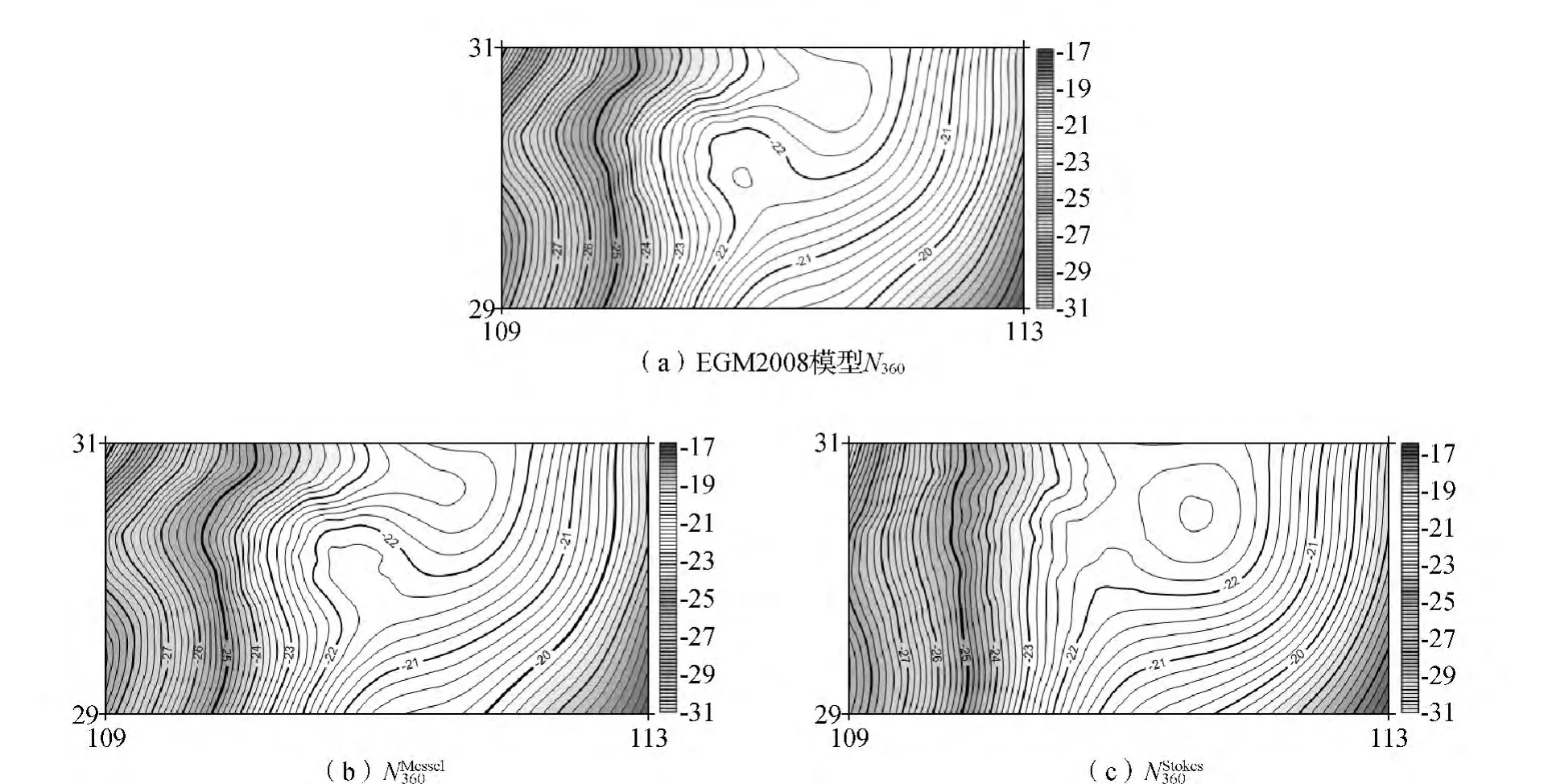
图5 大地水准面差距图(m)
由图5可见,基于标准Stokes和Meissel-Stokes核函数计算的大地水准面差距都与模型值趋势接近;但相对而言,标准Stokes核函数计算的大地水准面差距与模型值的差异明显。

表3 剩余大地水准面差距计算值统计 m

表4 大地水准面差距计算值统计 m

表5 大地水准面差距计算值与模型值的偏差统计表m
由表3~表5可知,基于标准Stokes核函数,移去L=120,计算大地水准面差距值,比EGM2008模型值小;最大相差大约0.8 m;平均值相差0.02 m以内。基于Meissel-Stokes核函数,计算的大地水准面差距,较模型值偏大;最大相差在大约0.2 m;平均值相差大约0.01 m。基于Meissel-Stokes核函数,采用1°积分半径,较标准St okes核函数计算的大地水准面差距,标准偏差小。
由表5可知,利用Stokes和Meissel-Stokes核函数计算的大地水准面差距,与模型值存在偏差。究其原因一是截断积分半径和截断阶次有限性;二是截断误差较大;三是地球重力场位系数误差;四是重力点数据分布不均匀,格网化时引入了误差;五是Stokes积分离散化误差引入的误差等。但相对而言,Meissel-Stokes计算精度比Stokes计算精度要好。
5 结束语
基于EGM2008重力场位系数模型,精化区域大地水准面计算时,认为截断至120阶以上,积分半径≥6°时,可忽略其远区效应。而实际上,由于测量数据有限性,很难达到所需的积分半径要求,因此可考虑选用Meissel-Stokes核函数,它收敛速度快,截断误差小且稳定。相同条件下,采用Meissel-Stokes计算大地水准面差距,其精度比标准Stokes核函数计算大地水准面的精度高。由此可见,在大地水准面精化工作中,采用移去-恢复法,应用Meissel-Stokes核函数,可提高大地水准面的计算精度,为实现建立厘米级精度大地水准面这一目标服务。
[1] 陆仲连.地球重力场理论与方法[M].北京:解放军出版社1996年.
[2] HOFMANN-WELLENHOF B,MORITZ H.Physical geodesy[M].second edition,Springer Wien New Yor k,2006.
[3] 李建成.我国现代高程测定关键技术若干问题的研究及进展[J].武汉大学学报:信息科学版,2007,32(11):980-987.
[4] 李建成.最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J].测绘学报,2012,41(5):651-660,669.
[5] 刘晓刚,刘雁雨,曹纪东,等.GPS水准采用移去-恢复技术拟合大地水准面方法的研究[J].测绘工程,2008,17(3):70-73.
[6] 魏子卿,王刚.用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J].测绘学报,2003,32(1):1-5.
[7] 傅露,褚永海.区域大地水准面确定中Stokes核函数的应用[J].大地测量与地球动力学,2013,33(2):110-113,119.
[8] FEATHERSTONE W E,EVANS J D,OLLIVER J G.A Meissl-modified Vanicek and Kleusberg kernel to reduce the truncation error in gravi metric geoid computations[J].Journal of Geodesy,1998,72:154-160.
[9] SJÖBERG L E,HUNEGNA W A.Some modifications of Stokes for mula the account for truncation and potential coefficient errors[J].Journal of Geodesy,2000,74:232-238.
[10]SJÖBERG L E.A computational scheme to model the geoid by the modified Stokes f or mula without gravity reductions[J].Journal of Geodesy,2003,77:423-432.
[11]ELL MANN A.Two deter ministic and three stochastic modifications of Stokes’s f or mula:a case study f or the Baltic countries[J].Journal of Geodesy,2005,79:11-23.
[12]VANICEK P,FEAT HERSTONE W E.Perfor mamce of three types of Stokes’s ker nel in the combined solution f or the geoid[J].Journal of Geodesy,1998,72:684-697.
[13]EVANS J D,FEATHERSTONE W E.Improved convergence rates f or the tr uncation error in gravimetric geoid deter mination[J].Journal of Geodesy,2000,74:239-248.
[14]KERN M.An Analysis of the Combination and Downward Continuation of Satellite,Airborne and Terrestrial Gravity Data[R].Canada:University of CALGARY,2003.
[15]SPRLAK M.Generalized geoidal estimators f or deterministic modifications of spherical Stokes’f unction[J].Contributions to Geophysics and Geodesy,2010,40(1):45-64.
[16]WANG Y M,SALEH J,LI X,et al.The US Gravimetric Geoid of 2009(USGG2009):model develop ment and evaluation[J].Journal of Geodesy,2012,86:165-180.

