桥轴线拟合的分期回归方法

徐 兮

(1．重庆电讯职业学院，重庆630342;2．重庆交通大学，重庆400074)

一、引 言

对历史悠久的文物桥或“超期服役”的老旧桥进行安全、健康诊断，是一项严谨和必需的工作，常规的措施是将设计、施工资料与变形测量数据进行比较分析，提出经济适用的维修养护方案并加以执行，以保障桥梁在稳定的状态下能够良性运通。而文物桥、老旧桥大多年代久远，其设计、施工资料因社会变革或战火动乱大多荡然无存，这就给相关活动的开展带来了不小的困难。

民国时期建筑，延用至今的重庆市江津区SF拱桥，设计施工资料全部缺失，设计寿命无法查得，为保障运通的安全，从20世纪80年代起，每10年对该桥进行了一次全面监测。在SF桥最近一次的健康诊断工作中，笔者负责数据处理分析工作，期间，在原始资料缺乏的情况下采用分期回归方法，完成了该桥的变形分析判断任务。

二、测量方法与观测数据

分别建立以三孔左拱脚为原点、两拱脚的连线为x轴、与x轴垂直方向(桥高)为y轴的坐标系(如图1所示);对3个孔进行变形观测，但由于3个孔的观测方法及后续分析方法等完全相同，本文仅对中孔展开讨论。

为了确定中孔拱轴线形态，按常规要在中孔拱轴线上预先设定一定数量的等间隔的标志点，而此项操作却极其困难。为了不设定这种标志，以及在桥面上便于进行测角、量距，首先在拱脚两点且与拱脚连线相垂直的直线方向的地面上，任意选C1、C2点，分别安置经纬仪，瞄准两拱脚点，抬高望远镜，在桥上定出两拱脚点的投影点O'、O″，在拱脚线外的任一点C处立标志，测出β1、β2角及O'、O″之距离DO'O″，即可求出C至O'的平距d0。(如图2(a)所示)。

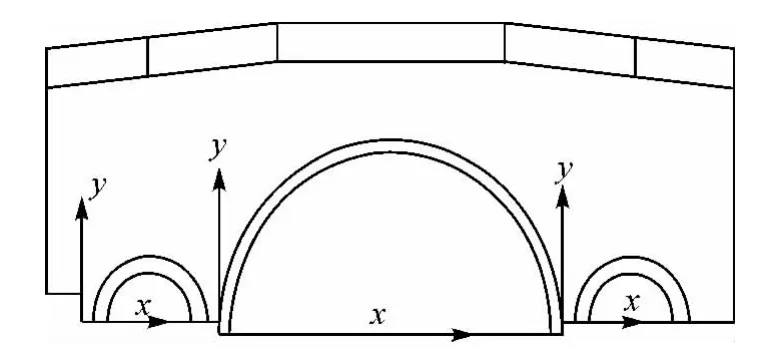
图1 坐标示意图

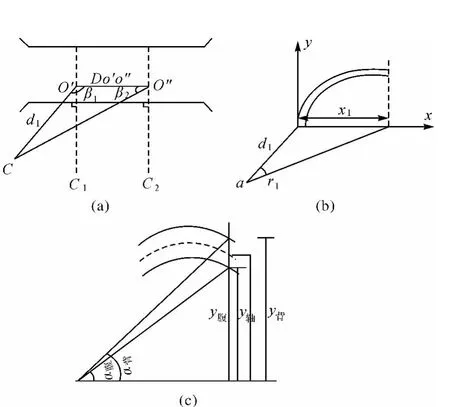
图2 观测示意图

将DO'O″25等分得25个截面，算出O'至每一截面的平距，即求出了每一截面的x坐标(见表1)。根据d0、β1和任意截面的xi，可求出以O为后视方向该截面应有的平角ri，以及截面与C点的距离di。在C点安置经纬仪，后视O(水平盘归零)，转动照准部至水平盘得ri值，水平制动后抬高望远镜，分别瞄准拱腹、拱背，读出竖盘读数，计算出αi腹、αi背，再采用di值，即可求出yi腹、yi背，取其均值即为该截面与孔轴线之交点的纵坐标值yi(如图2(b)、(c)所示)，列于表1的x、y。

三、分期回归建模

1．数学推演

通过以前对该桥的变形分析已知，桥拱为圆曲线型

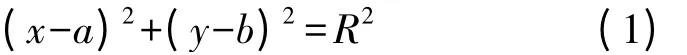
式中，(a，b)为圆心坐标;R为半径。经分解变换，得圆一般方程为

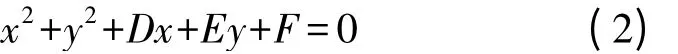
式中，D、E、F为参数。为求D、E、F，分别将(x1，y1)、(x2，y2)、(x3，y3)代入式(2)，得方程组

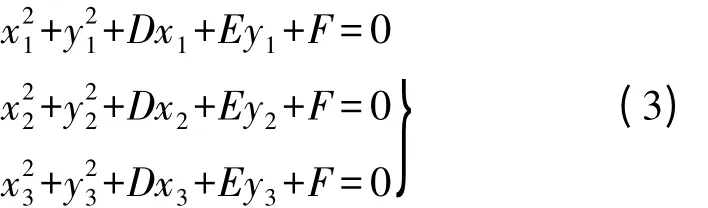
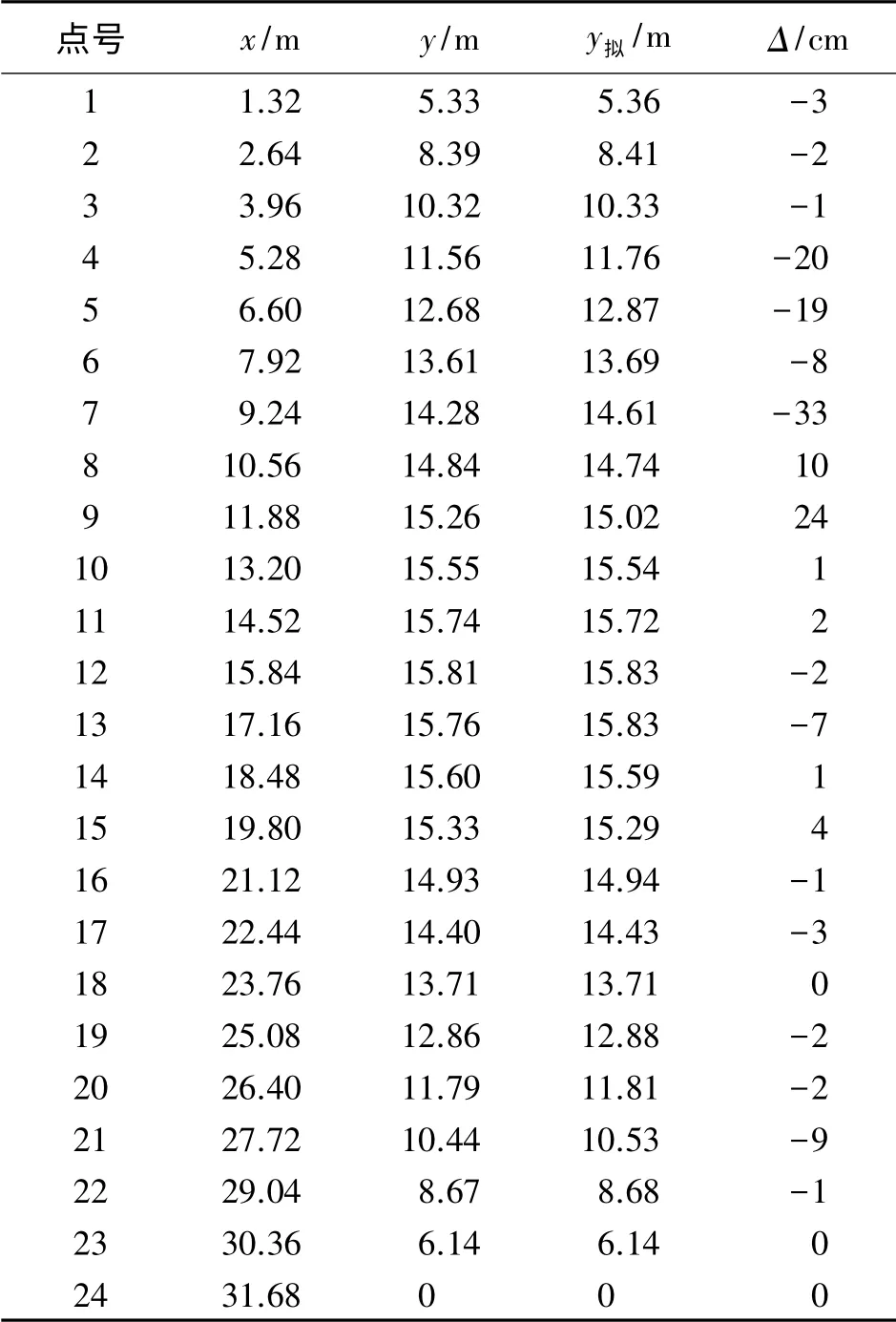
表1 数据表

应用代入法整理式(3)，求出

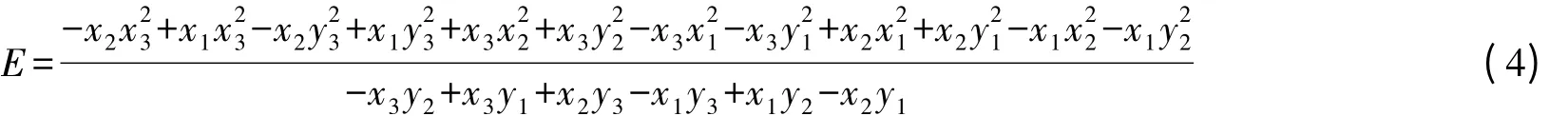
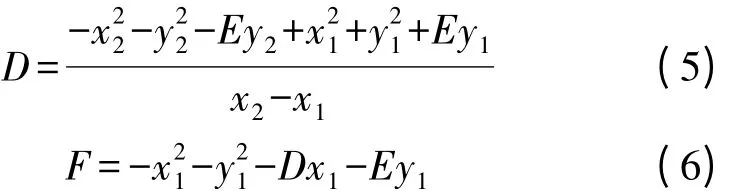
通过分解化简等互换式(1)和式(2)，a、b、R可用D、E、F表示

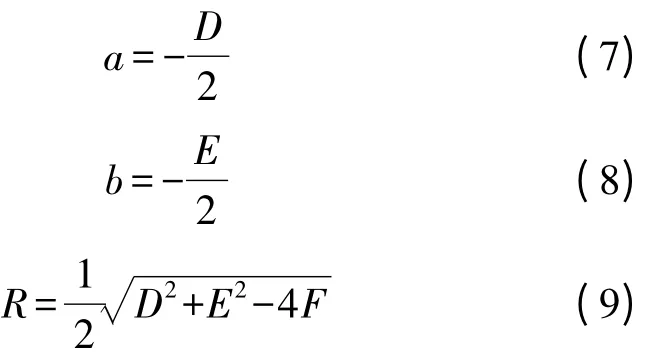
整理式(1)，得y的计算式

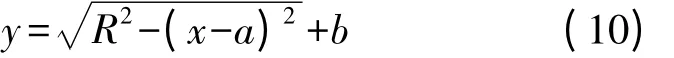
模型有效与否，采用相关性检验

残差算式

2．第一期回归

将表1第1、2、3点的观测数据分别代入式(4)—式(6)，求出D=－30．87，E=－2．11，F=21．86，将上述值代入式(7)—式(9)，计算出a=15．43，b=1．06，R=14．75，则第一期回归模型为

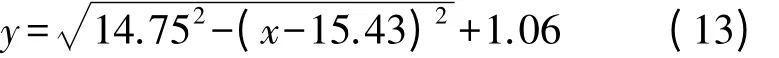
应用式(11)求得式(13)的相关性系数r=0．970，查相关性系数表得其临界值ra=0．917，r＞ra，第一期回归模型成立。

将1、2、3点的x值代入第一期模型即式(13)，分别求出1、2、3点的拟合值y拟;应用式(12)分别求出1、2、3点的残差，均填入表1相应栏。

3．各期回归

同理同法，分别以3个点为一期(如3、4、5，5、6、7，7、8、9，…)，将相关数据先后代入式(4)—式(9)，拟合出本期模型，之后应用式(11)与相关性系数表进行检验、应用式(12)求出各残差，并用相关数据续填表1，模型汇总见表2。

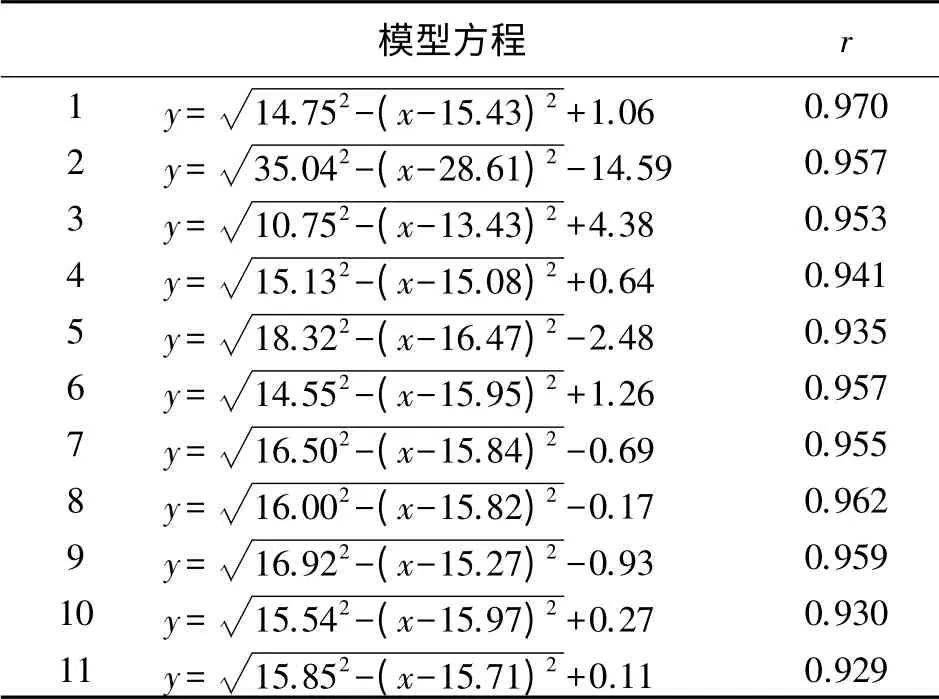
表2 模型汇总表

4．拟合曲线

以x为横标、y为纵标绘制桥拱轴线形态图(如图3所示)。

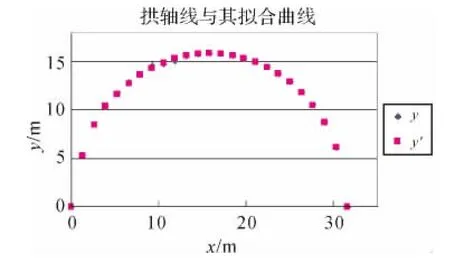
图3 桥拱轴线形态图

四、分 析

表2中各模型的相关性系数r值均大于临界值ra=0．917，表明各期模型均有效，进而证明本例回归方法正确且满足精度。

表1中4—9点的残差Δ较大，最大达到33 cm，而对应的2、3、4期模型的相关性系数r并未超限，肉眼观察桥拱4—9点弧段，发现风化现象，因而基本可以断定4—9点Δ值偏大的原因，是由于对应弧段风化较严重引起，制定维护方案时应注意该问题。

21点的Δ值为9 cm，与前后相邻数据比较显然存在异常，加之建模时使用了21点的数据，使10、11期模型的r值变小，可以认为21点观测值包含粗差。

综上分析同时由图3可看出，本例桥孔不仅依然保持圆弧拱形态，而且整体稳定，无大的形变，略加维修可正常使用。

五、结束语

本文采用分期回归理论方法，在设计、施工原始资料不存在的情况下，对老旧桥进行了变形监测数据处理和分析，建立了回归分析模型，结果证明该方法切实可用。

［1］ 周水兴．桥梁工程［M］．2版．重庆:重庆大学出版社，2011．

［2］ 张彬．桥梁工程施工速学手册［M］．北京:中国电力出版社，2009．

［3］ 岳建平，田林亚，变形监测技术与应用［M］．北京:国防工业出版社，2007．

［4］ 白凤山，么焕民．数学建模［M］．哈尔滨:哈尔滨工业大学出版社，2003．

［5］ 王金岭，陈永奇．论观测法的可靠性质量［J］．测绘学报，1994，23(4):252-258．