基于DTM 离散模型的露天矿测量验收方法

李 娜 邵必林 李角群 吕康亭

(1.西安建筑科技大学材料与矿资学院，陕西 西安710055;2.西安建筑科技大学管理学院，陕西 西安710055)

目前，测量验收主要采用的计算方法有断面法、块体模型法及三维实体模型法［1］。断面法［2-3］的误差主要来自于台阶高度的计算及剖面间距的确定;块体模型法［4-5］可根据块体中心位置判断相应块体是否已被采出，由规则块体模拟不规则的连续块体，在计算极不规则矿体时，离散误差较大;三维实体模型法［6-8］计算精确，但实体模型必须完全闭合才能进行布尔运算，存在建模复杂、计算速度慢，不稳定等问题。为此，采用DTM 离散模型进行测量验收计算，以提高计算精度。

1 DTM 离散模型

1.1 模型原理

DTM 离散模型是在DTM 的水平方向进行离散，在垂直方向仅记录水平离散块中心点的DTM 高程。DTM 离散模型既区别于块体模型在水平及垂直方向的完全离散，也有别于三维实体模型的完全连续，因而既具有块体模型结构简单、计算快速的特性，又能保证较高的计算精度及稳定性。DTM 是由无数三角面构筑而成［9-11］，故DTM 的离散化可转化为三角面的离散化，步骤为:①利用重心法则计算出落在三角面内的小矩形;②根据DTM 离散算法计算出每个小矩形的中心点高程。

1.2 模型构建

在建立DTM 离散模型之前，应首先建立DTM。在AutoCAD 软件中，构建DTM 的首选平面图元是三角面［12-13］，故DTM 的建立可转化构建三角网。三角剖分的最常用算法为Delaunay 算法［14-16］，其代表算法主要有分割-归并法［17-18］、逐点插入法和三角网生长法［19-20］。本研究选取算法较简单、占用资源较少的逐点插入法构筑三角网，步骤见图1。

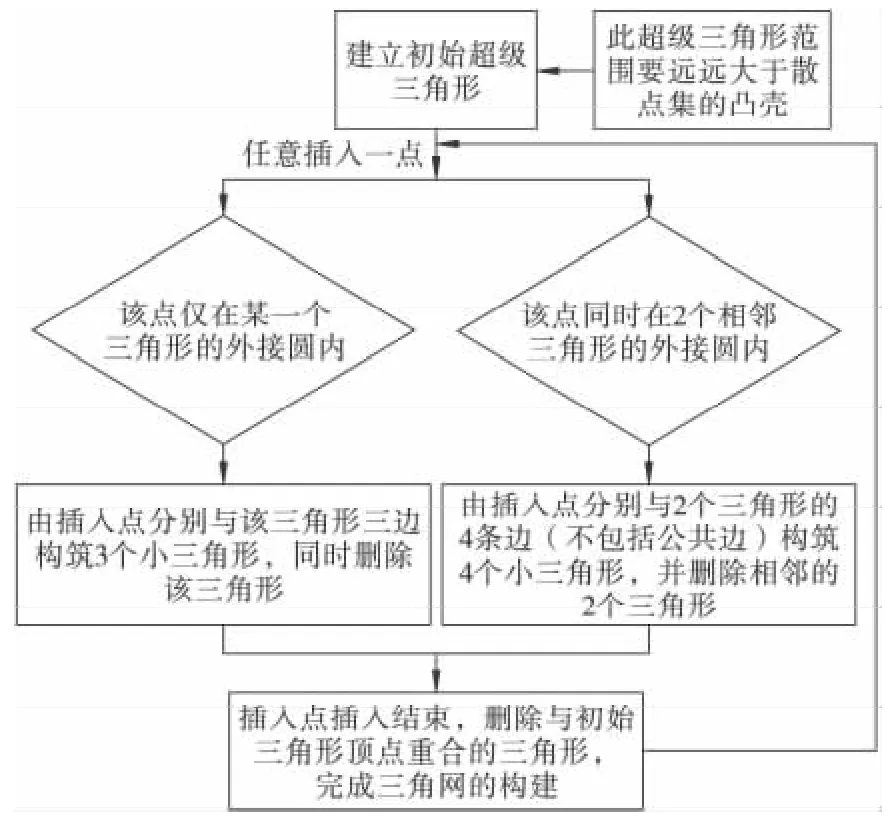
图1 逐点插入法实现步骤Fig.1 Implementation steps of incremental insertion method

露天矿采场现状图、局部挖掘底面图等均由线段集构成，故通常采用带约束的DTM 算法(即所有线段都是三角形的边)进行矿体建模，实现过程见图2。

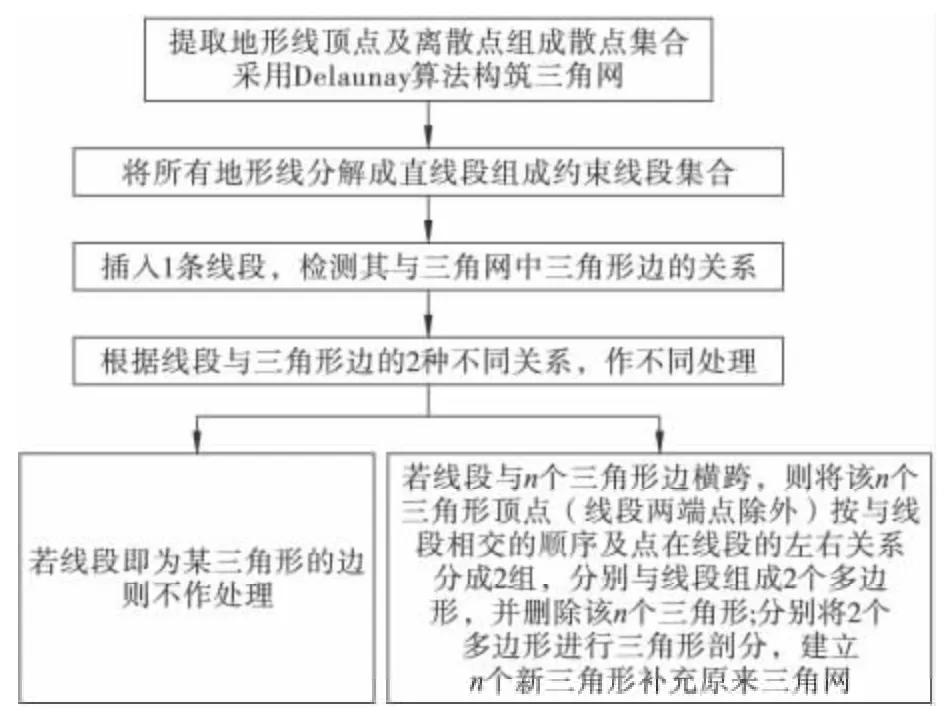
图2 带约束DTM 算法实现步骤Fig.2 Implementation steps of DTM with constraints

由图2 可知，重复第3、4 步，直到检测完成约束线段集合内的所有线段为止，带约束的DTM 便构建完成。若DTM 无法离散为三维块体模型，可将水平面上表示地表空间曲面的三角网离散成规则的矩形(2D Block)，地表空间曲面便表现为很多带有高程点的小矩形构建的曲面，如此便得到了地表空间DTM离散模型。

1.3 模型算法

1.3.1 判断三角面中所包含的2D Block

矿床模型参数确定后，2D Block 中心点即为规则的矩阵数组，3D Face 图元包括1 个边框属性(即GetBoundingBox，MinPoint，MaxPoint)，大大缩小了属性的判断范围，仅需搜索3D Face 的边框内的2D Block，在此基础上进一步判断2D Block 是否在三角形内。由此获得了三角形内所包含的2D Block，并加入判断成功标识，以便在后续判断中无需再参与判断，从而加快了程序的运行速度。

1.3.2 计算2D Block 中心点高程

设2D Block 中心点为O(a，b，c)，所在空间三角形3 个顶点为A(a1，b1，c1)、B(a2，b2，c2)及C(a3，b3，c3)，则三角面的法向量n(i，j，k)为

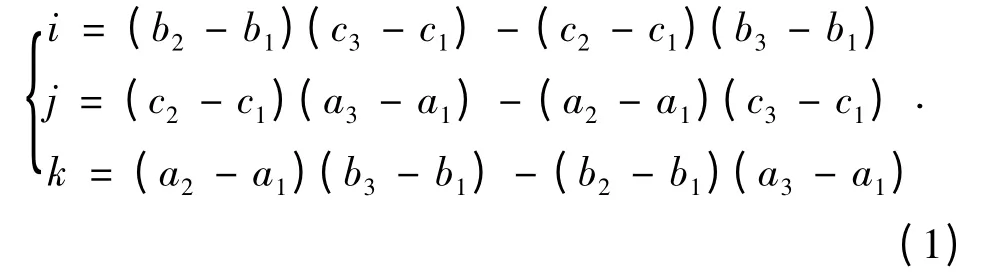
因2D Block 中心点与三角形共面，则有

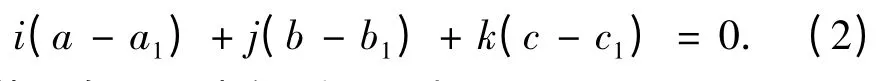
若三角面不为铅垂面，则

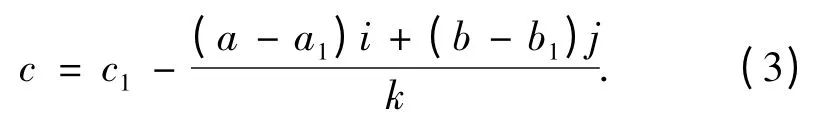
式(3)即为2D Block 中心点高程(c)的计算公式。

1.4 矿岩量计算

首先将建立的采场DTM 离散模型保存在一个二进制文件中，如果某个台阶进行了采剥，则构筑新的采出体的底面，该位置的地表面必然低于原模型中该位置的高程，计算出的各个单元的体积累加量即为挖方量。即若将采场进行了DTM 离散化，其离散化后的每个小矩形对应的高程值为H1，开挖后的地表模型采用相同单元尺寸离散化后的每个小矩形对应的高程值为H2，小矩形块对应体积V2DBlock的计算公式为

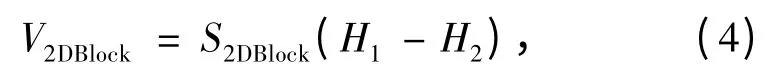
式中，S2DBlock为2D Block 面积，m2。

需要指出的是，采出体的底面必须低于该处的原地形面才为挖方量，即在计算体积时，必须有H1＞H2，如果H1＜H2，则说明该2D Block 为填方。

2 应用实例

2.1 矿山概况

潘家田铁矿是一大型露天钒钛磁铁矿，其年产量600 万t，TFe 品位为23.5%。目前采场最高开采水平为2 220 m，露体底部标高为1 600 m，露天采场底宽35 m，阶段坡面角为65°，台阶高为15 m，生产剥采比为4.50，矿石损失率及贫化率为5%。由于生产过程中采场作业不规范，导致台阶复杂混乱，给测量验收带来了极大困难。

2.2 矿区模型的建立及对比分析

依据采场现状图构建DTM，采用2 m×2 m 单元尺寸进行离散化处理，获得三维DTM 离散模型。依据地质分层图等资料，采用2 m ×2 m 单元尺寸建立三维矿体离散模型。基于已建立的DTM 矿体离散模型，在进行测量验收时，每个离散单元体都有其矿岩区分属性，从而较容易统计出不同矿岩的体积。依据台阶穿孔设计完成采场爆破块段预爆量的计算，依据月末采场局部开挖变化完成采出量的计算，从而形成完整的爆堆台账管理系统。该露天矿山的DTM 离散模型见图3。

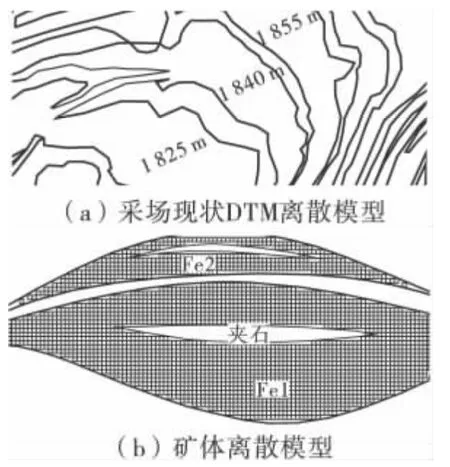
图3 矿山DTM 离散模型Fig.3 DTM discrete model of Open-pit Mine

由图3 可知，DTM 离散模型的可视化效果虽不如三维实体模型，但在计算机建模过程中，DTM 离散模型的运算速度却比三维实体模型快1 个数量级，不会出现运算失败的现象。此外，三维实体模型建模较复杂，闭合实体的过程耗时较长，计算速度较慢，计算不稳定。

采用不同的验收测量方法对爆堆的采出量进行了计算，结果见表1。由表1 可知，相对于其余2 类方法，采用2 m×2 m 单元尺寸建立的DTM 离散模型的计算误差均小于1.00%，因此该模型的计算精度较高。若缩小DTM 离散模型的单元尺寸至1 m ×1 m，计算精度并未得到显著提高，说明2 m×2 m 的单元尺寸已满足要求。

3 结 语

在分析比较矿山原有测量验收方法的基础上，提出了DTM 离散模型法，并分析了模型构建原理及相关算法。将该模型应用于四川潘家田大型露天钒钛磁铁矿的测量验收，结果表明，该方法的计算精度与三维实体模型的误差不到1.00%，计算速度比三维实体模型快1 个数量级，稳定性较高。

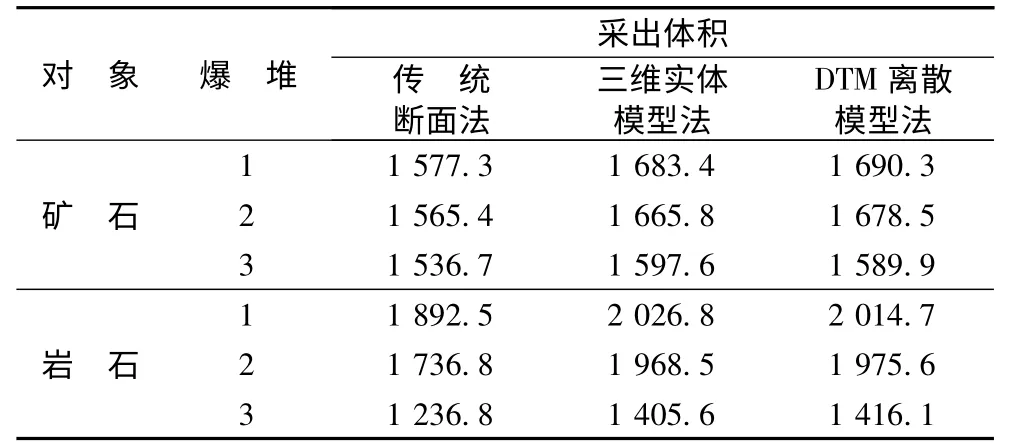
表1 爆堆采出体积计算结果Table 1 Calculation results of muckpiles volume m3

［1］ 韩 亚，王卫星，李 双，等. 基于三维激光扫描技术的矿山滑坡变形趋势评价方法［J］.金属矿山，2014(8):103-107.

Han Ya，Wang Weixing，Li Shuang，et al. An evaluation method of mine landslide and deformation trend based on three-dimensional laser scanning technology［J］.Metal Mine，2014(8):103-107.

［2］ 王新生，马海涛，宁化展. 基于Java 3D 的场地平整土方计算小软件的研究与实现［J］.金属矿山，2013(6):49-52.

Wang Xinsheng，Ma Haitao，Ning Huazhan.Research and realization of small software for calculation of earthwork in site leveling based on Java 3D［J］.Metal Mine，2013(6):49-52.

［3］ 罗德仁，邹自力，汤江龙.工程土方量计算比较分析［J］.东华理工学院学报，2005，28(1):59-64.

Luo Deren，Zou Zili，Tang Jianglong.Contrasting and analysis of the method of earthwork calculation［J］. Journal of East China Institute of Technology，2005，28(1):59-64.

［4］ 高艳磊.基于3DMine 的露天采矿设计［J］.金属矿山，2015(4):255-258.

Gao Yanlei.Design of 3DMine software in open-pit mining［J］.Metal Mine，2015(4):255-258.

［5］ 赵玉国.块体模型算量方法在宝日希勒露天矿中的应用［J］.露天采矿技术，2012，20(6):11-12.

Zhao Yuguo.The application of block model to calculate the amount method in Baorixile open-pit mine［J］. Opencast Mining Technology，2012，20(6):11-12.

［6］ 刘 军，王 鹤，李 峰，等. 露天矿边坡影像三维重建技术［J］.金属矿山，2015(4):259-261.

Liu Jun，Wang He，Li Feng，et al. Image-based 3D reconstruction technology for open-pit slope［J］.Metal Mine，2015(4):259-261.

［7］ 蒲 浩，宋占峰，詹振炎.基于约束Delaunay 三角剖分的道路三维建模方法［J］.华中科技大学学报:自然科学版，2005，33(6):111-113.

Pu Hao，Song Zhanfeng，Zhan Zhenyan. 3D-modelling for roads based on constrained Delaunay triangulation［J］. Journal of Huazhong University of Science ＆ Technology:Natural Science Edition，2005，33(6):111-113.

［8］ 车德福，殷作如，张瑞玺，等. 井巷工程三维建模及无缝开挖模拟技术［J］.煤炭学报，2012，37(4):548-552.

Che Defu，Yin Zuoru，Zhang Ruixi，et al.The method of 3D modeling for tunnel engineering and the simulation technology of its seamless excavating［J］. Journal of China Coal Society，2012，37(4):548-552.

［9］ 李建欣，怀进鹏，李先贤，等. DTM:一种面向网络计算的动态信任管理模型［J］.计算机学报，2009(3):493-505.

Li Jianxin，Huai Jinpeng，Li Xianxian，et al. DTM:a dynamic trust management model for internet computing environments［J］.Chinese Journal of Computers，2009(3):493-505.

［10］ 席靖智.基于DEM 的工程土方计算方法优化分析及应用研究［D］.重庆:重庆交通大学，2013.

Xi Jingzhi. Optimization Analysis and Application Research of Earthwork Calculating Method Based on DEM［D］. Chongqing:Chongqing Jiaotong University，2013.

［11］ 蔡美峰，李角群，杨志军.基于三角形剖分算法建立三维巷道模型的研究［J］.中国矿业，2011，20(5):75-79.

Cai Meifeng，Li Jiaoqun，Yang Zhijun. Study on the 3D-roadway model by the triangulation algorithm［J］. China Mining Magazine，2011，20(5):75-79.

［12］ 顾清华，卢才武，冯治东.空间可视化复杂矿体剖面三角拼接算法研究［J］.金属矿山，2012(6):97-101.

Gu Qinghua，Lu Caiwu，Feng Zhidong.Complex orebody spatial visualization orebody profile triangulation algorithm［J］.Metal Mine，2012(6):97-101.

［13］ 杨 钦，白润才.CAD 二次开发在三维地质建模中的应用［J］.微计算机信息，2010(6):169-170.

Yang Qin，Bai Runcai.The secondary development of CAD and its application in the 3D geological model building［J］.Microcomputer Information，2010(6):169-170.

［14］ 张渭军.孔隙水文地质层三维建模与可视化研究［J］. 金属矿山，2010(8):128-131.

Zhang Weijun.3D modeling and visualization for interstitial geo-hydrology succession［J］.Metal Mine，2010(8):128-131.

［15］ 李 丽.三维空间Delaunay 三角剖分算法的研究及应用［D］.大连:大连海事大学，2010.

Li Li.Study and Application of Three-dimensional Delaunay Triangulation Algorithm［D］. Dalian:Dalian Maritime University，2010.

［16］ 宫世伟.Delaunay 三角剖分方法在三维地形可视化中的应用［D］.鞍山:辽宁科技大学，2011.

Gong Shiwei. Application of Delaunay Triangulation Method in Three-dimensional Terrain Visualization［D］. Anshan:Liaoning University of Science and Technology，2011.

［17］ 蔡美峰，李角群.半连续半离散模型在矿山设计中的应用［J］.北京科技大学学报，2012，34(8):853-858.

Cai Meifeng，Li Jiaoqun. Application of a semi-continuous and semi-discrete model to mine design［J］. Journal of University of Science and Technology Beijing，2012，34(8):853-858.

［18］ 王京卫，丁 宁，赵同龙.场地平整中土石方量计算的三维可视化方法［J］.测绘工程，2006，15(6):15-19.

Wang Jingwei，Ding Ning，Zhao Tonglong.3D-visualization method of earthwork computation in leveling off the construction ground［J］.Engineering of Surveying and Mapping，2006，15(6):15-19.

［19］ 王若慧.基于VBA 的AutoCAD 二次开发及应用实例［J］.计算机应用，2007，26(9):30-33.

Wang Ruohui.The VBA-Based secondary development of AutoCAD［J］.Journal of Computer Applications，2007，26(9):30-33.

［20］ 武 妍. 基于VBA 的AutoCAD 二次开发系统的研究与应用［D］.太原:太原理工大学，2008.

Wu Yan. Research and Application of AutoCAD Second Development System Based on VBA［D］. Taiyuan:Taiyuan University of Technology，2008.