基于地质统计学方法的某铁矿资源量估算
周 旋 王选问 金 瑜
(新疆远山矿产资源勘查有限公司,新疆 乌鲁木齐830011)
地质统计学方法以区域化变量为理论基础,采用变异函数(或称结构函数)拟合样品品位、体重等随机变量的空间变化特征及强度,并对该类数据的分布进行最优无偏内插估计。该方法考虑了区域化变量的结构性及随机性,能够充分利用矿山各类勘探数据及其空间关系,通过模拟信息样品的分布特征,拟合出合理的估值参数,对块体进行最优估值。
随着计算机技术的快速发展,传统资源量估算方法已经难以满足矿山信息三维可视化以及资源储量动态管理的需求[1]。近年来,地质统计学方法及三维可视化技术得到了广泛研究[2],但由于国内外矿业管理体制的差异以及该方法自身的复杂性,导致其并未得到推广应用。本研究以吉尔吉斯斯坦某大型沉积变质型铁矿床为对象,借助储量计算软件建立地质数据库,以此为基础建立矿体三维地质模型及块体模型,并采用克里格法对块体模型进行品位估值[3],估算资源量,通过与距离反比法及传统平行断面法进行对比,分析地质统计学方法的优越性。
1 矿床地质特征
位于吉尔吉斯斯坦纳伦州贾曼套复向斜北翼次级褶皱某向斜核部的某矿床,产于一套以中—酸性火山喷发沉积为主的中深变质的片麻岩类中,为一大型沉积变质型铁矿床。出露的地层主要为下泥盆统奥尔托组第一至第四岩性段,第一岩性段为黑云母片麻岩夹云母石英片岩,第二岩性段为斜长角闪片麻岩,第三岩性段为角闪变粒岩,第四岩性段为黑云母变粒岩。由于受大型断裂活动的影响,形成了一系列分支及次级断裂,各岩性段均为断层关系接触,在矿区北西端发育有与断裂活动相关的细粒石英闪长岩。该矿床共包含17 个矿体,其中18#矿体最大,占资源总量的92.20%;矿体呈似层状、层状及透镜状断续分布,具有分支复合、膨大缩小的现象;矿体总体走向118°,倾向SW,平均倾角为73°,控制矿体长1 850 m,斜深最大达440 m,矿体厚度变化较大,最小5.42 m,最大73.94 m,平均31.50 m;矿床勘查方式为勘探线剖面法,勘探线间距为100 m。多年来共施工探槽33 个、钻孔133 个,系统采集化学样品6 573 件。
2 矿体三维地质建模
2.1 地质数据库
各类地勘数据是矿体三维地质建模的基础,主要包括钻孔(含探槽、硐探等)孔口坐标、测斜、样品测试数据,此外还包括地表地形数据、开采数据及勘探线剖面数据等。在搜集矿区已有的工程数据及其他各类地质地形数据的基础上,利用三维储量计算软件建立地质数据库。该数据库主要包括166 个有效钻孔(或探槽)、169 个小体重样品测试数据以及6 753件化学样品分析结果(分析项目为磁性铁(mFe)品位),其次还包括资源量估算断面图、1 ∶2 000 矿区地形图、1 ∶50 000区域地形图等。上述数据均建立在三维坐标体系之上,每个数据均有其对应的三维空间坐标,实现了地质数据库的三维可视化[4]。
2.2 矿体三维模型
考虑到该矿床的勘查方式,矿体沿走向延伸较长,确定采用剖面法建立矿体三维地质模型[5-6]。首先在三维可视化数据库的基础上绘制勘探线剖面图,按工业指标和地质特征在单个勘探线剖面上进行矿体解译,形成矿体线;然后利用特殊三角网将相邻勘探线的矿体线依次对应连接,形成一个内外不相通的空间实体,即为矿体的三维模型(见图1),其表面由一系列相邻的不规则三角片组成,任意一条三角片的边都为其相邻三角片的公用边[7]。为了更好地与传统储量估算方法进行对比,沿用地质报告所采用的工业指标圈连矿体,即磁性铁(mFe)边界品位为10%,最低工业品位为15%,最低可采厚度为2 m,夹石剔除厚度为2 m。

图1 矿体三维模型Fig.1 3D model of ore-body
3 矿体品位估值
为了形象表征矿体内部品位的变化特征,首先将矿体划分为许多相同规格的小长方体单元,形成块体单元集合体,即块体模型[8];然后结合信息样品分布特征,建立变异函数模型,根据变异函数模型特征值,采用地质统计学方法对离散化的块体单元进行估值,即形成矿体的品位模型[9],用以描绘矿体内部品位信息的分布情况及估算资源量。
3.1 样品组合处理
为了获得品位的无偏、线性估计量,要求信息样品应落在相同的承载之上,即具有相同的权重(样长)。在矿产勘查过程中,样品长度虽有规定值(2 m),但在实际采样过程中,仍不可避免地产生了一定数量样长偏离规定值的样品,故有必要对所有参加品位估值的数据进行等权化处理,将品位信息通过样长加权的方法量化到若干空间离散点上。对矿区6 573件化学样品的样长进行统计,其中有5 226 件共79%以上的样品的样长为1.5 ~2.5 m。为了尽可能保持数据的原有特征,确定按2 m 的组合长度对样品进行等长处理。
通过对全区信息样品的磁性铁(mFe)品位进行统计,得到磁性铁(mFe)品位的分布特征,见图2。
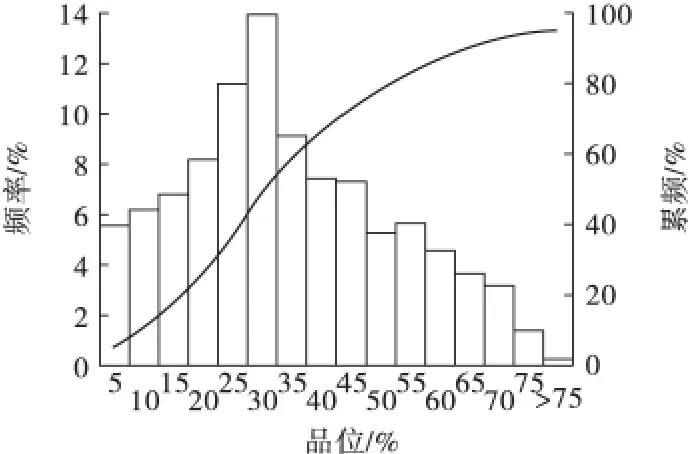
图2 磁性铁(mFe)品位分布直方图Fig.2 The histogram of mFe grade distribution
由图2 可知,磁性铁(mFe)品位的平均值为31.85%,标准差为26.51%,变化系数为0.83,品位分布基本具有正态分布特征,适宜选用地质统计学法进行统计估值。
3.2 变异函数及结构分析
变异函数(变差函数)考虑了变量值之间及其与所处空间位置的相关性,能够真实反映样品品位值在矿体内的区域变化规律。受样品品位的离散性限制,变异函数往往无法直接求取[10],需要借助试验变异函数选取某种理论模型,并对试验变异函数曲线进行拟合[11]。在地质勘探和采矿实践中多以球状模型或指数模型来拟合试验变异函数曲线,确定变异函数模型特征值,为块体模型估值。为此,选用球状模型拟合试验变异函数曲线,由于矿体中品位分布具有各向异性特征,不同方向的变异函数具有不同的变程,样品的实际影响范围为一椭球体,称之为各向异性椭球体[12]。沿矿体走向(主轴)、延伸(次轴)、厚度(短轴)3 个方向的球状模型变异函数拟合曲线如图3 所示。

图3 球状模型变异函数拟合曲线Fig.3 Fitting curves of variation function of spherical model
由图3 可知,矿石磁性铁品位在3 个方向上表现出明显的各向异性,其变异函数有较好的结构性,说明矿体中信息样品的分布具有区域化变量特征,适合采用地质统计学方法进行品位估值和资源量估算。各方向上变异函数的特征值见表1。

表1 变异函数特征值Table 1 Characteristics value of variation function
3.3 创建块体模型
充分考虑到矿体中元素品位的变化特征,将矿体划分成若干个尺寸相等的长方体块体,每个块体都有其对应的质心点,块体所有的属性(包括空间位置、体积、体重、品位、矿石类型等)都可集中于其质心点上,因此也称块体单元为点元[13]。此处的“块体”与常规资源量计算方法中的“块段”意义相近,但它充分考虑了矿体中品位的变化特征,采用了无偏的、最小误差的数理统计法对矿体的品位分布进行插值,因而估值结果更接近实际情况,可有效克服传统块段法品位估值的缺点。
块体模型中,单元块尺寸主要取决于矿体的类型、规模、开采方式等,为了使得块体模型更逼近于矿体形态,矿体边缘需分割为比单元块更小的块体,称为次级块。块体尺寸对估值的结果有十分重要的影响,一般来说,块体越大,所有块体的估值结果越趋于平均,越反映不出矿体内品位随空间的变化关系,也体现不出块体的优越性;反之,块体尺寸过小,估值结果变化不大,反而增加计算量。
铁矿的基本勘探线距为100 m,现行开采方式为露天开采,开采基本台阶高12 m,结合变异函数特征,基本单元块体尺寸确定为10 m×10 m×10 m,次级单元块体尺寸为5 m×5 m×5 m,整个矿体模型共划分为14 908 个单元块。
3.4 品位估值
采用地质统计学方法分析矿体中信息样品的分布特征及变化规律,并对块体模型进行估值,利用球状模型拟合试验变异函数曲线,确定理论变异函数和搜索椭球体参数,选用克里格法进行品位估值。克里格法的实质是通过建立并求解克里格方程组,为每个信息样品值给出一个权值,利用加权平均法以最小的估计方差求出块体线性无偏估计品位[14-15]。该方法搜索椭球体参数由信息样品分布形态主轴方向的变异函数及品位信息各向异性特征所决定,主轴搜索半径理论上应为矿体主轴方向变异函数的变程[16],但在实际勘查过程中,时有出现探矿工程分布不均匀的情况,导致部分块体搜索不到足够的信息样品,此时,可适当增大主轴搜索半径,确保每个块体都能够完成估值。本研究采用的搜索椭球体参数见表2,通过对块体模型进行品位估值,形成的品位模型见图4。
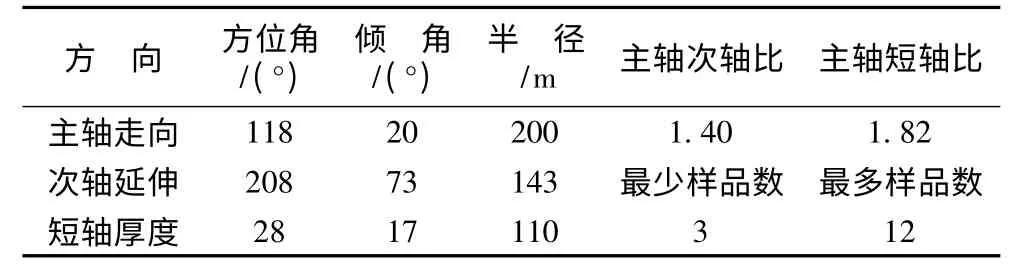
表2 搜素椭球体参数Table 2 Parameters of search ellipsoid

图4 品位磁性铁(mFe)品位模型Fig.4 Grade model of mFe
4 资源量估算
4.1 估算方法
4.1.1 传统估算方法
传统的资源量估算方法主要为几何法,该方法以勘探线及探矿工程为依据,将矿体划分为若干个小块段,利用与块段有关的工程资料,确定该块段的几何形态及计算参数来估算资源量。该方法一般以二维平面图件为基础,并将块段形态抽象为规则几何体,难以准确表现矿体复杂的三维形态;计算参数采用算数平均法或简单加权平均法求取,未能充分利用空间变量的相关性,当工程分布不均匀,厚度、品位及体重变化大时,误差很大;此外,块段的体积一般都比较大,品位、体重过于平均,无法准确反映矿体品位的各向异性特征。该方法也有其独特的优势,具有简单易懂、容易理解并掌握的特点,在工程控制程度低、获取地质数据少时或对估算精度要求不高时,可以利用该方法快速估算资源量。
4.1.2 地质统计学方法
地质统计学方法以区域化变量为理论基础,以变异函数为基本工具,以克里格法为估值方法,充分考虑到矿体中各信息样品间及信息样品与待估块之间的空间相关性,因而估值结果更符合矿山自然规律[17-18]。计算过程为建立数据库—矿体三维建模—变异函数模拟(搜索椭球体)—块体模型—品位模型—汇总资源量[19]。该方法实现了资源量计算的自动化、智能化,提高了计算效率,便于实现资源储量的动态管理[20]。该方法建立在对大量信息样品统计的基础上,因此适宜在勘探程度高或已投入生产的矿山使用,而在勘探程度低、样品数据少时,难以采用数学模型来拟合信息样品的空间分布形态,因而该方法优势不明显。
4.1.3 对比分析
上述2 类资源量估算方法特点对比见表3。由表3 可知,地质统计学方法与传统几何方法各有所长,但地质统计学法有其独具的科学性及合理性,在估值过程中,充分考虑了矿体中品位分布的随机性及自相关性,有效弥补了常规几何方法的不足。
4.2 资源量估算结果
本研究选用了距离反比法和常规平行断面法估算资源量,以便对克里格法进行验证,结果见表4。
由表4 可知,克里格法和距离反比法均属地质统计学方法,两者估值原理略有不同,估值结果略有差异,而矿体体积同为矿体三维模型实际体积,因此,估算结果差异不大。克里格法与平行断面法(传统估算方法)相差较大,约相差8%,其中平均品位、密度及体积均有所差异。造成这种误差的原因主要为2类估算方法求取计算参数的途径不同,且其精度也有所差别。地质统计学方法所采用的体积为每个块体的实际体积,在对品位进行估值时,不仅考虑了各信息样品相对于块体的空间位置,而且考虑了有限区域内其他信息样品间的相互空间关系,因此估值精度较高。平行断面法以勘探线为基础划分块段,块段形态经过规则化近似处理,块段厚度、品位的计算以控制该块段的各单工程为依据,采用算数平均法或简单加权平均法求取,该方法法忽略了矿体品位的空间变化特征,对空间变量过于平均,估值误差较大。

表3 传统几何法与地质统计学方法对比Table 3 Comparison between traditional geometric method and geostatistics method
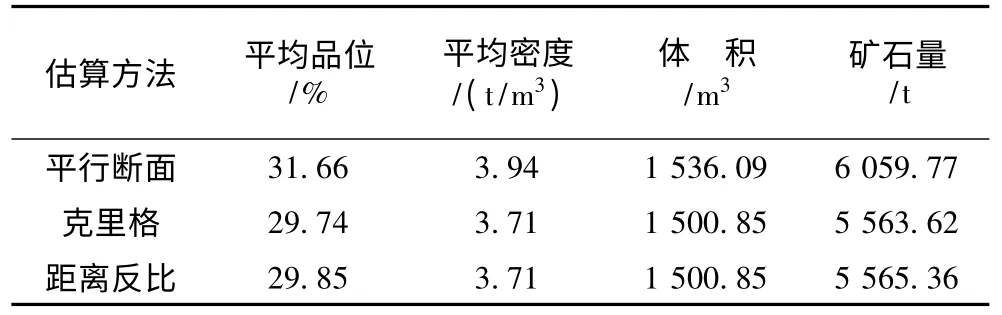
表4 几类方法资源量估算结果比较Table 4 Comparison between different methods of reserves estimation
5 结 语
基于地质统计学理论,借助储量计算软件建立矿体三维模型,合理划分块体单元,并利用克里格法对品位的分布进行插值,完成资源量估算。相对于传统的资源量估算方法,该算法充分考虑到矿体品位的空间分布特征,合理划分计算单元,能够最大限度地利用地勘数据,估值精度较高。总体来看,该方法适合于勘探程度高、地勘数据量大的金属矿床,当勘探程度低、数据量小时,该方法的优势得不到发挥,此时,可以根据矿体形态、勘探方式等实际情况选用合理的传统几何方法估算资源量。
[1] 张渭军.基于四面体的地质体可视化与剖分研究[J]金属矿山,2011(1):85-88.
Zhang Weijun.Visualization and incision of geo-body based on tetrahedral network[J]. Metal Mine,2011(1):85-88.
[2] 肖 斌,赵鹏大,侯景儒. 地质统计学新进展[J]. 地球科学进展,2000,15(3):293-296.
Xiao Bin,Zhao Pengda,Hou Jingru.New development of geostatistics[J].Advance in Earth Sciences,2000,15(3):293-296.
[3] 潘 懋,方 裕,屈红刚.三维地质建模若干基本问题探讨[J].地理与地理信息科学,2007,23(3):1-5.
Pan Mao,Fang Yu,Qu Honggang.Discussion on several foundational issues in three-dimensional geological modeling[J]. Geography and Geo-Information Science,2007,23(3):1-5.
[4] 龚元翔,王李管,冯兴隆,等. 三维可视化建模技术在某铜矿中的应用[J].矿冶工程,2008,28(3):1-4.
Gong Yuanxiang,Wang Liguan,Feng Xinglong,et al. Application of 3-D visualization modeling technique in a copper mine[J]. Mining and Metallurgical Engineering,2008,28(3):1-4.
[5] 陈国旭,田宜平,刘 刚,等.资源储量估算、图表编制一体化与可视化系统研究[J].金属矿山,2009(4):102-105.
Chen Guoxu,Tian Yiping,Liu Gang,et al. Study on the integrated and visualization system of mineral reserves estimation,tabling and mapping[J].Metal Mine,2009(4):102-105.
[6] 邹艳红,戴塔根,毛先成.广西大厂矿田铜坑深部隐伏矿体立体定量预测建模与可视化研究[J].地质与勘探,2008,44(2):62-66.
Zou Yanhong,Dai Tagen,Mao Xiancheng. Three-dimensional grid quantitative prognos is modeling and visualization for concealed ore bodies in depths of Tongkeng,Dachang mining area[J]. Geology and Exploration,2008,44(2)62-66.
[7] 余海军,李文昌,尹光候,等. 三维地质模型的开发及应用——以普朗铜矿为例[J].现代矿业,2009(6):67-71.
Yu Haijun,Li Wenchang,Yin Guanghou,et al.Development and application of three-dimensional geological model:taking Pulang copper deposite for example[J]. Morden Mining,2009 (6):67-71.
[8] 朱青凌,罗周全,刘晓明,等. 块体模型储量估算原理的应用研究[J].矿冶工程,2012,32(6):9-13.
Zhu Qingling,Luo Zhouquan,Liu Xiaoming,et al. Applicable research of reserves estimation theory with the block model[J].Mining and Metallurgical Engineering,2012,32(6):9-13.
[9] 陈爱兵,秦德先,张学书,等.基于MICROMINE 矿床三维立体模型的应用[J].地质与勘探,2004,40(5):77-80.
Chen Aibing,Qin Dexian,Zhang Xueshu,et al.3D Model for deposit based on MICROMINE technology[J]. Geology and Exploration,2004,40(5):77-80.
[10] 曾怀恩,黄声享,杨保岑,等. 变异函数理论模型的参数估计[J].测绘信息与工程,2007,32(3):31-33.
Zeng Huaien,Huang Shengxiang,Yang Baocen,et al.Parameter estimation of variogram theory model[J]. Journal of Geomatics,2007,32(3):31-33.
[11] 黄诗峰,金菊良,段进军,等.地质统计学中变差函数参数估计的新方法[J].地质与勘探,1999,35(1):41-43.
Huang Shifeng,Jin Juliang,Duan Jinjun,et al. A new method for estimating variogram parameters in Geostatistics[J]. Geology and Exploration,1999,35 (1):41-43.
[12] 房智恒,王李管,冯兴隆,等.基于地质统计学的矿山储量估算[J].矿业快报,2008(10):28-31.
Fang Zhiheng,Wang Liguan,Feng Xinglong,et al. Mine reserves estimation based on Geostatistics[J].Express Information of Mining Industry,2008(10):28-31.
[13] 孙玉建,孟 伟,万 会.矿产资源储量估算中工程控制程度划分的探索[J].地质与勘探,2006,42(6):81-84.
Sun Yujian,Meng Wei,Wan Hui.A new method for classifying degree of engineering controlling in resources and reserves estimation[J].Geology and Exploration,2006,42(6):81-84.
[14] 邢红星,琚太忠,林建阳.普通克里格法在矿产储量计算中的应用[J].地质与勘探,1997,33(4):46-51.
Xing Hongxing,Ju Taizhong,Ling Jianyang.The ordinary Kriging's application to mineral calculation of reserves[J].Geology and Exploration,1997,33(4):46-51.
[15] 杨建宇,秦德先,康泽宁,等. 地质统计学在北衙金矿的应用[J].矿业研究与开发,2006,26(2):14-17.
Yang Jianyu,Qin Dexian,Kang Zening,et al. The application of Geostatistics in Beiya gold mine[J]. Mining Research and Development,2006,26(2):14-17.
[16] 李章林,张夏林.距离平方反比法矿产资源储量计算模块设计与实现[J].地质与勘探,2007,43(6):92-97.
Li Zhanglin,Zhang Xialin.Designing and realization of mineral resources reserve calculation module using inverse distance square method[J].Geology and Exploration,2007,43(6):92-97.
[17] 冯兴隆,李 德,李剡兵,等.最优估值方法在DIMINE 软件中的实现及应用[J].中国钼业,2011,35(2):13-16.
Feng Xinglong,Li De,Li Yanbing,et al.Implement and application of optimal valuation methods in the DIMINE software[J]. China Molybdenumin Dustry,2011,35(2):13-16.
[18] 王炯辉,李 毅,黄冬梅,等.基于普通克里格法的泥河铁矿床资源储量估算研究[J].地质与勘探,2013,49(6):1108-1113.
Wang Jionghui,Li Yi,Huang Dongmei,et al.Reserve estimation of Nihe iron deposit in Anhui Province based on ordinary Kriging methed[J].Geology and Exploration,2013,49(6):1108-1113.
[19] 罗周全,张 保,刘晓明,等.矿体品位和储量统计分析的三维可视化方法[J].有色金属:矿山部分,2008,60(5):23-27.
Luo Zhouquan,Zhang Bao,Liu Xiaoming,et al. 3D visualization method of analysis and estimation of orebody grade and reserves[J]. Nonferrous Metals:Mining Section,2008,60(5):23-27.
[20] 侯景儒,黄竞先.地质统计学在固体矿产资源/储量分类中的应用[J].地质与勘探,2001,37(6):61-66.
Hou Jingru,Huang Jingxian.Application of geostatistics in classification for resources/reserves of solid fuels and mineral commodities[J].Geology and Exploration,2001,37(6):61-66.

