一种条带状铜多金属矿储量估算插值方法

李怀良 庹先国， 蒋 鑫

(1.核废物与环境安全国防重点学科实验室，绵阳 四川621010;2.地质灾害防治与地质环境保护国家重点实验室，成都 四川610059)

西藏墨竹工卡县甲玛矽卡岩－角岩型铜多金属矿床是我国目前同类矿床中矿石品质最好、成矿元素最多、探明的资源量已经达到超大型规模的矿床［1］。目前，一般采用传统断面法、SD 法和普通克里格法［2-3］估算该地区的矿床储量。传统断面法虽然具有一些不足，但经过几十年的发展，在矿产资源储量估算方面已日趋完善，只要合理选取地质参数，不但能够简化计算，而且能够达到较高的精度［4-5］。近年来，SD 法在我国发展也十分迅速，北京恩地科技发展有限责任公司开发的SD 法矿产资源储量计算系统已通过国土资源部组织的评审鉴定，该系统可广泛应用于西藏甲玛铜多金属矿的矿床勘查至开采完成各个阶段的储量计算。普通克里格法的优势也较为明显，不但能够给出储量估算的精度，而且是无偏且估计方差最优的［6-9］。

西藏甲玛铜多金属矿区内地层复杂，地层曲面变化较大，甚至可能存在地层曲面相交和错断的现象，因此钻孔数据常呈条带状分布［10-14］，并且多种金属间会出现协同区域化以及多种金属储量分布相互影响的现象，因此有必要消除多种金属的相关性以及条带状效应造成的钻孔两端数据权值偏大的影响［15-17］。为此，采用权值校正［18］的协同克里格法对协同克里格法插值得到的权值进行校正，在估值方差基本不变的前提下使得协同克里格法估值的权值更为合理。

1 协同克里格法

采用协同克里格法［6-10，19-20］进行储量估算时，对由K 个变量构成的协同区域化变量{Zk(x)}(k = 1，2，3，…，K)，有相邻m 个位于位置ui(i = 1，2，3，…，m)处的数据点，其中心点的品位数据设为Z(uk，i)(i= 1，2，3，…，m;k = 1，2，3，…，K)，在待估点Z(u0)处的协同克里格的估计量为

式中，λk，i为第k 个区域化变量中的第i 个样本点的权值，由最小化方差求出，即

设样品数据点ui(i = 1，2，3，…，m)与待估点u0的距离为di，对于式(1)中的权值，如果di＜dj，则λk，i＞λk，j(i，j = 1，2，3，…，m)，且有

该算法主要实现流程见图1。

2 钻孔条带状效应

西藏甲玛铜多金属矿最主要的数据有地面钻孔数据、钻孔化验数据、小体重数据等。原始数据为截至2012 年甲玛矿区勘探工程数据，包括58 个钻孔共15 187 件样品的数据。若某个钻孔遇到断层，钻孔数据便会出现边界截断现象，如图2 所示。

如图3 所示，在进行协同克里格插值时首先需要确定一个搜索范围，搜索范围在三维空间内通常为一个椭球体的边界截断。图1、图2 所示的2 类数据可称为钻孔的有限条带状数据。

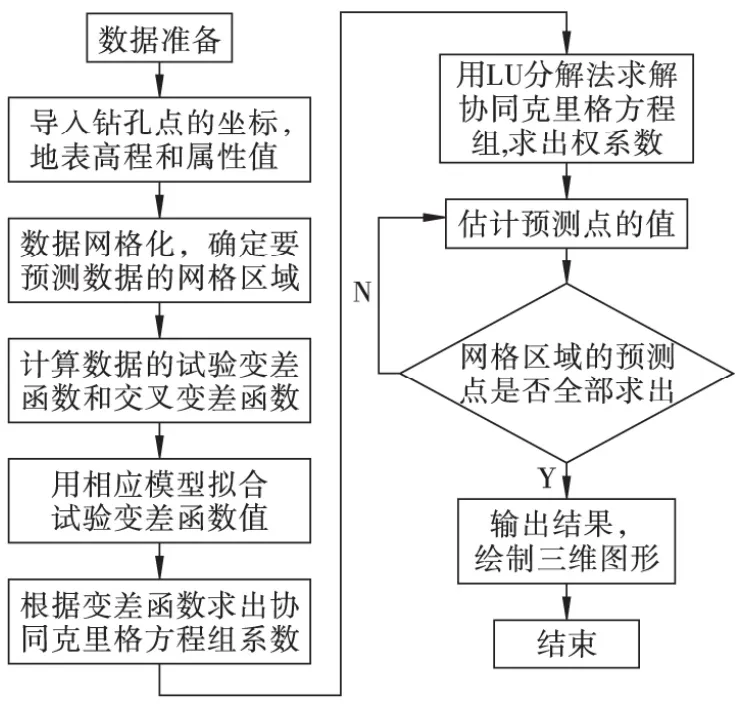
图1 协同克立格法实现流程Fig.1 Implementation process of Co-Kriging interpolation algorithm

图2 数据被断层边界截断Fig.2 Drilling data truncated by boundary faults

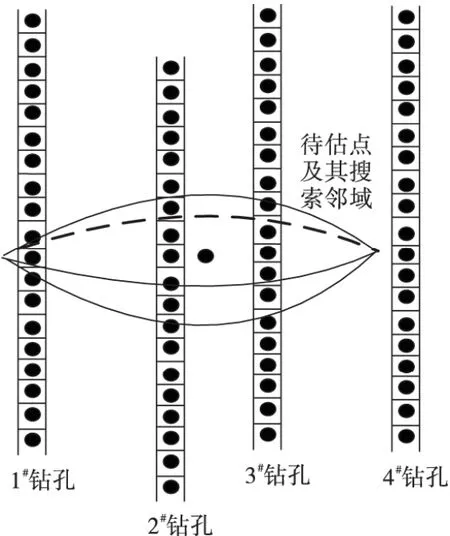
图3 数据被搜索邻域截断Fig.3 Drilling data truncated by search field

以Cu 和Ag 的协同区域化为例，对其中的一列有限的条带状数据进行协同克里格插值计算，其中变差函数以及2 种元素的交叉变差函数均采用球状模型计算。其中Cu 块金效应为0 的协同克里格权值如图4 所示。

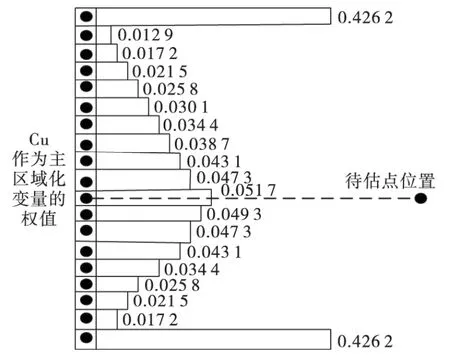
图4 协同克里格插值引起的条带状效应Fig.4 Banned effect caused by Co-Kriging interpolation

图4 显示的权值体现了采用协同克里格法估值时所产生的条带状效应，对于单个钻孔数据的估值，与待估点距离最远的钻孔数据两端样品点的权值偏大，反之则普遍较小。根据克里格估值法中的屏蔽效应［13-16］，该图中计算的权值是不符合实际情况的，特别当钻孔数据分布于断层中或搜索范围截出不平稳的钻孔数据时，便会出现端点数据处的权值明显大于或小于中间数据权值的现象，因此有必要对其进行校正。

3 权值校正

对权值系数进行约束需满足式(3)中的最小化问题约束条件。采用拟牛顿法［11］对权值进行校正，流程见图5。

图5 拟牛顿法校正权值流程Fig.5 Flow of weight correction by Quasi-Newton method

4 处理结果

4.1 数据预处理

采用权值校正协同克里格法估计矿床储量时，应首先选取区域化变量。区域化变量必须具备随机性和结构性的双重性质，由于西藏墨竹工卡县甲玛夕卡岩－角岩型铜多金属矿床为Cu、Mo、Au、Ag、Pb、Zn 等复合多金属矿床，并有大量的钻孔化验数据，因此可选取金属元素的品位作为区域化变量，本研究采用Cu 品位进行分析。在矿产储量和品位计算之前，对钻孔数据进行预处理，包括特异值处理与样品组合处理。根据Cu 品位数据，在正态概率纸上绘制累积频率曲线图见图6。

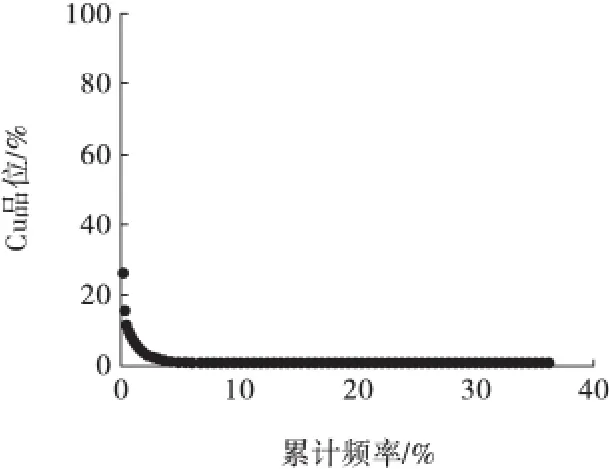
图6 Cu 品位累积频率曲线Fig.6 Cumulative frequency curve of Cu grade

由图6 可知，Cu 品位累积频率曲线基本符合正态分布。在直线上部存在少量离散点，且偏离直线，该类离散点为真正的特异值。此次估算采用频率曲线法将所有高于上截品位的数据全部用上截品位值代替。取1.5% 为上截品位值，矿区Cu 品位高于1.5%的共有782 件样品。上截品位代替前、后Cu 特异值统计分析结果见表1。

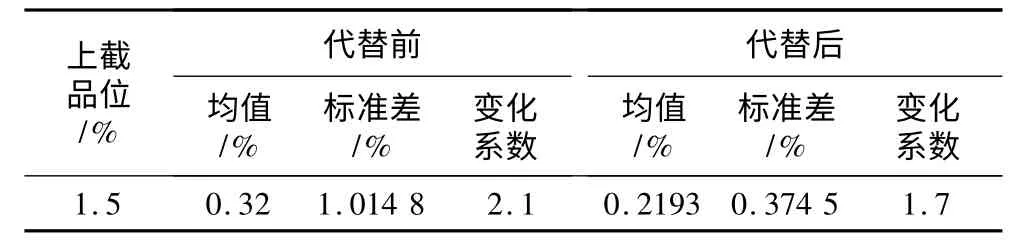
表1 Cu 特异值处理结果Table 1 Results of singular value of Cu

采用权值校正协同克里格法估算资源量时，组合样品长度设定为6 m。组合样品中Cu 品位特征值的统计结果见表2。

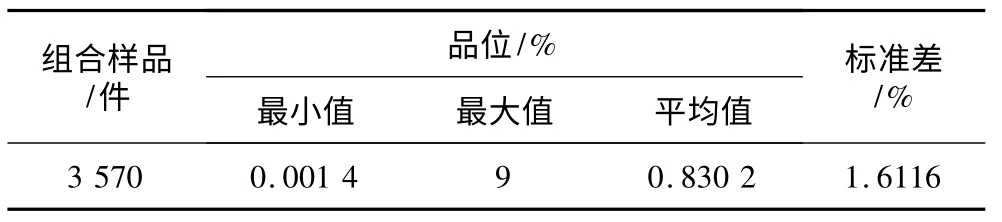
表2 组合样品中Cu 品位特征值Table 2 Statistical results of Cu grade characteristic values of composite samples

4.2 协同克里格法估算储量

4.2.1 变差函数及结构分析

对组合样品进行统计分析，结果见表3。由表3可知，组合样品中Cu 品位与Ag 品位相关性最大，因此以Ag 品位作为辅助变量对Cu 的品位进行估值。

权值校正协同克里格法插值的第一步是得到Cu、Ag品位的变差函数及两者的交叉变差函数。首先将所有钻孔点两两组合成点对，计算出其距离值;然后以球状模型拟合成理论试验变差函数曲线。Cu、Ag 品位项的3 个变差函数轴的方向定位及其计算结果见表4。

表3 组合样本统计分析Table 3 Composite samples analysis results

表4 Cu 和Ag 变差函数参数Table 4 Variation function Parameters of Cu and Ag

由表4 可知，2 种元素在各个方向上的变差函数参数相似，所有变差函数均为各向同性的。对Cu、Ag品位项的3 个轴方向上的变差函数进行结构套合，得到Cu、Ag 品位的变差函数模型

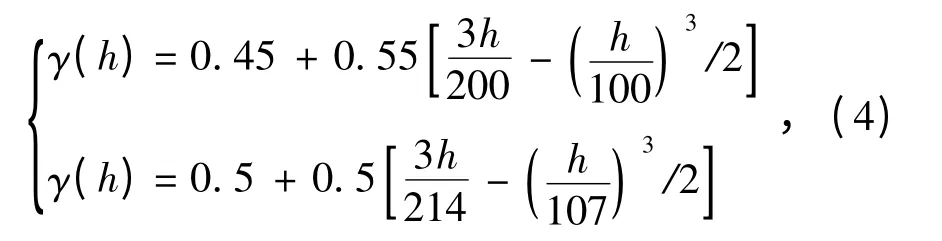
式中，h 为滞后距，m。

以上述2 种元素品位为基础，用球状模型拟合计算出交叉变差函数的基台值为0.58 m，拱高为0.42 m，变程为55 m，其交叉变差函数曲线见图7。

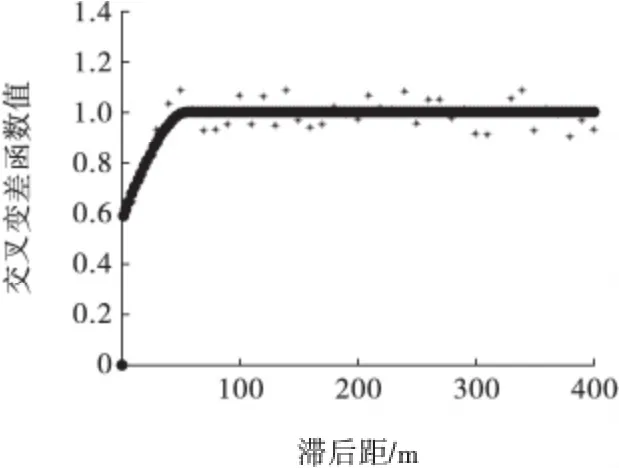
图7 交叉变差函数曲线Fig.7 Cross-variogram function curve

4.2.2 权值校正

选取钻孔编号为2012jm－8576 的条带状数据为测试数据，选取钻孔中间位置为待估位置，求解协同克里格方程组得到的权重系数，按图5 所示的拟牛顿法进行权值校正，单个钻孔校正后的权值见图8。

图8 权值校正结果Fig.8 Results of weight calibration

由图8 可知，待估样品点位于197#样品点附近，距离待估点附近的权值偏大，反之则权值越小，符合实际情况。

4.2.3 算法模型验证

对甲玛矿区化学样品中Cu 品位估值情况进行交叉验证，结果见图9。协同克里格插值模型与权值校正协同克里格模型的交叉验证结果见表5。

图9 交叉验证结果Fig.9 Results of interactive verification

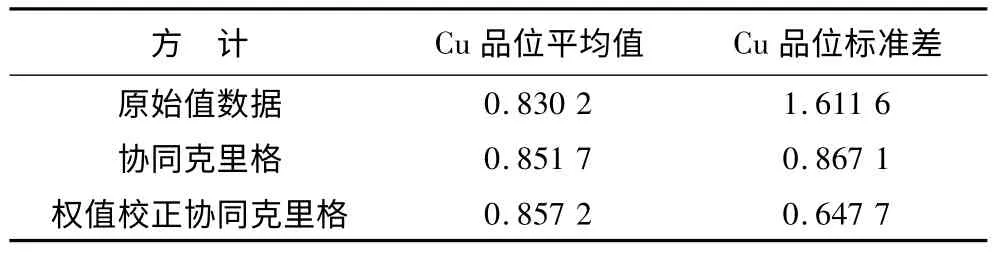
表5 2 种插值模型交叉验证结果Table 5 Interactive verification results of two interpolation models %

经交叉验证，残差值大体呈正态分布，各元素品位实际值与估计值的误差趋于0，表明模型合理。同时，相对于普通协同克里格模型而言，在3 570 个组合样品点上，权值校正协同克里格插值模型降低了估值的平均误差，且其标准差相对较小，表明该模型储量估算精度具有优势。

4.2.4 储量估算

针对三维块段模型的储量计算，首先考虑甲玛矿区的勘探网度和变差函数的特征，确定单元块段的尺寸等参数如表6 所示。

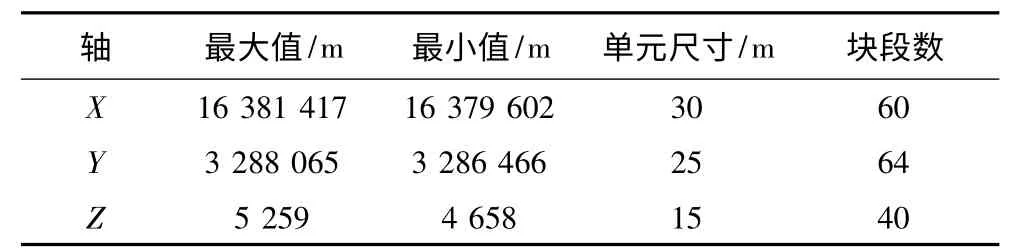
表6 块段估值参数Table 6 Valuation parameters of block segment

甲玛矿区总共划分出153 600 个单元块段，对每个单元块段的Cu 品位进行估值时，应首先确定待估点的搜索范围。由于Cu 品位的变差函数模型以及与辅助变量之间的交叉变差函数模型均呈球状模型变化趋势，因此采用权值校正协同克里格法进行估值时，搜索范围可定义为如图10 所示三维椭球体，综合考虑Cu 品位球状模型参数和矿区钻孔分布间隔等因素，分别取三维椭球体长轴为200 m，次轴为200 m，短轴为30 m。经计算，甲玛矿区共探获夕卡岩型矿体中铜金属量约209 万t(含伴生铜金属量约28 万t)，基本符合实际情况。

图10 搜索范围Fig.10 Search field

5 结 语

依据西藏甲码铜多金属矿的钻孔数据资料，在对原始钻孔数据进行预处理的基础上，通过计算Cu、Ag的变差函数及其交叉变差函数，构造协同克里格方程组，求解得到权值。采用拟牛顿法对不符合实际情况的权值进行校正，并对西藏甲玛矿区的Cu 储量进行了估算，估算结果与实际情况基本一致，可为矿山开采设计提供依据。

［1］ 黎枫佶.西藏墨竹工卡县甲玛铜多金属矿三维模型构建和资源量估算［D］.成都:成都理工大学，2010.

Li Fengji.Constructing 3D Models and Estimating Reserves of Jiama Copper Polymetallic Deposit，Mozhugongka County，Tibet［D］.Chengdu:Chengdu University of Technology，2010.

［2］ 余牛奔，齐文涛，王立欢，等.基于3DMine 软件的三维地质建模及储量估算——以新疆巴里坤矿区某井田为例［J］.金属矿山，2015(3):138-141.

Yu Niuben，Qi Wentao，Wang Lihuan，et al. Three-dimensional geological modeling and reserve estimation based on 3DMine software:taking a well field of Balikun mining area，Xinjiang as an example［J］.Metal Mine，2015(3):138-141.

［3］ 程 勖. 地质统计学软件开发与应用［D］. 长春:吉林大学，2009.

Cheng Xu. Development and Application of Geostatisties Software［D］.Changchun:Jilin University，2009.

［4］ 唐 攀，唐菊兴，唐晓倩，等. 传统方法和地质统计学在矿产资源储量分类中的对比分析［J］.金属矿山，2013(11):107-109.

Tang Pan，Tang Juxing，Tang Xiaoqian，et al. The comparative research of traditional method and geostatistics method in mineral resource/reserve classification［J］.Metal Mine，2013(11):107-109.

［5］ 余 璨，李 峰，张达兵，等.基于DMINE 的红龙厂铜矿床地质建模与储量计算［J］.金属矿山，2015(2):108-111.

Yu Can，Li Feng，Zhang Dabing，et al.Geological modeling and calculation of the reserves of Honglongchang copper deposit based on DIMINE［J］.Metal Mine，2015(2):108-111.

［6］ 李庆谋.多维分形克里格方法［J］.地球科学进展，2005，20(2):248-256.

Li Qingmou. Multi-fractal Krige interpolation method［J］. Advances in Earth Science，2005，20(2):248-256.

［7］ 肖克炎，张晓华，王全明，等. 应用改进的克里格法分离重力区域异常与局部异常［J］.物探化探计算技术，1995，17(2):19-25.

Xiao Keyan，Zhang Xiaohua，Wang Quanming et al.Separation of regional field and local field by improved Kriging method［J］.Computing Techniques for Geophysical and Geochemical Exploration，1995，17(2):19-25.

［8］ 高美娟，朱庆忠，张淑华. 利用贝叶斯－克里金估计技术进行储层参数预测［J］.石油地球物理勘探，1999，34(4):390-397.

Gao Meijuan，Zhu Qingzhong，Zhang Shuhua. Reservoir parameter prediction using Bayes-Kriging estimation technique［J］. Oil Geophyical Prospecting，1999，34(4):390-397.

［9］ 李 君，李少华，毛 平，等. Kriging 插值中条件数据点个数的选择［J］.断块油气田，2010，17(3):277-279.

Li Jun，Li Shaohua，Mao Ping et al. Choosing the number of conditional data in Kriging interpolation［J］.Fault-Block Oil ＆ Gas Feild 2010，17(3):277-279.

［10］ 汪 保，孙 秦.改进的Kriging 模型的可靠度计算［J］.计算机仿真，2011，28(2):113-116.

Wang Bao，Sun Qin. Structural reliability computation based on Kriging model［J］.Computer Simulation，2011，28(2):113-116.

［11］ 孙 卡，翁正平，李章林，等.排序扫描线算法在克里格估值中的应用［J］.金属矿山，2009(7):73-76.

Sun Ka，Weng Zhengping，Li Zhanglin，et al.Application of sequential scanning algorithm in Kriging prediction［J］.Metal Mine，2009(7):73-76.

［12］ 牛文杰，朱大培，陈其明. 滑动领域克里金插值法的改进［J］.计算机辅助设计与图形学学报，2001，13(8):752-756.

Niu Wenjie，Zhu Dapei，Chen Qiming. Improvement of moving neighborhood Kriging method［J］. Journal of Computer-Aided Design ＆ Compute Graphics，2001，13(8):752-756.

［13］ 李少华，王勇标，李 君，等. 克里金估值中条带效应的校正［J］.石油地球物理勘探，2012，47(6):979-983.

Li Shaohua，Wang Yongbiao，Li Jun，et al. Correcting the string effect of Kriging［J］. Oil Geophyical Prospecting，2012，47(6):979-983.

［14］ 牛文杰，孟宪海，李吉刚.结合软数据的同位置协同克里金估值新方法［J］.煤田地质与勘探，2011，39(2):13-17.

Niu Wenjie，Meng Xianhai，Li Jigang. A new estimation method of collocated Co-Kring combined with soft data［J］. Coal Geology ＆Exploration，2011，39(2):13-17.

［15］ 侯景儒，黄竞先.地质统计学的理论与方法［M］.北京:地质出版社，1990.

Hou Jingru，Huang Jingxian. Theory and Method of Geostatistics［M］.Beijing:Geological Publishing House，1990.

［16］ 孙仁铎.空间变异理论及其应用［M］.北京:科学出版社，2005.

Sun Renduo.Spatial Variability Theory and Application［M］. Beijing:Science Press，2005.

［17］ 孙红泉，康永尚，杜惠芝.实用地质统计学程序集［M］.北京:地质出版社，1997.

Sun Hongquan，Kang Yongshang，Du Huizhi. Utility of Geostatistical Procedures Set［M］. Beijing:Geological Publishing House，1997.

［18］ 易君君，汪 保，颜倩倩.基于新拟牛顿方程的优化算法设计及应用［J］.宁波工程学院学报，2015，27(1):12-18.

Yi Junjun，Wang Bao，Yan Qianqian.Design and application of optimization algorithm based on new Quasi-Newton equation［J］.Journal of Ningbo University of Technology，2015，27(1):12-18.

［19］ 王小朋，刘翔峰.一种基于病态问题的修正牛顿法［J］.河南科技大学学报:自然科学版，2015，36(1):86-91.

Wang Xiaopeng，Liu Xiangfeng. A modified Newton method based on ill-conditioning problem［J］.Journal of Henan University of Science and Technology:Natural Science，2015，36(1):86-91.

［20］ 张华军，赵 金，罗 慧.基于拟牛顿法的同时扰动随机逼近算法［J］.华中科技大学学报:自然科学版，2014，42(9):1-4.

Zhang Huajun，Zhao Jin，Luo Hui. Simultaneous perturbation stochastic approximation algorithm based on Quasi-Newton method［J］.Journal of Huazhong University of Science ＆ Technology:Natural Science Edition，2014，42(9):1-4.