地应力对岩体爆破影响的数值模拟

张凤鹏 彭建宇 张 鑫 李元辉

(1.深部金属矿山安全开采教育部重点实验室，辽宁 沈阳110819;2.山东省黄金工程建设监理中心，山东 烟台264002)

随着人们对能源需求量的增加和矿山开采强度的不断增大，浅部资源日益减少，国内外多矿山相继进入深部资源的开采状态。深部岩体处于较高的地应力环境中，在深部岩体中进行开采爆破时，岩体处于高地应力和爆炸冲击波的共同作用，两种载荷相互影响，导致岩体爆破破坏过程比较复杂。目前，高应力条件下岩石的爆破日益受到国内外学者的重视［1-3］，国内外学者从实验、理论分析和数值模拟等方面对高应力深部岩体爆破过程进行研究。肖正学等［4］通过对存在不同初始应力场的几种材料的室内试验，认为初始应力场的存在可改变爆轰波的传播规律以及对裂纹发展起着导向作用。谢源［5］对高应力条件下岩石爆破裂纹扩展规律的模拟进行了试验研究，研究表明介质爆破裂纹的方向及大小与附加的主应力有关。白羽等［6］研究了地应力对双孔爆破的影响。戴俊等［7］以柱装药爆破漏斗理论为基础，对高地应力巷道崩落爆破标准漏斗形成进行研究。刘艳等［8］通过隐式—显式连续求解进行了地应力作用下岩体爆炸的数值模拟。

尽管国内外学者对高应力条件下岩石爆破进行了大量研究，但多局限在定性分析层面上，相关定量研究成果比较少。本研究将采用ANSYS/LS －DYNA对不同地应力条件下岩石爆破破坏特征进行数值模拟，研究破坏区范围和静应力之间的定量关系。

1 计算模型

1.1 炸药爆炸状态方程

本研究模拟高能炸药在花岗岩中的爆破过程。炸药起爆后，体积膨胀，炸药单元体内一点的压力采用JWL 状态方程模拟:

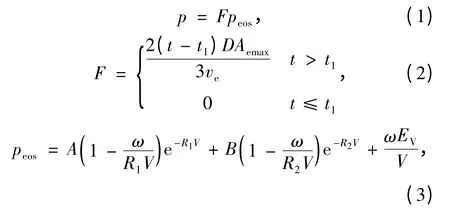
式中，p 为爆炸压力，Pa;F 为炸药化学能释放率;peos为炸药的爆轰压，Pa;D 为炸药爆速，m/s;Aemax和ve分别为炸药最大横截面积和体积;t，t1分别为当前时间和炸药内一点的起爆时间，s;V 为相对体积;EV为内能参数，Pa;A、B、R1、R2、ω 为常数。具体炸药参数见表1。

表1 炸药的材料参数Table 1 Material parameters of explosive

1.2 岩体材料模型

本研究采用双线性随动硬化模型(* MAT_PLASTIC_KINEMATIC)作为岩体的弹塑性屈服模型，屈服应力σY与应变率的关系为

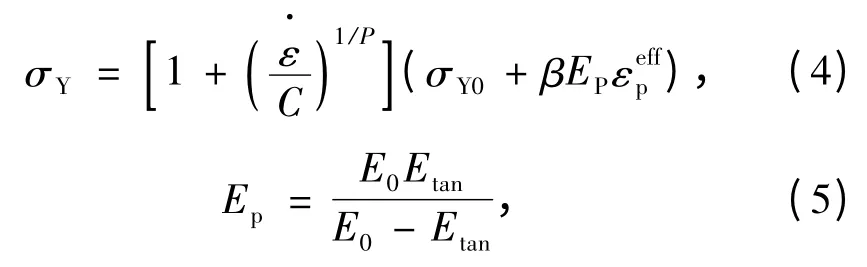
式中，σY0为初始屈服应力，Pa;为应变率，s－1;C 和P 为Cowper －Symonds 应变率参数，取C =2.5 和P=4.0;β 为硬化参数，0 ≤β ≤1 ;EP为塑性硬化模量，Pa;E0为杨氏模量，Pa;Etan为切线模量，Pa;为岩体有效塑性应变，

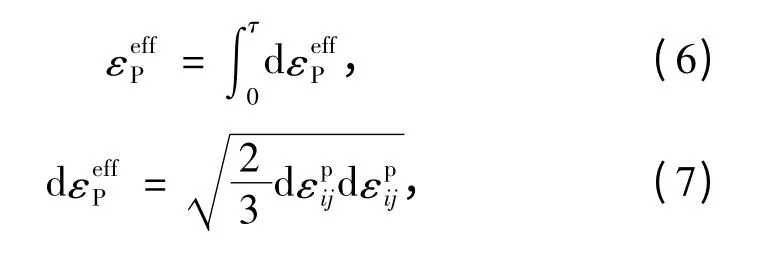
爆破过程中粉碎区采用Mises 屈服破坏准则，而裂纹区采用拉伸破坏准则［9］:

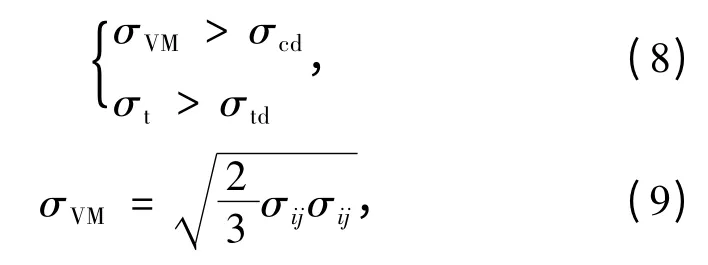
式中，σVM为岩体中任一点的Mises 有效应力，Pa;σt为爆破产生的拉应力，Pa;σcd和σtd分别为岩体的单轴动态抗压强度和抗拉强度，Pa，与静态强度的关系近似取为

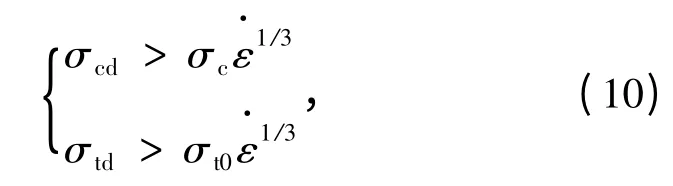
其中σc和σt0分别为岩体的单轴静态抗压强度和抗拉强度。

以花岗岩为研究对象，其弹塑性力学参数见表2。

表2 花岗岩弹塑性力学参数Table 2 Elastoplastic mechanical parameters of granite

2 数值计算与分析

2.1 数值计算模型

本研究模拟柱状药包在无限大岩体内的爆破过程，简化为平面应变问题进行分析。模拟中取炮孔直径d=38 mm，计算模型尺寸为2 m ×2 m，炸药位于模型的几何中心，所建立的计算模型如图1 所示。由于该模型只是无限岩体的一部分，出现了人为的边界，为了消除人为边界处的反射波对结构动力响应的影响，在模型四周边界添加无反射边界条件，以模拟无限岩体。

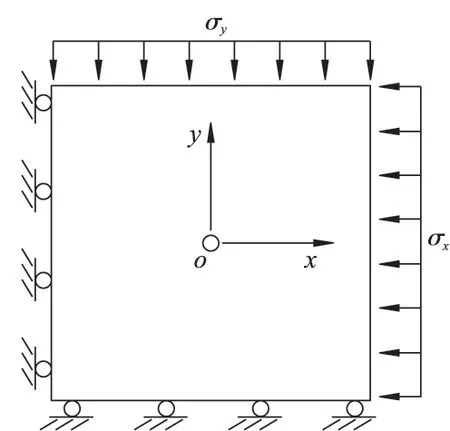
图1 几何模型Fig.1 The geometric model

2.2 初始应力场的加载方案

在ANSYS 中进行隐式分析形成初始应力场，为了对比分析不同附加初始应力情况下岩体爆破特征，设计表3 所列数值分析方案。

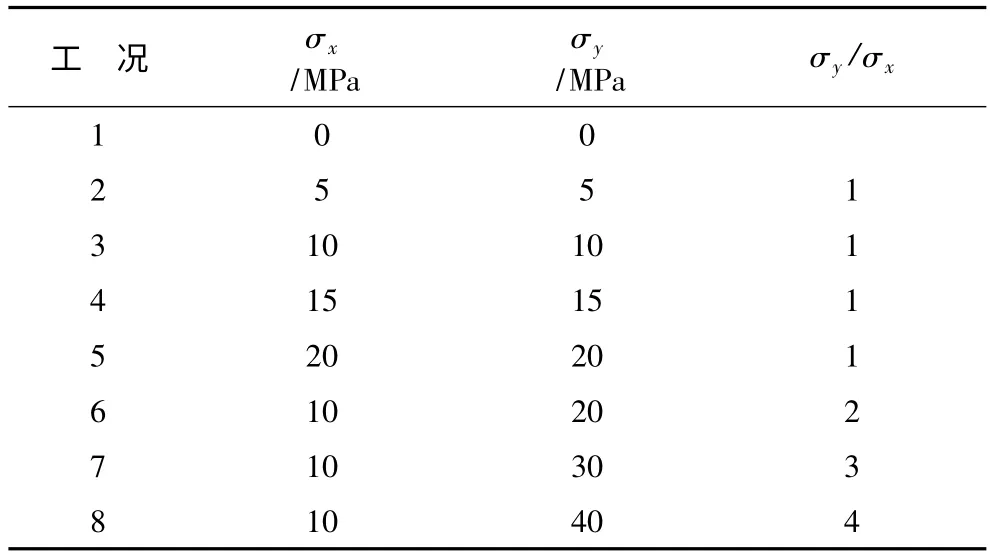
表3 地应力工况Table 3 In-situ stresses field

2.3 计算结果及分析

2.3.1 双向等压地应力场对岩体爆破影响

图2 给出了采用等值双向加载时不同地应力下的裂纹分布，可见:当地应力由0 增加到20 MPa 时，粉碎区的形状没有变化，面积略有减小，但变化不显著。而裂纹在粉碎区外以装药中心为圆心呈放射状分布，裂纹破坏区域为圆形，面积随地应力增大明显减小。因此，本研究重点讨论地应力对裂纹扩展的影响。

图2 双向等值地应力作用下的裂纹分布Fig.2 Cracks distribution under equal bi-directional in-situ stresses

表4 列出了不同地应力下裂纹区直径L 的具体结果。可见:随着地应力增大，裂纹扩展直径减小，由地应力为0 MPa 时的52.6d 减小到20 MPa 时的22.1d，但分布规律基本相同。由于裂纹区以环向拉伸破坏为主，随着与爆腔距离的增加，环向拉应力逐渐减小，此时压地应力抑制了该区域裂纹的扩展，导致裂纹区面积减小，裂纹密度增加，使该区域岩体破碎更充分，而裂纹区外岩体更完整，减小了爆破损伤区范围。

图3 给出了裂纹区面积随地应力变化的规律，其中纵轴A 为每种工况下裂纹区的面积，A = πL2/4 ，采用炮孔横截面积A0进行无量纲化，A0= πd2/4 ;横轴为地应力，σ = σx= σy，采用岩石的抗拉强度σt0(见表2)进行无量纲化。可见，随着地应力增加，裂纹区的面积减小速度明显放缓，有逐渐收敛的趋势。

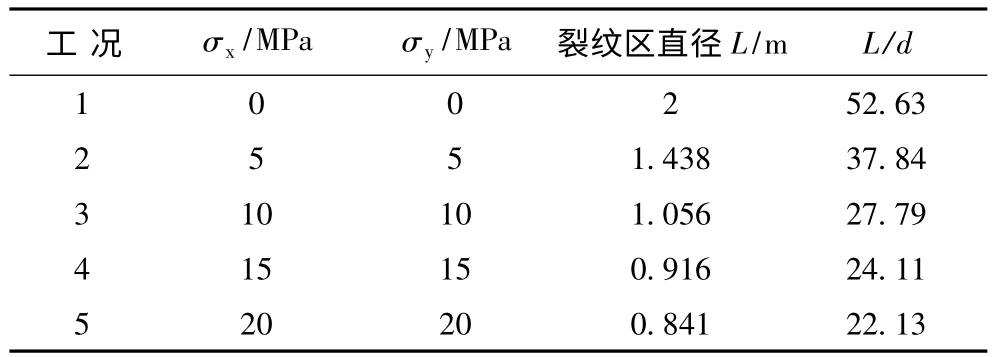
表4 双向等值初始应力下裂纹区范围Table 4 Crack zone under equal bi-directional initial stresses

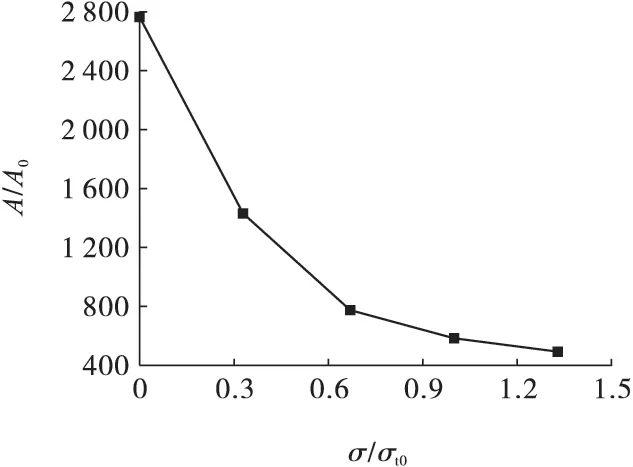
图3 裂纹区面积随地应力变化曲线Fig.3 Variation curve of the area of crack zone with in-situ stresses

将图3 中曲线拟合为

也就是说，对于研究的花岗岩，在使用前述炸药爆破时，裂纹区面积与地应力存在式(11)的量化关系。当地应力不断增大时，裂纹区面积收敛到402.2 倍炮孔横截面积，裂纹区半径约为20 倍炮孔半径。

2.3.2 双向不等压地应力对岩体爆破影响

实际工程中，通常垂直炮孔平面内的2 个主应力是不等的，为此，本研究进一步探讨双向不等压地应力对爆破破岩效果的影响。图4 给出了σx=10 MPa情况下，σy分别取4 种工况10、20、30 和40 MPa 时的裂纹分布。结果表明:在双向不等压地应力作用下，不但裂纹区面积发生变化，形状也发生明显改变，由等压时的圆形转化为不等压工况下的近似椭圆形，长轴出现在较大压应力作用方向，长度为La，短轴出现在较小压应力作用方向，长度为Lb，随较大压应力增加，长轴先增大后减小，短轴减小(见图5)，表明最大压应力方向是破岩的主导方向。

图6 给出了裂纹区面积随较大主应力的变化规律，图中A= πLaLb/4 。可见在双向不等压地应力作用下，裂纹区面积变化过程比较复杂，在一个主应力不变的情况下，随另一主应力增加而先增加，后减小，呈非单调变化。

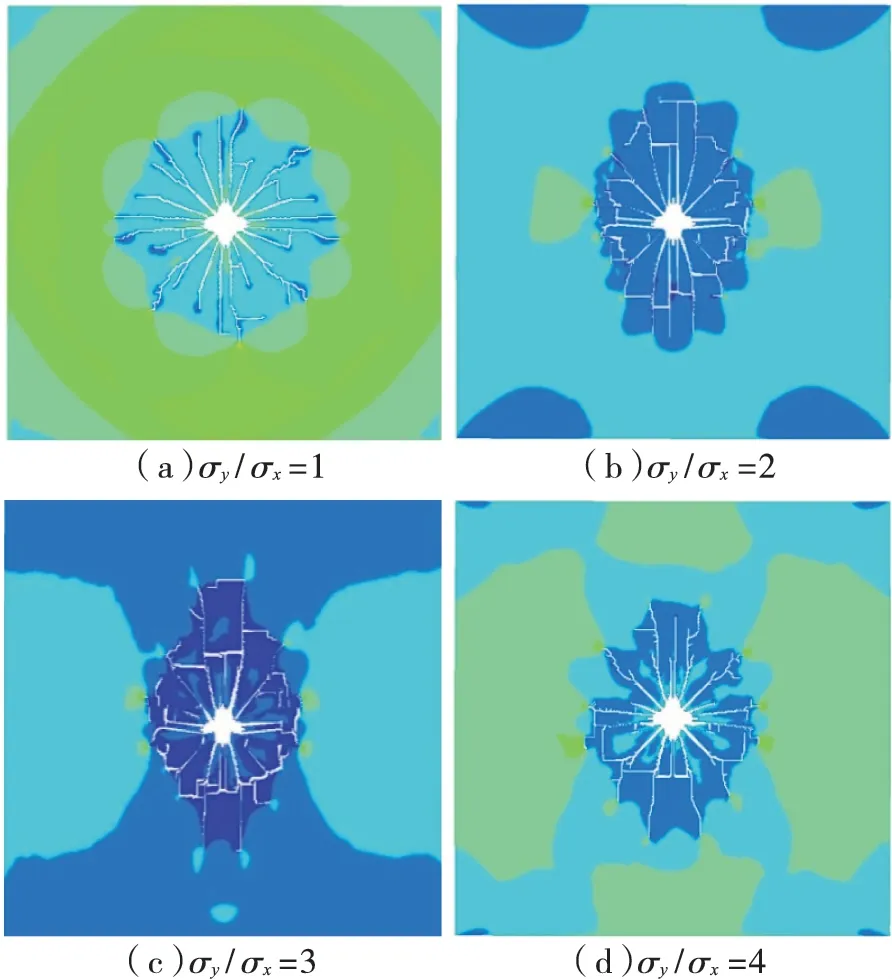
图4 双向不等压工况下裂纹分布Fig.4 Fracture distribution under unequal bi-directional in-situ stresses

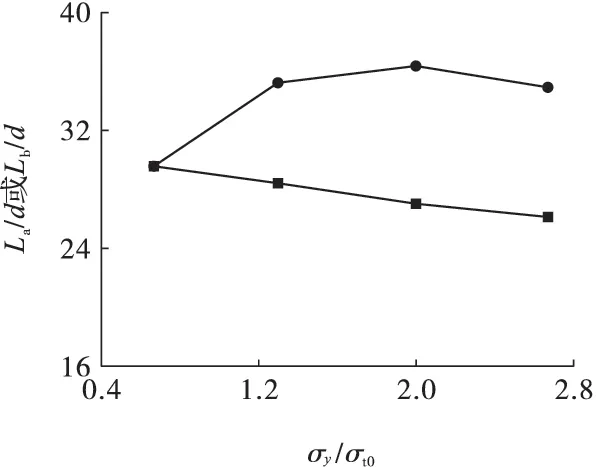
图5 裂纹区长短轴随地应力的变化曲线Fig.5 Variation curve of long axis (short axis)of crack zone with in-situ stresses

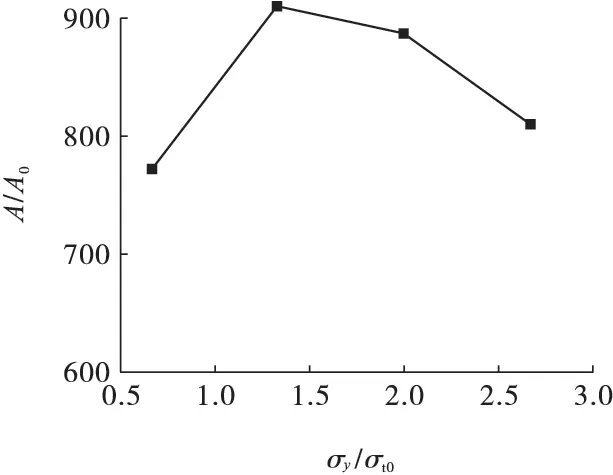
图6 裂纹区面积随地应力的变化曲线Fig.6 Variation curve of the area of crack zone with in-situ stresses

3 结 论

(1)双向等压下，裂纹区形状为圆形，其面积随地应力增大而减小，但裂纹密度增大。对于无限大花岗岩岩体内柱状药包爆破问题，垂直药柱平面内岩体破坏区面积与压应力之间的定量关系为

(2)双向不等压情况下，裂纹区形状为近似椭圆形，长轴出现在较大压应力作用方向，短轴出现在较小压应力作用方向，在较小压应力不变的情况下，随较大压应力增加，长轴先增大后减小，短轴单调减小，裂纹区面积先增加，后减小，最大压应力方向是岩体主破裂方向。

(3)地应力使爆破裂纹分布更集中，局部裂纹密度增大，使该区域岩体破碎更充分，而裂纹区外岩体更完整，减小了爆破损伤区范围。

［1］ Feng X T，Hudson J. Rock Engineering Design［M］. Leiden:CRC Press/Balkema，2011.

［2］ Petr Konicek，Kamil Soucek，Lubomir Stas，et al.Long-hole destress blasting for rockburst control during deep underground coal mining［J］. International Journal of Rock Mechanics ＆ Mining Sciences，2013，61(7):141-153.

［3］ Diering D H.Tunnels under pressure in an ultra-deep Witwatersrand gold mine［J］. The Journal of the South African Institute of Mining and Metallurgy，2000，100(9):319-324.

［4］ 肖正学，张志呈，李端明.初始应力场对爆破效果的影响［J］.煤炭学报，1996，21(5):497-501.

Xiao Zhengxue，Zhang Zhicheng，Li Duanming.The influence of initial stress field on blasting［J］.Journal of China Coal Society，1996，21(5):497-501.

［5］ 谢 源.高应力条件下岩石爆破裂纹扩展规律的模拟研究［J］.湖南有色金属，2002，18(8):1-3.

Xie Yuan.Modelling research of the law on crack extension by blasting in rock with high stress［J］.Hunan's Journal of Nonferrous Metal，2002，18(8):1-3.

［6］ 白 羽，朱万成，魏晨慧，等. 不同地应力条件下双孔爆破的数值模拟［J］.岩土力学，2013，34(S1):466-471.

Bai Yu，Zhu Wancheng，Wei Chenhui，et al.Numerical simulation on two-hole blasting under different in-situ stress conditions［J］. Rock and Soil Mechanics，2013，34(S1):466-471.

［7］ 戴 俊，钱七虎.高地应力条件下的巷道崩落爆破参数［J］，爆炸与冲击，2007，27(3):272-277.

Dai Jun，Qian Qihu.Break blasting parameters for driving a roadway in rock with high residual stress［J］. Explosion and Shock Wave，2007，27(3):272-277.

［8］ 刘 艳，许金余.地应力场下岩体爆体的数值模拟［J］. 岩土力学，2007，28(11):2485-2488.

Liu Yan，Xu Jinyu. Numerical simulation of explosion in rock mass underground stress field［J］. Rock and Soil Mechanics，2007，28(11):2485-2488.

［9］ 夏 祥，李海波，李俊如，等. 岩体爆生裂纹的数值模拟［J］. 岩土力学，2006，27(11):1987-1991.

Xia Xiang，Li Haibo，Li Junru，et al. Numerical simulation of blastinduced cracks in rock［J］. Rock and Soil Mechanics，2006，27(11):1987-1991.