基于对偶拓扑结构的路网路段重要性评估方法

张喜平，李永树，刘 刚

（1．西南交通大学 地球科学与环境工程学院，四川 成都610031；2．重庆邮电大学 软件学院，重庆400065）

现实的复杂路网是非同质的拓扑结构［1］，这一特征决定复杂路网的路段的重要性是各不相同的。对路网中路段节点的重要性评估不仅是研究复杂路网结构与功能的基础性工作，也是交通规划与控制活动的基础［2］。快速、准确地发掘路网中的重要路段不仅能在路网的规划设计中避免因为这些节点的瘫痪给交通造成大面积的拥堵，还能为级联动力学等路网结构之上的功能性研究提供准确的数据支撑。因此，对复杂路网的路段节点重要性的研究已经成为复杂路网研究的重要课题。

现有的复杂路网的路段重要性的研究主要有：Michael［3］等提出一种基于路段选择概率的路段重要性评估方法，该方法在考虑出行者对出行时间的感知误差的前提下，利用算法求出各个路段的选择概率，选择概率越大，路段越重要。这是一种从路段所承担的交通量的角度来评估路段重要性的方法，这种方法在计算路段的选择概率需要路段的实际交通流量，这种数据难以收集。王晓丽等 在其综述性的文献中提到了瑞典的学者Erik Jenal us等人提出的一种路段重要性评估算法，该方法是在路网中，假设路段上已发生使路段降级甚至失效的事件，对路段失效后的后果进行计算，从而根据其确定路段的重要性。这种评估方法把路网的“破坏性等价于重要性”。侯立文等［5］提出一种基于路段可靠性评价的方法用于确定路网中路段的相对重要性评估，这是一种与文献［4］中提到的方法相反的方法。刘思峰等［6－8］利用网络的连通性来反映路网中路段节点的重要性，这是利用图论的方法对路段重要性进行评估。在一定程度上，路段节点自身的度、介数等属性反映了路段的重要程度，但这并不能准确地刻画路段在整个路网中的重要度，路段的重要性还跟相邻路段及其他较远路段的重要性密切相关。因此，认为路段的重要度是路网上所有路段共同作用、贡献的结果。

基于这种考虑，引入m阶邻居节点的概念，提出一种基于对偶拓扑的复杂路网路段重要度评价方法，建立具有普适性的评价模型。该方法考虑了路段自身属性及m阶邻居节点的属性对路段重要度的贡献，以度、介数为考察参数，建立同时顾及度值和介数值的评估模型，与传统的度值法、介数法等评估方法相比，本文方法能更有效地评估复杂路网路段的重要度并确定路网中的关键节点与关键路径。

1 复杂路网路段重要度评估方法

1．1 理论基础

定义1 路网对偶图［9－11］。建立基于 GIS路网拓扑的对偶图，对偶拓扑方法是将道路按道路名称映射为节点，交叉口映射为边。

定义2 节点度值是指节点直接相连边的数量，记为D。目前普遍认为节点的度值可以直接反映节点的重要程度。节点的度值越高，则说明该节点越重要。

定义3 m阶邻居节点。对于复杂网络G＝｛V， L ｝中任意节点i（i∈V），其1阶邻居节点为与节点i之间距离为1的节点，该类节点构成的集合称作节点i的1阶邻居节点集，记为π（1）（i）；同理，则与节点i之间距离为2的节点为2阶邻居节点，其构成的集合称作节点i的2阶邻居节点集，记为π（2）（i）；如此类推，则与节点i之间距离为m 的节点称为m阶邻居节点，其构成的集合称作节点i的m 阶邻居节点集，记为π（m）（i）。

1．2 路段节点重要度评估方法

在现实生活中对目标对象重要性进行评估时，通常会综合考虑多方面因素的影响。对于网络节点而言，其重要性并不是完全取决于节点的度、介数或其他特性，需要同时顾及这些因素，才能对节点的重要性做出较为准确的评估。这里，假设针对每个节点选取n个评价指标，用δi，j表示节点i的第j个指标值。由此，可以定义节点i的重要度评价模型［12］：

式中：Ii为节点i的重要度；A为评估系数矩阵或重要度贡献矩阵，用于表示节点自身及各阶邻居节点对节点i重要性的贡献程度，且认为同阶邻居节点对节点i具有相等的贡献程度，即其评估系数相等；Ei为节点i的评估指标矩阵，包含节点i及各阶邻居节点的指标值；W 为指标权重矩阵，用于表示节点i的重要性对各类指标的依赖程度，这里将n个评价指标所占权重分别记为ω1，ω2，…，ωn。对于多因子情况，保留单因子评价函数中同阶邻居节点对节点i重要度贡献的计算方法，即

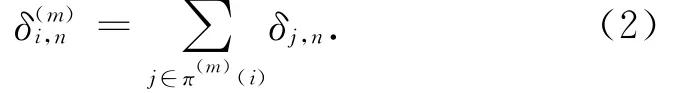
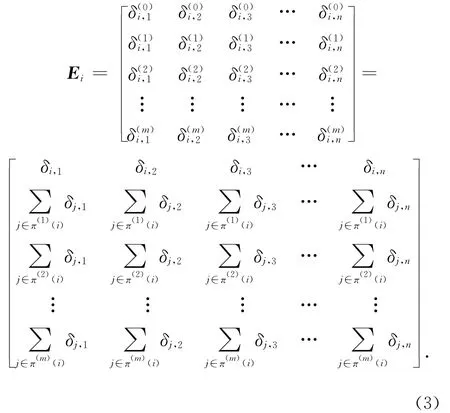
由于不同指标的取值范围可能相差很大，例如同一节点的度为几十，而其介数可能达到几千。各指标的物理意义和计量单位不一定相同，导致数据的量纲和数量级可能不同。所以，需要对评估指标矩阵Ei做归一化处理。由式（1）可知，其中每列元素对应一个指标，总共有n个指标。对Ei中的每一个指标值采用式（4）。

式中：δ′（k）i，j为归一化后的指标值，由δ′（k）i，j可以计算出归一化评估 指 标 矩 阵 E′i。令 A ＝ ［α，γ，γ2，…，γm］，W ＝ ［ω1，ω2，ω3，…，ωn］T，由此网络中任意节点i的重要度Ii＝A·E′i·W ，即

式中，指标权重矩阵n个指标集合的取值为1，并且每一个ωj大于等于0，α和γ为两个参数，其用于调节节点重要度评估对节点自身特性及m阶邻居节点的依赖程度。m为邻居节点的深度。

1．3 算法流程

考虑到路段节点本身及其m阶邻居节点在各类指标约束下对节点的重要度贡献，可以得到较为精确的评价结果。路段节点在对偶拓扑中的度与介数等指标可以反映路段节点的重要程度。已知GIS复杂路网，所考察邻居节点深度m，根据上述多因素的评估模型，给出评估节点重要度的具体算法：

1）从GIS路网结构图映射出对偶拓扑结构：G＝｛V ，L｝ 。V是路网的顶点集合，也是路网的路段集合。L是路网边的集合，也是路网的交叉路口的集合；

2）根据对偶拓扑结构，提取任意路段节点i＝1，2，…，m 阶邻居节点集：π（1）（i），π（2）（i），…，π（m）（i）；

3）计算路段节点i的各阶邻居节点集的每个指标值：

4）针对Ei中每类指标做归一化处理，计算归一化后的评估指标矩阵E′i；

5）根据式（5）计算每个路段节点的重要度，输出Ii。

得到每个路段节点的重要度后，将所有路段节点按照重要度值从大到小进行排序。这样，重要度取值越大的节点就越为重要。根据节点重要度的降序排列结果，可以确定路网中最为重要的路段节点或关键路段节点集。

2 试验与仿真

为了验证本文的评估方法，选用成都市道路网的GIS图作为真实网络的验证。根据文献［11］的方法，首先将成都市路网GIS图转换成对偶模型，然后利用式（1）的评估模型选取度和介数两大计算因素计算对偶模型中路段节点的重要度，将重要度取值最大的部分节点作为关键道路的候选节点，最后对选取的节点进行连通性的检查从而生成一条关键道路。根据上述方法，在成都市路网中存在的1 484个路段提取10条关键道路。具体的提取结果如图1所示。

图1 成都市路网十条关键道路

在上述实验条件下，为了得到稳定的仿真结果，m的取值与路网的平均路径长度有着一定关系。当m取值小于路网平均路径长度时评估结果是不稳定的，而m取值大于路网平均路径长度时评估结果趋于稳定。图2是对成都市路网1 484个路段用本文的评估方法得到的路段重要性的值及度与介数的关系，其中m＝4，m取值为大于路网的平均路径长度，因为这种情况下评估结果趋于稳定。从这个关系图中可以看出，整体的趋势是度大的节点的重要性较大，但是这种线性关系也不是处处成立的，图2中有大量度相同的节点，这些度相同的节点是无法用基于度的评估方法得出精确的评估结果的，另外特别是在度较大的区域还会出现随着度的增加重要度降低的情况。

表1是抽取度为1的所有的路段，从表中可知这18个路段采用基于度的评估方法无法得出精确结果，而采用本文的方法，表格的最后一列能得出精确的评估结果。

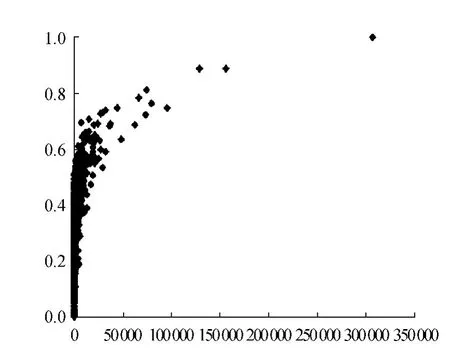
图2 道路重要度与度的关系

表1 道路重要度与度的关系

图3是对1 484个路段用本文的评估方法得到的路段重要性的值与介数的关系。从这个关系图中可以看出，整体的趋势是介数较大的节点的重要性较大，但是这种线性关系也不是处处成立的，图3中也有大量的介数相同的节点，这些节点是无法用基于介数的评估方法得出精确的评估结果的，另外特别是在介数较大的区域还会出现随着介数的增加重要度降低的情况，如图3图形接近顶端的部分。

表2是抽取了介数为1的所有的路段，从表中可知这36个路段采用基于介数的评估方法无法得出精确结果，而采用本文的方法，表格的最后一列能得出精确的评估结果。

图3 道路重要度与介数的关系

表2 道路重要度与度的关系

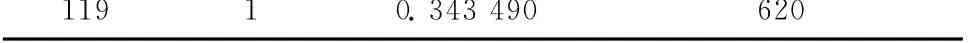
119 1 0．343 490 620

为了验证本文的评估算法的精确性，抽取图1中的一条关键道路来验证本文的算法。这条关键道路的路段节点的序号为：1 417、1 429、1 430、1 435、1 455、1 448、1 458、1 466、1 460、1 462、1 436、1 439、1 465、1 437、1 432、1 416、1 424、1 441、62、1 421。表3是这一关键路径在基于度的方法基于介数的方法与本文的评估方法的结果的对比。表中第五列数据是基于度的评估方法的排序结果，度越大的节点与周围节点的连接分枝越多，那么这种节点就越重要，但是存在着像1 432与1 416这样的度相等的路段无法得出评估结果。表中第六列数据是基于介数的评估结果，介数反应了路网中的所有最短路径经过该路段的数量，介数越大的路段节点所承载的交通流量也就越大，因此这一评估方法反应了路段的承载能力，关键路径中虽然1 439号路段与1 430号路段相比有着较大的度，但从介数的计算结果看1 430的介数为128 536而1 439的介数为73 865，这表明在实际的路网中1 430所承载的流量要比1 439大得多，因此从路网的实际流量角度看1 430号路段更为重要。表中最后一列数据为本文的评估方法的结果，这一评估结果是同时考虑了度和介数两大因素并且把路段的重要度看成与其m阶邻接节点有关，在该方法的评估结果中1 432与1 416这样的度相等的路段节点在本文方法中能够进一步取得更精确的评估结果。在基于介数的评估结果中1 448与1 435号路段相比前者的介数大于后者，但是1 435号路段在本文的评估方法中与周围m阶节点的影响更大，因此在本文的评估结果中1 435号路段的重要性更高。

表3 关键路径上路段重要性评估结果

3 结 论

路段重要性评估方法是路网规划、设计与路网可靠性研究中的关键技术。目前的路段重要性评估中缺乏考虑全局性的评估方法。本文提出在复杂路网的对偶拓扑结构的基础上，研究基于m阶邻居节点的路段节点重要性的多因素评估模型。在试验中选用成都市GIS路网在其对偶拓扑结构上验证基于度与介数的两大因素评估模型。实验结果表明：本文所提出的研究方法与介数法和基于度的方法相比具有较高的评估准确性。该研究进一步揭示路网中路段节点的相互影响和依赖的作用机制，为研究复杂路网的路段重要性提供一种新的研究方法。

［1］ 赫南，李德毅，淦文燕，等．复杂网络中重要性节点发掘综述［J］．计算机科学，2007（12）：1－5．

［2］ 熊金华，曹亚妮，程越．基于统计分析方法的地理要素显示重要性确定研究［J］．测绘工 程，2012，21（3）：26－30．

［3］ TAYLOR M A P．Applying interactive color graphics in traffic planning［J］．Co mputers ＆ Graphics，2007，11（3）：241－248．

［4］ 王晓丽，温冬海，张利分．交通网络重要路段确定方法研究［J］．山西科技，2007（1）：91－95．

［5］ 侯立文，蒋馥．城市道路网中路段相对重要性研究［J］．系统工程理论方法与应用，2004，13（5）：425－428．

［6］ 刘思峰，万寿庆，陆志鹏，等．复杂交通网络中救援点与事故点间的路段重要性评价模型研究［J］．中国管理科学，2009，17（1）：119－124．

［7］ 王少华，钟耳顺，张小虎，等．北京交通网络拓扑结构及可达性格局历史文化研究［J］．测绘与空间地理信息，2014，37（1）：9－12．

［8］ 周兰兰，康建荣．拓扑多边形自相交判断及纠正方法［J］．测绘与空间地理信息，2014，37（10）：33－35．

［9］ 李玉兰，李耀堂．城市道路网容量的对偶图算法［J］．云南大学学报：自然科学版，2006（4）：293－297．

［10］徐英睿，陆锋，张洪岩．基于对偶图的城市交叉口延误分析［J］．公路，2012（9）：149－153．

［11］闫文彩，张玉林，赵茂先，等．基于复杂网络的城市路网可靠性分析［J］．山东科学，2011（2）：65－70．

［12］刘刚，李永树，杨骏，等．对偶图节点重要度的道路网自动选取方法［J］．测绘学报，2014，43（1）：97－104．