Ne Quick2电离层改正模型的性能评估

李施佳，蔡昌盛，2，戴吾蛟，2，易志鹏

（1．中南大学 地球科学与信息物理学院，湖南 长沙410083；2．湖南省精密工程测量与形变灾害监测重点实验室，湖南 长沙410083；3．国网湖南省电力公司培训中心电力营销培训分部，湖南 长沙410131）

伽利略卫星导航系统是欧盟正在建设的世界上第一个向民用开放的商业全球导航定位系统。目前，利用星座中已有的4颗伽利略在轨验证卫星进行伽利略单系统定位已经变成现实。在不久的将来，更多的伽利略卫星将在轨运行，提供导航和定位服务。不同于GPS利用Kl obuchar模型［1］改正电离层误差，伽利略系统采用Ne Quick模型［2］对电离层误差进行改正以服务于单频接收机用户。电离层改正模型性能的好坏直接关系到用户的定位精度，因此Ne Quick电离层模型性能如何已成为业界普遍关心的问题。

对于Ne Quick模型，国内外已有学者进行了相关 研 究。Astaf yeva 等［3］利 用 GNSS 数 据 对Ne Quick、Klobuchar和IRI模型进行了比较研究；Jodogne等［4－5］利用 GPS台站资料对 Ne Quick模型进行了评估。李子伟分析了Ne Quick模型的精度［6］；杨哲、王军等研究了Ne Quick模型在中国区域 的 应 用［7－8］。 自 从 Ne Quick 改 进 模 型 （即Ne Quick2）于2008年被学者提出［9］后，Ne Quick2模型得到了极大关注。Ne Quick2模型改进了Ne Quick1模型底部和顶部的电离层解析式及相关参量，优化了计算，相比Ne Quick1具有明显的变动。已有文献大多基于Ne Quick1进行研究，但Ne Quick1已逐渐被Ne Quick2所取代。基于此，本文对Ne Quick2电离层改正模型进行了性能评估。

1 NeQuick模型

Ne Quick模型［2］由意大利萨拉姆国际理论物理中心的高空物理和电波传播实验室与奥地利格拉茨大学的地球物理、气象和天体物理研究所联合研究而成，该模型已经在欧空局进行了应用［4］，是伽利略系统广播星历采用的电离层改正模型。

Ne Quick模型是一种三维电离层电子密度模型，利用该模型可以计算给定任何时间和空间位置的电子密度，通过对信号路径上的电子密度进行积分，可以得到任意路径上的总电子含量。随着伽利略系统建设的推进，Ne Quick模型也在不断更新，目前最新版本为Ne Quick2。Ne Quick2模型取消了原Ne Quick1模型对F10．7指数最高上限为193的限定，使得模型与实际情况符合的更好。为了更好地反映实际电离层的变化，Ne Quick2模型对原模型的底部和顶部的电离层解析式及相关参量进行了改进，采用与月份无关的经验参数，计算效率得到了提高。

Ne Quick2模型需要输入的信息为12个CCIR系数文件和地磁纬度文件。在利用该模型计算斜路径电子含量时，基本输入参数为：信号传播路径上两端点的地理坐标（经纬度）和高度、月份、世界时以及太阳活动参数（R12或F10．7）。伽利略系统为了给用户提供实时电离层延迟改正值，用与地磁纬度有关的有效电离因子代替输入参数F10．7。有效电离因子可通过导航电文参数计算得到。Ne Quick2模型具体公式可参见文献［9］。

2 数据处理结果与分析

GPS观测数据来自香港卫星定位参考站网，选取了HKOH及HKFN两测站于2012年3月20日至24日的观测数据进行计算。Ne Quick2模型需要的CCIR系数和地磁纬度文件来自国际电信联盟无线电通信部的数据库。F10．7值从美国国家海洋和大气管理局气象预报中心获得。基于观测数据中的双频伪距观测值，获得每颗卫星的斜向总电子含量（STEC）。在输入相应的F10．7值、测站位置、卫星位置和时间信息后，便可利用Ne Quick2模型获得斜向总电子含量。最后将其与实测的斜向总电子含量求差来评估模型的精度。

为了更好地阐述Ne Quick2模型的性能，将其与国际参考电离层（IRI）［10］和 Klobuchar模型［1］结果进行了对比。IRI模型是IRI工作组基于大量的探测资料和研究成果开发的全球电离层模型。该模型可获得任一时间、地点上空50～2 000 k m范围内的电子密度及路径上的电子含量的月平均值，是目前国际上最有效且被广泛认可的电离层经验模型，本文利用IRI2007模型进行计算。Klobuchar模型为单层模型（高度为350 k m），该模型反映了电离层延迟的周日变化特性。单频GPS接收机普遍采用此电离层延迟改正模型进行电离层误差改正。

利用2012年3月20日03：30至06：00香港HKFN测站的观测数据计算了截止高度角为30°时每颗GPS卫星的实测斜向总电子含量值，将其作为参考来评价Ne Quick2模型，并与IRI和Klobuchar模型的结果进行对比。各电离层模型斜向总电子含量计算值与GPS实测值差值结果如图1所示。

图1 3种电离层模型与实测斜向总电子含量的差值

图1 给出了对应每颗卫星的实测斜向总电子含量值与模型计算得到的斜向总电子含量的差值。由于利用GPS观测值获得的斜向总电子含量值中还包含GPS码间偏差的影响，故在图1中对应每颗卫星的差值曲线均含有一常数项系统偏差［11］。由图1可以看出，IRI模型对应的PRN18和PRN22卫星偏差值的变化幅度相对其它卫星较大。3个不同的电离层模型计算的斜向总电子含量值变化趋势较为一致。从图1（c）中可以看出，部分卫星的曲线相比图1（a）和图1（b）更接近0轴附近，但实测的斜向总电子含量中包含GPS码间偏差的影响，因此与实测值差异小并不能说明该模型具有更高的精度。

由于GPS码间偏差在短时间内可以当作一个常数来处理，通过求取标准差来分析各个电离层模型求取的斜向总电子含量与实测值的差异。表1给出了对应每颗卫星各模型得到的斜向总电子含量值与实测值差异的标准差。

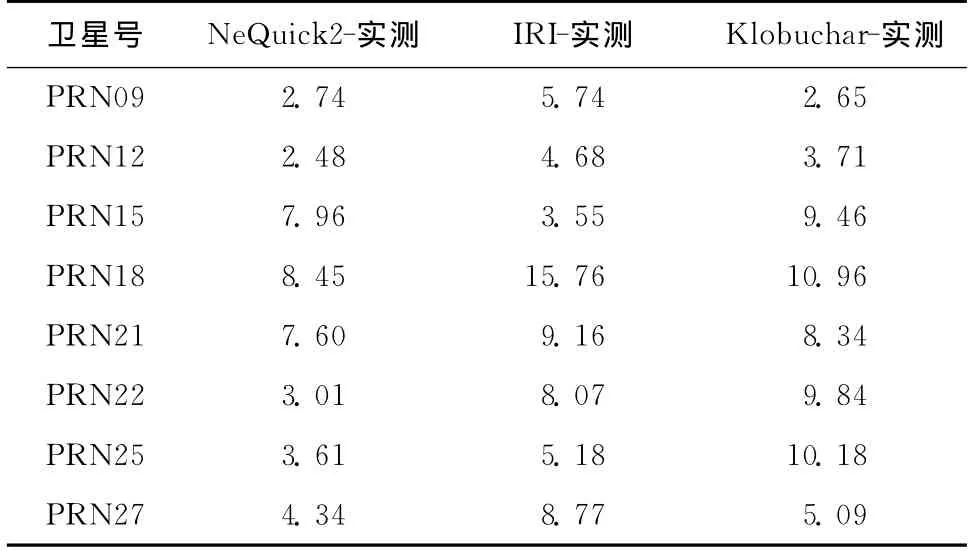
表1 实测值与模型得到的斜向总电子含量值的差值标准差 TECU

由表1可以看出，除卫星PRN15外，Ne Quick2对应每颗卫星的标准差值最小，反映Ne Quick2模型获得的电离层斜向总电子含量值与实测值具有更好的一致性。

为了分析卫星截止高度角的影响，分别计算了卫星截止高度角为30°及60°时，2012年3月20日香港HKOH测站对应每颗卫星的模型与实测斜向总电子含量差值，其结果分别如图2（a）和图2（b）所示。其差值的标准差统计如表2所示。

图2（a）和图2（b）分别对应截止高度角为30°和60°的情况。图中横轴代表相应截止高度角下各卫星的有效历元个数，纵轴代表模型与实测斜向总电子含量差值，单位为TECU。图中每一条曲线代表一颗卫星。由图2可以看出，在卫星截止高度角设置为30°时，对应IRI模型的斜向总电子含量差值在一个更大的范围内变化。当截止高度角为60°时，3种模型计算的斜向总电子含量趋势较为一致。相比而言，Ne Quick2和Klobuchar模型在低高度角时具有更好的稳定性。由表2可以看出，当截止高度角设置为60°时，3种模型与实测斜向总电子含量差值的标准差均大幅减小，其中IRI模型精度提升最高。两种情况下，Ne Quick2模型与实测差值的标准差最小，而Klobuchar模型与实测差值的标准差最大，表明Ne Quick2模型具有更好的稳定性。

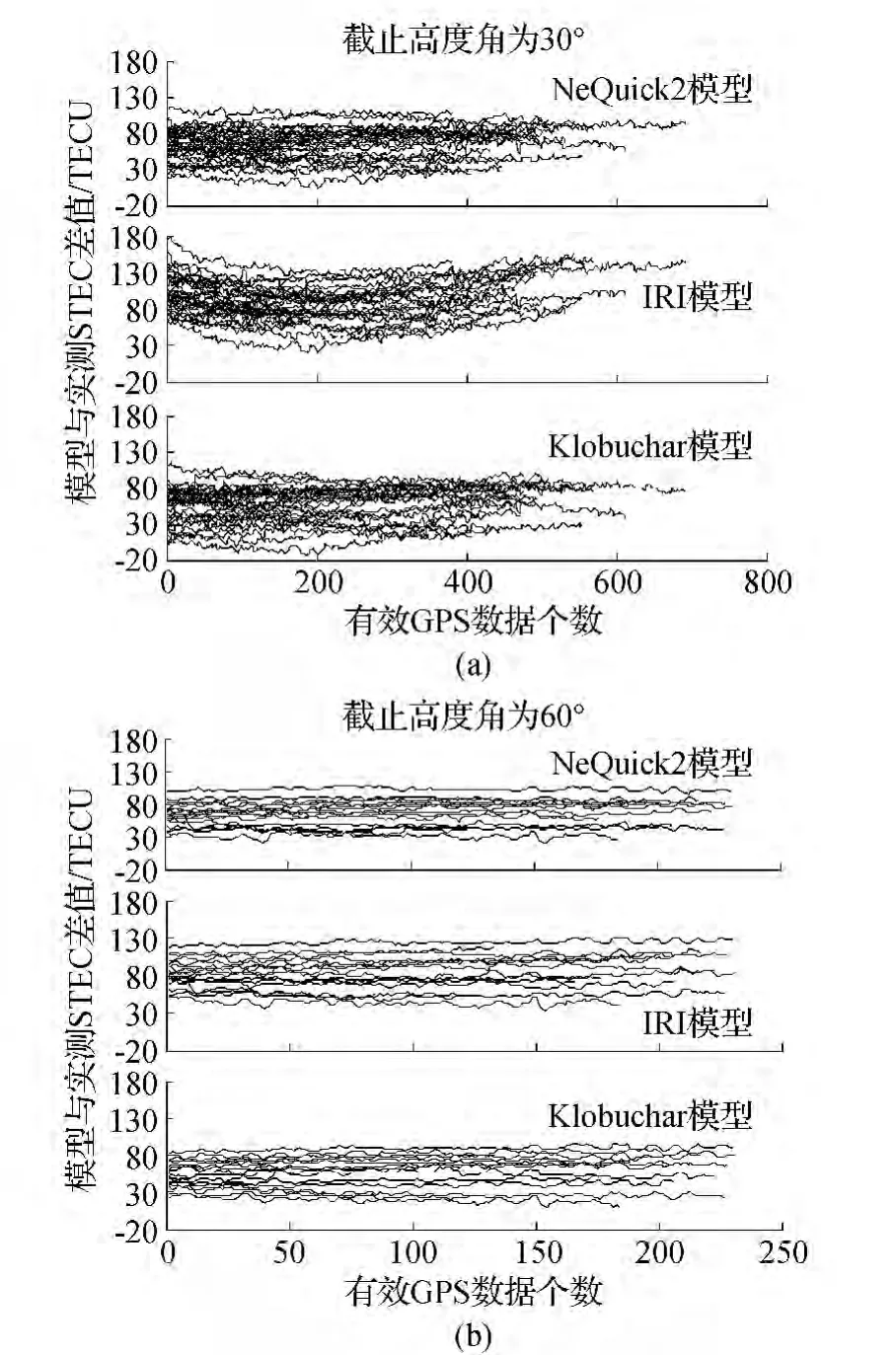
图2 各模型计算值与实测斜向总电子含量值的差值

表2 不同截止高度角各模型计算值与实测斜向总电子含量差值的标准差

为减小卫星高度角对模型精度的影响，本文计算了截止高度角为60°时，2012年3月20至23日共4 d香港HKOH测站模型计算与实测斜向总电子含量差值的标准差，其结果如图3所示。

图3 实测值与模型得到的斜向总电子含量差值的标准差

由图3可以看出，Ne Quick2模型与实测斜向总电子含量差值的标准差保持在15 TECU以内，Ne Quick2相比IRI和Kl obuchar模型，计算的斜向总电子含量与实测值在绝大多数情况下具有更好的一致性。

3 结束语

通过对比不同高度角情况下Ne Quick2模型、IRI模型、Klobuchar模型与实测斜向总电子含量的差值，结果表明，IRI模型对高度角较为敏感，在卫星高度角较低时获得的斜向总电子含量与实测值差值较大。相对而言，Klobuchar模型和Ne Quick2模型受卫星截止高度角影响小。根据各电离层模型计算的斜向总电子含量与实测差值的标准差统计结果，Ne Quick2模型与实测斜向总电子含量差值的标准差保持在15 TECU以内，Ne Quick2模型计算值与实测值具有更好的一致性。

［1］ KLOBUCHAR J A．Ionospheric ti me－delay algorith m f or single－frequency GPS users［J］．Transactionson Aerospace and Electronic Systems，1987，23（2）：325－331．

［2］ GIOVANNI D I，RADICELLA S M．An analytical model of the electron density profile in the ionosphere．Advances in Space Research，1990，10：27．

［3］ ASTAFYEVA E I，AFRAI MOVICH E L，OINATS A V，et al．Dynamics of global electron content in 1998–2005 derived fro m global GPS data and IRI modeling［J］．Advances in Space Research，2008，42：763－769．

［4］ JODOGNE J C，NEBDI H，WARNANT R．GPS TEC and ITEC fro m digisonde data co mpared with NEQUICK model［J］．Advances in Space Research，2004，2：269－273．

［5］ ZHANG MANLIAN，S M RADICELLA，SHI JIANKUI，et al．Co mparison among IRI，GPS－IGS and ionogram－derived total electron contents［J］．Advances in Space Research，2006，37（5）：972－977．

［6］ 李子伟，陈若夫，张勇，等．区域单频GNSS用户经验电离层模式修正效果评估［J］．工程地球物理学报，2009，6（5）：668－673．

［7］ 杨哲，宋淑丽，薛军琛，等．Klobuchar模型和Ne Quick模型在中国地区的精度评估［J］．武汉大学学报：信息科学版，2012，37（6）：704－708．

［8］ 王军，党亚民，薛树强．Ne Quick电离层模型在中国地区的应用［J］．测绘科学，2007，32（4）：38－40．

［9］ NAVA B，COISSON P，RADICELLA S M．A New Version of the Ne Quick ionosphere electron density model［J］，Journal of At mospheric and Solar－Terrestrial Physics，70，2008，P1856－1862．

［10］BILITZA D．International Reference Ionosphere 2000［J］．Radio Sci．，2001，36（2）：261－275．

［11］孟范伟，郭英，刘振．电离层异常原因分析与建模［J］．测绘与空间地理信息，2014，37（1）：215－218．