基于小波变换和曲波变换的图像边缘检测新算法*

罗晓霞，王莉青，薛弘晔

(西安科技大学计算机学院，陕西 西安 710054)

基于小波变换和曲波变换的图像边缘检测新算法*

罗晓霞，王莉青，薛弘晔

(西安科技大学计算机学院，陕西 西安 710054)

针对图像处理中的边缘检测问题，提出了一种基于小波变换和曲波变换的图像边缘检测新算法。首先对原始图像进行小波变换得到小波边缘图像；然后对原始图像进行曲波变换并使用Canny算子得到曲波边缘图像；最后基于小波变换的窗口内边缘强度自适应融合算法将小波边缘图像和曲波边缘图像进行融合得到最终边缘图像。该方法结合了小波变换描述图像细节特征的优势和曲波变换处理曲线或直线边缘特征的优势，能全面刻画边缘图像的纹理与细节信息，提高了图像清晰度。仿真实例表明了该算法的有效性。

曲波变换；小波变换；边缘检测；自适应融合算法

1 引言

图像边缘信息表达了图像的基本内容和结构，是图像的基本特征之一，是分析和识别图像的基础，因而，研究有效的边缘检测算法具有重要意义。它广泛应用于目标识别、拓片图像分析、医学图像分析等领域。关于图像的边缘检测问题，该领域的学者已经做出了大量而卓有成效的工作，其中小波变换和曲波变换是数字图像处理的发展过程中逐渐被认识和使用的两种边缘检测方法。小波变换广泛应用于图像处理、图像识别、数据去噪等方面[1,2]。由于小波变换具有时频局部化性质及多分辨的能力，1989年Mallat S等人[3,4]提出了用小波检测多尺度边缘的理论，并将小波变换与梯度方法结合起来，得到不同分辨率边缘图像，形成了多尺度边缘检测器。小波变换具有描述图像细节特征的优势，小波变换能够有效地提取图像奇异点信息进行图像边缘检测，但是它的各项同性导致边缘信息不能完全显示，在图像处理方面也会导致信息缺失。Candès E J和Donoho D L[5,6]提出的曲波变换具有各项异性以及局部时频分析的能力，同时又有很强的方向性选择，能全面地表达图像线型边缘信息。曲波变换在处理曲线或者直线边缘特征方面具有独特优势，具有良好的局域化特性以及多尺度分析能力，但是对于点奇异性检测效果较差，过强的线性表达能力会使得细节发生变化，点细节也会有所缺失。针对图像处理中的边缘检测问题，本文提出了一种基于小波变换和曲波变换的图像边缘检测新算法。首先对原始图像进行小波变换得到小波边缘图像；然后对原始图像进行曲波变换并使用Canny算子得到曲波边缘图像；最后基于小波变换的窗口内边缘强度自适应融合算法将小波边缘图像和曲波边缘图像进行融合得到最终边缘图像。该方法结合了小波变换描述图像细节特征的优势与曲波变换处理曲线或直线边缘特征的优势，它能全面刻画边缘图像的纹理与细节信息，提高了图像清晰度。

2 基础理论

2.1 离散小波变换

小波变换的最大优势在于其动态自适应性，即它的窗口面积固定不变，而窗口长度及宽度可以自动变化，能够根据需要对信号的高频部分及低频部分具体分析，提取信号中的有效信息。

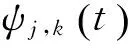
ψj,k(t)=2j/2ψ(2jt-k)

(1)

得到离散小波。

相应的离散小波变换表示为:

Wf(j,k)=(f(t),ψj,k(t))

(2)

小波变换通过参数j、k的调节，从而实现在频域与时域方面的局部化作用。

2.2 离散曲波变换

曲波变换适合于分析具有曲线或者超平面奇异性高维信号，不仅具有时频分析的能力，而且具有较强的方向选择和辨识能力，对图像边缘的表达能力较强[7]。

定义在笛卡尔坐标系下，离散曲波变换的表达式为:

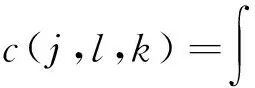
(3)

(4)

其中，W表示半径窗，V表示角度窗。

(5)

Vj(ω)=V(2[j/2]ω2/ω1)

(6)

2.3 Canny算子

Canny算子是用高斯函数平滑图像，用一阶偏导的有限差分来计算图像梯度的幅值和方向，之后对梯度幅值进行非极大值抑制，最后用双阈值算法检测和连接边缘。Canny算子进行边缘检测时，高斯平滑函数定义为：

(7)

计算在x和y方向上的一阶偏导，将二维的滤波器模板分解为两个一维的滤波器卷积模板：

(8)

(9)

其中，σ是高斯滤波器的空间尺度系数，用于控制图像平滑的程度。

将式(8)与式(9)分别与图像f(i,j)做卷积，得到平滑滤波后的输出：

P(i,j)=Gx*f(i,j)，Q(i,j)=Gy*f(i,j)

(10)

每个像素点梯度幅值T(i,j)和梯度方向θ(i,j)分别为：

(11)

θ(i,j)=arctan(Q(i,j)/P(i,j))

(12)

2.4 边缘图像融合

由于边缘图像只保留了图像的边缘信息，而且为了使融合后图像的边缘效果达到最佳，选取基于小波变换的窗口内边缘强度自适应融合算法。基本思想：选定窗口，计算窗内各像点的边缘强度，并以归一化的边缘强度作为权值对两幅图像的高频系数进行加权求和。

点(x,y)处的边缘强度定义为：

m=1,2

(13)

(14)

将小波边缘图像与曲波边缘图像融合后，得到的最终边缘图像用F(x,y)来表示，则F(x,y)中像素点(x,y)的像素值D(x,y)表示为：

(15)

3 新的边缘检测算法

3.1 基本思想

新的边缘检测将小波变换与曲波变换相结合，利用二者的优势进行图像边缘检测。算法流程如图1所示。

首先，对原始图像进行预处理，使其在几何特性、灰度级别方面满足变换需要。

然后，对预处理后的图像进行小波变换，并根据高频小波系数阈值得到小波边缘图像。

再次，对预处理后的图像进行曲波变换，得到的近似系数作为FINE层系数，使FINE层系数光滑性更好并舍去细节信息，存放在各层的近似系数中，从而得到DETAIL层系数。对DETAIL层继续进行分解，从中确定理想系数，通过Canny算子作用于DETAIL层系数，从而提取出曲波边缘图像。

最后，利用小波变换的窗口内边缘强度自适应融合法将小波变换所得到的边缘图像与曲波变换所得到的边缘图像融合，得到最终的边缘图像。

Figure 1 Algorithm flowchart

3.2 算法描述

算法 基于小波变换和曲波变换的图像边缘检测算法

输入：原始图像及小波变换、曲波变换、Canny算子和融合算法参数。

输出：边缘融合图像。

步骤1 图像预处理：输入原始图像，调整图像尺寸，并利用smooth函数对图像进行平滑处理，得到预处理后图像A；

步骤2 提取小波边缘图像：通过公式(1)以及Mallat快速算法作用于图像A，提取小波系数，根据阈值得到小波边缘图像B；

步骤3 提取曲波边缘图像：对图像A进行曲波变换，对变换后得到的系数进行置零处理，提取保留FINE层系数和DETAIL层系数的图像，将Canny算子作用于DETAIL层系数得到曲波边缘图像C；

步骤4 图像重构与融合：将小波变换所得到的边缘图像B与曲波变换所得到的边缘图像C融合，得到最终融合图像D；

步骤5 评价：对融合图像D进行质量评价,若融合质量不满足要求，重新选择算法参数并返回步骤1，否则转下一步;

步骤6 输出结果图像D。

4 仿真实验

4.1 实验评价

对于边缘检测算法性能的评价，本文选取信噪比(SNR)函数、峰值信噪比(PSNR)函数来描述，其中MSE为融合图像D与标准参考图像R的均方误差:

(16)

(17)

其中，M、N分别为图像的行与列；Dmax为融合图像D的最大值。

(18)

其中，f(x)是边界为[-w,w]滤波器的脉冲响应，G(x)表示边缘，n0是高斯噪声的均方根。

4.2 实验结果

为了测试本文提出的基于小波变换和曲波变换的图像边缘检测新算法的有效性，使用Matlab 7.0语言编写了相应的计算机程序。选取Lena 原图和作者自选图像分别使用小波变换、曲波变换和本文提出的算法得到各自的边缘图像。实验参数选取如下：小波变换尺度参数j=6，平移参数k=7，高低阈值分别取Thmax=40，Thmin=20；曲波变换尺度系数j=20，角度系数l=1。实验结果如图2和图3所示。

Figure 2 Lena image results

Figure 3 Optional image results

从图2和图3得到的实验结果可以看出，经曲波变换处理的图2b很好地描述了原图像的线条纹理部分，将图像的大体轮廓描绘了出来，但细节信息描述欠缺。经小波变换处理之后的图2c在细节部分描述得细致入微，线型内容却欠缺了很多，整体信息不够全面。从图3c的边缘效果来看，图中校门信息缺失量更为明显，但是树叶信息丰富了很多。图2d和图3d是由新的边缘检测算法所得到的边缘图像，它结合了小波边缘检测与曲波边缘检测的优越性，将线条纹理与细节信息都展现了出来，从边缘效果可以看出新的边缘检测算法描述出来了图像大体轮廓，同时提炼了图像边缘细节，边缘信息较全面。

表1与表2是图像原图、经小波变换、曲波变换、新的边缘检测算法得到的信噪比以及峰值信噪比结果。从表1和表2可以看出，新的边缘检测算法得到的边缘图像质量好于小波变换、曲波变换得到的边缘图像。

Table1 Evaluation of Lena edge image

Table2 Evaluation of optional edge image

5 结束语

本文提出的新的边缘检测算法，将曲波变换处理图像线条纹理方面的优势与小波变换对图像细节描述的特点有机地结合起来，共同进行图像边缘检测。实验表明，该算法提升了边缘图像总体轮廓的清晰度，丰富了边缘细节信息方面的描述，边缘线性结构也得到了凸显，边缘检测结果较为满意。实验评价结果表明了新的边缘检测算法得到的边缘图像质量较好。

[1] Gao Shan, Ma Yan-hui. Algorithm research of filtering for SAR images based on edges-preserving [J]. Journal of Liquid Crystals and Displays, 2013,28(2):290-294.(in Chinese)

[2] Niu Sheng-xiao, Wang Sheng, Yang Jing-jing, et al. A fast image segmentation algorithm fully based on edge information [J]. Journal of Computer-Aided Design & Computer Graphics, 2012,24(11):1410-1419.(in Chinese)

[3] Mallat S. Multifrequency channel decompositions of images and wavelet models[J]. IEEE Transactions on Acoustic Speech and Signal Processing, 1989, 37 (12):2091-2110.

[4] Mallat S, Zhong S. Characterization of signals from multiscale edges[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992,14(7):710-732.

[5] Starck J L, Candès E J, Donoho D L. The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing, 2002, 11(6):670-684.

[6] Candès E J, Demanet L, Donoho D L. Fast discrete curvelet transforms[J].SIAM Multiscale Modeling and Simulation, 2006, 5(3):861-899.

[7] Zhang Yun-qiang,Zhang Pei-lin,Ren Guo-quan,et al. Invariant moment extraction by curvelet transform for wear particle images[J] . Journal of Image and Graphics, 2012,17(2):263-268.(in Chinese)

附英文参考文献:

[1] 高珊，马艳会.基于边缘保持的SAR图像滤波算法研究[J] .

液晶与显示, 2013,28(2):290-294.

[2] 钮圣虓，王盛，杨晶晶，等.完全基于边缘信息的快速图像分割算法[J] . 计算机辅助设计与图形学学报, 2012,24(11):1410-1419.

[7] 张云强，张培林，任国全，等.曲波变换用于磨粒图像不变矩的提取[J] .中国图象图形学报, 2012,17(2):263-268.

LUO Xiao-xia,born in 1964,associate professor,her research interests include database,software engineering, and software development.

王莉青(1986-),女,山西隰县人，硕士，研究方向为计算机图形图像处理。E-mail:490891237@qq.com

WANG Li-qing,born in 1986,MS,her research interest includes computer graphics, and image processing.

薛弘晔(1960-),男,陕西扶风人，博士，教授，研究方向为网络与高性能计算、图像实时处理技术。E-mail:xuehy60@163.com

XUE Hong-ye,born in 1960,PhD,professor,his research interests include network and high performance computing, real-time image processing technology.

A novel algorithm of image edge detection based on wavelet transform and curvelet transform

LUO Xiao-xia，WANG Li-qing，XUE Hong-ye

(School of Computer Science,Xi’an University of Science and Technology,Xi’an 710054,China)

Facing the edge detection problems lying in image processing, a novel algorithm of image edge detection is put forth based on wavelet transform and curvelet transform. Firstly, we process the original image with the method of wavelet transformation and obtain a wavelet edge image. Then we achieve a curvelet edge image by processing the original image with the method of curvelet transformation and the Canny operator. Finally, the final edge image is acquired by merging the wavelet edge image and the curvelet edge image based for the adaptive fusion algorithm on the edge intensity in wavelet transform window. The algorithm combines the advantage of wavelet transform in describing image detail characteristics and the advantage of curvelet transform in processing curve or straight line edge features. It fully characterizes the details and texture information of the edge image, and improves image clarity. Simulation results verify the effectiveness of the algorithm.

curvelet transform;wavelet transform;edge detection;adaptive fusion algorithm

1007-130X(2015)01-0157-05

2013-02-25;

2013-07-03

TP391.4

A

10.3969/j.issn.1007-130X.2015.01.024

罗晓霞(1964-),女,陕西扶风人，副教授，研究方向为数据库、软件工程及软件开发。E-mail:luoxx@xust.edu.cn

通信地址：710054 陕西省西安市雁塔中路58号西安科技大学计算机学院

Address:School of Computer Science,Xi’an University of Science and Technology，58 Yanta Rd Middle,Xi’an 710054,Shaanxi,P.R.China