基于Hopfield网络的飞机设计

中航飞机研发中心结构所 张俊亮 何晓雪 宋云霞

Hopfield网络被广泛应用于多个领域，如在求解组合优化、线性规划以及二次规划中均有涉及。但Hopfield网络也存在着一定的局限，大多数模型在较为复杂的约束问题求解上根本无法应用，对一般非线性约束优化问题来说：第一，在网络拓扑结构、各神经元外部输入确定、各神经元之间的连接权重上进行运用，相对复杂；第二，通过惩罚函数法的应用，将非线性约束优化问题向无约束优化问题进行转化；第三，运用网络进行求解，会产生数值较大的罚参数，这可能导致网络出现饱和截止的现象，最终无法进行仿真求解。受此限制，所得优化结果往往与约束条件有一定的出入。但在优化设计中，约束的满足同样重要。

本文在对约束条件进行处理上选用了Hopfield网络联合增广乘子法的方式，并将高斯噪声信号引入到随机神经网络中对其进行构建，对于随机神经网络中存在的无等温阶段、难以跳出局部极小值的缺点，在对随机网络进行运行时结合了模拟退火算法的等温马尔科夫链和Metropolis准则，使神经网络的寻优能力得到了进一步的提升。

1 喷气教练机的总体参数优化

在本文中，选取的算例包含有两个子模块，分别为质量估算模块和性能计算模块。优化设计设定的变量为燃油质量mf、展弦比x、翼面积s。对喷气教练机进行优化设计的最终目的是在约束条件为航程R=700km，最大平飞速度Vm≥680km/h,巡航速度Vc≥550km/h,着陆速度Vl≤140kmPh,升限H≥14km的前提下将飞机起飞质量m0降至最低。

模型中，目标函数、设计变量与状态变量的量级之间存在着较大的差异，因此，还需要对他们进行进一步的处理，采用的处理方法为归一法，目标处理为m0/3000，转化着陆速度约束条件，使之成为的形式，并模仿此方法对其他约束条件进行一一处理。以下是优化问题的规范形式：

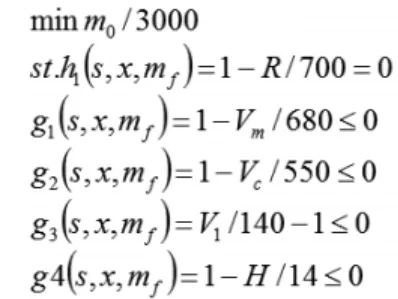
1.1 网络仿真计算与结果

罚参数的递增方式：

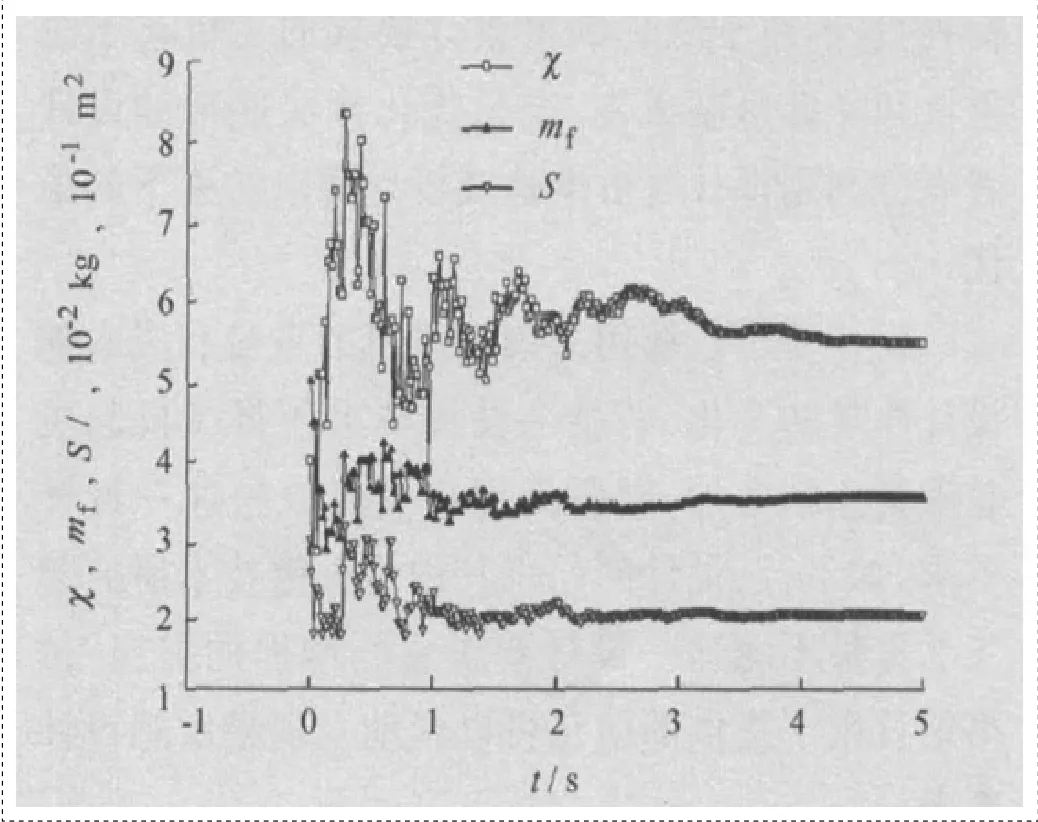
图1 系统随t的变化过程

由图1可知，前期，在高斯噪声的影响下，网络处于波动状态。但随着梯度的的改变，网络会发生相应的收敛直至稳定。不同的初值，最优解及约束满足程度分别在表1和表2中列出。

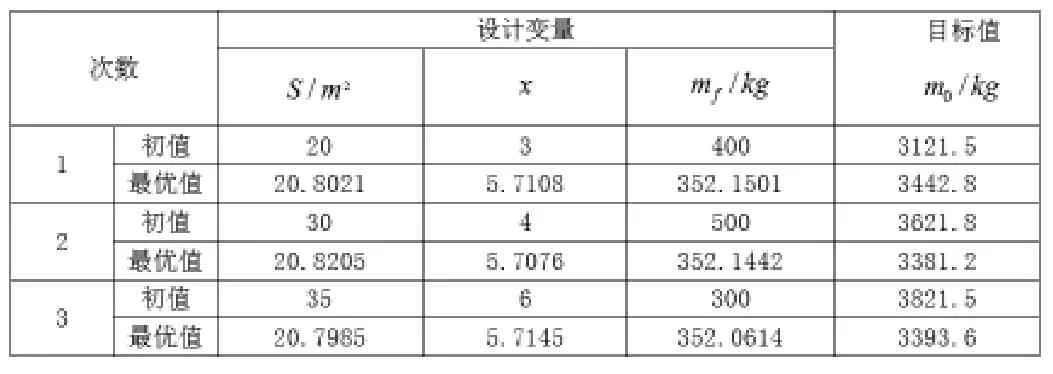
表1 算法结果比较

表2 各最优解的约束满足情况

通过表1和表2我们可以看出，该算法具有精度高，最优解能够充分满足约束条件的特点。无论从何初始值开始，最终网络都能收敛与全局最优解。

1.2 基于拉氏乘子进行权衡研究

在对飞机进行总体概念设计的过程中，权衡研究发挥着无可取代的作用，主要包括设计参数权衡和设计要求权衡两类。

总体参数优化的本质就在于参数权衡的设计，根本目的在于在使设计要求得到充分满足的前提下尽量降低飞机起飞的总重量和飞机的研制成本。而全局优化算法的应用，使设计者在充分满足设计要求约束的前提下对设计自由度进行最大限度的利用，最终实现最优。

随着设计要求的改变，用于对飞机重量和成本进行确定的设计要求权衡也会发生相应的改变。当出现某一设计要求会直接导致飞机起飞总重量出现大幅度的增加时，可向用户进行咨询，看是否可对这一设计要求进行相应的放宽，若不行，设计部门就需要对该设计要求进行重点研究，以最终获得能够有效解决该问题的方法。而拉格朗日乘子可提供最为精确的信息，以协助设计人员发现最敏感的设计要求。

拉氏乘子分量1≠0表示处于该项约束边界，几何意义：在靠近极值点的位置，通过对随着约束条件细微变化而相应发生变化的目标函数变化比率观察，可知起飞总重量m0随升限约束变化比较敏感。如进行相同单位量的放松，相较于其他激活约束，此约束可更多的减少目标。

假设将升限约束条件放松至13km，并对优化模型进行相应的修改，全局寻优后得到最优解为：

﹝19.6934 4.0124 395.0123﹞

此时m0为3214kg，减重5%，各约束对应的拉氏乘子：

﹝-0.2631 0 0 -0.4397 -0.4979﹞

2 干线机的机翼气动/结构综合设计

选取的干线客机载重18870kg，航程4356km，巡航马赫数0.75，对其机翼进行相应的气动/结构设计优化。

整个分析模型包含有3个组成部分，分别为气动、结构和重量。通过基于非等熵全优势方程的（CFDComput ional Fiuid Dynamic)方法与摩擦阻力的工程估算方法的运用，对气动进行相应的分析；运用以工程梁理论为基础的设计方法对结构进行相应的分析；运用处于概念设计阶段的二阶重量估算方法对飞机重量进行估算。

设计变量选取能够从较大程度上影响机翼气动机构的展弦比、根梢比、前缘后掠角、机翼面积、翼根处机翼相对厚度、30%展长处机翼相对厚度、翼梢机翼相对厚度和翼梢扭转角。

为使综合设计的优化模型得到进一步的简化，使大部分气动/结构设计要求得到充分的确保，可在相应分析模型中以其为输入条件进行输入，同时，要求客机的升阻比＞15。最终的优化目标是有效降低机翼重量。

3 结束语

综上所述，神经网络目前所具备的并行分布优势并未能得到充分的开发，它还有巨大的潜力等待着我们去更深入的探索和挖掘，我们相信，随着现代技术的不断革新以及人们对神经网络掌握的进一步深入，再加之硬件仿真手段的创新和发展，神经网络将得到更为广泛的应用，为飞机设计事业创造更大的空间。

[1]周盛强,向锦武.基于Hopfield网络的飞机设计[J].北京航空航天大学学报,2006,32(6):675-679.

[2]叶世伟,郑宏伟,王文杰等.连续时间 Hopfield网络模型数值实现分析[J].软件学报,2004,15(6):881-890.

[3]周盛强.基于Hopfield神经网络和KS函数的优化设计研究[J].飞机设计,2006,(2):8-11.

[4]林盾,李建生.Hopfield网络在系统优化设计中的应用[J].湘潭师范学院学报(自然科学版),2008,30(4):4-7.

[5]金海和.Hopfield网络学习及其在最优化问题中的应用[C].管理科学与系统科学研究新进展.2001:3-8.

[6]董波,张晓东,郦正能,等.干线客机机翼气动/结构综合设计研究[J].北京航空航天大学学报,2002,28(4):435-437.