双尺度方法在粗糙海面中的电磁散射分析和应用

贵州航天计量测试技术研究所 张 凯

自然界中的某些粗糙面同时含有大、小粗糙度或者粗糙度是连续分布的，即有多个尺度的粗糙度。对于这类粗糙面的电磁散射计算，其粗糙度既不在微扰法适用区域又不在基尔霍夫近似方法的适用范围，根据文献[1]单独使用微扰法或基尔霍夫近似方法均不能较客观地反映粗糙面的电磁散射特性。此时可以将表面粗糙度视为大小两种粗糙度的叠加，将微扰法用于小粗糙度，基尔霍夫近似用于大粗糙度，将小粗糙度计算的散射系数在大粗糙度的斜率分布上作集平均，得到总散射系数，即双尺度方法(Two Scal e Met hod,TSM)。

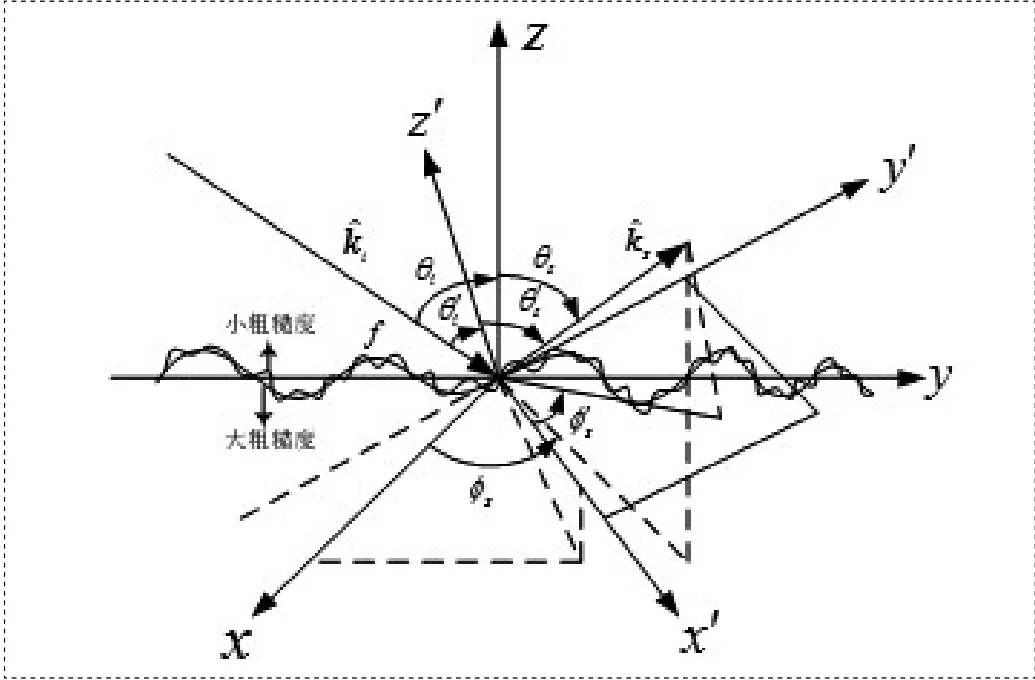
图1 双尺度粗糙面的电磁散射示意图

所以：

当表面斜率为零时，主坐标系与本地坐标系一致。类似地定义水平极化矢量和垂直极化矢量分别为：

一般情况下，主坐标系中的一个水平极化入射波E0在本地坐标系中可以看成一个水平和一个垂直入射波的叠加，即：

在主坐标系与本地坐标系中，分别定义入射波的水平和垂直极化分量。

由于假定小尺度粗糙度和大尺度粗糙度是各自独立地产生的，因此上式的集平均应该分别由两个独立平均运算产生。根据文献[3]中对散射系数的定义，此时的散射系数表示为

式中的集平均仅是针对大尺度粗糙度。其中：

对于大小尺度同时具有高斯型均方根高度和相关长度的粗糙面，在散射系数计算中的谱密度函数以及斜率概率密度函数分别为：

自然界中的实际风驱粗糙海面，其海浪含有起伏较大的重力波和起伏较小的毛细波，前者为大粗糙度，后者为小粗糙度，因此海面可以视为由大尺度重力波和小尺度毛细波叠加而成，这恰能运用本节的双尺度方法对其散射特性进行研究，可以理解其结果的合理性。

以下计算结果均采用文献[4]中的海谱模型，研究了风驱粗糙海面的单、双站散射系数随入射角、散射角、方位角的变化特征。图2给出了分别采用微扰法（仅考虑小粗糙度）、基尔霍夫近似（仅考虑大粗糙度）以及本文的双尺度法（同时考虑大、小两种粗糙度）计算得到随入射角变化的后向散射系数的结果比较。图中各参数均来自文献[4]，l和 分别为粗糙面的相关长度和均方根高度，两者和海谱的形状有关，文献[4]通过对经验海谱进行拟合得到其值，s代表均方根斜率，它是由Munk对实际海面经过实验观测后进行统计分析得到的，风速为14-16节，海水温度20℃，盐度36‰， 为海水的相对介电常数。

通过比较可以看出，在小入射角区域，TSM的计算结果与KA的计算结果一致，在中等入射角区域，TSM的计算结果与SPM的计算结果一致，在曲线的转折处附近TSM与SPM、KA的差异是由于在大尺度的斜率分布上作了集平均，在近掠射角区域曲线的差异是值得修正的。由于KA一般能够较客观地反映大尺度粗糙度的散射特性，SPM一般能够较客观地反映小尺度粗糙度的散射特性，因此，对于这样的粗糙海面，文献[5]在小入射角区域，起伏较大的海浪（一般为重力波）对散射系数的贡献占据主导地位；在中等入射角区域，起伏较小的海浪（一般为毛细波）对散射系数的贡献占据主导地位。图3给出了HH极化下，利用KA和TSM得到的随散射角变化的双站散射系数。从图中可以看出，即使小入射角情形下，KA与TSM的计算结果在大、中散射角下分离，由此可以看出，对于文献[4]中的海谱模型，只有在小入射角、小散射角范围内，KA的计算结果才能与TSM的结果一致。

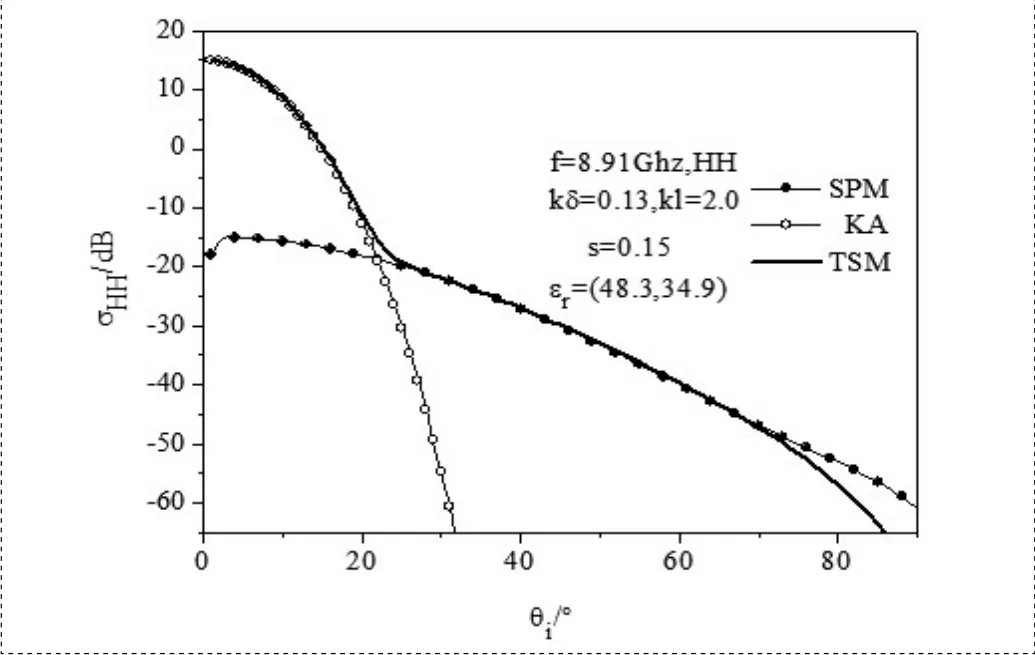
图2 不同方法计算随入射角变化的后向散射系数

图3 不同方法计算随散射角变化的双站散射系数

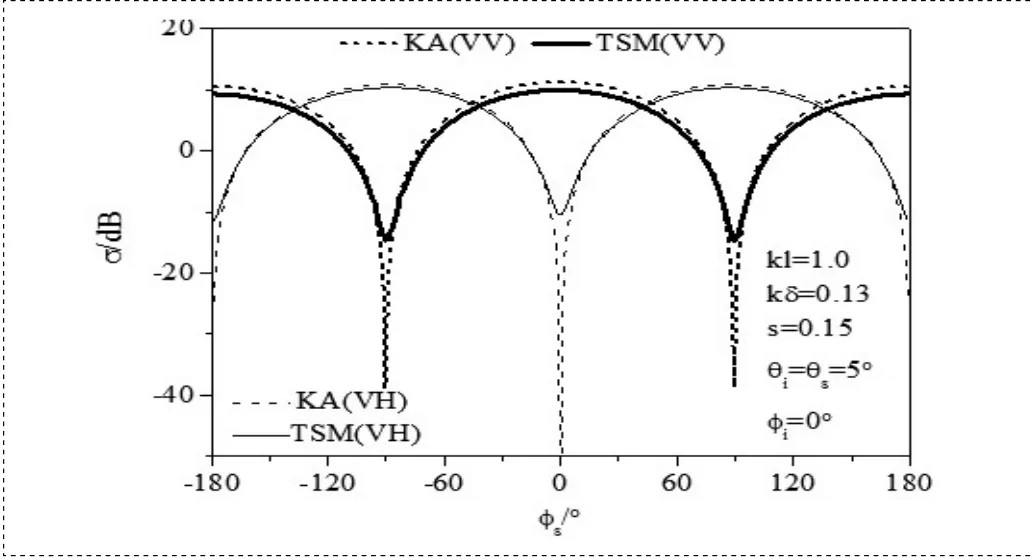
图4 不同方法得到随方位角变化的双站散射系数

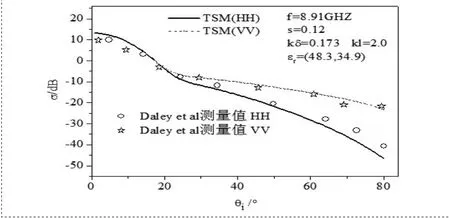
图5 TSM计算结果与实测数据的比较

图4 给出了分别利用KA和TSM得到随方位角变化的双站散射系数曲线的比较。可以看出，同极化（VV）下，在大部分散射方位角区域，KA的结果较TSM的结果偏高，尤其在-180o、0o、180o附近区域；但在-90o和90o附近KA的结果较TSM的结果偏低；交叉极化(VH)下，在-180o～180o内的大部分散射区域，KA的结果较TSM的结果偏高，在-90o、90o方位角左右，偏高最明显，在-180o、0o、180o附近区域，KA的结果较TSM的结果偏低，在0o方位角左右的偏低最明显。图5给出了HH和VV极化下，由TSM得到的随入射角变化的后向散射系数及与相关文献的测量值的比较。风速等各环境参数与图2相同，其它参数如图中所示。可以看出，在大部分入射角区域，TSM结果与文献实测值基本吻合。在大角度下的不一致性，主要是由于未考虑到实际风驱海面上泡沫等离散粒子的体散射对海面的电磁散射的影响，从图中可以看出，HH极化方式下TSM的结果与实测数据差异较VV情形大，据此推理，HH极化方式下泡沫粒子的体散射对海面电磁散射的影响较VV极化情形明显。

[1]金亚秋,刘鹏,叶红霞.随机粗糙面与目标复合散射数值模拟理论与方法[M].北京:科学出版社,2008.

[2]王运华,郭立新,吴振森.改进的二维分形模型在海面电磁散射中的应用[J].物理学报,2006,55(10).

[3]Ulaby F T,Moore R K and Fung A K.Microwave Remote Sensing (Active and Passive) I,II and III.Addison-Wesley,1982.

[4]Wu S T,Fung A K.A noncoherent model for microwave emissions and backscattering from the sea surface.Journal of Geophysical Research,1972,77(30).

[5]王蕊.粗糙面及其与目标复合电磁散射中的相关问题研究[D].西安电子科技大学,2009.