基于Gilbert模型的无线传感器网络报文时间相关丢失率推测算法*

赵 涛

(安徽财经大学 计算机科学与技术系，安徽 蚌埠233000)

0 引 言

在现有传感器网络链路丢失率推测算法中［1～4］，一般都存在链路报文丢失时间无关假设，即认为上一个通过该链路的报文丢失不会对下一报文丢失概率产生影响。但在实际的传感器网络中，报文丢失的主要原因有缓冲区溢出、干扰等，链路发生报文丢失事件，意味着该链路出现拥塞，干扰或节点失效，这就使得下一个通过此链路的报文丢失概率增大。因此，报文丢失在时间上具有较强相关性。

Gilbert 概率模型是一个两状态的马尔科夫模型，描述两个不同时间发生的依赖关系。为解决报文丢失时间相关性问题，本文用Gilbert 概率模型来描述链路报文丢失过程，将Gilbert 模型下的链路报文丢失率推测形式化为Bayesian 概率问题，并用Gibbs 抽样算法来获得链路丢失率的推测值。

1 系统模型

传感器网络受能量和带宽限制，常使用数据汇聚方法收集数据［5，6］，节点在收集所有子节点数据后，将数据发送至下一跳节点(父节点)，直至最后汇聚到Sink 节点。这种汇聚方法通过一个倒立的汇聚树将数据传送到Sink 节点，已经成为延长传感器网络生命能量周期普遍使用的方法。

1.1 网络拓扑模型

用T=(V，L)描述汇聚过程的倒立汇聚树，V 为汇聚过程中所参与传感器节点集合，L 为节点间的链路集合。n为汇聚过程中节点个数，用s 表示汇聚树的根节点，即传感器网络的Sink 节点。用节点对(i，j)∈V×V 表示汇聚树中的链路(数据从节点i 发送至节点j)，节点j 是节点i 的父节点，用f(i)表示，子节点集合用c(i)表示，d(i)表示子孙节点集合。

1.2 报文丢失模型

用随机过程Z=(zi，j)，i∈d(j)，j∈V 表示汇聚树的数据流，用参数对(pi，qi)表示链路l∈L 的时间相关丢失率参数，其中，p 为当前报文通过，下一报文丢失概率;q 为当前报文丢失，下一个报文通过概率。假设传感器网络中所有节点每一轮都发送数据到Sink节点，在每轮数据发送结束后，在Sink 节点可获得各节点发送数据成功或失败信息，用向量表示，其中表示节点k 的数据在第m 轮数据汇聚中是否到达Sink 节点。用向量Xk=表示在N 轮数据汇聚过程中，节点k 每轮数据成功发送情况。0 表示丢失，1 表示成功到达。

2 推测算法

2.1 Gibbs 抽样推测报文丢失率算法

在数据收集结束后，根据统计测量结果Xk推测链路的参数对(pk，qk)的数值。一般来说，在网络逻辑拓扑和报文丢失模型已知的情况下，可利用测量结果推导出导致该结果的联合概率p(Θ|X)，利用Bayesian 推测方法推测出参数值，使后验概率p(Θ|X)取得最大值。

Beta 分布经常作为报文丢失的先验概率分布，假设链路报文丢失的先验概率符合Beta 分布

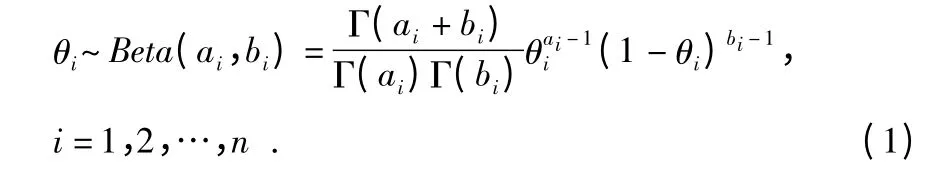
图1 描述了使用Gibbs 抽样方法计算链路报文丢失率，再将此方法扩展至一般网络。

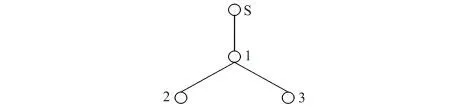
图1 简单的数据汇聚树Fig 1 A simple data aggregation tree

图1 三条链路对应的报文丢失率分别为θ1=(p1，q1)，θ2=(p2，q2)，θ3=(p3，q3)。算法用测量值Xk去推测Θ={(p1，q1)，(p2，q2)，(p3，q3)}。用表示在第m－1 轮节点j 成功接收到节点i 报文的情况下，第m 轮节点j 接收节点i 报文的情况;用表示在第m－1 轮节点j 没有接收到节点i 报文的情况下，第m 轮节点j 接收节点i 报文的情况。令P=［p1，p2，p3］，Q=［q1，q2，q3］，先以计算P=［p1，p2，p3］为例，根据图1 所示拓扑中链路之间的关系可以推导出下面公式(2)

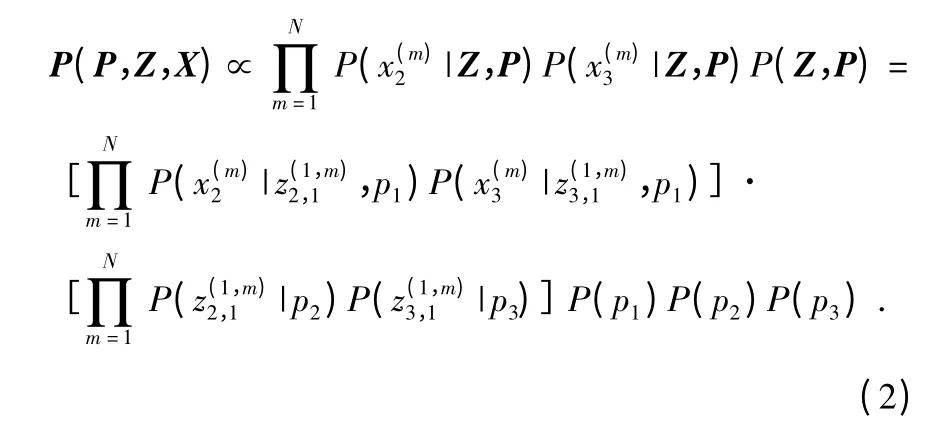
其中

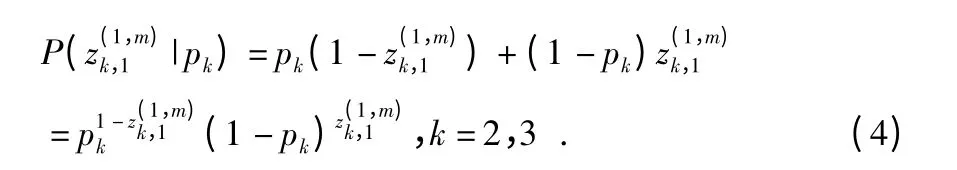
将式(1)、式(3)和式(4)代入式(2)中，可得式(5)

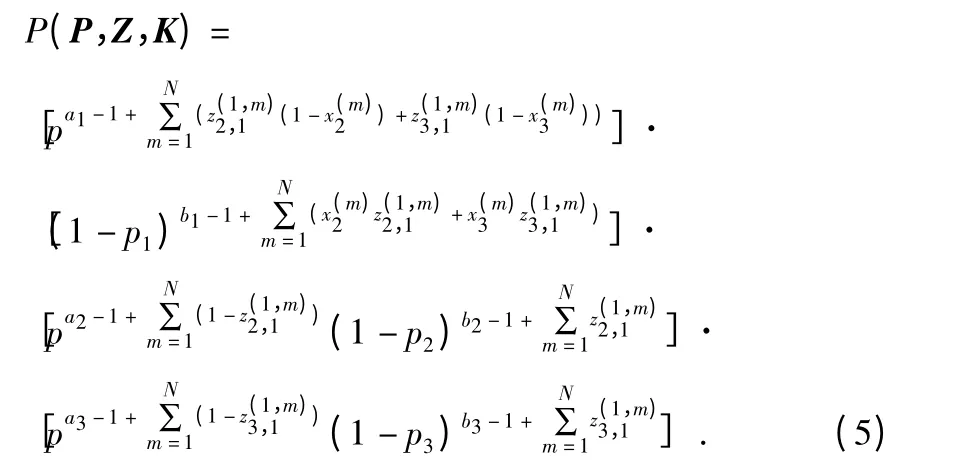
根据公式(5)，可以看出逻辑链路的后验报文丢失P=［p1，p2，p3］的概率分布仍然是Beta 分布，每条逻辑链路报文丢失率对应的Beta 分布分别为

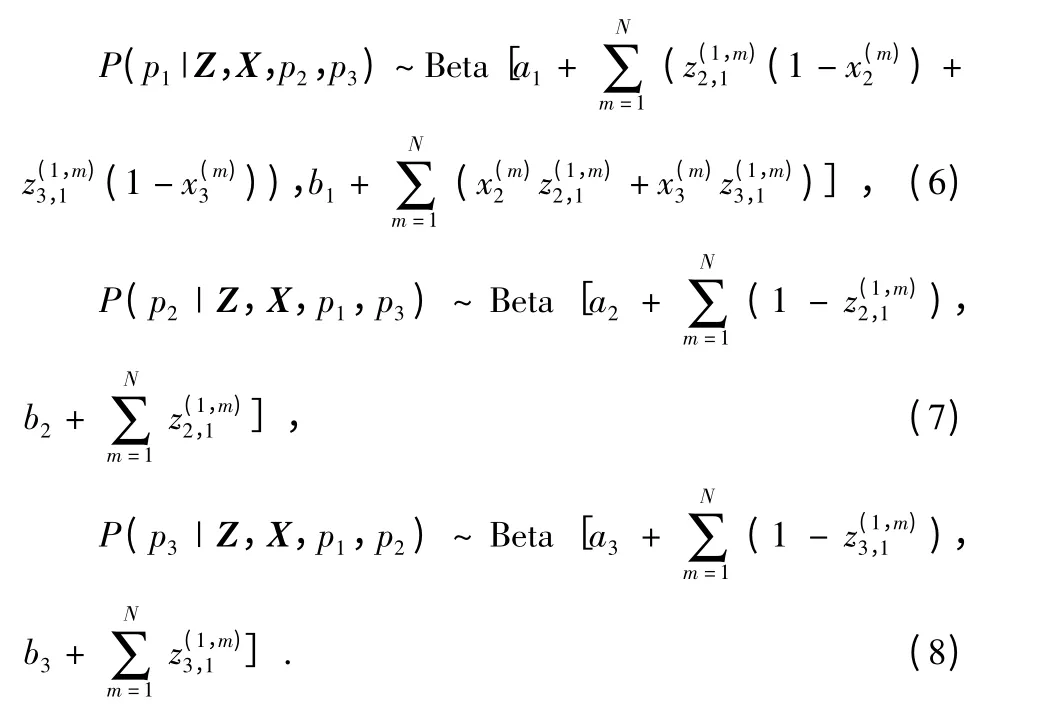
根据后验概率分布式(6)～式(8)，用Gibbs 抽样方法连续抽样，就可得到{p1，p2，p3}和{z2，1，z3，1，z4，1}的抽样数据，就可以利用式(9)计算{p1，p2，p3}的估计值

同理，可以完成对{q1，q2，q3}的计算。

2.2 算法描述

将算法扩展到一般网络中，数据共采集J=J0+J1次，J0是到达稳态所需数据收集次数。算法首先依据先验概率分布抽取Θ(0)和Z(0)，然后利用测量值抽取Θ 和Z 并计算详细描述如下:

Initialization:Draw random samplesΘ(0)and Y(0)from theirprior.

Sample:for j=1，2，…，J do

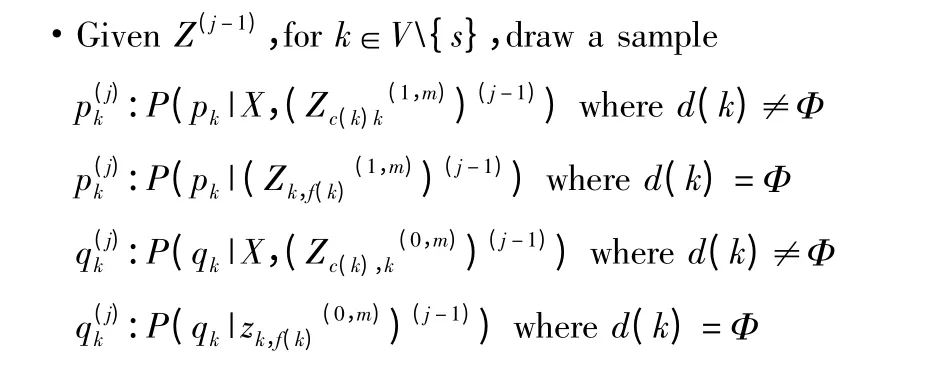
·GivenΘ(j)，for k∈V{s}，for m=1，2，…，N，draw a sample

3 仿真实验

用NS2［7］模拟传感器网络数据汇聚过程，链路报文丢失率(p，q)预先设定。仿真中采用两种网络拓扑结构，9 节点网络现150 节点网络，分别验证算法准确性和可扩展性。每种拓扑结构下分别模拟两种场景下的报文丢失情况:无丢失严重链路和有丢失严重链路。正常链路丢失率设置为(10%，85%)，丢失严重链路为(15%，80%)。

9 节点网络仿真结果如图2～图5 所示，从图2，图3 中可以看出:无丢失严重链路场景中，丢失率推测值和预设值非常接近;在有丢失链路场景中，预设值和推测值同样较为吻合，但靠近叶子节点的推测值误差稍大，其主要原因是将在父节点丢失的报文归结于子节点发送丢失。总体来说，其推测误差都在1%内，说明算法可以较好地完成链路丢失率推测。

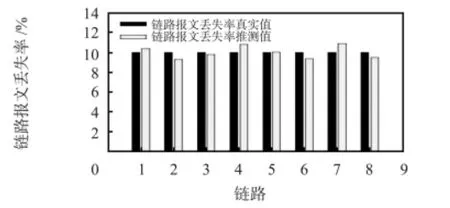
图2 无丢失严重链路:预先设置参数p 与推测值p 的比较Fig 2 No heavy loss link scenarios:ture loss rate p vs inferred loss rate p

图3 无丢失严重链路:预先设置参数q 与推测值q 的比较Fig 3 No heavy loss link scenarios:ture loss rate q vs inferred loss rate q

图4 有丢失严重链路:预先设置参数p 与推测值p 的比较Fig 4 Heavy loss link scenarios:ture loss rate p vs inferred loss rate p

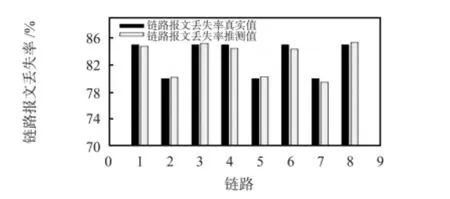
图5 有丢失严重链路:预先设置参数q 与推测值q 的比较Fig 5 Heavy loss link scenarios:ture loss rate q vs inferred loss rate q

表1 是150 节点网络拓扑的仿真结果，从表中可以看出:随着网络规模的扩大，推测误差并没有呈几何级数增加，推测值依然很接近预设值。在仿真过程中，误差的最大值仍然小于1%。说明算法的可伸缩性较好，推测值的误差值不会随着网络规模的增加而变大。

4 结 论

本文提出一种传感器网络链路时间相关丢失率推测算法，将传感器网络逻辑链路报文丢失推测问题形式化为Bayesian 推测问题，并采用Gibbs 抽样方法来解决。采用NS2 仿真工具进行算法的有效性和可伸缩性验证，结果表明:算法可较准确地推测出链路报文丢失率，且伸缩性较好。

表1 150 节点网络拓扑的仿真结果Tab 1 Simulation result of 150-node network topology

［1］ Shah－Mansouri V，Wong S.Link loss inference in wireless sensor networks with randomized network coding［C］∥Global Telecommunications Conference(GLOBECOM 2010)，Miami，Florida，USA:IEEE，2010:1－6.

［2］ Yu Yang，Xu Yongjun，Li Xiaowei，et al.A loss inference algorithm for wireless sensor networks to improve data reliability of digital ecosystems［J］.IEEE Transactions on Industrial Electronics，2011，58(6):2126－2137.

［3］ J Wenli，G Teng，J Meiyin，et al.Researching topology inference based on end－to－end date in wireless sensor networks［C］∥2011 International Conference o Intelligent Computation Technology and Automation(ICICTA)，Changsha，China:IEEE，2011:683－686.

［4］ Y Xunqi，W Modestino，T Xusheng.The accuracy of Gilbert models in predicting packet－loss statistics for a single－multiplexer network model［C］∥INFOCOM 24th Annual Joint Conference of the IEEE Computer and Communications Societies，Miami，FL，USA:IEEE，2005:2602－2612.

［5］ Hartl G，Li Baochun.Loss inference in wireless sensor networks based on data aggregation［C］∥Third International Symposium on Information Processing in Sensor Networks，Berkeley，California，USA:IEEE，2005:396－404.

［6］ Yu Yang，Xu Yongjun，Li Xiaowei.Topology tomography in wireless sensor networks based on data aggregation［C］∥International Conference on Communications and Mobile Computing，Leipzig，Germany:IEEE，2009:37－41.

［7］ The network simulator NS－2［DB/OL］.［2011—11—05］.http:∥www.isi.edu/nsnam/ns/.