基于风向标的光纤Bragg 光栅风向仪设计

胡 威，李英娜，赵振刚，谢 涛，张长胜，李 川

(昆明理工大学 信息工程与自动化学院，云南 昆明650500)

0 引 言

在风力发电领域，无论是风电场的选址，还是风力机的功率特性研究和风力发电机组的功率控制，应用风向仪对风向进行测量均是其重要环节［1～3］。目前风向测量最常用的方法［4～6］主要有以下几种:第一种就是应用机械式风向传感器进行测量，其以单板风向标作为感应元件，信号转换方式主要包括格雷码盘和电位器。格雷码盘转换原理为风向标随着气流的运动而运动，风向轴带动格雷码盘与风向标同时转动，从而输出格雷码信号，将机械位置信号转换成电信号。之后出现了在机械式的基础上加上旋转台，旋转台时钟指向风向，通过计算齿轮的角度可以计算出风向［7，8］。第二种方法就是应用超声波测风仪［9～11］测量风向方法，其采用超声波探头摆成三角形状，利用超声波各个接收探头间的顺风与逆风时间差进行计算得到风向。另外还有一些新的方法，例如:有人研究利用仿生学原理［12］的触须传感器来测量风向，这种传感器灵敏度高，结构简单，造价低廉。

本文设计了一种基于风向标的光纤Bragg 光栅(FBG)风向仪，并对风向仪进行了风洞测试。

1 FBG 风向仪的结构与测量原理

FBG 风向仪主要部件包括:风向标主体、方向凸轮、角度凸轮、等强度悬臂梁等。FBG 风向仪的结构示意图见图1所示。

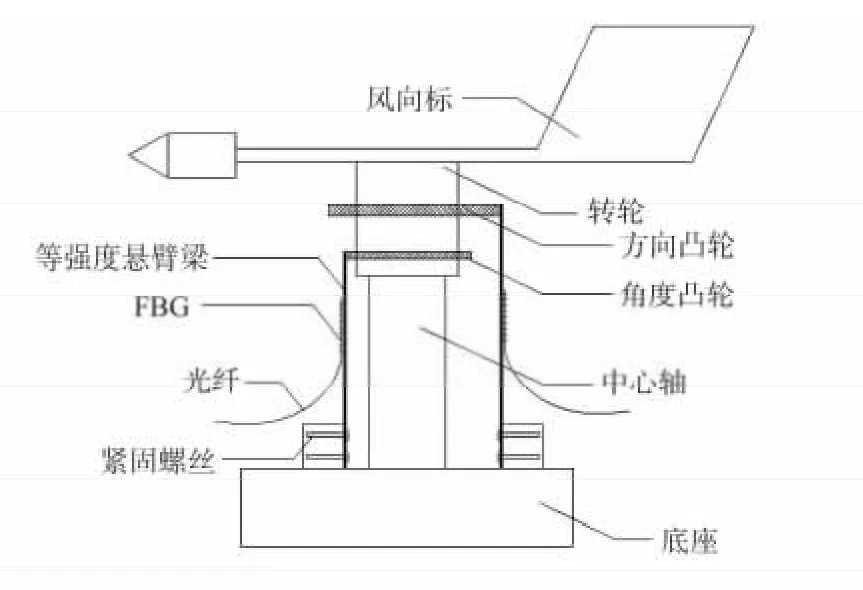
图1 FBG 风向仪结构示意图Fig 1 Structure diagram of FBG dogvane

它的工作原理是当风向改变时，风向标受风力发生旋转，风向标转轮的转动带动方向凸轮和角度凸轮旋转一定角度，角度凸轮突出部分撞击等强度悬臂梁使其产生挠度变化，进而导致粘贴在等强度悬臂梁表面中心轴线上的FBG 中心波长发生移位［13］。在角度凸轮对称轴一侧的180°范围内，经过计算，可以得出风向标旋转角度α 与FBG的中心波长移位量呈线性关系。因此，根据Bragg 光栅中心波长移位量可得到风向标旋转的角度，配合紧贴方向凸轮的等强度悬臂梁上的Bragg 中心波长是否发生移位就可得知在360°范围内旋转角度，风向标旋转角度即风向改变角度，从而计算出风向，实现对风向进行实时监测。

由FBG 风向传感器的结构可知，在角度凸轮对称轴一侧的180°范围内，当风向改变时，即风向标转轴旋转一定角度，角度凸轮也随之旋转相同的角度。角度凸轮的凸出部分的顶角为θ，凸出部分从顶角沿着两半圆周线性增大。在角度凸轮旋转的过程中，与角度凸轮紧贴的等强度悬臂梁就会因为角度凸轮凸出的部分而产生一定的扰度，从而导致粘贴在等强度悬臂梁外表面中心线处的FBG 产生波长移位［14］。当风向改变角度为α 时，即风向标旋转角度为α，角度凸轮也随之旋转相同的角度α，等强度悬臂梁所产生的扰度h 为

式中 θ 为角度凸轮凸出部分的顶角，r3为角度凸轮圆弧部分的半径。等强度悬臂梁所受的应变量ε 为

式中 hb为等强度悬臂梁的厚度，l 为等强度悬臂梁的长度。将式(1)代入式(2)得

而FBG 波长位移与等强度悬臂梁自由端应变关系公式可表示为

式中 Pe为光纤的有效弹—光系数，λB为FBG 的中心波长。将式(3)代人式(4)得

在角度凸轮对称轴一侧的180°范围内，根据式(5)可以得出风向标旋转角度α 与FBG 的Bragg 中心波长移位量ΔλB呈线性关系。

由FBG 风向传感器的数学模型，FBG 的Bragg 波长移位对风向标旋转角度α 的响应灵敏度为

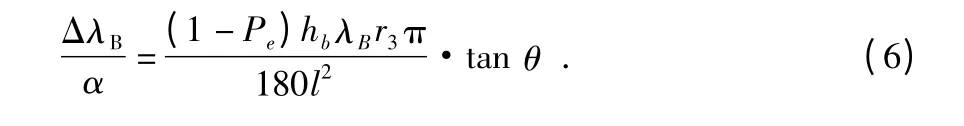
对FBG 风向传感器整装时，首先将方向凸轮和角度凸轮安装于风向标主体的转轮部分，再将等强度悬臂梁固定在底座上，将风向标主体安装在底座上。风向传感器的整装实物图与其主要元件实物图分别见图2 与图3 所示。

图2 风向传感器的实物图Fig 2 Physical map of wind direction sensor

图3 风向传感器的主要元件实物图Fig 3 Physical map of main elements of wind direction sensor

2 FBG 风向仪的风洞测试

在整装完FBG 风向传感器之后，把测试平台所需的其他器件组装起来，进行风向测试实验。测试系统由风洞、调速系统、FBG 风向传感器、数据采集装置(宽带光源、光谱分析仪)组成。风向传感器测试实验原理图见图4 所示。

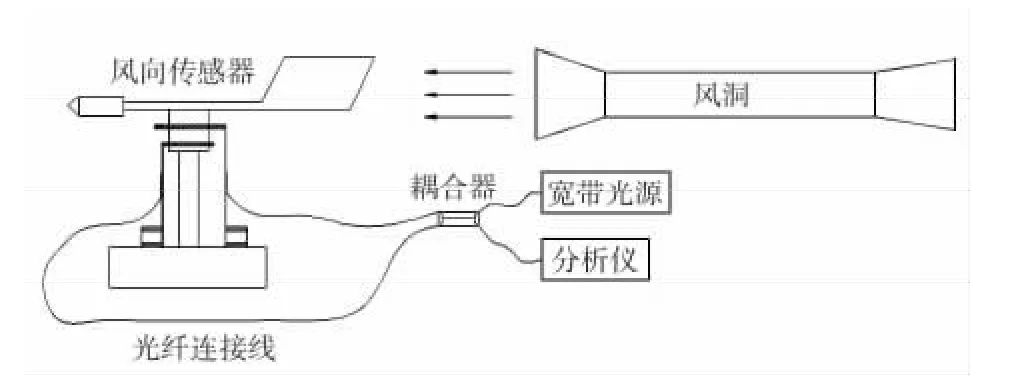
图4 风向传感器测试实验原理图Fig 4 Testing experimental principle diagram of wind direction sensor

当风洞开启时，风洞出风口能够保持均匀稳定的风速，其对风向标产生扭力矩，进而调节风向。实验时将光栅的中心波长移位信号传送至光谱分析仪，将光谱分析连至计算机，经计算机进行数据处理，通过软件显示出光栅的中心波长值可得到风向标旋转的角度。配合紧贴方向凸轮的等强度悬臂梁上的Bragg 中心波长是否发生移位就可得知风向标旋转角度(在360°范围内)，即风向改变角度，从而确定出风向。

在对风向传感器测试实验前，要对FBG 风向传感器的灵敏阈即起动风速进行测定，经过测定当风速小于1.2 m/s时，风向标无法旋转完整一周，这是由于角度凸轮和方向凸轮与等强度悬臂梁之间存在一定摩擦力，在风速较低时，风向标所受压力小于最大摩擦力，风向标无法旋转完整一周，因此，FBG 风向传感器的启动风速为1.2 m/s。

在该测试实验中，传感器要测量各个方向，首先将FBG风向传感器固定在一个位置，并记这个位置为起始位置(通常把起始位置记为0°)，风向标在没有发生旋转时，记录FBG 的初始中心波长。然后改变风洞的方位来调整风向标的旋转角度为30°时，系统稳定后记录下FBG 的中心波长值。重复上述步骤，每次将风向标的旋转角度调高30°，系统稳定后记录下FBG 的中心波长值。直到风向标旋转一周，即旋转角度为360°，记录下最后FBG 的中心波长值。

为了更加方便直观地展示实验中系统得到的大量数据，在每次实验时，建立二维坐标，其中以风向标旋转的角度即风向改变的角度为x 轴，相应的，FBG 中心波长值为y 轴。记紧贴角度凸轮的等强度悬臂梁上的FBG 为FBG1，紧贴方向凸轮的等强度悬臂梁上的FBG 为FBG2。

5 次测试实验FBG1 的中心波长移位量平均值与平均值曲线分别参见表1。5 次测试实验FBG2 的中心波长移位量平均值与平均值曲线分别参见表2。

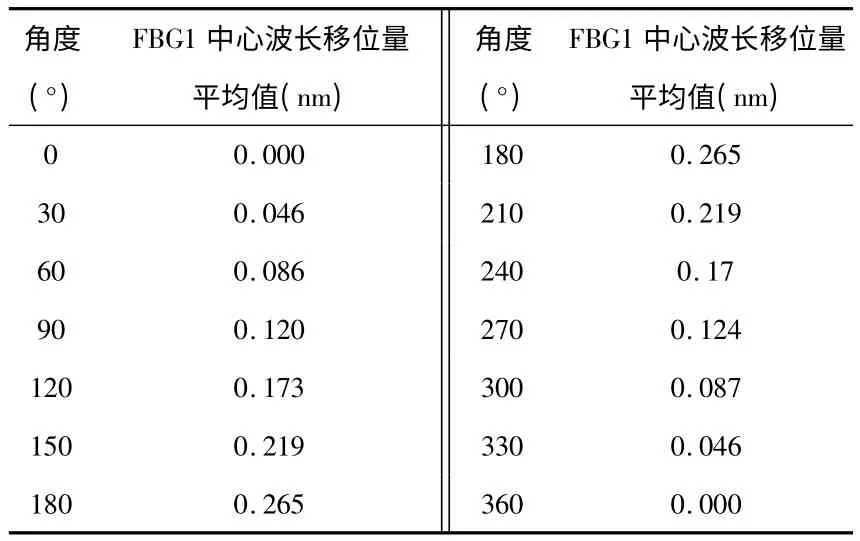
表1 5 次测试实验FBG1 的中心波长移位量平均值Tab 1 Average value of FBG1 center wavelength shifting amount of five testing experiments

通过对FBG 风向传感器5 次实验数据表明:当风向标旋转角度从0°～180°时(0°＜α ＜180°)，紧贴角度凸轮的等强度悬臂梁上的FBG1 的中心波长值逐渐变大，紧贴方向凸轮的等强度悬臂梁上的FBG2 的中心波长值发生移位。当风向标旋转角度从180°～360°时(180°≤α ≤360°)，紧贴角度凸轮的等强度悬臂梁上的FBG1 的中心波长值逐渐变小，紧贴方向凸轮的等强度悬臂梁上的FBG2的中心波长值没有发生移位。这与FBG 风向传感器的测量原理相符合。根据中心波长移位量与角度关系，经计算得到当度数在0°～180°时拟合曲线方程为:y=0.001 4 x－0.0017，当度数在180°～360°时，拟合曲线方程为方程y=－0.001 4 x+0.5236。拟合数据与实验数据最大偏差分别为:当旋转角度为180°时为0.015 nm;当旋转角度为270°时为0.021 nm，由此算得系统非线性度分别为5.66%FS和7.92% FS，因此，FBG 风向传感器的非线性误差为7.92%FS。对多次测量数据分析得到系统灵敏度为1.47 pm/(°)，重复性误差为6.03%FS。

3 结 论

本文应用一种基于风向标的FBG 风向仪来对风向进行监测，在FBG 传感器的风洞实验中，记录光栅中心波长随风向标旋转角度变化的情况，根据实验所得数据得到中心波长变化与风向的关系。风洞实验表明:起动风速为1.2 m/s，非线性误差为7.92%FS，灵敏度为1.47 pm/(°)，重复性误差为6.03%FS。

［1］ 陈 达，张 玮.风能利用和研究综述［J］.节能技术，2007，25(4):339－359.

［2］ 张国伟，龚光彩，吴 治.风能利用的现状及展望［J］.节能技术，2007，25(1):71－76.

［3］ 蒋东翔，洪良友，黄 乾，等.风力机状态监测与故障诊断技术研究［J］.电网与清洁能源，2008，24(3):40－44.

［4］ 施德藩.高动态性能测风传感器的研制［J］.气象水文海洋仪器，1999(1):16－22.

［5］ 刘艳华，李富余，张宏升，等.超风速仪与三轴风速仪测风的比较研究［J］.气象水文海洋仪器，2003(3):7－16.

［6］ 彭 艳，张宏什，许 飞，等.风杯风速计测风误差的分析研究与订正方法［J］.气象水文海洋仪器，2003(2):1－11.

［7］ 陈 梅，洪 飞，李 鑫，等.风速风向传感器在风机控制中的应用于研究［J］.自动化技术与应用，2008，27(4):38－41.

［8］ Piotto M，Bruschi P，Butti F，et al.2D anemometer based on multichannel single chip flow sensor［M］.Berlin:Springer Netherlands，2010.

［9］ 金 晶，唐慧强.基于ARM 的超声波风速测量系统［J］.仪表技术与传感器，2009(6):101－106.

［10］Hall James S.Electrical perpendicular fluid flow measurement with a spatial array of ultrasonic transducers［C］∥Proceedings of IEEE International Ultrasonics Symposium，2009:741－744.

［11］Michael Unser，Dimitri Van De Ville.The pairing of a wavelet basis with a mildly redundant analysis via subband regression［J］.IEEE Transactions on Image Processing，2008，17(11):2040－2053.

［12］项甫根，谷 安，章 勇.基于触须传感器的风速测量研究［J］.自动化仪表，2008，29(9):47－49

［13］李 川.光纤传感器技术［M］.北京:科学出版社，2012.

［14］李 伟.双悬臂梁式光纤Bragg 光栅位移传感器［D］.昆明:昆明理工大学，2010.