GNSS 姿态测量接收机性能分析

敖 翔，崔晓伟，吕 鹏，刘 刚

(1.清华大学 电子工程系，北京100084;2.空军装备研究院通信所，北京100085;3.清华大学 精密仪器系，北京100084;4.海军航空工程学院 控制工程系，山东 烟台264001)

0 引 言

利用全球导航卫星系统(global navigation satellite system，GNSS)信号进行姿态测量是通过载波相位差分算法计算出载体上两个或多个天线之间的相对位置，然后转换为姿态角。目前已有利用多个独立GNSS OEM 板卡对各个天线的信号分别处理以提取载波相位观测值，然后通过差分算法计算出载体姿态角。这种方式分离了各天线之间的时间相关性和运动相关性，降低了系统整体性能。基于上述考虑，部分学者［1～3］提出了同源射频平台利用各射频通路之间的相关性，以实现性能更优越的姿态测量算法。

本文基于同源射频平台设计实现了姿态测量接收机，同时对其进行性能分析。

1 姿态测量接收机

1.1 接收机射频

同源射频下姿态测量接收机利用同一频率对各个天线的信号进行下变频处理，使用相同模型滤波器和AD 采样。接收机射频结构［2］如图1 所示。

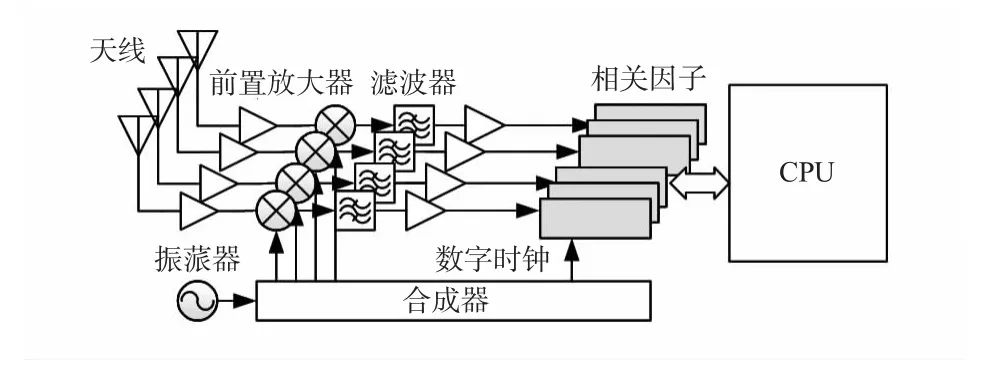
图1 接收机射频结构Fig 1 Receiver RF structure

考虑单颗卫星发射的某一频点的信号，则GNSS 卫星L1 载波上的测距信号表示为

下变频混频滤波后信号为

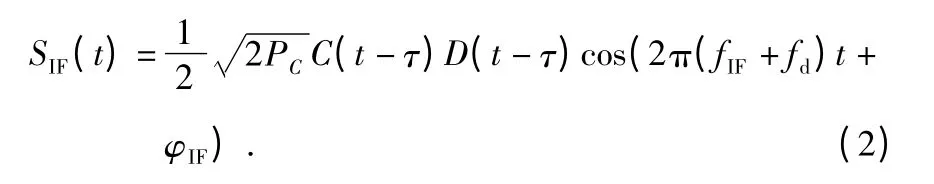
由于GNSS 信号功率相当微弱，在基带信号处理时需要进行相干积分操作，提高环路工作的信噪比。各射频通路预检测积分结果表示为

其中，k 为第k 路射频通路;Tc为相干积分时长;C/N0为信号载噪比;Δfk为接收与本地信号的多普勒频率差;Δφk为接收与本地信号的相位差;R 为扩频信号的自相关函数;D 为当前导航电文符号;η 为相干积分噪声［4］。

1.2 模型分析

同源GNSS 姿态测量接收机将射频分为主射频通路和从射频通路，预检测积分向量可以表示为

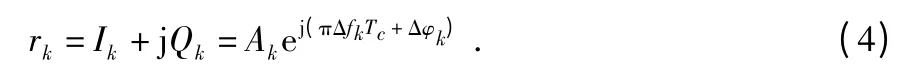
将主射频通道预检测积分向量r1与从射频通道预检测积分向量r2的共轭进行相乘，可得载波相位差分观测值

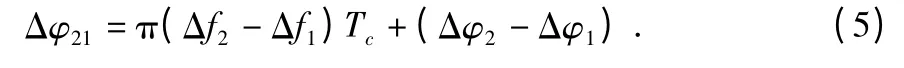
差分相位表示为

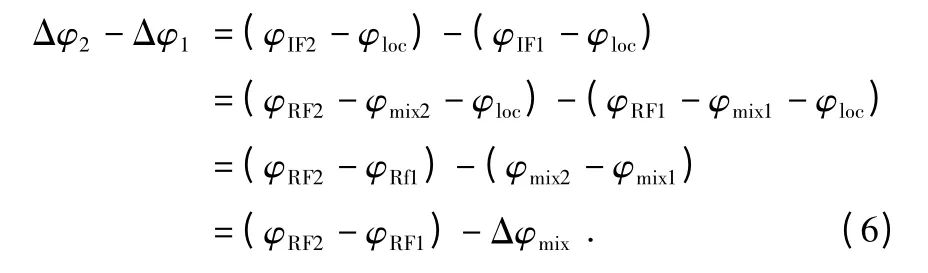
差分载波多普勒表示为

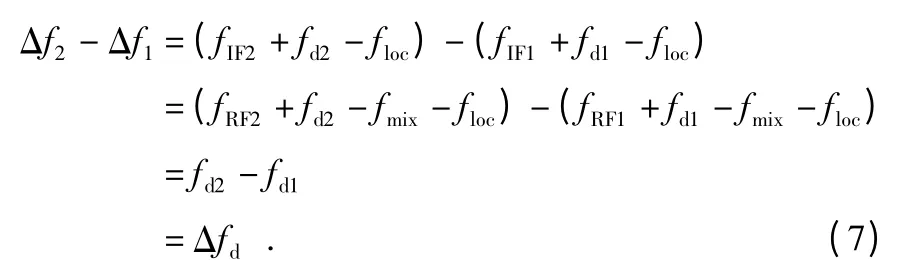
其中，Δφ 为接收信号与本地信号的相位差;φloc为本地生成的载波相位值;φIF为混频后的相位;φmix为混频器输出的相位;Δφmix为主从射频混频器输出相位常值偏差;fIF为中频频率;fd为相对运动引起的多普勒;floc为本地生成的载波频率;fRF为卫星载波频率;fmix为上变频后的混频频率。

考虑各射频通路输入到混频器的信号线路延迟不同，以及RF 信号处理通路长度不匹配，差分载波相位观测值可以表示为

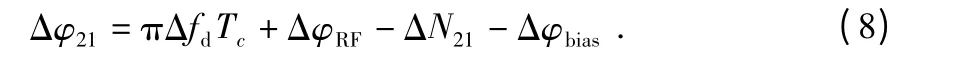
各天线之间的距离绝对偏差值表示为

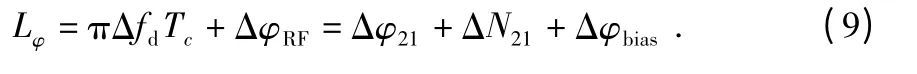
其中，Δfd为多普勒差分量;ΔφRF为相位绝对偏差量;Δφ21为差分观测值;ΔN21为初始模糊度;Δφbias为相位不匹配度。

为了恢复出2 个天线之间的绝对距离量，需要获取3 个观测量(Δφ21，ΔN21，Δφbias)。相位偏差Δφ21是差分相位鉴别器输出结果;初始模糊度ΔN21可通过整数最小二乘方法搜索得出;不匹配度Δφbias和当前工作环境相关。

1.3 观测量提取

传统接收机的全周载波相位观测量输出需要校验当前电文的比特状态，整个过程一般需要2～8 s 时间，若中间有信号丢失，该过程需要重新开始。同源射频平台是通过差分相位鉴别器输出的观测量，主通道和从通道使用相同的晶振和本地载波及伪码。差分相位鉴别值与本地载波频率及相位无关，载波相位测量值的提取独立于主通道环路。当环路判断捕获到信号后，调整环路将频率和伪码到正确的频点和码相位处，该过程一般只需50 ms 即可输出全周差分载波相位观测量。

2 基线解算

2.1 基线解算模型

同源射频下姿态测量接收机中输出的原始观测量为同一卫星不同天线之间的差分载波相位。以主天线第1 路射频坐标作为线性化起始点，可得站间差分的线性观测方程，可以将观测方程写成矩阵的形式

其中，Lφ为线性化后载波观测向量;A 为卫星观测矩阵;X 为基线向量;B 为模糊度系数矩阵;N 为卫星模糊度;Lbias为射频通路相位偏差值向量，各颗卫星为相同值Δφbias。

若当前载体的基线向量X 已知，则当前卫星的模糊度参数方程可以写为

若当前载体的模糊度N 已知，Lbias可以作为基线向量的第4 个参数完成方程的求解，则当前的基线向量和相位偏差值参数方程可以写为

若当前载体的模糊度N 和相位偏差值Δφbias已知，则当前的基线向量参数方程可以写为

同源射频下姿态测量接收机在基线解算过程中需要经历3 个过程:首先根据观测方程建立双差定位模型，计算当前基线向量和双差模糊度［5，6］;然后根据方程(11)反算出单差模糊度和相位偏差值;最后根据方程(12)设计滤波器完成基线向量和当前相位偏差值求解。

2.2 基线滤波方程

独立接收机相位观测是通过对信号锁相跟踪实现，相位精度同锁定状态相关。同源姿态测量接收机相位观测值提取独立于主通道跟踪环路，可以设计单颗卫星的矢量卡尔曼滤波器同时完成对观测量的平滑和基线滤波估计。基线向量设为匀速模型;载波相位偏差设为一阶随机游走模型［7，8］。

卡尔曼滤波状态方程为

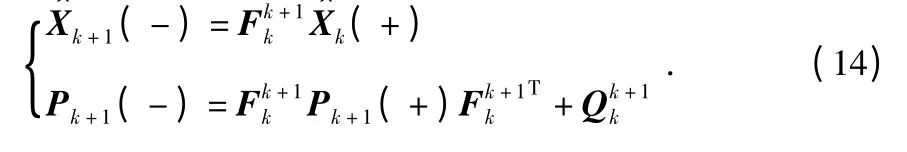
状态向量

状态转换矩阵

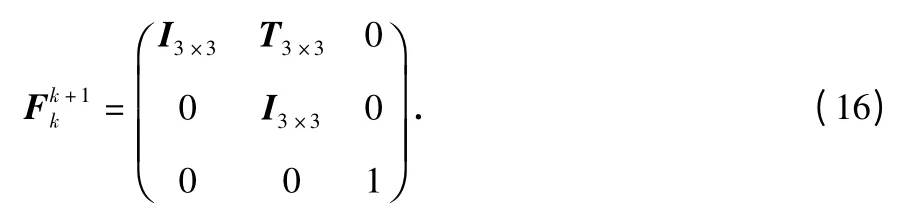
其中，rT为基线向量;vT为基线向量的变化率(转速);λφbias为相位偏差。

卡尔曼滤波测量方程为

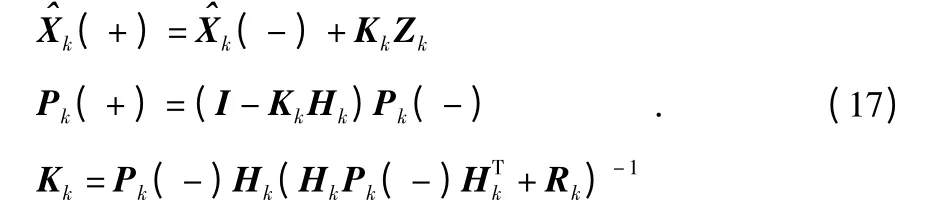
差分载波相位观测值更新矩阵

其中，n 为卫星数;An×3为卫星观测矩阵;1n×1为单位向量。

测量新息向量Zk是由各卫星提取出的差分载波相位观测值Δφ 计算得到

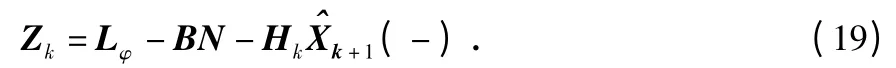
其中，Lφ为线性化后的观测向量(由差分载波相位观测值计算得到);B 为模糊度系数矩阵;N 为单星整周模糊度。

测量更新方程中可以引入基线向量长度信息

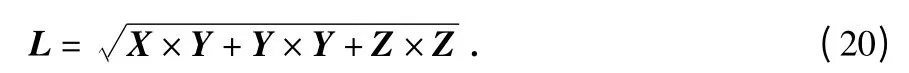
基线向量长度约束方程表示为长度信息对基线向量速度的约束。方程在卡尔曼滤波状态更新时刻进行线性化可得测量信息量

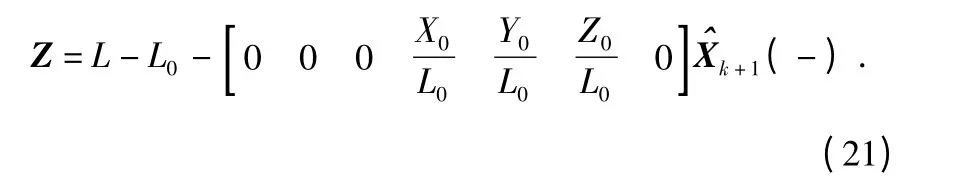
其中，［X0Y0Z0］为基线线性化起始坐标值;L0=为初始长度。

上述卡尔曼滤波算法的测量更新数据源为各通道1 ms差分载波相位观测值和基线向量长度约束方程，此时计算资源开销非常大，需要优化卡尔曼滤波器的速度。卡尔曼滤波5 方程对观测值和系统状态处理的方程只有2 个，剩下3 个方程是计算当前卫星对信息处理过程中的权重值。考虑到GNSS 接收机中处理卫星信号的变化速度相对于1 ms积分时间而言较慢，权重矩阵的计算周期使用10 ms。为了保持整个滤波过程中的精度，其观测值和系统状态处理仍保留1 ms 处理周期。相比于标准的卡尔曼滤波方程，这里只降低了较少的模型精度和测量精度，而获取到了较快的处理速度。

2.3 系统性能分析

利用GNSS 接收机确定载体姿态误差源主要来自于载波相位测量噪声。对于独立接收机搭建的姿态测量系统，各天线的运动和各板卡中晶体动态，直接影响到了各接收机的载波相位测量值，进而影响姿态测量结果。对于同源GNSS 姿态测量接收机，天线的运动和各板卡中晶体动态过程中的共模分量在相位鉴别器提取信号过程中已经消除，原始观测量中的信号动态应力最小，因而，在信号提取模型上，同源平台下的观测量高于独立平台。同时基于基线向量的矢量卡尔曼滤波器的滤波模型能准确地反映出当前载体向量的动态过程，因而，航向角测量精度理论上高于独立接收机搭建的姿态测量系统。

3 对比实验分析

对比实验中同源GNSS 姿态测量接收机使用2 路由MAX2769 构成的射频电路，同时有两台Novatel 接收机同步采集数据用于对比分析。考虑到同源平台下具备多种数据处理算法和各种场景下的角度测量性能，这里对比分析四种方法下的角度测量结果:

1)独立平台Novatel 接收机;

2)同源平台按独立接收机处理;

3)同源平台矢量滤波器;

4)同源平台矢量滤波器仅3 颗卫星。

如图2，实验车顶设备离主天线(后)大概距离为:Novatel 天线113 cm;IMU 设备170 cm;辅天线(前)237 cm。IMU1为组合导航系统用于其它功能测试，IMU2 为独立惯性导航系统，与姿态测量接收机同步采集数据，用于事后同姿态测量接收机对比分析。

图2 实验车平台Fig 2 Platform of experimental car

跑车实验主要在停车场上完成，观测环境良好，整个时段大部分可以观测8～9 颗卫星，其中7 颗卫星的载噪比在44 dBHz 以上;之后进行路测，可见卫星一般为6 颗，部分路段有高楼遮挡时可见卫星只有4 颗，偶尔有车辆从旁边经过时只有2～3 颗可见卫星。跑车实验过程可以分为3 个时段:

1)先顺时针绕圈用来模拟低动态场景;

2)然后绕8 字轨迹用来模拟中等动态场景;

3)最后出停车场进行路测。

实验车上有3 套系统可以计算当前方向角:独立平台Novatel 天线与主天线;同源平台辅天线与主天线;RTK 轨迹同IMU2 组合导航。分析中需要考虑到独立平台基线长度约是同源平台基线长度的50%的影响。首先按照本文提到的四种方法处理卫星观测数据获得角度测量结果。

方法3 输出的航向角精度理论上最高，因而，在对比分析中以方法3 输出角度作为基准，其它方法得到的航向角都与之做差(图3)。

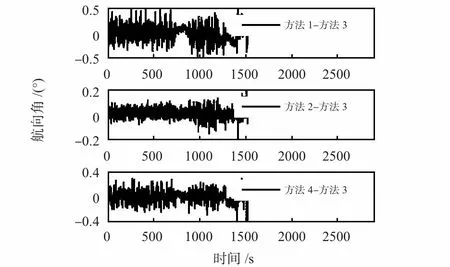
图3 卫导相对方法3 航向角差值Fig 3 Difference of heading angle by relative method 3

由表1 知，方法1 和方法3 之间的航向角差值的标准差为0.15°。从图3 可以看出:动态时段下的噪声比静止时段大，动态时段输出的角度噪声明显比同源平台大。

方法2 和方法3 之间的航向角差值的标准差为0.03°。这一误差主要是由实际动态模型和滤波模型决定。从图3可以看出:低动态场景下的误差小于中等动态下的误差，因此，方法2 和方法3 中有一种方法的滤波模型误差相对而言比较大。文章之前提到方法3 的动态应力比方法2 小，且滤波方程为直接矢量估计更符合运动模型，因而，这里的误差量主要是方法2 引起。

方法4 和方法3 之间的航向角差值的标准差为0.09°。在动态环境中，即使只有3 颗可观测卫星也能输出具有一定精度的航向角。

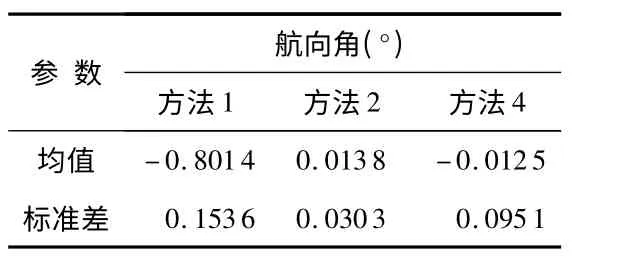
表1 航向角Tab 1 Heading angle

实验车进行路测后由于观测环境不稳定，按照传统数据处理方法无法计算出航向角，而同源平台矢量卡尔曼滤波算法具备在只有3 颗卫星下工作的能力。可以用IMU2组合导航系统计算的航向角与之进行对比验证，惯导IMU2陀螺零偏稳定性为30°/h。组合导航系统利用Novatel 接收机输出观测量进行载波差分定位，获取运动轨迹后同惯导IMU2 进行组合导航。数据采集过程中第1 时段下的惯导原始观测数据不连续，图4 为对比分析第2 时段和第3 时段下相对方法3 的航向角。

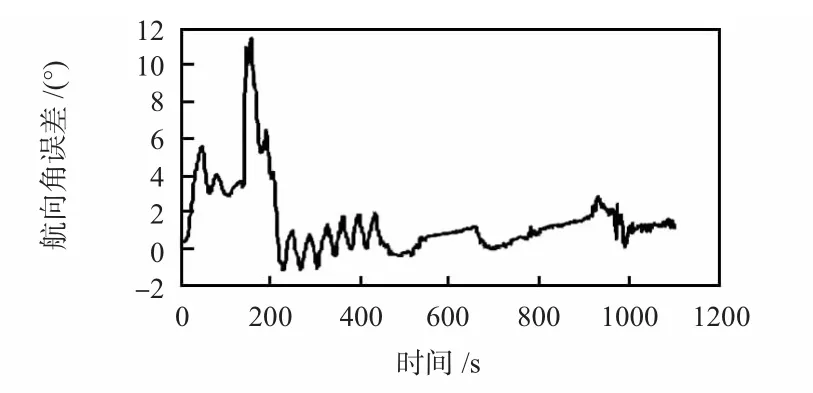
图4 惯导相对方法3 航向角差值Fig 4 Difference of heading angle by relative method 3

IMU 设备同实验车是通过支架加上橡胶锁紧在车顶，设备同实验车之间会有一定的震动偏差，特别是在转弯过程中两系统会有角度偏差。从最终的对比结果可以看出:信号较好时转弯过程中会引入周期性的系统不一致性偏差，整体测量噪声很平滑;静止时断下IMU 系统输出的航向角有漂移，2 min 约0.8°;路测时段中航向角噪声变大，但仍然保持在一定的精度范围内。

4 结 论

当观测卫星质量较好时，同源GNSS 姿态测量接收机下的两种算法都优于传统独立接收机平台下的姿态角测量结果。算法处理精度主要和当前实际运动模型与滤波模型相关。当矢量卡尔曼滤波器处理模型同实际向量运动模型相一致时，滤波得到的航向角有模型信息进行约束，具备更高的输出精度;若模型有偏差，滤波得到的方向角精度比同源独立接收机算法低。

当观测卫星质量较差时，同源GNSS 姿态测量接收机可以在3 颗卫星时进行处理。同时由于观测量提取模型不同于独立接收机平台，同源接收机跟踪到信号后可以直接输出有效的载波相位观测值，比独立接收机平台具有更强的环境适应能力。

［1］ Parkinson B W，Jr J J S.Global positioning system:Theory and application［M］.2nd ed，Washington，DC:American Institute of Aeronautics and Astronautics，Inc，2006.

［2］ Clark Emerson Cohen.Attitude determination using GPS［D］.Stanford:Stanford University，1992.

［3］ Keong J H.GPS/GLONASS attitude determina-tion with a common clock using a single difference approach［C］∥Proceedings of ION-GPS，1999:14-17.

［4］ 周忠谟.易杰军.GPS 卫星测量原理与应用［M］.北京:测绘出版社，1997.

［5］ Teunissen P J G.Least-squares estimation of the integer GPS ambiguities［C］∥Invited lecture，section IV:theory and methodology，IAG General Meeting，Beijing，China，1993.

［6］ Buist P.The baseline constrained LAMBDA method for single epoch，single frequency attitude determination applications［C］∥Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation(ION GNSS 2007)，2001:2962-2973.

［7］ Bishop G，Welch G.An introduction to the Kalman filter［J］.Proc of SIGGRAPH，Course，2001，8:27599-3175.

［8］ Fujikawa S J，Zimbelman D F.Spacecraft atti-tude determination by Kalman filtering of global positioning system signals［J］.Journal of Guidance，Control，and Dynamics，1995，18(6):1365-1371.