基于自动抑制的传感器欠采样CT 影像降噪方法

高 华，傅德胜，李潇阳

(1.南京信息工程大学 计算机与软件学院，江苏 南京210044;2.南京信息工程大学 环境科学与工程学院，江苏 南京210044)

0 引 言

现今，CT 扫描已被作为一种常见诊疗手段而得到广泛应用，但相比其他X 射线检查它既有优点也有明显缺点。其中，CT 的大量辐射问题是最为突出的，因此，国内外研究者都在研究如何有效降低CT 的扫描辐射剂量。实际使用中，医疗工作者主要通过降低X 射线管的电压或者管电流来达到降低辐射剂量的目的，但这会使重建后的影像具有较低的信噪比，严重影响了诊断。

目前研究者已经提出了很多方法有效降低患者的受辐射剂量，主要有三方面研究重点:加快硬件扫描速度、采用感兴趣区域扫描和稀疏重建、低剂量CT 扫描降噪重建。

第一类加快硬件扫描速度是各大厂商研究的重点，例如:目前推出的双源螺旋多层扫描等［1］，其主要方式是提高单位时间内扫描的速度，间接缩短时间从而降低辐射剂量。第二类是目前刚兴起的研究领域，它主要是通过稀疏数据进行数学重建。因为采用了局部感兴趣和稀疏采样降低了辐射剂量［2］，典型算法有基于CS 压缩感知［3］的稀疏重建和欠采样的ROI 重建［4］。第三类是使用降低扫描电流或管电压的方式获得的低辐射投影数据［5］，并在此基础上采用一些算法降噪重建，典型算法如:PWLS［6］、投影域像素降噪［7］、TV 正则降噪等算法［8］。

这些方法都取得了较高的信噪比，但是目前第一类方法进展缓慢，第二类算法仍处起步阶段，而第三类虽研究较早但实际应用不多。这主要是因为第三类算法运算开销较大，且有部分需要经验设置。

本文提出了一种基于投影域数据分析抑制的改进的自适应算法，目的是纠正由传感器老化和欠采样等造成的严重噪声，在其抑制过程中自动修正抑制参数并提高其抑制效果，实验结果表明:该算法抑制噪声取得了较好的效果。

1 噪声分析与模型

CT 噪声主要由2 个方面造成:1)机械产生的噪声，包括了震动、传感器老化等，这一类是无法避免的;2)人工修改机器参数，导致传感器发生光子饥饿。早先国内学者卢宏冰等人［9］采用固定角度多次扫描数据，并分析其统计特性，发现其校正和对数变换后的数据近似服从加性噪声式(1)污染且满足式(2)的总体非线性非平稳高斯分布

其中，f 为理想数据，n 为非平稳高斯噪声。

但实际投影数据中经常会有一些数值较高的点，在文献［10］中张元科博士对其进行论述，并且给出了异值点集中区域。但该方法是基于一种肯定假设:即大部分数据是高于并限定在一定的数值范围内，并且假设异值点较为集中在这些区域。图1 给出了示例。

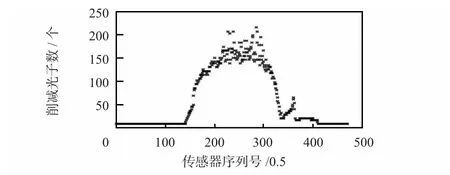
图1 异值点集中区域图形Fig 1 Different values in concentrated area

然而实际数据中也发现，在一些低角度的数据中也会出现异值，分析原因是:X 射线的路径并不完全是直线，即使是在穿透距离较短的情况下仍然会有大量光子跑到其他传感器上，因此，就造成了即使不在异值重点区域也会出现异值的特点;同时也会因为传感器老化而造成光子接受数值有较大偏差，如图2 所示。

因此，在去除明显异噪集中区域的噪声外，也需要对非集中区的异值点进行抑制。而异值点通常是明显高于周边传感器的数值的，而且其在单一方向上的震动幅度是满足一定范围的，因此，这就提供了一个较好的判断依据。

2 算法描述

2.1 算法分析

图2 短穿透投影距离下存在异值Fig 2 Different value exists in short penetrate distance(zoomed area，arrow point to)

为方便检测到异值点，设投影图像为p(x，y)，则g(x，y)为以(x，y)为中心的n×n 窗口，gm(x，y)为窗口均值，则d=g－gm，w(x，y)为窗口内8 领域，t(x，y)为该角度上的投影数据的左右各n+1 方向。示意图如图3 所示。

图3 滤波窗口示例Fig 3 Example of filtering window

选择T1=2σgm，T2=gm，T3=tm，T4=σtm，其中，tm为某角度上的以(x，y)为中心的投影数据条内均值，σgm为窗口内的方差，根据统计学原理，选择2σgm为95%置信区间。由于可能存在期望值相近，为此，再引入标准离差

比较σ1，σ2，σ2，若σ1较小，选择方形窗口内的中值滤波;相反，则选条状区域的均值。

在确定自适应滤波方式后，如何确定异值点，在文献［10］中给出了方法，该方法是一种比较可靠的方法，它为感兴趣的区域设置阈值，按照其规则确认异值点，但该方法需要人工设置参数，且在一些角度上数据全部偏大时进行了过度滤值，并且它是以8 领域方形窗口为主要滤波窗口，这忽略了在单一扫描方向上的数值非平稳连续特性。

本文采用了一种改进的运作方式来判断和更新像素中的异值点，首先相同的就是选择

其中，σ'为两标准离差较小的那个所对应的窗口方差。

然后选择更新图像中的点，不过这里选用了2 个窗口中的数值，其主要目的是进行保守的异值点更新，其更新公式为

在确定异值点后，并更新图像后单角度上的数据更加趋于缓和。处理后结果如图4、图5 所示。

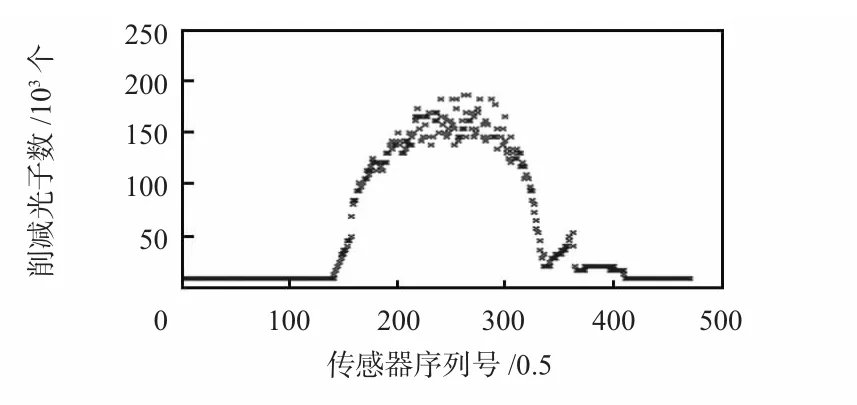
图4 整体抑制Fig 4 Global inhibition

图5 短穿透抑制Fig 5 Short penetration suppression

2.2 算法总结

1)设置窗口大小为3，标准离差和窗口方差、投影方向均值均为0;

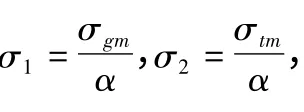
4)重复直至全部扫描完成;

5)更新g(x，y)=g'(x，y);

6)其他经典重建算法重建。

3 实验材料与仿真结果

实验材料选用256×256 的Sheep－Logan 头部，其图形如图6 所示。为了模拟CT 扫描使用扇形束投影fanbeam。旋转角度是180°，984 个采样方向，探测器一共有888 个，探测器距离是1.029 3，X 射线到旋转中心距离是541，中心到探测器的距离是408。在这些参数下仿真出CT 投影数据。

然后利用公式(2)和图6 的数据进行加性噪声的添加，之后，再随机添加异值点，获得低剂量情况下的模拟数据，其中，β 取22 000。

下面给出传统FBP 直接重建［11］、PWLS、以及本文给定的方法滤波后再进行PWLS 方法得到的重建。最后比对重建后与原始图差值，其结果如图7(f)所示。

可以看出，本文使用的方法较好地保存了边缘信息，清晰度比PWLS 要好，但是也发现在下方的3 个连续的椭圆上边缘有模糊，分析结果证明:由于本文算法在缓和投影数据间的差距时，也将一些特别小的物体的投影数据当作是真实数据造成。

图6 Sheep-Logan 模型Fig 6 Sheep-Logan model

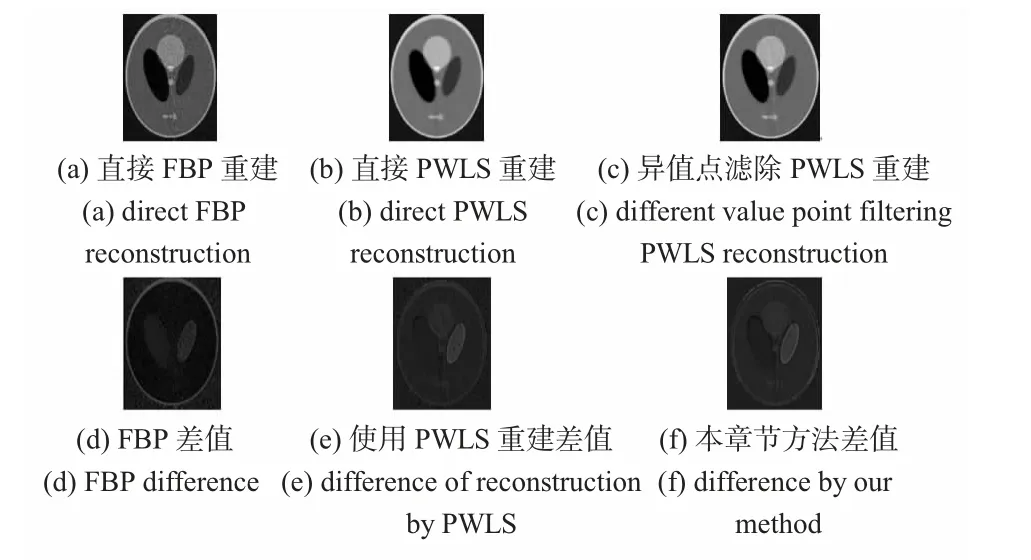
图7 三种方法重建图(a)～(c)，比较差值图(d)～(f)Fig 7 Reconstruction images(show in a～c)，difference value comparison show in d～f use 3 methods

从图7(d)～(f)3 个差值图像可以看出直接FBP 效果(图(d))最差，在其边缘、内部平滑区域都存在严重的噪点，PWLS(图(e))与原始图像差距减小，但也发现其在边缘和在窄边缘发生的复制现象，相比较而言，PWLS 抑制了一部分的内部平滑区域噪声，但在窄地区抑制效果一般。而本文方法可以明显看出，其与原图在内部平滑区域相差不大，但由于其采用直接对投影域数据处理的方法，并没有在后续重建中对边缘进行处理，因此，可以看到边缘的差异。

作为主观判断可以得到一定的结果，但为了更好地表示数据分析的特征，这里引入客观的信噪比分析工具信—噪功率比(PSNR)，其计算公式

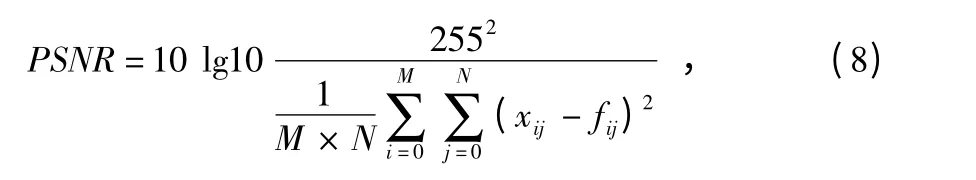
式中 xij为重建后图像，fij为理想图像，M，N 为图像大小，i=1，2，3，…，M;j=1，2，3，…，N;M，N∈Z+，它反映理想图像与处理后图像的信噪比情况。计算结果如表1 所示。

表1 仿真重建后的数据计算PSNRTab 1 PSNR computed by datas after simulation reconstruction

从计算结果与主观判断看，它提高了图像信号所占比例，且图像的质量是可以接受的。

4 结束语

本文分析CT 投影数据的特点，介绍了一些研究成果，提出其不足。分析了投影数据在单角度上的数学特性，发现投影数据去异值点后服从一定的非平稳高斯噪声分布。相邻角度数据相关，且低穿透区域也存在异值，解释了产生的可能原因。在波动较大时，同一投影角度上震动幅度大体相当，并针对该特性提出算法改进，最后进行了仿真实验。实验结果表明:滤除噪声后的数据趋于非平稳高斯分布，重建效果较好，克服了传感器老化等因素，且自动化程度提高，免除了人工设定异值范围的麻烦。

［1］ 张宗军，卢光明.双源CT 及其临床应用［J］.医学研究生学报，2007，20(4):416－418.

［2］ 刘圆圆，张 丽，陈志强.改进的单程分裂合并分割方法在双能CT 欠采样方法中的应用［C］∥全国射线数字成像与CT新技术研讨会论文集，上海:2009.

［3］ 练秋生，郝鹏鹏.基于压缩传感和代数重建法的CT 图像重建［J］.光学技术，2009(3):422－425.

［4］ Xu Q，Mou X Q，Wang G，et al.Statistical interior tomography［J］.IEEE Transactions on Medical Imaging，2011，30(5):1116－1128.

［5］ 朱天照，唐光健，蒋学祥.低剂量螺旋CT 肺结节扫描与常规剂量CT 的对照研究［J］.中华放射学杂志，2004，38(4):428－431.

［6］ Wang Q X，Li H，Lam K Y.Development of a new meshless－point weighted least－squares(PWLS)method for computational mechanics［J］.Computational Mechanics，2005，35(3):170－181.

［7］ 王 旭，陈志强，熊 华，等.联合代数重建算法中基于像素的投影计算方法［J］.核电子学与探测技术，2006，25(6):785－788.

［8］ 张瀚铭，闫 镔，李 磊.一种基于TV 正则化的有限角度CT图像重建算法［C］∥绵阳:全国射线数字成像与CT 新技术研讨会论文集，2012.

［9］ 卢虹冰，李 响，萧颖聪，等.利用K－L 域惩罚加权最小均方平滑对低剂量CT 投影数据进行噪声滤除［J］.中国医学物理学杂志，2002，19(4):200－204.

［10］张元科，张军英，卢虹冰.低剂量CT 投影图像噪声分析及去噪算法研究［J］.光电子.激光，2010，21(7):1073－1078.

［11］钱姗姗，黄 静，马建华，等.基于投影数据非单调性全变分恢复的低剂量CT 重建［J］.电子学报，2011，39(7):1702－1707.