深井似膏体充填管道的输送特性
张钦礼,刘 奇,赵建文,刘贱刚
(中南大学 资源与安全工程学院,长沙 410083)
由于地表及浅部矿体在逐步枯竭,我国矿业发展形势必将由浅部过渡到深部开采。如淮南矿业集团公司的各大煤矿开采深度均已超过800 m,孙村煤矿、金川二矿区、冬瓜山铜矿等矿山的开采深度也已经超过1000 m。充填采矿法是深井开采最主要的采矿方法[1],但由于深井开采,管道从地面铺设到井下时高差较大,充填倍线较小,充填料浆输送时流速较大,料浆高速流动时对管道形成的压力较大,容易导致管道磨损以及堵管、爆管等事故,直接造成系统失效。充填料浆管道输送的性态对充填系统的稳定性研究有非常重要的指导意义。
在浅井矿山,两相流输送有关参数的计算大多参考一些经验公式[2-3],但在深井矿山,对充填料浆管道输送特性的研究还鲜见报道。有研究人员运用数值模拟方法研究稳定流状态下似膏体料浆管输的临界流速问题[4-5];也有通过做环管试验对全尾砂高浓度料浆的输送性能进行研究[6];有人利用毛细管流变仪进行流变试验,对管道远距离自流输送进行研究[7];有人利用Fluent(3D)软件研究粗骨料充填料浆的最佳输送浓度和流速[8]。此外,更多的研究是通过工业试验的方法,根据现场经验来确定充填料浆管道输送的力学参数以及系统的安全性能[9]。这些研究方法均要考虑诸多客观因素,对于较复杂的非线性流动现象的研究不够深入,其研究结果具有一定的局限性,仅仅适合某些特定条件下的管道输送系统,均不能系统、直观地反映在深井管道输送条件下充填浆体的性态,对于超深、超长的充填浆体管道输送系统不具有推广性。
随着计算机技术的飞速发展,为充填料浆管道输送提供了数值模拟的分析方法。目前,用来模拟管道输送的软件,主要有CFX、PHOENICS、ANSYS和FLUENT等。如林金贤等[10]利用CFX软件对直管段和水平弯管中气固两相流的流动阻力特性进行数值模拟;赵会军等[11]利用PHOENICS软件对原油顺序输送混油的模型进行数值求解;陶平凯等[12]利用ANSYS FLOTRAN软件对管道参数进行优化。FLUENT拥有大量的数值模型和科学的数学算法,它主要用于航空航天设计、石油及天然气输送设计、机械设计及涡轮增压设计等方面。在管道输送方面也有诸多研究,如对不定形耐火材料输送管内流动状态进行分析[13];对弯管油水两相流动进行的数值分析[14];对分级尾砂料浆满管流输送技术研究[15];对固-液两相流态充填料浆管道自流输送问题进行研究[16]。但对超深、超长充填管道的研究却很少见。本文作者运用FLUENT软件模拟深井充填管道两相流输送的动力学过程,对浆体输送过程中的主要性态与参数进行定性定量分析,为深井矿山充填系统的设计提供强有力的理论依据和操作性极强的实施方案。
1 似膏体管道输送二维动态模型
本研究是针对某金属矿深井开采充填料浆管道输送系统运行的工程实例进行的。该充填系统属超深、超长似膏体管道自流输送系统。地表与井下高差为735 m,与采场的水平距离为2775 m。该矿的充填工艺是全尾砂似膏体自流充填工艺,充填骨料为尾砂,胶凝材料为水泥,浆体的灰砂比为1:12(质量比),料浆的质量浓度为76%,体积浓度为52%,浆体的密度为1.81 t/m3。
1.1 流变特性数学模型
试验表明,似膏体充填料浆拥有内部结构紧密、初始应力大的特性。按照流变力学理论,它的流变模型比较接近宾汉体模型,验证结果如表1所列。

表1 室内试验验证结果Table 1 Indoor verification results
通过对表1中数据进行回归分析,得出切应力τ和切变率dγ/dt存在线性关系,故此充填料浆的流变模型为宾汉体,其流变模型为

1.2 基本假设和前提
由于矿山浆体输送工艺以及其力学结构极其复杂,所有目前只能获得管道输送问题的近似解而无法求得其精确解。为了方便创建模型以及对其进行求解分析,对所建立的模型做出如下假设:
1)黏性浆体具有恒黏性,不随温度、时间的变化而变化;
2)浆体为宾汉体,看作是不可压缩的;
3)不考虑热交换;
4)不考虑振动、地压波等对管道输送的影响;
5)模拟过程初始管道处于满管流状态。
1.3 模型参数的确定
1)料浆初速度
该矿山充填站的料浆流量为220 m3/h,充填管道内径0.154 m。管道采用的是无缝钢管。料浆入口速度(v)由式(2)计算:

式中:Q为料浆流量,m3/h;D为入口管道内径,m。
计算得到该矿山充填系统料浆初速度为3.28 m/s(按1.05的安全系数取值,这里的料浆初速度取3.4 m/s)。
2)料浆黏度
料浆黏度用NBJ-1D型旋转式黏度计来测定。该仪器由电动机作匀速运动从而带动转子作匀速旋转,并由传感器测量出作用在转子上的黏性阻力,最后经过计算机处理以后可以获得需要测量液体的黏度。经测定,该矿山充填料浆的黏度为0.32 Pa·s。
3)当量粗糙高度及壁面粗糙度系数
料浆输送管道的粗糙程度影响管道阻力,因此,有必要在数值模拟中考虑管道的粗糙度。本文作者模拟似膏体料浆输送的管道是无缝钢管,管壁的当量粗糙高度RS为0.035 mm,代表实际粗糙度。管道的粗糙高度、粗糙形状及其分布都是无规则的,引入壁面粗糙度系数0.14。
4)浆体雷诺数
当雷诺数Re小于2300时,管道内流体的流动状态是层流;当雷诺数Re大于4000时,流动状态是湍流;当雷诺数Re大于2300但又小于4000时,流动状态为过渡状态,流动状态有可能为层流也有可能为湍流,此时的流动状态由外界条件决定。对非牛顿流体在圆管中的流体力学性质,很多学者按照不同的研究目标和研究对象提出很多各不相同的雷诺数定义[17]。本文作者采用基于有效黏度定义的雷诺数公式为

式中:ρ为料浆密度,kg/m3;v为料浆流速,m/s;μ为料浆黏度,Pa·s。
把相关计算参数代入上式,可得Re=2962>2300,在此假定管道输送系统模型处于湍流运动状态。
1.4 二维动态模型
1)二维动态建模
计算所需的几何模型通过GAMBIT专用前处理软件来建立。考虑到充填料浆在管道中输送条件极其复杂以及FLUENT软件在使用条件上的局限性,运用FLUENT软件做定性分析时,管道采用2D平面模型建模,简化图如图1所示。

图1 充填管道几何模型Fig.1 Geometry model of backfilling pipe
管道垂直段长735 m,水平段长2775 m,几何充填倍线3.78,管道内径为0.154 m,采用直角弯管连接,半径为0.45 m。
2)网格的生成
在所建立的模型中,网格的划分质量在很大程度上影响到研究结果的精确性。由于本次模拟的管道长达3510 m,管径为0.154 m,属于超长管道输送。网格划分太密或者太稀疏都有可能加大计算误差。如果网格划分太稀疏会导致计算过程中的离散误差变大,如果网格划分太密将会使得计算过程中的离散点变多,进而导致计算结果中的舍入误差变大。
经多次试验与比较,可以将整个模型分成5部分:进口处、垂直段、弯管处、水平段、出口处。将进口、出口边界均划分为50等份,距进口、出口10 m内管壁边界划分为200等份,弯管垂直和水平各5 m内管壁边界划分为200等份,剩余垂直段划分为7300等份,水平段划分为27700等份,网格数量为702400个。
1.5 边界条件
当模型已经建立,理想的网格也已生成以后,需要对模型的边界进行确定,方便在FLUENT中进一步定义边界条件和初始条件:
1)将入口定义为速度入口(VELOCITY_INLET),并将入口速度设置为3.4 m/s;
2)将出口定义为流动出口(OUTFLOW);
3)将壁面定义为壁面(WALL),壁面粗糙高度(即当量粗糙高度)为35 μm,壁面粗糙度系数为0.14。
由于模型是典型的细长形几何体,因此,应采用双精度解算器进行计算模拟,即采用FLUENT 2ddp进行解算。本次模拟的充填料浆是具有恒定密度的流体,可以看作是不可压缩的,所以,这里选择分离隐式解。同时,考虑到重力的影响,因此,颗粒需要加上重力加速度。
2 结果与分析
2.1 相关变量的残差监测
为了判断计算结果是否收敛,需要监测相关变量的残差值。利用残差值来评判计算收敛与否,对一些常见的问题可能很有效果,但是在一些特殊问题上经常会做出错误的判断。为此,检验计算是否收敛最为有效的方法是不仅要监视残差值以及与变量相关的所有数据,而且要检验模型中流入和流出的物质与能量是否满足守恒定律。
在残差曲线(见图2)中,纵坐标为残差(Residual),横坐标为迭代次数(Iteration number),曲线4为动能(k)。由图2可以看出,虽然在初始阶段模型各变量检测值出现了振荡,但随收敛监测量的逐渐减小,都趋于收敛,迭代计算到1002次后,各变量监测曲线趋于水平,证明模拟结果较为可靠。
2.2 流速分析
当管道为直线段时,料浆沿管道断面存在流速梯度,流速最大处在管道的轴心处,流速分布近似抛物线;当管道为弯曲段时,料浆沿管道截面也有较明显的流速梯度,但流速是由弯管外侧到内侧逐步增加(见图3)。当浆体到达出口位置时,其流动速度会变慢(见图4)。由于重力的作用,水平管道的流速梯度向管壁下侧偏移(见图5)。
管道沿程流速最大值为3.94 m/s,管道流速最大处位于弯管处。水平管段沿程流速最大值为3.74 m/s,根据南非矿山充填的经验,管段的工作流速不宜超过4 m/s,由于管道工作流速越大,对管道磨损率也大大提高。由FLUENT模拟结果可知本研究中管道的工作流速没有超过4 m/s,对管道的磨损是可以接受的,故该矿山充填系统的工作流速是比较理想的。
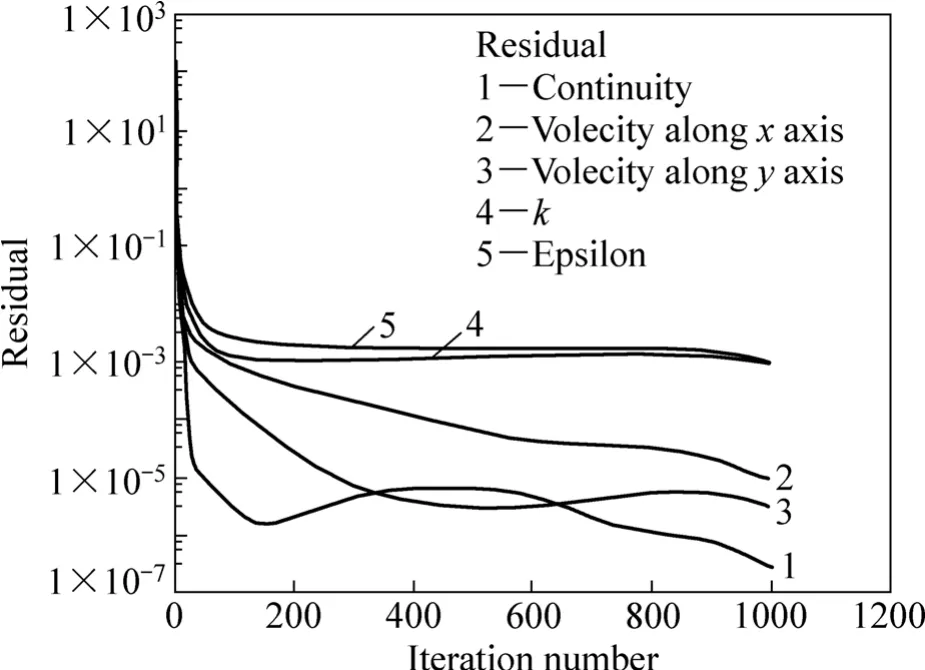
图2 料浆输送残差收敛曲线Fig.2 Residual convergence curves of backfilling slurry at transportation
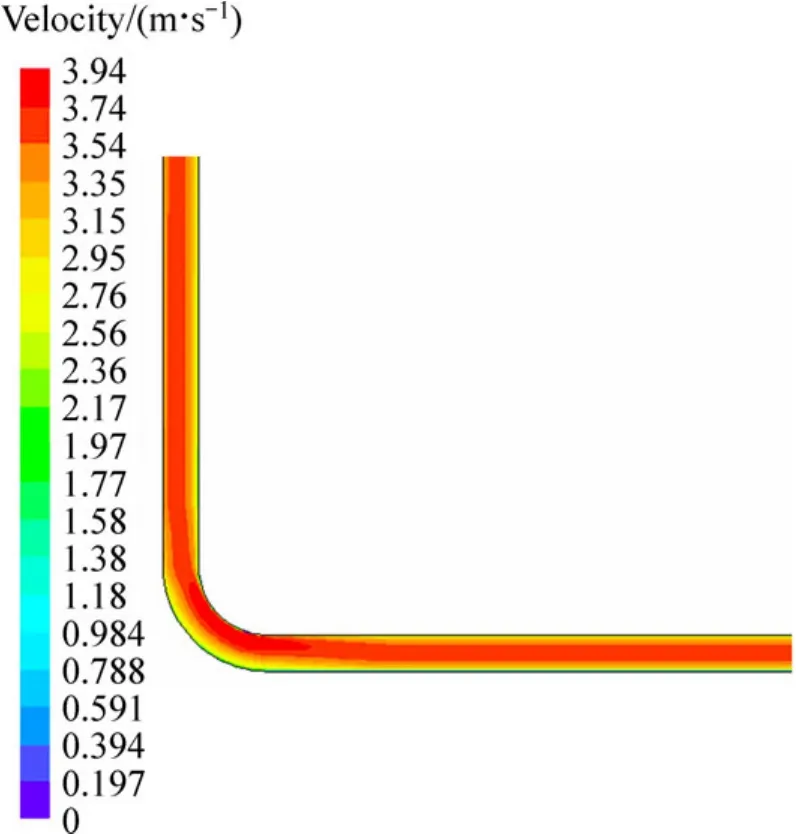
图3 弯管处料浆的速度矢量Fig.3 Velocity vector of backfilling slurry at bend of pipeline

图4 出口处料浆速度矢量Fig.4 Velocity vector of backfilling slurry at outlet of pipeline

图5 料浆在管道出口处的断面流速分布Fig.5 Velocity distribution of backfilling slurry on outlet section of pipeline
2.3 压力分析
由于在操作条件中设定弯管处的压力为0,所以进出口的压力差就是管道的阻力损失值,即压力损失为压力的最大值与最小值之差见图6)。由图6可知,管道总压最大值为1195541 Pa,最小值为-7342827 Pa,最大值与最小值相差为8538368 Pa,约为8.54 MPa。
由于该矿山采用管道自流输送,充填料浆在不通过泵加压的情况下,依靠自身重力的作用下输送到采空区。因此,由重力所产生的压力必须大于或等于管道的压力损失值才能保证料浆能顺利输送到采空区。重力所产生的压力为p=ρgh=1810×9.81×735=13050734 Pa,即 p≈13.05 MPa>8.54 MPa,所以充填料浆可以顺利输送到采空区。

图6 管道压力显示Fig.6 Display of static pressure of pipeline
从模拟分析的结果可以看出,在弯管处,料浆流速发生急剧变化,且出现最大流速,容易发生管道磨损及堵管、爆管等事故,必须采取有效措施降低管道磨损:
1)将两级阶梯管道改造成多级阶梯管道,在水平管段使用增强塑料管;
2)适当增大管道内径,采取变径管输送[18];
3)适当减小入口初速度;
4)提高钢管衬里的制造质量,保护管道,在容易磨损的弯管处使用十字管或者缓冲弯头等其他降低管道磨损的技术措施。
3 结论
1)本次研究是应用FLUENT分析超深、超长似膏体管道自流输送的一次尝试,相比于过去的研究方法,为深井充填料浆管道输送系统提供了一种全新的设计与研究思路。
2)研究了管道输送系统中料浆的流动规律。弯管处料浆流速发生急剧变化,且在此处出现流速最大值,容易发生管道磨损及堵管、爆管等事故。所以布管时,垂直管与水平管接头处应该采用高耐磨性能材质的弯管,以提高系统的安全可靠性能。
3)研究结果表明:充填料浆在工作流速为3.4 m/s,自流输送的条件下,管道最大输送速度为3.94 m/s(小于4 m/s),管道流速较理想;管道输送的压力损失为8.54 MPa,小于重力产生的压力13.05 MPa,可以满足自流输送,充填料浆管道输送系统安全可靠。
[1] NAN Shi-qing,GAO Qian,LIU Zeng-hui.Numerical simulation of fluid-solid coupling in surrounding rock and parameter optimization for filling mining[J].Procedia Engineering,2013,26:1639-1647.
[2] GONG Xue-min,ZHANG Jia-yong,GUO Li-wen.Theory and technology of backfilling in deep mines[C]//2nd.International Conference on Mechanic Automation and Control Engineering,MACE 2011-Proceedings.Piscataway,NJ,United States:IEEE Computer Society,2011:719-721.
[3] QIAO Li-wei.The application of linear motor in container-type pipeline transportation[C]//ICLEM 2010.Logistics for Sustained Economic Development Infrastructure,Information,Integration Proceedings of the 2010 International Conference of Logistics Engineering and Management.Reston,VA,United States:American Society of Civil Engineers,2010:1780-1784.
[4] HASAN S W,GHANNAM M T,ESMAIL N.Heavy crude oil viscosity reduction and rheology for pipeline transportation[J].Fuel,2010,89(5):1095-1100.
[5] 邓代强,朱永建,李 健,张友轩.基于BP神经网络的充填料浆流变参数预测分析[J].武汉理工大学学报,2012,34(7):82-87.DENG Dai-qiang,ZHU Yong-jian,LI Jian,ZHANG You-xuan.Rheology parameter forecast analysis of filling slurry based on BP neuralnetwork[J].JournalofWuhan University of Technology,2012,34(7):82-87.
[6] 瞿圆媛,邹德成,刘 宓,刘 慧,吴 淼.基于液压管式流变试验台的弯管阻力损失试验[J].煤炭科学技术,2009,37(12):69-70,87.QU Yuan-yuan,ZOU De-cheng,LIU Mi,LIU Hui,WU Miao.Experiment research on bent tube resistance loss based on hydraulic pipeline rheology test rig[J].Coal Science and Technology,2009,37(12):69-70,87.
[7] 周积果,时 炜,岑 建,刘德忠.某红土镍矿长距离矿浆管道输送工程的浓度方案研究[J].中国有色冶金,2013,42(5):7-10.ZHOU Ji-guo,SHI Wei,CEN Jian,LIU De-zhong.Study on concentration of long-distance slurry pipeline transportation project in a nickel laterite mine[J].China Nonferrous Metallurgy,2013,42(5):7-10.
[8] 张修香,乔登攀.粗骨料高浓度充填料浆的管道输送模拟及试验[J].中国有色金属学报,2015,25(1):258-266.ZHANG Xiu-xiang,QIAO Deng-pan. Simulation and experiment of pipeline transportation of high density filling slurry with coarse aggregates[J].The Chinese Journal of Nonferrous Metals,2015,25(1):258-266.
[9] ARAMAKI T L,MONTALVÃO A F,CORREA J L.Optimizing pipeline transportation using a fuzzy controller[C]//Proceedings of the Biennial International Pipeline Conference,IPC.New York,United States:American Society of Mechanical Engineers,2010:587-593.
[10] 林金贤,林 棋,娄 晨,周 军,宫 敬.气固两相流管道流动阻力特性数值模拟[J].油气储运,2014,33(1):32-41.LIN Jinxian,LIN Qi,LOU Chen,ZHOU Jun,GONG Jing.Numerical simulation of flow drag characteristics of gas-solid two-phase flow in pipeline[J].Oil& Gas Storage and Transportation,2014,33(1):32-41.
[11] 赵会军,张青松,张国忠,周诗岽,王树立.大落差顺序输送管道混油PHOENICS模拟研究[J].江苏工业学院学报,2007,19(1):41-44.ZHAO Hui-jun,ZHANG Qing-song,ZHANG Guo-zhong,ZHOU Shi-dong,WANG Shu-li.PHOENICS-based numerical study of concentration distribution of contamination on elevation difference batch pipeline[J].Journal of Jiangsu Polytechnic University,2007,19(1):41-44.
[12] 陶平凯.基于ANSYS FLOTRAN的管道输送参数优化[J].金属矿山,2012,11:43-45.TAO Ping-kai.Pipe-conveying parameters optimization based on ANSYS FLOTRAN[J].Metal Mine,2012,11:43-45.
[13] 张 刚,谷立臣,何欣荣.基于FLUENT的不定形耐火材料输送管内流动状态分析[J].耐火材料,2013,2:111-114.ZHANG Gang,GU Li-chen,HE Xin-rong.Flow state of monolithic refractories in conveying pipes based on FLUENT[J].Refractories,2013,2:111-114.
[14] 纪宏超,李耀刚,郑 镭,李文军.基于fluent的弯管流动模拟研究[J].河北联合大学学报(自然科学版),2013,35(1):73-78.JI Hong-chao,LI Yao-gang,ZHENG Lei,LI Wen-jun.The study on flow simulation based on the fluent bend pipe[J].Journal of Hebei Polytechnic University(Social Science Edition),2013,35(1):73-78.
[15] 王新民,贺 严,陈秋松.基于Fluent的分级尾砂料浆满管流输送技术[J].科技导报,2013,19(3):392-395.WANG Xin-min,HE Yan,CHEN Qiu-song.Full pipeline flowing transportation technology of classified tailings based on the fluent software[J].Science&Technology Review,2013,19(3):392-395.
[16]吴 迪,蔡嗣经,杨 威,王文潇,王 章.基于CFD的充填管道固-液两相流输送模拟及试验[J].中国有色金属学报,2012,22(7):2133-2140.WU Di,CAI Si-jing,YANG Wei,WANG Wen-xiao,WANG Zhang.Simulation and experiment of backfilling pipeline transportation of solid-liquid two-phase flow based on CFD[J].The Chinese Journal of Nonferrous Metals,2012,22(7):2133-2140.
[17]RAHMANI M,LAWRENCE G A,SEYMOUR B R.The effect of Reynolds number on mixing in Kelvin-Helmholtz billows[J].Journal of Fluid Mechanics,2014,759:612-641.
[18]高 胜,孙 文.JLG65-35节流阀油嘴的流场分布及磨蚀分析[J].化工机械,2013,40(6):805-807,832.GAO Sheng,SUN Wen.Flow field distribution and erosion analysisofJLG65-35 throttle valvenipples[J].Chemical Engineering&Machinery,2013,40(6):805-807,832.

