铝合金薄板固有变形逆解析方法的研究与开发
梁 伟 ,邓德安,MURAKAWA Hidekazu
(1. 重庆交通大学 机电与汽车工程学院,重庆 400074;2. 哈尔滨工业大学 先进焊接与连接国家重点实验室,哈尔滨 100051;3. 重庆大学 材料科学与工程学院,重庆 400044;4. Joining and Welding Research Institute, Osaka University, Osaka 567-0047)
与碳钢材料相比,铝合金的热物理性能和力学性能明显不同,主要体现在:1) 铝合金的线膨胀系数约为碳钢的2倍;2) 热传导率约为碳钢的4~5倍;3) 弹性模量约为碳钢的 1/3;4) 高温屈服强度相对较低。正是这些材料性能的不同,使得铝合金在焊接过程中更容易产生焊接变形[1]。特别是大型复杂的铝合金焊接结构件,由于影响焊接变形的因素错综复杂,如何通过结构设计优化[2]和焊接工艺优化[3]来减小和控制其焊接变形仍然是困扰焊接工作者的一大难题[4-5]。
固有应变法是预测大型复杂焊接结构件的有效方法,采用该方法预测焊接变形时,必须将分布在焊缝附近的固有变形作为已知数据代入到有限元程序中进行弹性计算[6]。如果要高精度地预测大型复杂焊接结构的焊接变形,需要建立各类典型焊接接头固有变形的数据库[7-8]。通常,对典型焊接接头而言,固有变形的成分包括纵向收缩、横向收缩、纵向弯曲、横向弯曲[9]。
目前,有两种方法可以获取固有变形:一种是实验法[10];另一种是基于热-弹-塑性有限元分析结果的积分法[11]。然而,这两种方法都有各自的局限性。当采用实验方法获取固有变形时,通常可以较精确地测量到横向收缩和横向弯曲(角变形),但由于纵向收缩和纵向弯曲的数值通常较小,常规的测量方法难以保证这两个固有变形成分的测量精度。积分法是根据热-弹-塑性有限元计算得到的残余塑性应变分布进行积分计算得到固有变形的方法, 采用该方法时必须知道材料的高温热物理和力学性能参数[12],同时,还要选取合适热源模型和定义相应的参数[13-14]。目前,各类工程结构材料的高温热物理参数和力学性能参数还不完备。另一方面,在薄板焊接接头的变形预测时,移动热源参数的定义很大程度上依靠计算者的经验[15-16]。一般而言,焊接产生的面外变形如角变形对热源模型的选取及其参数的设定都比较敏感[17],因此,采用热-弹-塑性有限元数值计算方法来获得较精确的固有变形目前尚存在一定的不确定性。
本文作者提出一种新的数值计算方法,即逆解析法来求解固有变形,并采用该方法成功地获得低碳钢典型焊接接头的固有变形[10]。前期研究表明,对低碳钢而言,纵向收缩、横向收缩、纵向弯曲和横向弯曲4个固有变形成分沿焊接线方向的分布较均匀,因此,在固有变形的逆解析时,只需计算得到各固有变形成分的平均值。但是,铝合金材料的热传导系数比低碳钢的大得多,形成准稳定的温度场(熔池形成较恒定的温度场分布)较低碳钢困难且受试件尺寸的影响明显。因此,上述4个固有变形成分在焊缝方向上的分布是否均匀,采用固有应变法预测焊接变形时,利用固有变形平均值预测的变形结果是否具有足够的精度,这些问题需要探究与证实。
本文作者基于热-弹-塑性有限元的计算结果对铝合金材料的固有变形分布特征进行了研究,在确立其固有变形分布简化模型的基础上,提出通过测量有限个代表位置上焊前与焊后的三维坐标来获得这些位置的变形量,以这些变形量为已知条件代入逆解析程序来反向求解铝合金接头4个固有变形成分的方法。
本文作者采用TIG重熔方法对铝合金薄板进行焊接并测量了其变形量,然后,采用了热-弹-塑性有限元方法计算了铝合金薄板的焊接变形,在实验验证的基础上,通过积分法获得了4个固有变形成分沿焊接线方向的分布并提出了固有变形简化模型。随后,根据简化模型,采用逆解析法计算了铝合金固有变形的各个成分。最后,通过比较实验、热-弹-塑性有限元方法及固有应变法的变形量,验证了铝合金固有变形逆解析计算方法的有效性和可行性。
1 热-弹-塑性有限元方法
金属材料在加热和冷却过程中产生的应变如式(1)所示:
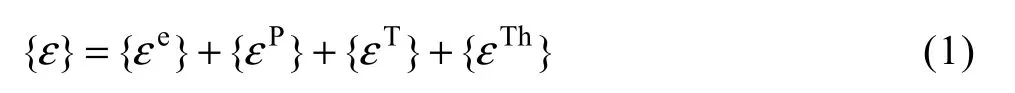
式中:{ε}是总应变;{εe}为弹性应变;{εT}是热应变;{εP}是塑性应变;{εTh}是相变应变。对焊接过程而言,达到完全冷却的状态后,热应变为 0,如果材料在焊接过程中的相变特征不明显,相变引起的变形也可忽略不计。在这种情况下,完全冷却后的残余塑性应变值即为固有应变。
将固有应变作为初始应变代入基于固有应变理论的弹性有限元模型中就可以快速求解焊接残余应力及变形。理论上而言,固有变形的精度越高,最终获得的焊接变形和残余应力的计算结果精度也就越高[7]。采用热-弹-塑性有限元法获取固有变形时,通常将焊接接头的中央断面上残余塑性应变分布或整个模型上的残余塑性应变平均值进行积分运算来得到纵向收缩、横向收缩、纵向弯曲和横向弯曲。
由于5083铝合金的高温性能参数相对比较完备,本文作者选用该牌号的铝合金为研究对象,同时基于热-弹-塑性有限元方法预测了单道 TIG重熔产生的焊接变形。
1.1 有限元模型
热-弹-塑性有限元模型如图1所示,尺寸为300 mm×200 mm×3 mm。为了方便和实验结果比较,本文作者采用全板模型来进行温度场和应力场的计算。在此计算模型中,沿焊接线方向将整个模型分为 150等份,沿板厚方向将模型等分为4等份,板宽方向分割数为45份,采用了非等宽分割;节点总数为33975,单元总数为26400。
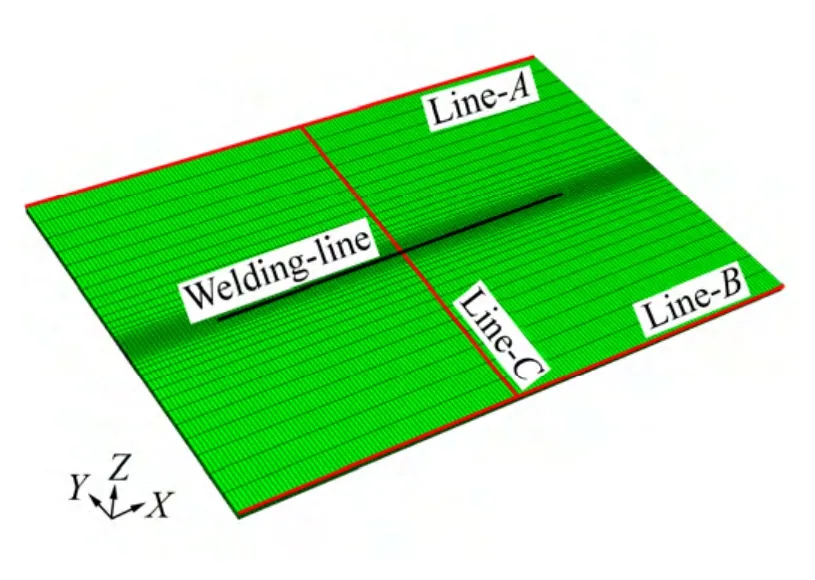
图1 热-弹-塑性有限元模型和特征线Fig. 1 Thermal-elastic-plastic FEM model and definition of several lines
焊接位置如图1中的焊接线(Welding- line)所示,焊接起始端和终止端离试件两端的距离为50 mm,焊缝长度为 200 mm。模拟时假设整个焊接过程没有外拘束,即在自由状态下进行。焊接工艺参数设定为电流200 A,电压20 V,焊接速度20 mm/s。
热-弹-塑性 FEM 分析利用的是大型商用软件ABAQUS提供的Standard求解器,采用顺序耦合法来模拟焊接变形,即焊接加热和冷却过程中形成的温度场以热载荷的形式加载到应力应变的计算模型中求解变形。本研究中采用等密度椭球体积热源来模拟焊接热输入,同时考虑了工件与周围空气的对流和辐射边界条件。温度场计算时,考虑了材料的高温热物理性能,随温度变化的热物理性能参数如图2(a)所示。
由于铝合金薄板刚性低,可以预见在焊接时可能会出现几何非线性现象,因此,在热-弹-塑性有限元中除了考虑材料非线性问题外,还考虑了几何非线性问题。铝合金高温力学性能参数如图2(b)和(c)所示。

图2 材料高温性能参数Fig. 2 Temperature dependent material properties: (a)Thermal physical properties; (b), (c) Mechanical properties
1.2 计算结果与讨论
采用上述预测方法得到的沿厚度方向的面外变形结果如图3所示。从图3可知,试板边缘Line-A(见图1)的中央位置在板厚方向的位移最大,其值为 7.42 mm,约为板厚的2.5倍。
为了验证热-弹-塑性有限元方法的精度,本研究采用实验方法实测了与有限元模型尺寸一致的 5083铝板的焊接变形。图4所示为5083铝合金试验片TIG重熔后的变形形貌。从图4中可以看到,焊接试验片的挠曲变形呈现明显的凸-凹型特征(在焊接方向为凸变形,在垂直于焊接方向为凹变。
图 5(a)比较了由有限元计算和实验得到的沿特征线Line-A和Line-B(见图1)上的挠曲变形。由图5(a) 可知,计算得到的Line-A和Line-B上的挠曲变形基本重合,充分反映出焊缝两端变形的对称性。而且,计算得到的挠曲变位最大变位为7.42 mm,距离焊板左边缘的距离为 158 mm;实验测量的最大变形量为7.60 mm,距离焊板左边缘的距离为160 mm。这些结果表明,无论是计算结果还是实测结果,在沿着焊接线方向的面外变形分布都反映出一定的非对称性,即最大变形的位置都位于焊接线中心(150 mm)偏右的位置;而且,实验反映出来的变形非对称性比计算结果更强一些。
图5(b)比较了由有限元计算和实验得到的沿中央断面,即特征线 Line-C(见图 1)上的挠曲变形。由图5(b)可知,除熔池中心外,中央断面的计算结果和实验测量结果无论在数值上还是在分布上都具有较好的吻合度。
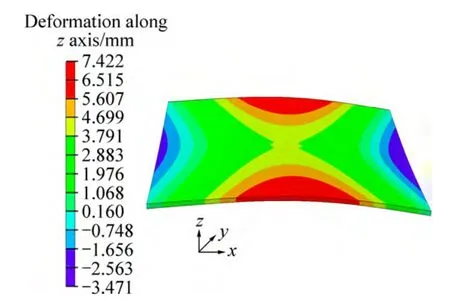
图3 厚度方向位移云图Fig. 3 Out-of-plane deformation simulated by FEM

图4 5083铝合金接头的焊接变形Fig. 4 Welding deformation of 5083Al alloy joint
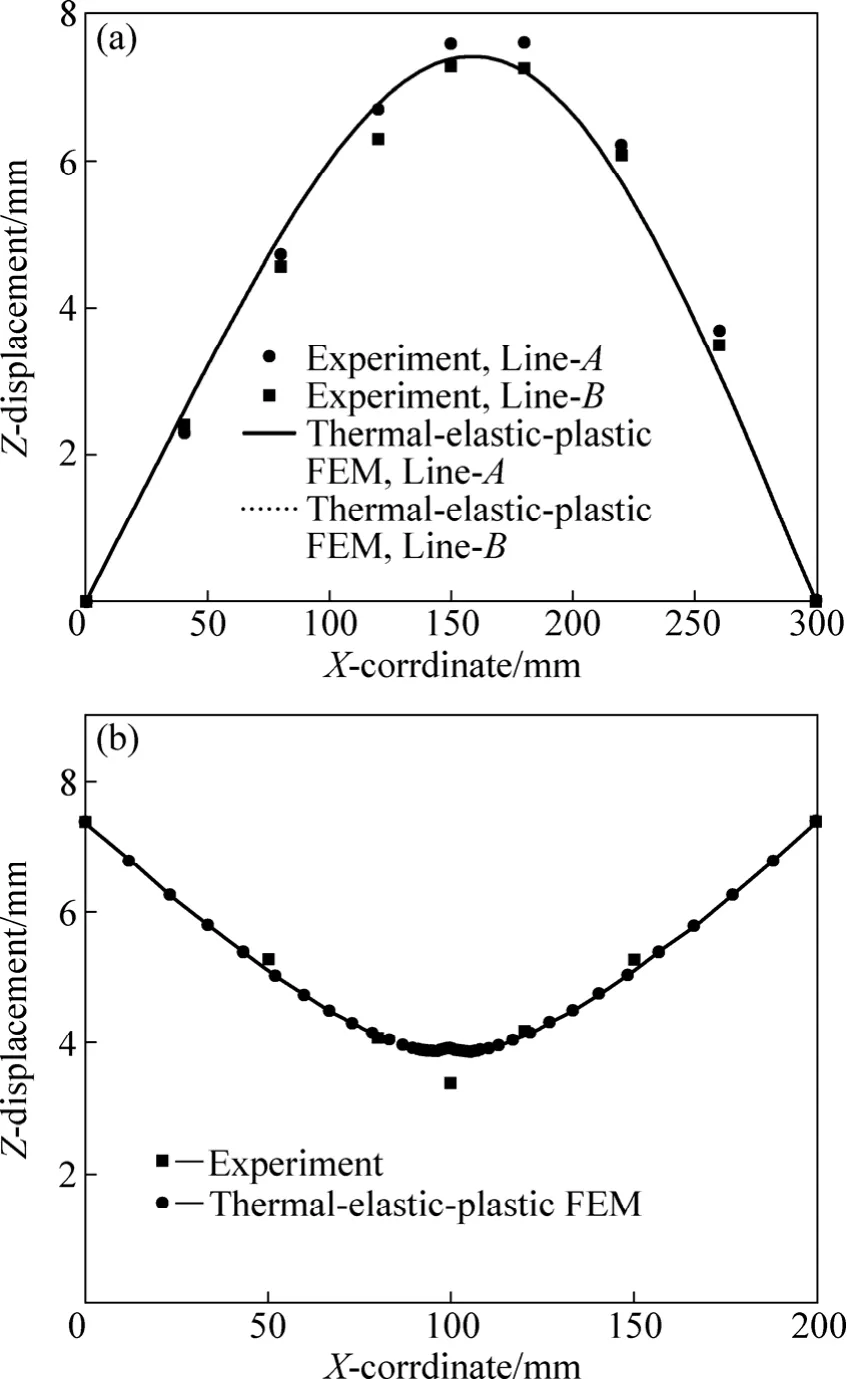
图5 特征线上的挠曲变形Fig. 5 Deflection along characteristic Lines: (a) Along Line-A and Line-B; (b) Along Line-C
2 固有变形分布特征及其简化模型的确立
2.1 铝合金固有变形分布特征
根据文献[5]提出的获得固有应变的方法,通过式(2)~(5)计算得到接头的固有变形。

将热-弹-塑性有限元计算得到的沿焊接线方向各断面的塑性应变代入到上述积分表达式,可得到各固有变形成分沿焊缝方向的分布。作为面内变形及面外变形的代表,图6(a)和(b)分别表示铝合金材料沿焊缝方向分布的纵向变形和纵向弯曲的分布。
2.2 固有变形分布简化模型的确立
固有变形的逆解析法是基于固有应变理论,通过测量少数点的三维坐标的方法反推定接头固有变形的数值计算方法。从理论上讲,如果各固有变形成分可用n个参数来表示,那么,除去6个自由度的刚体位移,焊接接头三维坐标的测量位置数 m需满足式(6)才能保证逆解析得到数值解。
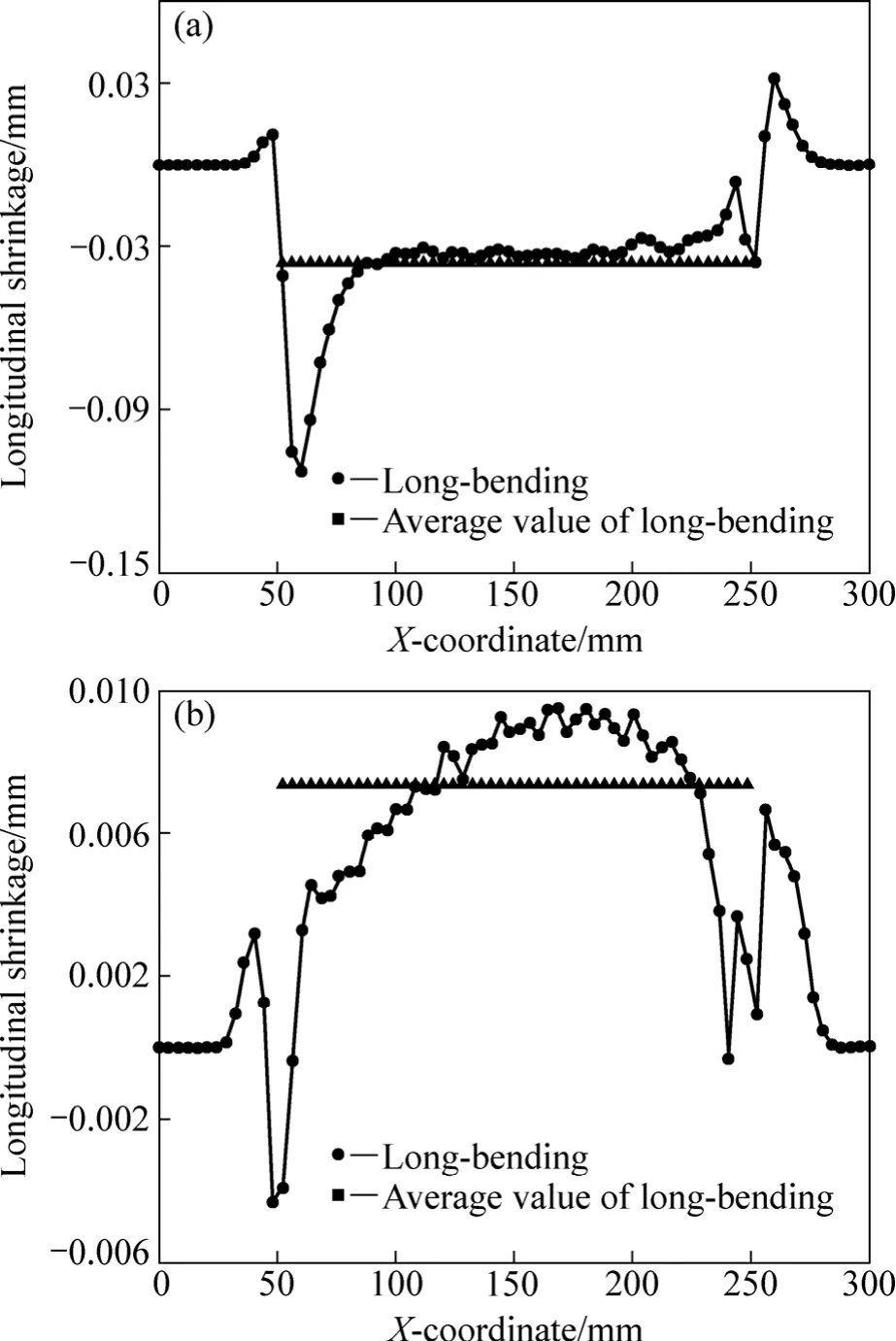
图6 固有变形沿焊缝方向的分布Fig. 6 Distribution of inherent deformation along welding Line: (a) Longitudinal shrinkage distribution; (b) Longitudinal bending deformation

从实际需求方面考虑,三维坐标测量点数不仅可以使固有变形求解工作变得方便快捷,求解得到的固有变形各成分也能更方便地带入到固有应变有限元程序中预测焊接变形。由此可见,采用逆解析方法计算固有变形最关键的问题就是确立固有变形分布的简化模型(决定n值)。
从图6中可以看到,铝合金焊接时,无论是面内变形还是面外变形,除了焊缝的起始端和终止端外,在整条焊缝上分布相对均匀,如果沿着焊缝方向的固有变形,各成分采用平均值(固有变形的积分值除以焊缝长度)代入到固有应变法的顺解析程序中也能再现热-弹-塑性变形计算的结果,那么固有变形在逆解析时,就有可能在三维坐标的测量数目更少的情况下获得较为精确的有效解。为此,本文作者将图6红线所示各固有变形的平均值作为初始应变代入到板单元的弹性有限元模型中,采用固有应变方法计算了相同焊接条件下的焊接变形。
图7所示为采用固有应变法方法得到的板厚方向的变形云图。从图7可以看出,由于固有应变法预测变形时,固有变形的各成分是以平均值的形式代入到焊缝附近的塑性变形区域,所以在特征线上的挠曲变形呈现对称特性,最大挠曲变形位于X轴中央部位。从图7中可以看到,挠曲变形分布和实验测量结果与热-弹-塑性计算得到的变形趋势吻合。
为了更详细地比较挠曲变形,这里把由固有应变法计算得到的特征线Line-A和Line-C(见图1)沿板厚方向的位移分布与由热-弹-塑性有限元计算得到的结果如图8所示。从图8中可以看到,在焊接线方向,两种计算方法都得到凸型的挠曲变形的特征,在焊接线的垂直方向都得到了凹型的变形特征,这种变形特征和实验结果吻合。从具体的挠曲变形量看,采用固有应变弹性解析法得到的最大挠曲变形量约为 7.15 mm,尽管这个值比热-弹-塑性方法得到的最大变形量7.42 mm值和实验测量的7.58 mm稍小,但整体而言它们之间有较好的吻合度。
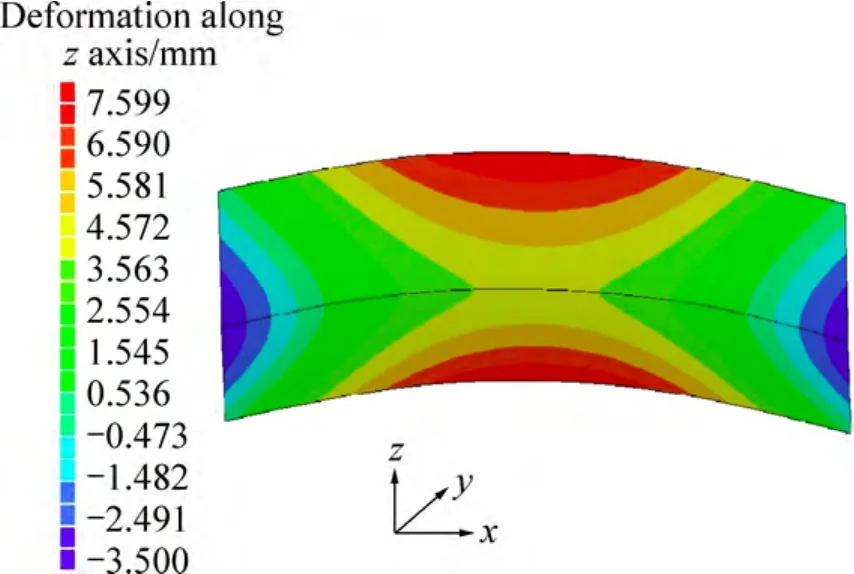
图7 采用固有应变法计算得到的面外变形Fig. 7 Out-of-plane deformation calculated by inherent strain method
3 铝合金固有变形逆解析
由图8可知,无论在焊缝方向还是在垂直于焊缝的方向上,采用固有应变的弹性有限元方法都能较好地再现热-弹-塑性有限元的结果,采用4成分的固有变形平均值可以用来预测铝合金薄板的焊接变形,而且计算精度较高。结果表明:对铝合金而言,利用固有变形平均值来代替沿焊接线方向的固有变形分布具体值是有效的。在确立了利用固有变形平均值来预测焊接变形的精度后,基于式(6)确定了如图9所示的固有变形逆解析需要的三维坐标测量点的布局。为了提高固有变形的求解精度,文中使用BRTApe×710接触式三维坐标测量系统对接触点的三维坐标进行了测量[5]。

图8 沿特征线的挠曲变形比较Fig. 8 Comparison of deflection distributions along Line A (a)and Line C (b)
逆解析分析采用了与热-弹-塑性 FEM 分析尺寸相同、拘束条件相同的板壳单元有限元模型。将焊接前后分别测得的上述 16个点的三维坐标代入到所开发的铝合金薄板焊接接头逆解析有限元程序中,则可得到固有变形值。
需要强调的是,由于铝合金变形倾向大,固有变形与最终产生的焊接变形之间的非线性关系与低碳钢相比更加明显,在逆解析时,也基于大变形理论考虑了几何非线性。固有变形的逆解析过程中固有变形与变形量之间的关系如图10所示。图10中,Fjm代表实验测量得到的变形量;Fj(ai)是采用固有变形弹性有限元方法获得的变形量;ai指固有变形的4成分。固有变形和试件的焊接变形之间的关系可以通过式(7)来表示。

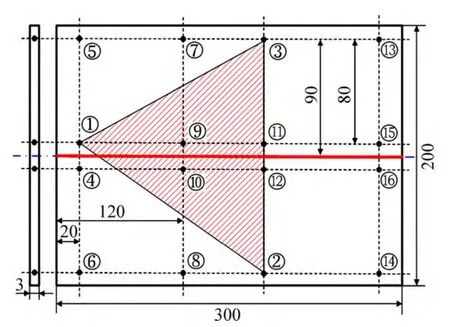
图9 三维坐标计测位置的分布Fig. 9 Arrangement of measurement points of 3D-coordinate(Unit: mm)
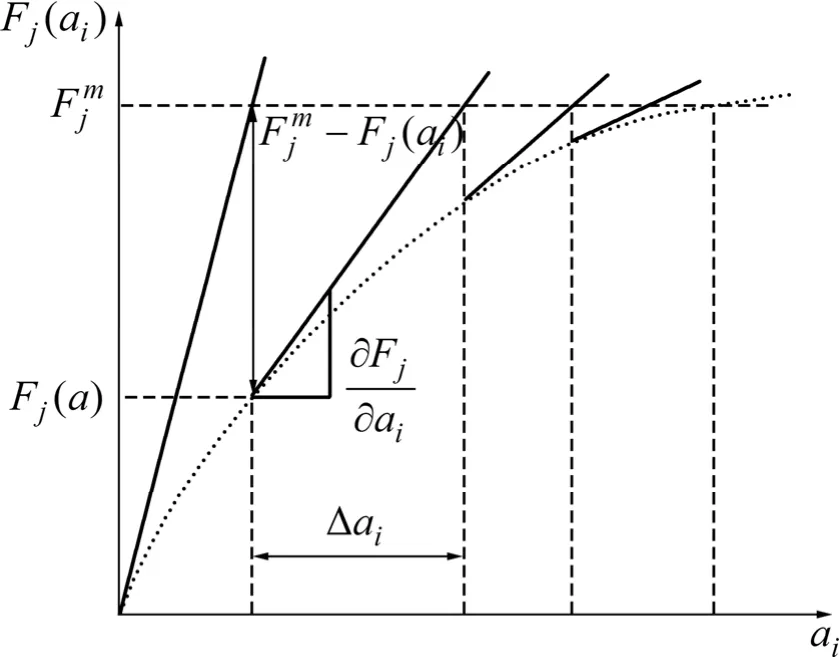
图10 采用大变形理论求解固有变形的迭代过程Fig. 10 Iterative procedure for obtaining variable ai by large deformation method
在逆解析时,固有变形ai通过以下的Tailor方程反复迭代逼近测量结果得到

式中:Δai是反复迭代过程中前一步得到的固有变形近似值。
在有限元求解时,为了得到正规矩阵,将上述式(9)的两端同乘的转置矩阵,Δai可以通过式(10)得到。
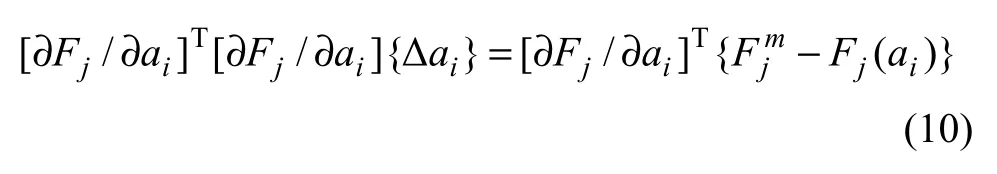
4 变形计算结果及分析
利用逆解析得到的固有变形各成分,通过固有应变顺解析方法可以得到铝合金薄板焊接变形。利用逆解析法得到的固有应变计算得到的面外变形结果如图11所示。整体上而言,图11较好地再现了热-弹-塑性FEM的结果(见图3)和实验结果(见图4)。
为了详细比较采用两种不同数值计算方法的结果,即积分法和逆解析法获得的固有变形预测的焊接变形分布和大小,图12(a)和(b)分别对焊接线Welding Line(见图 1)和中央断面上 Line-C(见图 1)的变形量作了对比。在图12(a)中,横坐标表示焊板沿焊缝方向的长度,纵坐标表示沿厚度方向上的变位值。在图12(b)中,横坐标表示板宽方向的长度,纵坐标表示中央断面上沿厚度方向上的变位值。
比较图12中不同的数值计算方法的结果可知,利用积分法或逆解析法获得的固有变形预测的挠曲变形度基本吻合,而且能较好地再现实验结果。该结果表明:采用本研究提出的固有变形逆解析方法获得的固有变形是可靠的,利用该数据能较为精确地预测铝合金薄板的焊接变形。
在本研究提出的逆解析方法中,由于直接采用焊接接头在焊接前后的有限个位置的变形量,实际上是通过每两点之间的距离变化,来反求固有变形,从方法上而言,本身具有较高的精度保障。一般来说,当各个固有应变成分沿着焊缝方向分布不是过分奇异(梯度过大) 的情况下,可以采用本研究提出的方法来获取接头的平均固有应变(等效固有应变)。
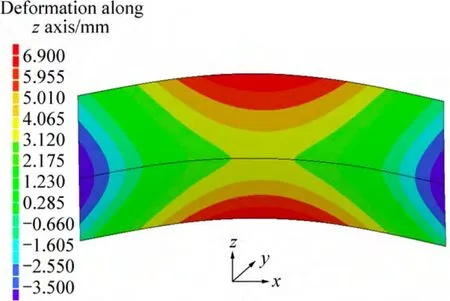
图11 厚度方向的变形云图Fig. 11 Out-of-plane deformation distribution simulated by elastic FEM

图12 沿板厚方向上焊接变形的比较Fig. 12 Comparison of deflection distributions along characteristic lines: (a) Along Line-C; (b) Along welding line
5 结论
1) 基于热-弹-塑性有限元数值计算方法预测的焊接变形较好地再现了铝合金薄板的实验测量结果。该结果表明铝合金固有变形沿焊接线分布的确立方法有效。
2) 利用铝合金固有变形各成分的平均值来预测铝合金薄板焊接变形,可以较精确地再现热-弹-塑性计算的结果。该结果表明采用逆解析方法求解铝合金固有变形各成分时,可以假设每个固有变形成分沿焊缝方向呈现均匀分布。
3) 利用固有变形逆解析方法得到的固有变形来预测铝合金薄板焊接变形,可以更精确地再现热-弹-塑性 FEM 获得的结果,该结果表明通过固有变形逆解析数值计算方法得到的固有变形正确有效。
4) 本研究提出的获取固有变形的逆解析方法可以克服实验法测量纵向收缩和横向弯曲的精度问题,同时也可以弥补热-弹-塑性有限元法的高温材料参数不充分的缺陷, 是一种获得铝合金接头固有变形的新方法。
[1] 王炎金. 铝合金车体焊接工艺[M]. 北京: 机械工业出版社,2009.WANG Yan-jin. Welding process of aluminum alloy train[M].Beijing: China Machine Press, 2009.
[2] 方洪渊. 焊接结构学[M]. 北京: 机械工业出版社, 2008.FANG Hong-yuan. Welding structures[M]. Beijing: China Machine Press, 2008.
[3] KUMAR R, SINGH K, PANDEY S, Process forces and heat input as function of process parameters in AA5083 friction stir welds[J]. Transaction Nonferrous Metals Society of China, 2012,22(2): 288-298.
[4] 周广涛, 黄海瀚, 方洪渊. 随焊超声波激振法控制铝合金薄板焊接应力及变形[J]. 中国有色金属学报, 2014, 24(4):919-925.ZHOU Guang-tao, HUANG Hai-han, FANG Hong-yuan.Controlling welding stress and distortion of aluminum alloy sheet by welding with trailing ultrasonic vibration method[J].The Chinese Journal of Nonferrous Metals, 2014, 24(4):919-925.
[5] 王炎金, 丁国华, 王俊玖. 铝合金车体制造技术在中国的发展现状和展望[J]. 焊接, 2004, 10: 5-7.WANG Yan-jin, DING Guo-hua, WANG Jun-jiu. Status and prospect of manufacture technology about aluminum alloy bodywork[J]. Welding and Joining, 2004, 10: 5-7.
[6] WANG J, YIN X, MURAKAWA H. Experimental and computational analysis of residual buckling distortion of bead-on-plate welded joint[J]. Journal of Materials Processing Technology, 2013, 213: 1447-1458.
[7] UEDA Y, MURAKAWA H, MA J. Welding deformation and residual stress prevention[M]. New York: Elsevier, 2012.
[8] 徐济进, 陈立功, 汪建华, 倪纯珍. 基于固有应变法筒体对接多道焊焊接变形的预测[J]. 焊接学报, 2007, 28(1): 77-80.XU Ji-jin, CHEN Li-gong, WANG Jian-hua, NI Chun-zhen.Prediction of distortion based on inherent strain method in multipass girth-butt welded pipes[J]. Transactions of the China Welding Institution, 2007, 28(1): 77-80.
[9] LIANG W, MURAKAWA H. An inverse analysis method to estimate inherent deformations in thin plate welded joint[J].Materials and Design, 2012, 40: 190-198.
[10] LIANG Wei. Prediction of welding distortion of large structure using inherent deformation estimated by inverse analysis[D].Osaka: Osaka University, 2005.
[11] LIANG W, MURAKAWA H. Predicting welding distortion in a panel structure with longitudinal stiffeners using inherent deformations obtained by inverse analysis method[J]. The Scientific World Journal, 2014, 8: 1-8.
[12] 叶延洪, 何 静, 蔡建鹏, 孙加民, 邓德安. 6061-T651 铝合金薄板接头的焊接变形[J]. 中国有色金属学报, 2014, 24(10):2435-2442.YE Yan-hong, HE Jing, CAI Jian-peng, SUN Jia-min, DENG De-an. Welding deformations of 6061-T651 Al alloy thin-plate joints[J]. The Chinese Journal of Nonferrous Metals, 2014,24(10): 2435-2442.
[13] 王能庆, 童彦刚, 邓德安. 热源形状参数对薄板焊接残余应力和变形的影响[J]. 焊接学报, 2012, 33(12): 97-100.WANG Neng-qing, TONG Yan-gang, DENG De-an. Effects of welding heatsource parameters on residual stress and distortion in thin plate joint[J]. Transactions of the China Welding Institution, 2012, 33(12): 97-100.
[14] 武传松. 焊接热过程数值分析[M]. 哈尔滨: 哈尔滨工业出版社, 1990.WU Chuan-song. Numerical analysis of welding thermal process[M]. Harbin: Harbin Institute of Technology Press, 1990.
[15] 邓德安, KIYOSHIMA S. 用可变长度热源模拟奥氏体不锈钢多层焊对接接头的焊接残余应力[J]. 金属学报, 2010, 46(2):195-200.DENG De-an, KIYOSHIMA S. Numerical simulation of welding residual stresses in a multi-pass butt-welded joint of austenitic stainless steel using variable length heat source[J].Acta Metallurgica Sinica, 2010, 46(2): 195-200.
[16] 曹淑芬, 陈铁平, 易 杰, 郭鹏程, 李落星. 铝合金双脉冲MIG焊过程的温度及应力变形模拟[J]. 中国有色金属学报,2014, 24(7): 1686-1692.CA Shu-fen, CHEN Tie-ping, YI Jie, GUO Peng-heng, LI Luo-xing. Simulation of temperature, stress and deformation during double pulsed MIG welding of aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(7): 1686-1692.
[17] DENG D A, LIANG W, MURAKAWA H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements[J]. Journal of Materials Processing Technology,2007, 183: 219-225.

