加权投资者关系网络的股市传闻扩散演化模型

卞曰瑭，许 露

(1.南京师范大学 商学院，江苏 南京 210023;2.南京铁道职业技术学院，江苏 南京 210031)

股市是现代金融体系的重要组成部分，也是维系整个经济系统正常运转不可或缺的金融中介组织，是衡量资本运行效率、行业运转前景和经济发展态势等的重要手段。系统分析股票市场中传闻扩散机理及其演化机制，对于有效研判股票市场乃至金融系统的动态演变具有重要作用［1-2］。基本上，股市传闻被学术界界定为“一种未经证实就充斥于股票市场中并得以流传的信息”，其主要源于市场间流传的小道消息、股评分析和新闻媒体报道等多种渠道，涉及上市公司的投融资决策、并购重组动态、经营财务状况以及产业、财政和货币政策等［3］。

目前关于股市传闻扩散问题的研究主要集中在股市传闻扩散机理分析和股市传闻扩散模型构建两个层面。其一，针对股市传闻扩散机理，学者们主要从传闻扩散主体特征、传闻扩散渠道、传闻扩散影响因素以及传闻扩散的波及效应等视角进行分析。如:Schindler 调查发现决定大多数投资者是否继续传递市场传闻的因素是传闻传递人以及市场价格变动情况［4］。Einwiller 和Kamins 指出对传闻目标认同程度是影响其扩散的一个重要因素［5］。此外，有部分学者如Roshani 等［6］围绕传闻对交易行为的影响及差异进行了研究。其二，现有关于股市传闻或谣言等信息扩散模型大致可以分为宏观层面的模型构建和微观层面的模型构建:(1)经典宏观层面的模型Daley-Kendal 模型由Daley 和Kendal［7］最早提出，随后其他学者不断对其进行了改进。这些模型被广泛应用于对传闻扩散的定量研究中［8］。(2)微观层面模型的建立主要采用渗流模型［9］、元胞自动机［10］、传染病模型［11］等复杂系统理论和方法进行研究。如Gai 和Kapadia 基于传染病模型研究金融网络中的谣言传染性来评估金融系统的脆弱性问题［12］。Shive 基于传染病模型分析了诸如传闻、文化等社会性因素对交易者行为和资产价格的影响［13］。Isham 等构建了不同扩散机制和网络拓扑结构下的谣言扩散模型［14］。Zhang 等针对谣言扩散过程的多重演变性，构建了不同网络结构特征下的谣言扩散模型［15］。

总体而言，国内外学者针对金融市场中的传闻或谣言等信息扩散和演化研究已取得较为丰硕的成果;近年来，更多文献专注于采用复杂系统理论和方法来分析此类问题。然而，现有研究大多考虑均质网络结构下的股市传闻扩散，且对于市场参与者对待传闻的态度和行为上，没有考虑过参与者的记忆性行为机制，而这与现实情况不符，现实中的市场参与者除忘记或疏忽而自发地停止传播传闻外，也会因为记忆而重新想起该传闻并继续进行传播扩散。因此，针对投资者间的内在耦合关联性，基于传染病SIR 模型，增加股市传闻扩散休眠者这一类市场参与主体，构建了加权投资者关系网络结构下的股市传闻扩散演化模型，并通过数理解析与模拟仿真方法相结合，系统分析股市传闻传播的规律性特征，以期为监管部门制定政策提供理论支撑。

一、模型构建

自然界和社会中的几乎所有复杂系统都可以抽象为网络模型［16］。因而，股市传闻扩散演化系统同样可通过网络结构来描述，其中:网络节点代表股市投资者，节点间的连边代表投资者间的某种关联，如:社会关系、交易关联等。基于此，假定由N 个节点构成的投资者网络系统G=(N，V)，令N={1，2，...，i，...，n}，其中(i，j)∈V 表示节点i 和j 之间存在连接，且假定网络中不存在孤立节点;设定ki代表节点i 的度，表示节点i 具有ki个邻居;可用表示网络节点度分布，反映度为k 的个体在群体中的比例，其中0 ＜k ＜N［17］。

(一)股市传闻扩散的演化机理分析

在股票市场，知情投资者或市场参与者可借助于相互间的各类关系渠道，将市场传闻在投资者中扩散开来，一定程度上影响其他投资者的投资策略，通过作用于市场来获取超额收益。现实中，投资者因为在专业知识、投资技能、风险偏好等方面的差异性，导致各自对股市传闻的认知、判断及处理的效应和效果不同。部分投资者因对市场中的信息有一定的辨识能力，不会轻易相信市场中流传的所有信息;部分投资者因投资兴趣偏好或生活、工作事务等繁重而疏忽或遗忘传播消息;也有部分投资者先前遗忘市场传闻，而后又重新关注并继续进行传播扩散。

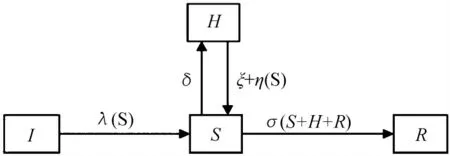
图1 基于SIHR 模型的股市传闻扩散状态转变示意

基于此，本文将股市投资者分为以下4 类:股市传闻扩散者S、股市传闻未知者I、股市传闻扩散休眠者H 和股市传闻扩散免疫者R，由此构建基于投资者关系网络的SIHR 股市传闻扩散模型，其基本演变规则如下:(1)若传闻扩散者S 与传闻未知者I 接触，传闻未知者I 以概率λ(称为扩散率)成为扩散者S;(2)传闻扩散者S 以速率δ(称为遗忘率)自发停止传闻扩散成为传闻扩散休眠者H。同时，传闻扩散休眠者H 又以速率ξ(称为自发记忆率)自发地成为传闻扩散者S。此外，当传闻扩散休眠者H 与传闻扩散者S 接触，前者以概率η(称为唤醒记忆率)成为传闻扩散者;(3)当传闻扩散者S 与其他传闻扩散者、传闻扩散休眠者以及传闻免疫者接触，该传闻扩散者以概率σ 变为传闻扩散免疫者R。

由此，股市传闻扩散SIHR 模型中投资者行为状态演变示意如图1 所示。

(二)股市传闻扩散的演化模型构建

基于上述分析，设任意时刻t，传闻扩散网络中度为k 的扩散节点、传闻未知节点、休眠节点和免疫节点的密度分别记为:Sk(t)、Ik(t)、Hk(t)和Rk(t)，且满足规范化条件Ik(t)+Sk(t)+Hk(t)+Rk(t)=1。根据连续相变的平均场理论，SIHR 股市传闻扩散模型中的网络节点比重随时间演变过程如下所示:

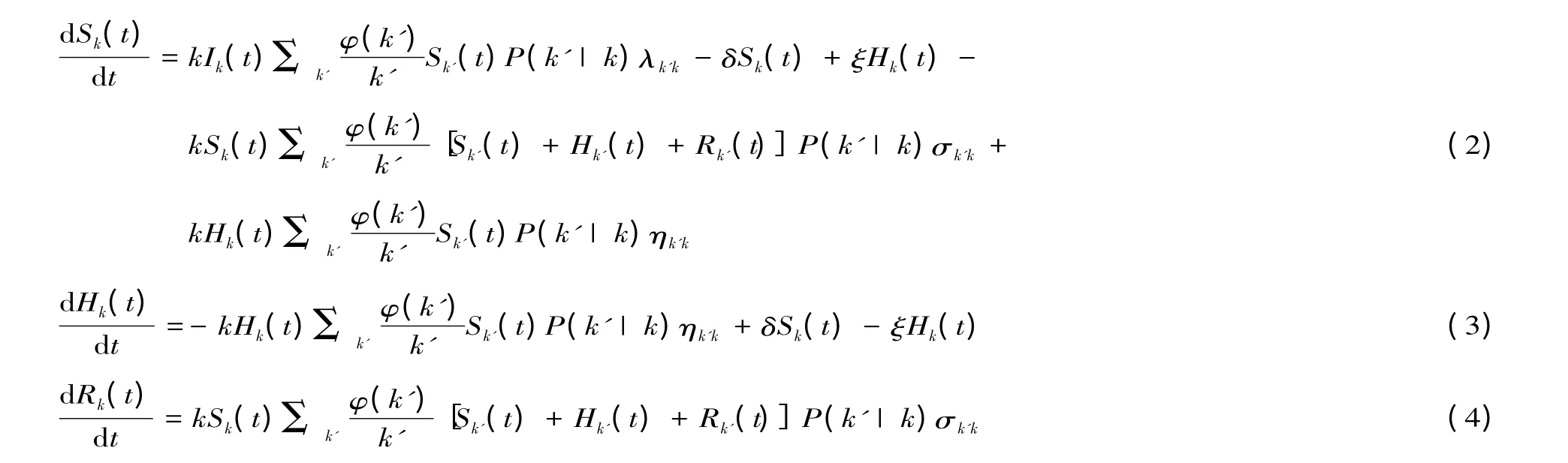
针对现实股市系统中各主体关于传闻扩散率的异同，文中分别考虑了节点权重和节点连边权重的差异性，由此构建基于加权网络的股市传闻扩散SIHR 模型。按照Barrat 等［18］提出的边权和点权的计算方法，将网络任意连边的边权界定为相应节点度k 和k'的函数，记为:wkk'=w0(kk')β;将与度为k 的节点相连的所有边的权重相加，以获得该节点的点强度，记为:其中，参数w0取正值;β 是度相关的连接强度指数，其值依赖于网络的类型。基于此，对于度为k 网络的节点，假设其总的扩散率、免疫率和唤醒率都是常数，记为λk，σk和ηk，则经度为k 和k'的节点连边扩散股市传闻的扩散率λkk'，由该边权重占度为k 节点强度的比重进行重新分配，可定义为:

即，Gk中连边权重wkk'所占比重越大，股市传闻通过该边进行扩散的概率就越高。类似地，可定义免疫率σkk'和唤醒率ηkk'分别为σkk'=σkwkk'/Gk和ηkk'=ηkwkk'/Gk。

考虑到股市投资者关系网络的度无关性［16］，则上述条件概率满足P(k'|k)=k'p(k')/〈k〉。因此，可得Gk=w0〈k1+β〉k1+β/〈k〉，从而λkk'、σkk'和ηkk'可进一步化简为:

由此，当β ＞0(β ＜0)时，市场传闻倾向于向度更大(更小)的节点传播扩散。

此外，基于上述分析，定义模型中度为k 的节点的非线性传染力函数为:

其中，0 ≤α ＜1、A ＞0。即设定在每个时间步内，扩散者可与其Akα/(A+kα)个邻居接触。不难发现，当k 相对较小时，φ(k)呈现为递增，随后逐渐饱和并无限近于常数A，这也较为合乎常理。

综上所述，把式(6)和式(7)带入到方程式(1)-(4)，可得基于平均场方程的加权网络中具有非线性传染力的SIHR 股市传闻扩散演化模型:

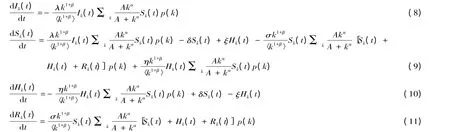
二、基于平均场方程的股市传闻扩散动力学解析

当网络规模N 足够大，且各节点同质混合分布，因投资者关系网络中各节点属性不受网络结构的影响，上述构建的股市传闻扩散演化模型无法直接获得有效解析解，为此文中通过基于平均场方程对股市传闻扩散过程演化的稳定性和阈值特征进行数理分析。

(一)股市传闻扩散状态的稳定性分析

股市传闻扩散的演化过程，可简单描述为初始传闻扩散人群规模不断增加，而后不断减少并在传闻趋于消失时，传闻扩散人群递减为零，最终在市场中只剩下传闻未知者和传闻免疫者。假设股市传闻扩散人群的最终规模为:R=R(∞)，表示传闻扩散程度。由此，通过对式(8)积分可得:

式中，Ik(0)表示度为k 的股市传闻未知节点的初始相对密度;φ(t)是辅助函数，可将其定义为:

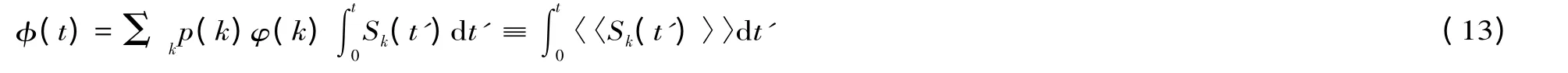
为简便，将式(13)简化描述为:

与此同时，定义另一个辅助函数ψ(t)如下:

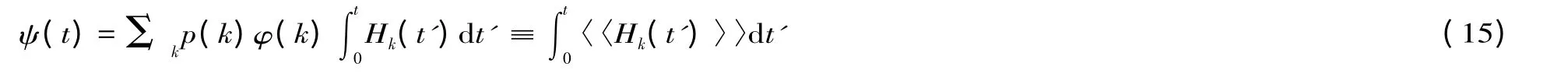
假设传闻未知节点的初始分布均匀，即Ik(t)=Ik(0)。则在式(9)两边同乘p(k)φ(k)并对k 求和，再对其在定义域［0，t］积分，易得:

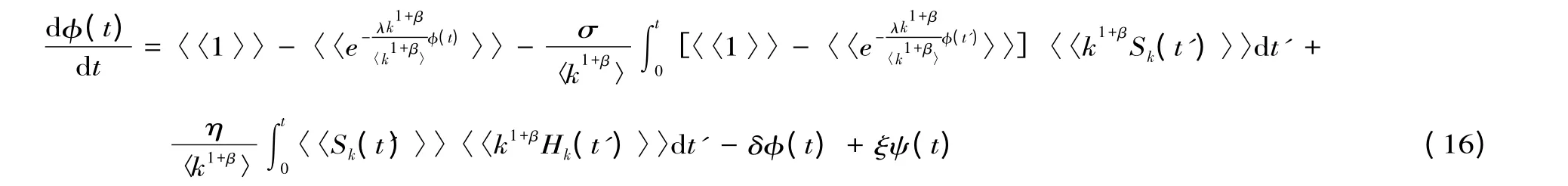
为不失一般性，设I(0)≈1。当t →∞时，股市传闻扩散趋于稳态。此时dφ(t)/dt=0，dψ(t)/dt=0。则由式(16)可得:

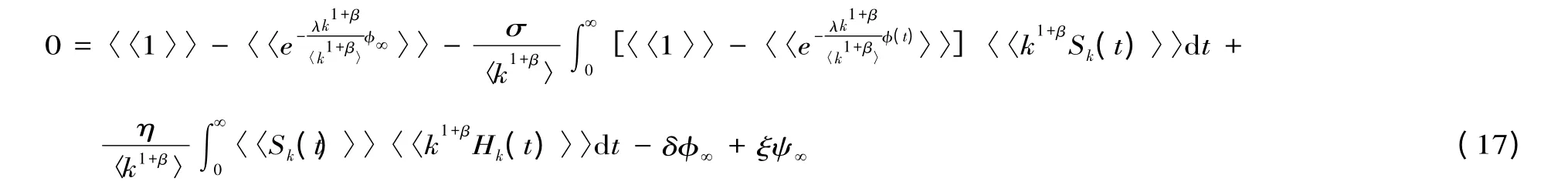
若σ=η=0，可对式(17)进行求解并可得到唯一的解φ∞=0。若σ ≠0 且η ≠0，对式(17)求解到σ 和η 的一阶项。为此，只需求得含σ 和η 零阶项的Sk(t)即可。将式(9)和(10)相加得:

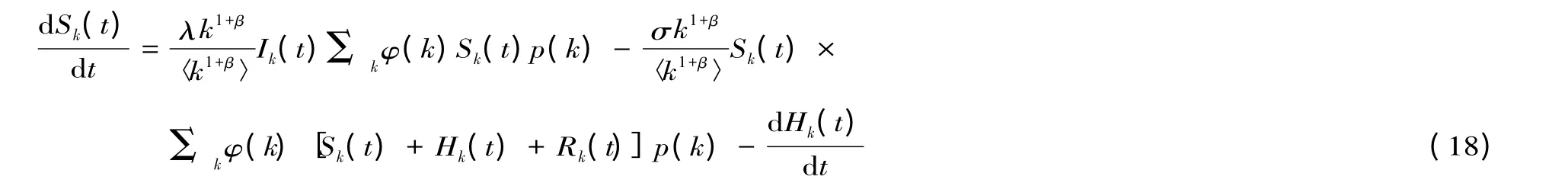
对上式在定义域［0，t］内积分，并计算到σ 的零阶项，可得:

同时，运用常微分方程对式(10)进行求解，可得只含η 零阶项的Hk(t)表达式:

基于此，将式(20)带入式(19)进行常微分方程求解，便可求得只含σ 和η 零阶项的Sk(t)表达式:

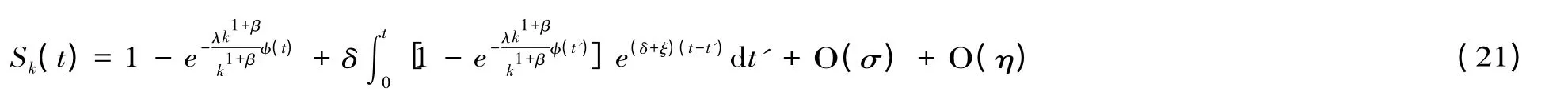
在接近阈值处，φ(t)和φ∞取值都很小，则可令φ(t)=φ∞f(t)，其中f(t)是一个有限函数。则只保留φ∞的一阶项，式(21)可近似为:

则由式(19)可得:

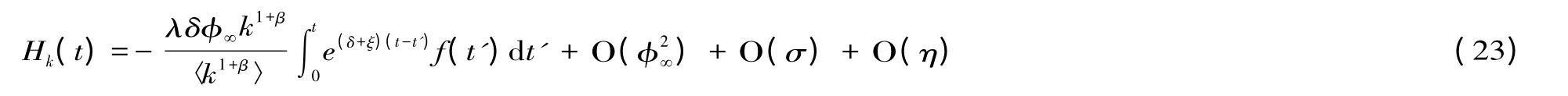
将式(22)和(23)带入式(17)，并利用泰勒展式将指数函数展开到φ∞的对应阶数，得到:

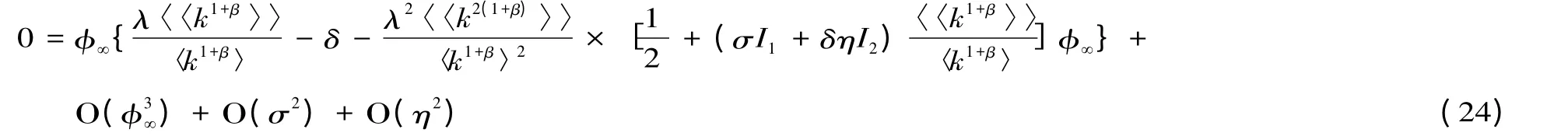
其中，I1和I2都表示正的有限定积分。因，可忽略ψ∞项，即得上述方程的非零解:

与此同时，要使得φ∞＞0，则必须满足条件:

可见，近似计算到σ 和η 的一阶项所求得的阈值不依赖于免疫率和唤醒率。尤其，当δ=1，则股市传闻扩散阈值为:。结合等式，式(25)可简化为:

由于Rk(∞)=1－Ik(∞)，则在稳态时，股市传闻扩散的最终规模为:

可见，对上述方程的求解依赖于度分布p(k)的选取。

(二)股市传闻扩散状态的阈值分析

在此基础上，进一步分析非线性传染力的加权投资者关系网络传闻扩散阈值，假定网络度分布满足:p(k)∝k－2－γ，0 ＜γ ≤1。对于有限规模的无标度网络，引入最大连接度kc，其大小取决于节点总数N 和最小连边数m，可表示为:。

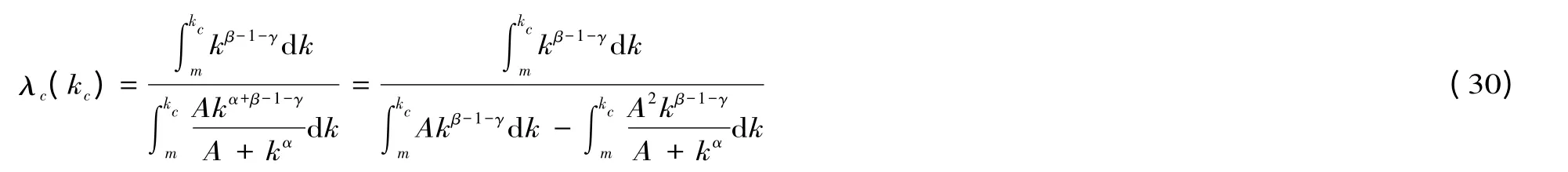
综上所述，构建的股市传闻扩散模型在有限规模加权投资者网络中始终存在正的传闻扩散阈值λc(kc)，且该阈值随着网络规模的增大而逐渐增大。

三、模拟仿真分析

针对上节中运用平均场方法对有限规模加权网络中股市传闻扩散演化的稳定性特征和阈值特征进行的数值解析，下面运用模拟仿真的方法进一步验证和诠释。设定模拟仿真实验参数如下:选取股市加权投资者关系网络［17］，投资者规模N=1 000，免疫率、唤醒率、传染指数等参数在不同实验中具体选择，演化时间段为100，做100 次循环求平均，每次实验都随机选择具有不同度的初始传闻扩散节点。

(一)免疫率、唤醒率和网络结构对股市传闻扩散的影响

图2 和图3 分别描述了不同免疫率和唤醒记忆率以及不同网络规模下，股市传闻扩散规模演变与扩散率之间的关联关系。其中，图2 中的参数取值A=100、α=β=0.5、δ=ξ=0.5、N=1 000;图3 中的参数取值A=100、α=β=0.5、δ=ξ=0.5、σ=0.6。

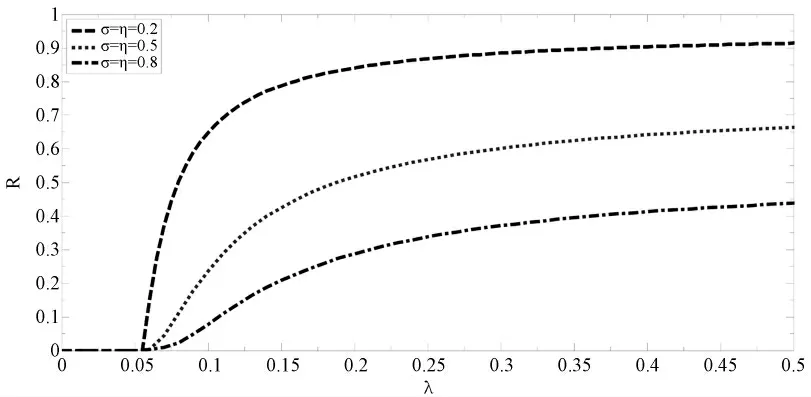
图2 σ 和η 对股市传闻扩散的影响

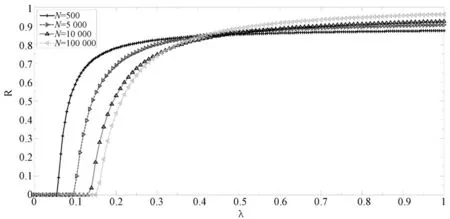
图3 网络规模N 对股市传闻扩散的影响

由图2，股市传闻扩散规模R 始终存在一个临界值λc(kc)，且不依赖于参数σ 和η。当扩散率λ 小于此临界值时，股市传闻基本难以大规模扩散。由图3，任意规模投资者网络上的股市传闻扩散阈值必然存在，且阈值λc(kc)随着网络规模N 的增大而增加，这与上述的理论解析结论基本吻合;而且，网络规模越大，股市传闻扩散阈值也越大;但当趋于稳态时，传闻的最终扩散规模也越大，这一现象在现实股市中不难理解。

(二)传染力指数和连接强度指数对股市传闻扩散的影响

图4 描述了网络节点间的连接强度指数β 对股市传闻扩散过程的影响。图中(a)、(b)、(c)和(d)4 幅图分别描述了传闻未知者、扩散者、休眠者和免疫者的扩散密度随时间的演变情况;且图中的曲线分别对应连接强度指数β 的不同取值;其中，此时取值A= 100、α= 1.0、λ= 0.8、σ= 0.6、δ= ξ= 0.5、η= 0.4。

由图4(a)，β 越大，股市传闻扩散终止时的传闻未知者的比例却越小;由图4(b)，β 越大，股市传闻扩散节点比重的峰值越高，即股市传闻越强烈则影响越广，传闻最终消失的时间就越晚;由图4(c)，指数β 对传闻扩散休眠者的影响与对传闻扩散者相似，考虑到这两类投资主体的关联性，这样的结果也符合现实特征;由图4(d)，β 越大，传闻扩散过程终止时的传闻免疫者比例越大，这与图4(a)中的结果正好相反。总体来看，当股市传闻扩散达到稳态时，市场中仅剩传闻未知者和传闻免疫者两类人群。

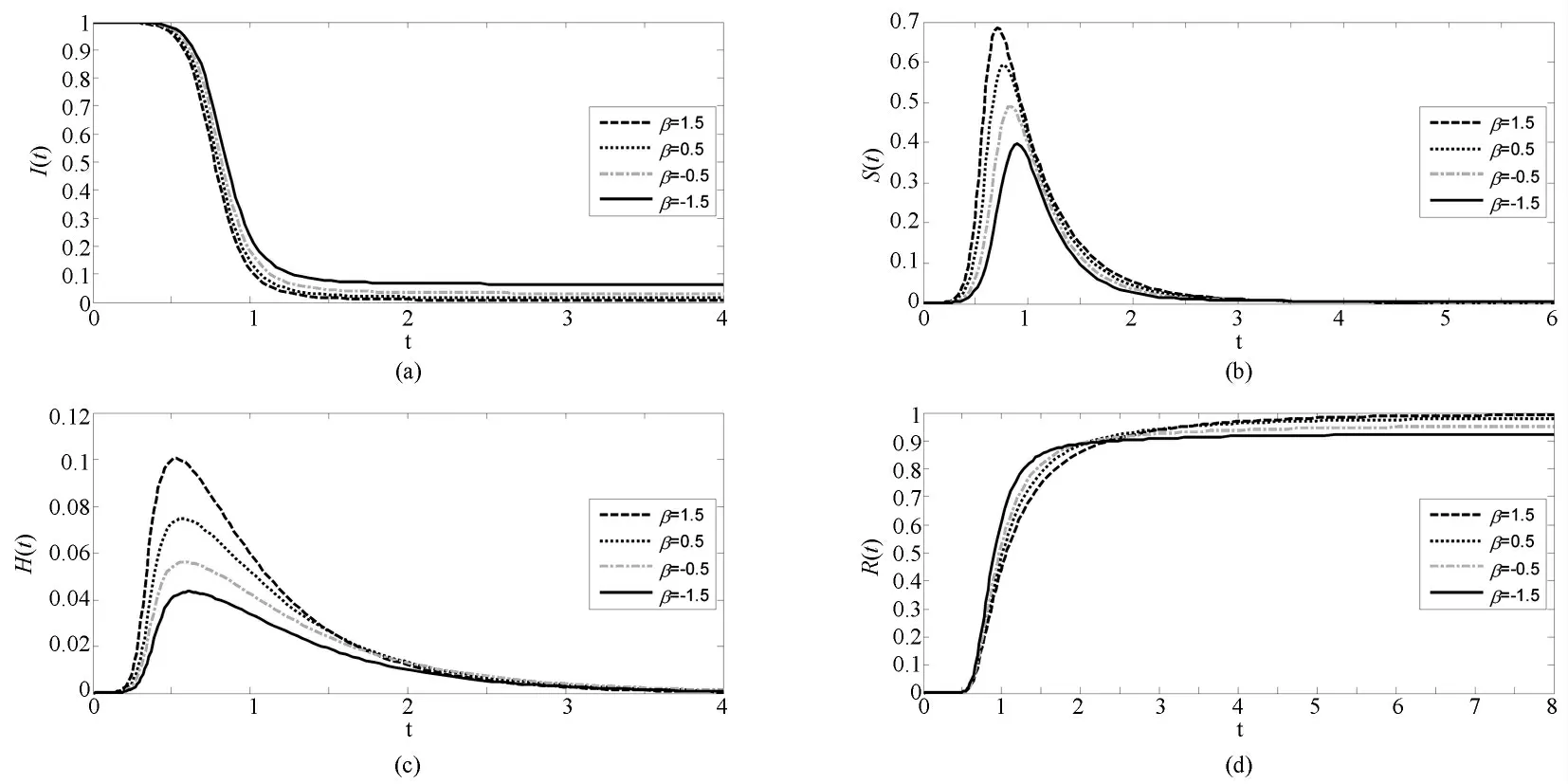
图4 连接强度β 对股市传闻扩散规模的影响

此外，由图4(d)可见，连接强度β 越小，传闻免疫者规模稳态出现越早，这与图4(b)中的结论相吻合。正如前文所述，当β ＞0(或β ＜0)时，股市传闻倾向于向节点度偏大(或偏小)的节点扩散和传播，且随着β值的增大，该趋势愈发明显。因此，基于前面分析的股市传闻扩散规则，连接强度指数越大，网络中传闻未感染的Hub 节点(度值大者)就越可能转变为传闻扩散者，这使更多的传闻未知者能接触股市传闻，从而导致稳态时的传闻未知者群体比例减小。

此外，当自发记忆率相同时，连接强度指数β 越大，度值大的传闻扩散者变为免疫者的可能性更大，从而传闻休眠者接触扩散者的概率则更小，最终使得唤醒记忆率越小。因此，连接强度指数β 越大，传闻休眠者变成扩散者的总转变概率则越小，由此延缓了传闻扩散者最终的消除时间，这也归咎于传闻休眠者必然因记忆机制从而转变为传闻扩散者。

(三)扩散率对股市传闻扩散的影响

图5 描述了不同传染力指数α 和连接强度指数β 水平下，扩散率指标对股市传闻扩散规模R 的影响。此时，取值A=100，σ=0.6，δ=ξ=0.5，η=0.4。

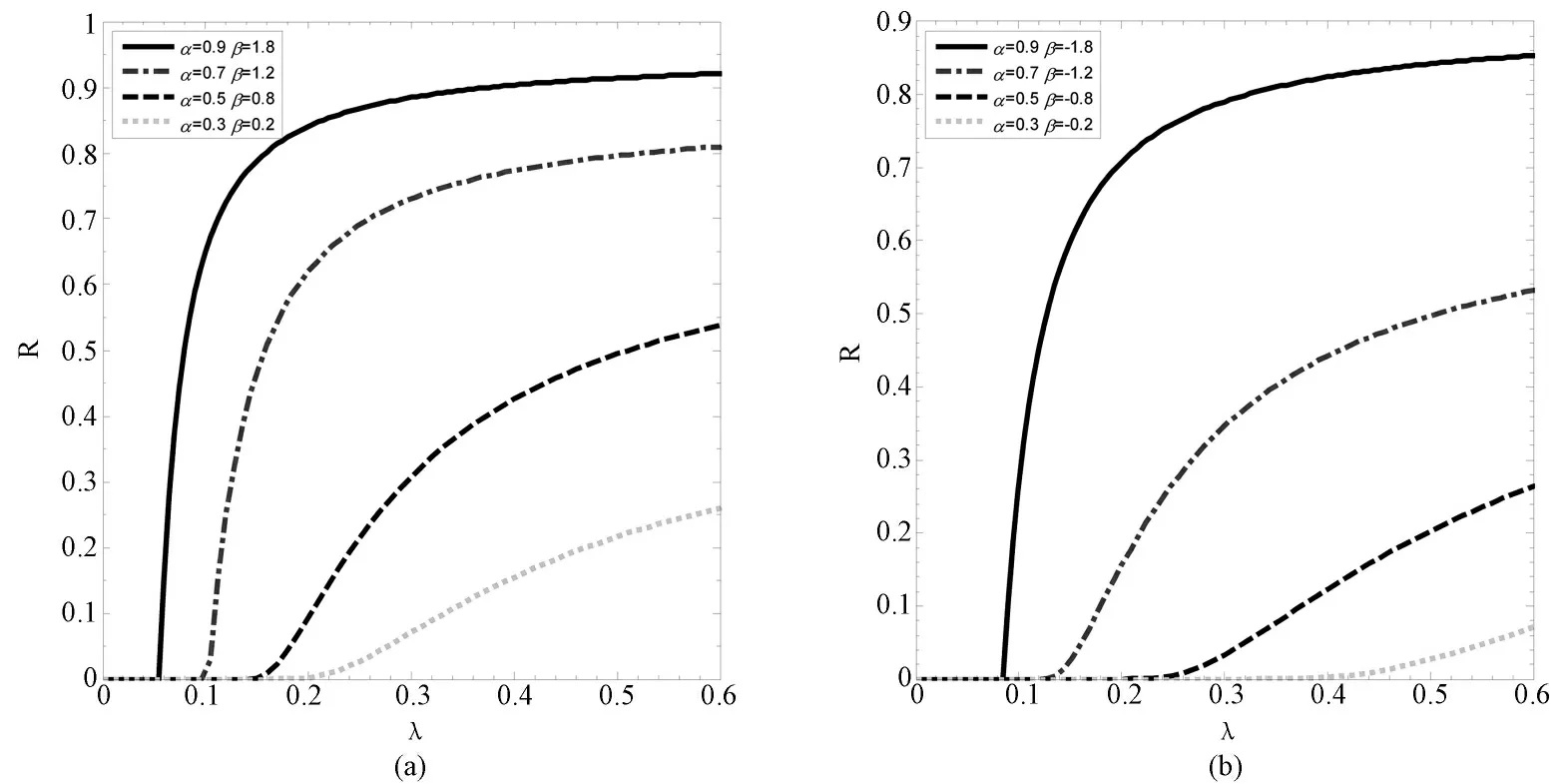
图5 不同参数下的股市传闻扩散规模与扩散率间的内在关系

由图5(a)和图5(b)，股市传闻扩散阈值始终存在，且α 越大，R 增长越快。当α 和β 共存时，指数α 对股市传闻最终扩散规模起主要作用。通过调节传染力指数α 来影响投资者的接触率，以此分析该条件下股市传闻扩散规模状态，实验结果显示，随着α 减少引起的接触数降低，股市传闻扩散阈值不断增加;而通过改变连接强度指数β 来调节投资者接触过程中的扩散率时，β 值越大越能更快地引致股市传闻扩散速度。由此可见，在基于加权网络SIHR 模型的股市传闻扩散演化过程中，对投资者之间接触程度的控制，比调节传闻在投资者接触中扩散率的效果更加显著。

四、研究结论

针对投资者间的内在耦合关系以及各主体对股市传闻信息认知、判断和处置的异质性，考虑投资者对股市传闻传播中普遍存在的遗忘性和记忆性行为特征，构建了加权投资者关系网络下的股市传闻扩散SIHR演化模型。通过数理解析和模拟仿真，研究发现:(1)股市传闻扩散演化状态的稳定性和传播阈值，受股市网络结构、传染力指数和连接强度指数影响。(2)基于加权投资者网络SIHR 演化模型的股市传闻扩散阈值必然存在;阈值与免疫机制和唤醒记忆机制无关，随着网络规模的增大而增加。(3)连接强度指数通过加权扩散率对市场传闻扩散规模的稳定状态影响显著。(4)相比于连接强度指数，传染力指数通过调节个体间相互接触的概率对股市传闻传播产生的影响居主导地位，这也表明对投资者之间接触程度的控制，比调节传闻在投资者接触中扩散率的效果更加显著。

［1］赵静梅，何欣，吴风云.中国股市谣言研究:传谣、辟谣及其对股价的冲击［J］.管理世界，2010(11):38-51.

［2］钟阳.国际金融中心的发展:资本流动与惯性效应的作用［J］.重庆大学学报:社会科学版，2014(1):31-36.

［3］BORDIA P，DIFONZO N，HAINES R，et al.Rumors denials as persuasive messages:Effects of personal relevance，source，and message characteristics［J］.Journal of Applied Social Psychology，2005，35(6):1301-1331.

［4］SCHINDLER M.Rumors in financial markets［M］.New York:John Wiley＆Sons，2007:18-20.

［5］EINWILLER S A，KAMINS M A.Rumor has it:The moderating effect of identification on rumor impact and the effectiveness of rumor refutation［J］.Journal of Applied Social Psychology，2008，38(9):2248-2272.

［6］ROSHANI F，NAIMI Y.Effects of degree-biased transmission rate and nonlinear infectivity on rumor spreading in complex social networks［J］.Physical Review E，2012，85(3):036109.

［7］DALEY D J，KENDALL D G.Stochastic rumours［J］.IMA Journal of Applied Mathematics，1965，1(1):42-55.

［8］NOYMER A.The transmission and persistence of“urban legends”:Sociological applications of age-structured epidemic models［J］.The Journal of Mathematical Sociology，2001，25(3):299-323.

［9］GOLDENBERG J，LIBAI B，SOLOMON S，et al.Marketing percolation［J］.Physica A，2000，284(1/2/3/4):335-347.

［10］GOLDENBERG J，EFRONI S.Using cellular automata modeling of the emergence of innovation［J］.Technological Forecasting and Social Change，2001，68(3):293-308.

［11］HAUSKEN K，PLUMPER T.Containing contagious financial crises:The political economy of joint intervention into the Asian crisis［J］.Public Choice，2002，111(3):209-236.

［12］GAI P，KAPADIA S.Contagion in financial networks［R］.London:Bank of England，2007.

［13］SHIVE S.An epidemic model of investor behavior［J］.Journal of Financial and Quantitative Analysis，2010，45(1):169-198.

［14］ISHAM V，HARDEN S，NEKOVEE M.Stochastic epidemics and rumours on finite random networks［J］.Physica A，2010，389(3):561-576.

［15］ZHANG Y，ZHOU S，ZHANG Z，et al.Rumor evolution in social networks［J］.Physical Review E，2013，87(3):032133.

［16］ALBERT R，BARABÁSI A L.Statistical mechanics of complex networks［J］.Review of Modern Physics，2002，74:47-97.

［17］卞曰瑭，何建敏，庄亚明.基于主体内禀特征的股市投资网络模型及鲁棒性研究［J］.管理工程学报，2013(1):108-113.

［18］BARRAT A，BARTHÉLEMY M，VESPIGNANI A.Weighted evolving networks:Coupling topology and weight dynamics［J］.Physical Review Letters，2004，92(22):228701.