基于刚柔耦合技术的PK 型工业多楔带横向振动仿真分析

李占国，史尧臣，陈乃熙

(1.长春理工大学 机电工程学院 长春130022;2.长春大学 机械与车辆工程学院，长春130022)

0 引言

由于多楔带具有结构紧凑、挠曲性好等优点，被广泛应用在工业传动系统中，多楔带传动过程中由于带与带轮的接触冲击会使带产生横向振动，导致带与带轮之间的相对滑动，并使带楔侧面产生磨损，影响了带的使用寿命和承载能力。

为了降低多楔带传动过程中的振动，国内外学者进行了一系列研究，2003 年，Kong 和Paker 将多楔带传动简化为伯努利－欧拉梁，建立了梁耦合振动数学模型，并对该模型进行了求解［1］。2008 年Zhu 等建立了多楔带三轮传动数学模型，分析了多楔带的振动特性［2］。2009 年上官文斌对多楔带的传动系统建模及带段横向振动控制进行了研究，将带简化为轴向运动弦，计算时应用Garlerkin 法计算了多楔带附件驱动系统的动态特性［3］。清华大学侯之超等人针对发动机附件传动系统固有振动特性，提出了一种计算固有频率的特征行列式约化算法［4］。

本文针对PK 型工业多楔带建立了带横向振动的数学模型，并求解了转速和张紧力对带横向振动的影响规律。基于刚柔耦合技术建立了PK 型工业多楔带横向振动仿真分析模型，通过仿真验证了所提出的多楔带传动过程中横向振动的计算方法，对多楔带传动系统的设计有一定的参考价值。

1 PK 型多楔带横向振动数学模型的建立

多楔带传动系统中在带与带轮接触处，由于带与带轮的接触冲击作用使带产生垂直于运动方向冲击激励，冲击激励以波的形式沿着带进行传递，使带在传动过程中产生的横向振动w(x，t)，以多楔带与主动轮楔入点为坐标原点，与带的运动方向反向为x 轴，以垂直与带竖直向上为y 轴，如图1 所示:

设带的轴向运动速度为c，张紧力为F，两带轮之间的中心距为L，多楔带的横截面积为A，线密度为m，弹性模量为E，截面惯性矩为I，多楔带的横向振动的位移为w(x，t)，t 为时间，则轴向运动梁的横向振动的微分方程:

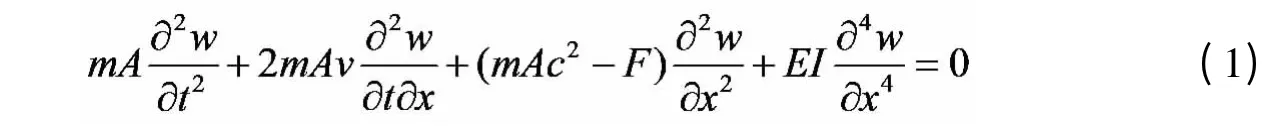
图1 轴向运动的梁模型

由于张紧力作用，带在包角内并不会产生振动，则边界条件为:

应用三角函数的Galerkin 截断方法对方程(1)进行离散化处理可得:

应用Runge－Kutta 法对方程(3)和(4)进行求解。设置PK 型多楔带弹性模量E=3000MPa，带长L=0.998m，横截面积A=0.000062m2，线密度ρ=91kg/m，主、从动轮直径d1=96mm。当张紧力为420N 时，转速为800rpm～1600 rpm 的横向振动曲线如图2 所示，当转速为1000 rpm 时，张紧力为320N、420N、520N 的横向振动曲线如图3 所示。从图2 中可以看出当主动轮转速为800rpm 时带的横向振动幅值为0.06mm，振动频率为6Hz，当主动轮转速为1200rpm 时带的横向振动幅值为0.02mm，振动频率为99Hz，即随着转速的提高，多楔带的横向振动幅值逐渐减小，但横向振动频率逐渐增加。从图3 中可以看出当张紧力为320N 时带的横向振动幅值为0.04mm，振动频率为9Hz，当张紧力为520N 时带的横向振动幅值为0.02mm，振动频率为9Hz，随着张紧力的增加，多楔带横向振动振幅减小，但横向振动频率不变。

图2 不同转速下的横向振动曲线

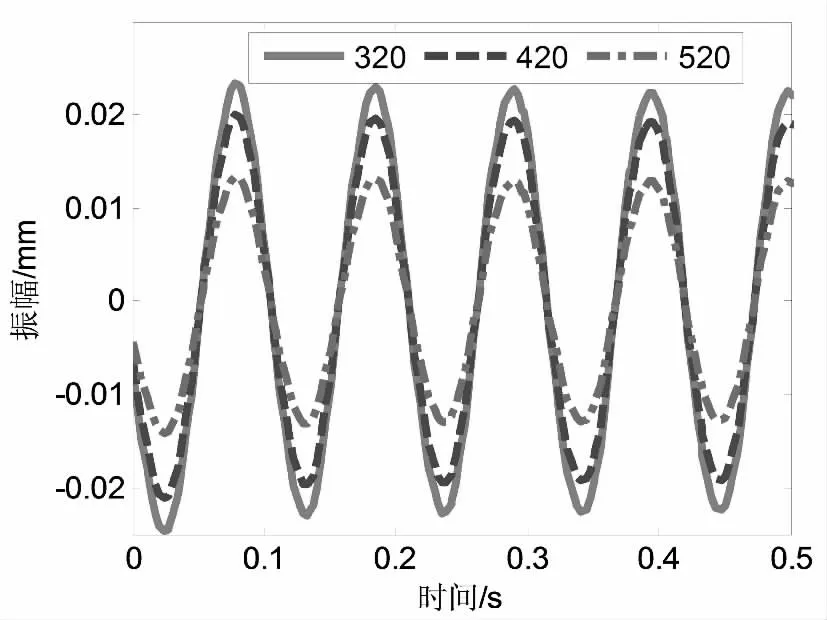
图3 不同张紧力下的横向振动曲线

2 PK 型多楔带横向振动仿真分析

2.1 刚柔耦合仿真模型建立

本文按照工业多楔带的国家标准GB/T 16588－2009，工业多楔带截面形状，选取4PK998 型多楔带和P4PK96 型多楔带轮进行仿真，利用catia 建立PK 型多楔带传动模型，并利用HYPERMESH 对多楔带进行网格划分，将带与带轮的模型导入多体动力学软件RecurDyn 中，如图4 所示。设置多楔带的线密度为91kg/m，弹性模量为3000MPa，泊松比为0.4;主、从带轮材料为45#钢。按照多楔带传动过程中的实际工况，定义主动带轮转速为1000rpm，带与带轮之间的刚柔接触，从动轮施加19.79N·mm 的传动负载扭矩。

图4 工业多楔带传动模型

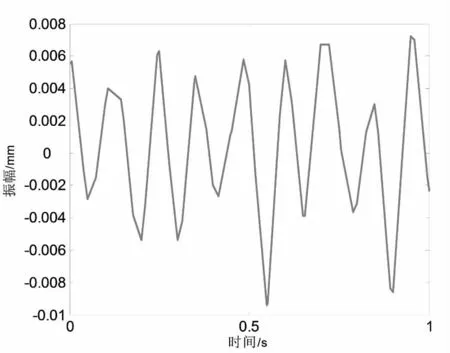
图5 带中点横向振动位移曲线

2.2 仿真结果及数据分析

2.1.1 多楔带中点的横向振动分析

对带体施加张紧力420N，主动轮转速1000rpm，设置仿真时间为1s，仿真步长为1000。得出带紧边中点处的横向振动位移曲线如图5 所示，可以看出带中点处的横向振动曲线承周期性变化，最大振动幅值为0.014 mm，振动频率为8.5Hz。

2.1.2 转速对多楔带横向振动的影响分析

当张紧力420N，主动轮转速为800rpm、1200rpm、1600rpm 时。通过仿真得到带紧边中点横向振动曲线如图6 所示，当主动轮转速为800rpm 时，最大振幅为0.2mm，频率为6Hz;当主动轮转速为1200rpm 时，最大振幅为0.15mm，频率为7Hz;当主动轮转速为1600rpm 时，最大振幅为0.05mm，频率8Hz。可以看出随着转速的增加，多楔带的横向振动幅值减小，横向振动频率增加。

2.1.3 张紧力对多楔带横向振动的影响分析

设置主动轮转速为1000rpm，对多楔带分别施加张紧力为320N、420N、520N，分析张紧力的改变对带中点横向振动的影响，如图7 所示。当张紧力为320N 时，横向最大振幅为0.05mm，频率为8Hz;当张紧力为420N 时，横向最大振幅为0.02mm，频率为8Hz;当张紧力为520N 时，横向最大振幅为0.01mm，频率为8Hz。由实验数据可以得出多楔带的横向振动振幅随着张紧力的增加而减小，而张紧力的变化不改变横向振动的频率。

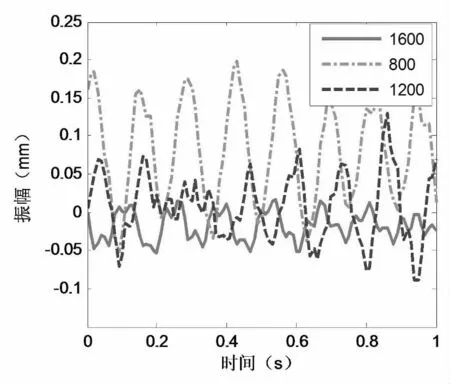
图6 不同转速下的横向振动曲线

图7 不同张紧力下的横向振动位移曲线

3 结语

本文针对PK 型工业多楔带，采用轴向运动梁模型建立了带传动过程中的横向振动方程，通过Runge－Kutta 法求解了带传动过程中紧边中点的横向振动位移曲线，并分析了转速和张紧力对带横向振动幅值和频率的影响关系，基于刚柔耦合技术建立了PK 型工业多楔带仿真分析模型，通过仿真分析验证了所建立的多楔带横向振动计算方法，为基于减振降噪的多楔带横向振动设计提供了理论基础。

［1］ Kong L，Parker R G.Equilibrium and belt－pulley vibration coupling in serpentine belt drives［J］.ASME Journal of Applied Mechanics，2003，70(5):739－750.

［2］ Zhu F，Parker R.Non－linear dynamics of a one－way clutch in belt－pulley systems［J］.Journal of Sound and Vibration，2005，279(4):285－308.

［3］ 上官文斌，张智，许秋海.多楔带传动系统轮－带振动的实测与计算方法研究［J］.机械工程学报，2011(2)1:28－36.

［4］ Hou Zhi－chao，Lao Yao－xin，Lu Qiu－hai.Sensitivity analysis and parameter optimization for vibration reduction of undamped multi－ribbed belt drive systems［J］.Journal of Sound and Vibration，2008，317(3):591－607.

［5］ 李占国，刘启龙，史尧臣，等.汽车发动机附件系统用多楔带传动平稳性仿真分析［J］，长春大学学报，2015(2):17－20.