基于效用函数法的包递交率指标效用函数构造
陈植林,蔡晓霞,陈 红
(电子工程学院,合肥 230037)
基于效用函数法的包递交率指标效用函数构造
陈植林,蔡晓霞,陈 红
(电子工程学院,合肥 230037)
包递交率是评估网络效能以及网络干扰效果的重要指标之一,用包递交率的测量值直接评估网络性能会使评估结果不够准确,因此对单项指标的测量值评价很重要。通过对一个简单的Ad hoc网络进行丢包测试,分析单次传输的丢包率与整体网络的包递交率关系,根据包递交率的变化对网络的影响,构造评估包递交率单项指标的效用函数。
网络评估;Ad hoc网络;效用函数评价法;包递交率;
0 引 言
战术互联网干扰效果评估指标有很多,需要用到多指标体系下的评估方法。多指标评估方法有很多,如层次分析法(AHP)[1]、武器系统效能工业界咨询委员会方法(WSEIAC法)[2]、TOPSIS法[3]、效用函数综合评价方法[4]等。
对于多指标综合评价,非常简单的思想是:将多个评价指标进行同度量化,然后再按照一定的合成模型加权求得总评价值。合成模型的权重系数一般采用层次分析法确定[5],指标的合成模型加权方式一般采用幂平均法或混合法[4],多指标体系下的各指标同度量化一般采用效用函数评价方法。采用效用评估法对多个指标进行同度量化时,需要对每个指标进行具体分析,分别构造合适的效用函数。包递交率是反应网络数据通信质量的重要指标之一,本文主要采用效用函数法对评估战术互联网干扰效果的包递交率指标的效用函数构造进行分析研究。
1 效用函数评价方法简介
效用函数评价方法称为“效用函数平均法”或“效用函数综合评价法”。写成一般公式为:
F=ξ(fi(xi),wi),i=1,2,…,p
(1)
式中:wi为单项评价指标xi的权数;fi(xi)为xi的效用函数评价值,也称“无量纲化值”或“同度量化值”。
在综合评价指标体系、权值wi、合成模型(即ξ)已经确定的情况下,效用函数评价法的关键就是单项评价值的确定(即fi的确定)。
2 构造效用函数的基本原则
对网络评估的指标进行无量纲化处理时,为了降低计算复杂度,可以直接对指标的测量值进行归一化处理。一般的归一化变换公式为[6]:
(2)
或:
(3)
式中:yi为归一化后的值;xi为指标i的原始测量值;xmax、xmin为指标i的取值上下限。
公式(2)为效益型指标的归一化公式,公式(3)为成本型指标的归一化公式。公式(2)和公式(3)中xi与yi为线性对应关系。从广义上来说,把指标的测量值归一化函数属于直线型效用函数,也是效用函数评价法中构造效用函数的一种。但是在实际评估中对单项指标的评价值与原始值可能不是线性对应的关系。如果简单地把指标作归一化处理,那么最后得出的评价结果会出现偏差。为了获得更为准确的单项指标评价值,需要用到不同类型的函数进行效用函数的构造。
效用函数的形式有许多种,按照二阶导的曲线特性可分为上凸型、下凸型、正/反S型、直线型。图1所示的几种曲线类型为递增型函数,对于逆指标只要稍作变换就可以得到相应的递减型函数。
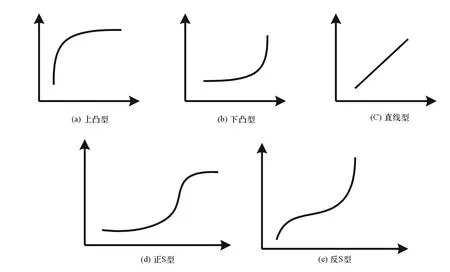
图1 效用函数的基本类型
构造无量纲化函数要注意以下几点[4]:
(2) 每个指标所对应的yi区间明确且相同,即用于评估的效用值应该具有明确且一致的取值范围或临界点。
(3) 无量纲化函数的类型及形式的选择应该根据评估指标正/逆贡献值的变动来决定。
(4) 当无法准确地确定无量纲化函数时,可以选择一些测试点拟合出所需函数。
(5) 每个评估指标的度量单位、取值范围、正/逆贡献值有所不同,所以对于不同的指标应该对其构造相应的无量纲化函数,不宜在同一指标体系中采用同一种。
(6) 对于有些指标的无量纲化函数,可能无法用一种函数拟合而成,可以采用分段的方式解决。
(7) 构造无量纲化函数时,应该为下一步多指标综合评估合成计算作考虑。如果构造出的函数无法用作多个指标的合成计算,那么该函数也就失去了构造的意义。比如,用幂平均函数合成指标的话,必须要求无量纲化函数的取值区间大于零,否则将无法计算。
(8) 理论上应该选择最精确的构造方式对指标进行量化,但实际运用中很难做到,因为通常只能根据对不同指标的要求判断其大致的评价值,所以构造无量纲化函数时,一般选择大致的函数类型进行构造。即构造出的无量纲化函数实际上也是一种“模糊量化”的方式。再加上采用效用函数对指标量化的过程比较复杂,且人为主观的影响占主要成分,所以在构造无量纲化函数时,一方面要注重其“精度”,再一方面要注重实用性以及简易性。
3 包递交率效用函数的构造
包递交率效用函数的构造过程如下:
(1) 确定是以评估攻击效果为目的对网络的包递交率构造效用函数,则包递交率应该是逆指标,效用函数应该选取递减型函数;
(3) 选取合适的测试点。对于包递交率指标而言,设对网络施加干扰(或实施攻击)后,包递交率为xb_max以上时,网络通信不受太大影响,干扰(或攻击)无效,对干扰(或攻击)评价的效能值为yb_min;包递交率为xb_min以下时,网络通信基本瘫痪,干扰(或攻击)完全有效,对干扰(或攻击)评价的效能值为yb_max;
(4) 采用分段函数的方式把测试点相连,得出粗略的评估包递交率效用函数:
(4)
(5) 由于评估指标还有很多,采用分段函数构造出的效用函数无法直接带入综合评估模型的合成公式中(如幂合成法的公式),不利于后期综合评估时的计算。所以,在用测试点描绘出分段函数后,应尽可能地用一个函数对其进行“模糊匹配”。如上述步骤4)中的分段函数呈Z型,所以构造效用函数时可以用反S型函数进行合成构造。应用比较广泛的S型基本函数有Logistic函数和Sigmoid函数,在统计学中,一般采用Sigmoid函数作为基本合成函数。根据基本函数的变换特性,构造评估包递交率的效用函数为:
(5)
式中:系数100表示百分制;a、b为常数,为尽可能地使构造函数表示得更加准确,应选取合适的常数a、b,使函数值尽可能地与测试点相吻合。
文献[7]中给出了Adhoc战术通信网的包递交率效用函数。但是该文献在确定效用函数的系数时没有针对具体情况,只是用“假设”的标准来构造的。对网络的评价需要建立在严格的计算与测试的基础上。
接下来本文通过仿真,先定性分析数据传输时包递交率的改变对网络性能的影响,并根据分析给出包递交率指标的量化效用函数。
4 包递交率指标的测量方式
包递交率是衡量网络节点间数据是否能正常交互的重要指标。根据统计方式的不同,对包递交率的描述可分为2种:确定性包递交率和概率性包递交率。
确定性包递交率侧重于评价网络的实时数据传输性能,一般选取观测网络运行的一个时间段内,成功接收的数据包与发送的总数据包数量之比,统计方式如下:
(6)
式中:Pb为确定性包递交率;Nbr(T)为t∈[t,t+T]时段内成功接收的数据包总数;Nbs(T)为t∈[t,t+T]时段内发送的数据包总数。
概率性包递交率侧重于评价网络对业务处理的连续性,一般选取网络运行的一个时段内,交互的数据包能够满足业务需求条件的概率,统计方式如下:
(7)
式中:Pb′为概率性包递交率;T为统计网络运行的时间段周期;TNb为t∈[t,t+T]统计时段内,交互的数据包能够满足业务需求条件的时间。
对网络性能及干扰效果进行理论分析时,所用到的包递交率比较偏向于反映网络数据传输的性能。一般情况下,网络干扰效果评估指标体系中,包递交率被算作数据传输性能的下级指标[8],因此本文选取确定性包递交率作为评估指标。下文中的包递交率指的都是确定性包递交率。
5 仿真分析
本文采用NS-2(NetworkSimulator2)进行仿真,选取一个较为简单的Adhoc网络模型,具体仿真网络环境及参数设置如下:
节点个数:50 个;最大联机数:20;联机时长:随机。
节点移动速度:6~8m/s;节点暂停时间:60s; 场景大小:2 500m×2 500m。
数据流:CBR数据速率:16kb/s信号传输:TwoRayGround模型。
路由协议:DSR路由协议MAC层协议,802.11b协议协议参数均为缺省值。
为了模拟网络受扰时网络性能下降的情况,本文用NS-2的ErrorModel模型使数据传输时产生固定概率的丢包现象来分析受扰后的网络性能,根据网络性能的变化分析效用函数参数的选取。
仿真结果如图2所示,横坐标表示设置ErrorModel中节点的丢包率参数,纵坐标为统计后整体网络的包递交率,“Delivery_0”表示不用ErrorModel情况下的网络性能指标值,“Delivery_50”表示设置50个节点丢包情况下网络性能的指标值。由于本文仿真时采用的干扰模型中错误分布随机参数每次取值不同,可能会导致每次仿真结果不同。图1~图3中所有点均测试3次以上,其中折线处及折线处临近2点仿真5次,取平均值作为最终结果。
5.1 对仿真结果的定性分析
包递交率与网络被干扰程度的关系如图2所示。
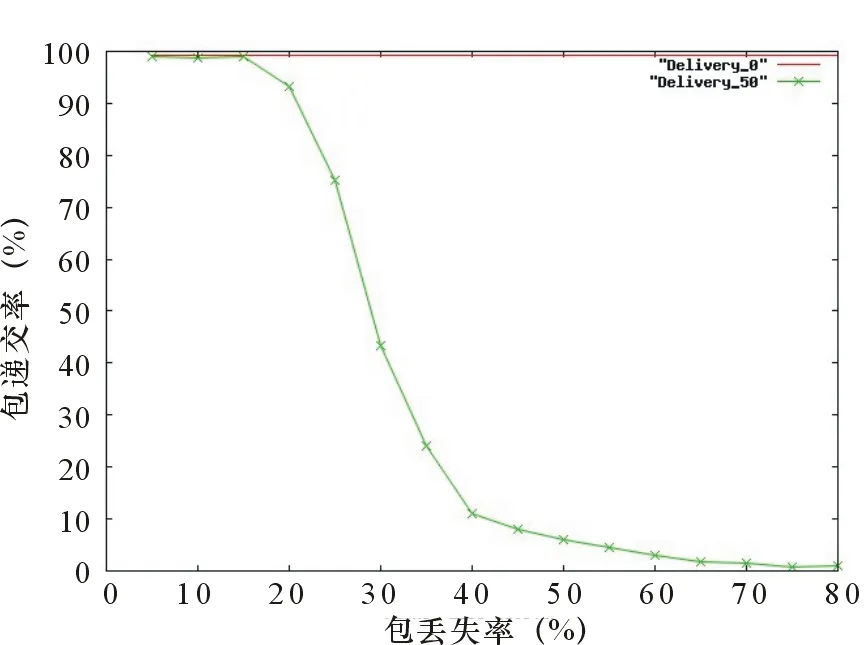
图2 包递交率与网络被干扰程度的关系
当受扰节点数较少或受干扰节点接包错误率较低时,整体网络所受影响较小。图1中显示,即使所有节点接包错误率为10%,网络表现出的包递交率依然可以保证节点间通信。受错误重传机制的影响,本文仿真设置最大重传次数为7,如果节点接收错误率为10%,数据包经多次重传后的实际错误率应为10-7。
包递交率整体趋势随着受扰节点数与节点受扰程度的增加而增加。多次重传数据导致信道竞争加剧、路由消息泛洪,造成网络阻塞。当MAC层队列达到最大值时,接收端接收的包(包括数据包和路由包)被迫丢弃,重传次数达到上限的数据包直接被发送端丢弃,网络中数据碰撞及路由消息泛滥产生的连锁反应使网络包递交率迅速下降,网络质量直线下滑。
5.2 包递交率指标效用函数的确定
通过4.1节的分析可知,对本文所建立的仿真网络环境来说,当丢包率在15%以下时,反映整体网络性能的包递交率、平均端到端延迟、路由开销3项指标都正常;当丢包率大于15%时,网络整体性能开始严重下降;当丢包率大于30%时,整体网络的包递交率不足10%,延迟超过4s,路由开销也很大,网络基本处于瘫痪状态。通过以上分析,所以构造包递交率的效用函数选取的测试点为(0.8,60),(0.65,85),构造的效用函数为:
(8)
用MATLAB作图后得到的相应曲线如图3所示。
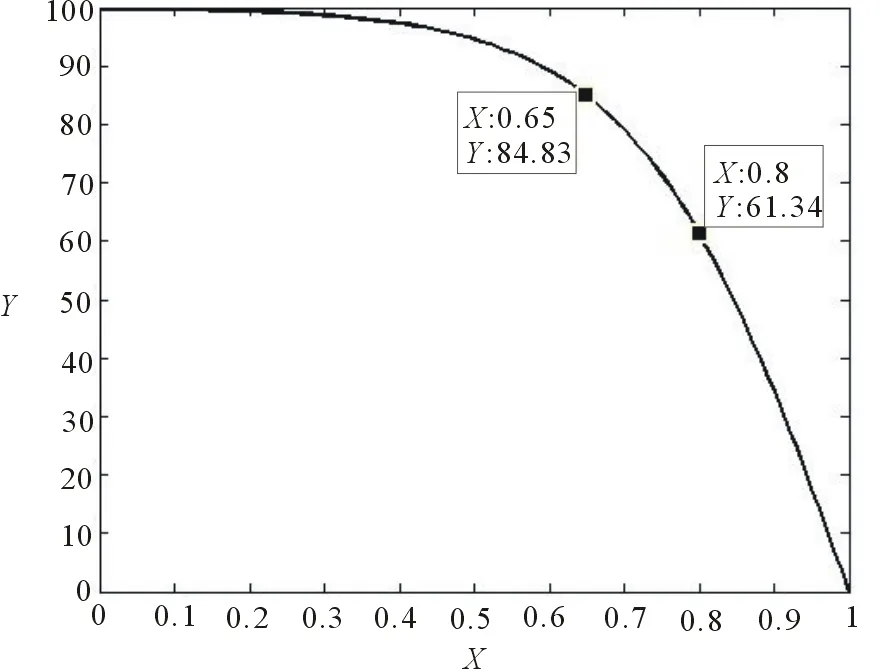
图3 第1种包递交率效用函数曲线图
由图4所示的包递交率效用函数曲线图可得出与测试点最接近的2点为(0.8,61.34),(0.65,84.83)。但是图4所构造的效用函数还是存在不足。因为当丢包率在15%以下时,网络所表现出的包递交率、延迟等指标几乎不受影响,网络性能良好,所以构造的效用函数在评估干扰效果较差的干扰方式时一定程度上无法准确地评估干扰效果,从而影响评估的公正性。导致这种情况发生的主要原因是测试点选取在函数区间的中间位置,在进行函数构造时没有考虑函数区间两端的最值问题。
针对以上情况,选取函数极值作为测试点。选取极值测试点为(60,100)、(85、0),构造的效用函数为:
(9)
构造函数曲线如图4所示。
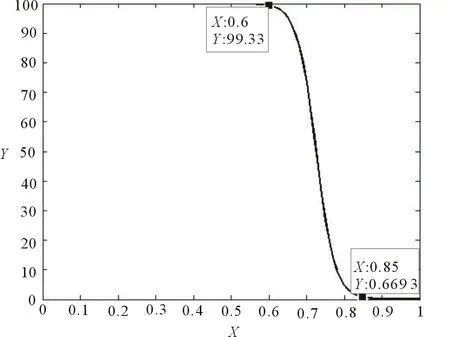
图4 第2种包递交率效用函数曲线图
由图4所示的包递交率效用函数曲线图可得出,与测试点最接近的2点为(0.85,0.669 3),(0.6,99.33)。不过这类函数还是存在不足。当丢包率达到15%以上时,网络性能下降非常迅速,但是,在x=0.8附近时,函数的二阶导特性为负,呈凹函数的特点。当丢包率大于15%时,评估值应该迅速上升,而该函数在x∈(0.725,0.9)区间内的评价值随x的减少增加过慢。相比于前文取的(0.8,60),(0.65,85)2个测试点,该函数取值为(0.8,4.743),(0.65,95.26)。显然这2点的取值与主观判断的评价差别还是很大的。
构造出的效用函数(8)、(9)与选取的测试点之间存在一定的误差,如果要构造更高精度的效用函数还需要更改公式参数,或是选取其它的基本函数来构造。公式(8)、(9)所示的效用函数只取了2个测试点进行构造,要构造更高精度的效用函数需要选取更多的测试点。如果选取前文叙述的4个测试点进行函数构造可能无法用1个函数表达,必须采用分段函数的表述方式。但是,本文选取的测试点带有笔者一定程度的主观判断,而且效用函数量化方法本身就是一种“模糊量化”的方式。构造效用函数时,无法保证绝对客观地选取测试点,并且即使选取的参数与测试点完全吻合,也不能保证其它点的评价标准就是完全正确的。正如前文叙述的那样,构造效用函数时,一方面要注重其精度,再一方面要注重实用性以及简易性。
6 结束语
包递交率是评估网络性能以及网络干扰效果的重要指标之一。为了更好、更准确地对网络性能或干扰效果进行评估,需要对包递交率的指标测量值进行进一步评价。本文的主要工作是对一个简单的Adhoc网络进行丢包测试,分析节点间的丢包率与整体网络的包递交率关系,评估包递交率与网络性能之间的关联,为建立包递交率效用函数建立理论基础。通过分析选取适当的测试点,确定函数参数,建立了2种不同的包递交率效用函数。
[1] 卢紫毅,范建华.基于层次分析法的这战术通信网络效能评估[J].现代电子技术,2011,34(1):57-60.
[2]LiW,MaoN,PanW.TheEffectivenessevaluationmodelofradarjammingsystembasedonWSEIACmodel[A].CCDC[C].Shenyang,China,2008:1848-1852.
[3] 周亚,多属性决策中的TOPSIS法研究[D].武汉:武汉理工大学,2009.
[4] 苏为华.多指标综合评价理论与方法问题的研究[D].厦门:厦门大学,2000.
[5] 刘进,王永杰,张义荣,等.层次分析法在网络攻击效果评估中的应用[J].计算机应用研究,2005(3):113-115.
[6] 蓝元沛,孟庆春,李峰,等.基于多属性效用理论的飞机设计选材方法[J].航空材料学报,2010,30(6):88-94.
[7] 范会杨.Adhoc战术通信网效能评估模型与方法[D].成都:电子科技大学,2013.
[8] 杨红娃,战场网络攻击效能评估技术[J].通信对抗,2006(1):24-28.
Utility Function Construction of Package Delivery Rate Index Based on Utility Function Method
CHEN Zhi-lin,CAI Xiao-xia,CHEN Hong
(Electronic Engineering Institute,Hefei 230037,China)
Package delivery rate is one of important indexes to evaluate network efficiency and network interference effect.Using the measured value of the packet delivery rate to evaluate network performance directly may make the evaluation result not accurate,so it is important to evaluate the measured value of the single index.Based on packet loss test to a simple Ad hoc network,this paper analyzes the relationship between the packet loss rate of single transmission and the package delivery rate of overall network,constructs an utility function to evaluate single index of package delivery rate according to the influence of package delivery rate change on the network.
network evaluation;Ad hoc network;utility function evaluation method;packet delivery rate
2015-03-12
TP393
A
CN32-1413(2015)04-0097-05
10.16426/j.cnki.jcdzdk.2015.04.025

