快速成型的STL模型切片轮廓优化新方法
周惠群,吴建军
ZHOU Hui-qun, WU Jian-jun
(西北工业大学 现在设计与集成制造技术教育部重点实验室,西安 710072)
0 引言
快速成型是一种基于离散累加的先进制造技术,近年来得到了非常迅猛的发展。其基本过程是首先对零件的CAD模型进行分层处理,得到零件的二维截面数据,然后根据每一层的截面数据,以特定的方法生成与该层截面形状一致的薄片,这一过程反复进行,逐层累加,直至生长出零件的实体模型。也就是说,在快速成型的加工过程中,CAD模型必须经过分层处理才能将数据输入到相应的加工设备中,因此可以说分层处理是快速成型的核心,所以该问题一直是该领域的研究热点[1,2]。
针对CAD模型的分层,国内外相关的研究人员提出了各种分层算法,主要可以分为基于CAD模型的直接分层和基于STL模型的分层这两大类算法。在快速成型技术的早期,普遍采用由美国3D System公司提出STL文件来表示CAD实体模型。虽然STL文件有种种不足和缺陷,但目前仍然是CAD模型转化成快速成型数据的主要来源。而在众多的分层算法中,基于STL模型的分层算法依然是研究的主流[3,4]。
由于STL文件是对CAD模型表面用一系列小三角形面片进行近似而得到的,这使得在快速成型加工中截面轮廓含有大量的冗余微小线段,这些线段必然影响加工过程的平稳性和效率。为了提高加工精度和速度,对这些微线段轮廓进行优化处理成为研究人员必须面对的问题。在此基础上,文献[5]提出采用计算曲率的方法,文献[6]提出了限定三角形高度的方法等等。本文在总结前人的基础上,提出了一种数据冗余点去除的新算法——基于截面轮廓三角形面积及其累加误差的计算方法,该方法可以在保证加工精度的条件下,有效地去除了冗余点。
1 STL文件及STL模型切片
1.1 STL文件
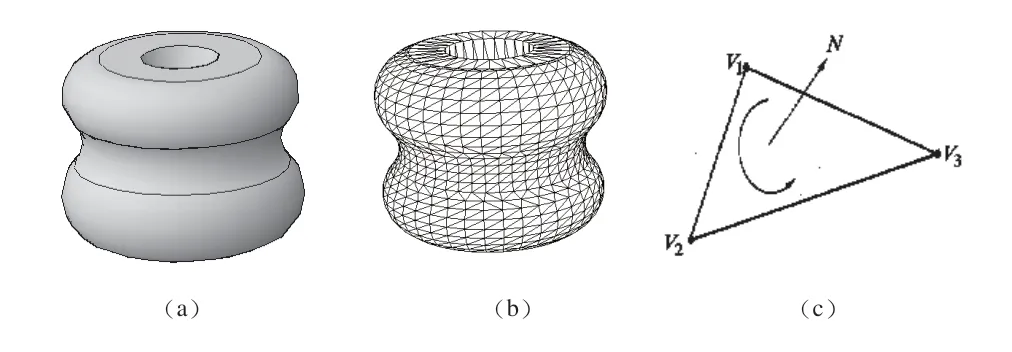
图1 CAD模型、STL模型及三角形面片的示意图
如图1(a)、(b)、(c)所示分别是零件的CAD模型图、STL模型图和单个三角形的3个顶点坐标及三角形面片的法向量示意图。STL文件是若干空间小三角形面片的集合,每个三角形面片用其三个顶点和指向模型外部的三角形面片的法向量组成。STL文件的大小(即三角形数量)与产生该文件时对其要求的精度有关。当STL模型对CAD模型的近似程度(即精度)较高时,用来近似零件表面的三角形面片数目较多,反之则较少。关于STL文件格式的文献很多,这里不再赘述。
1.2 STL模型切片
快速成型加工的预处理是先建立零件的CAD模型,然后将此模型转化成STL模型,在STL模型上指定一个分层方向(一般为Z轴),沿着分层方向每隔一定距离用垂直于Z轴的平面P进行切片处理,再把所得到的截面轮廓的微线段连接成封闭的轮廓线,即STL模型的截面轮廓。 换言之,分层就是用垂直于分层方向的截平面截交STL模型,这个截平面和STL模型的三角形相交,然后得到封闭的截面轮廓线。
当STL模型对CAD模型的近似程度较高时,因为三角形数目多,分层后得到的截面轮廓会有大量的微线段。而且,因为三角形共顶点及共边,在同一条直线段上还会存在多个数据点,在同一个数据点上也会有多个重合点。切片厚度根据零件的精度和成型机的有关参数确定,如果切片厚度小,成型精度高,但成型的效率低。
用平面P1、P2、P3去截交STL模型的情况如图2所示。从图2中可以看出,截交STL模型后得到的轮廓是由一条条微线段组成的封闭多边形,每个封闭多边形也就是一个加工区域环。一个截面轮廓可能含有多个这样的封闭环,在这些环里进行成型加工。根据切片原理和STL文件的特点可知,根据截交的位置不同,每个环都含有大量的微线段,有的在同一直线上,有的过于短小,短到小于加工精度,以至于根本无法进行加工。当截平面通过三角形面片的顶点时,还会出现重复点。而且这些微线段成为一种多余的信息,对加工过程造成了一定的影响和干扰。只有去掉这些微线段,才能提高加工的效率和稳定性。
如图2中的P1切片通过三角形顶点V1时,截交共此顶点的三角形T1、T2、T3、T4、T5、T6、T7、T8,根据不同的切片算法,则可能出现二重点或多重点,这些都会影响到后续的插补加工。

图2 STL模型的截交图
2 新算法的基本原理
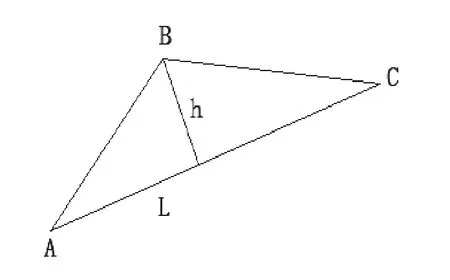
图3 三角形的面积计算
如图3所示,在三角形ABC(以下用ΔABC表示)中,当ΔABC的面积(即1/2×h×L)小到一定值时,该三角形就可以忽略。在三角形中,如果面积一定时,高h和底L是反比关系。A、B、C三个点中,总有一个点应该被忽略。即h较大时,L就较小;L较大时,h就较小。这样,通过求面积的方法,前述的各类冗余点就合并为一类了。设:

在STL模型被垂直于Z轴的平面截交以后,形成一个新的截面轮廓区域。该区域就是快速成型加工的扫描区域。它是由一系列直线段组成的,依次扫描各数据点,以连续的三点组成三角形,计算该三角形的面积(即1/2×h×L),如满足式(3),则该点作为多余点去除,然后以新形成的直线作为一条边,加入一个新点,形成一个新三角形,再计算该三角形的面积。依此类推,直到整个截面轮廓的数据点结束,这一层的数据优化过程也就完成了。下一层也如此进行,直到所有的轮廓层都计算完为止。
如图4所示,具体的截面数据优化过程如下:STL模型经过截交后的部分外轮廓为:{A,B,C,D,E,F},首先ABC组成一个三角形,其面积为1/2×(AC)×h1,若该值≤δ,则B点作为冗余点去除。然后再计算ΔACD的面积,若该值≤δ,依此计算ΔACE的面积,若该值再≤δ,再计算ΔACF的面积,直到三角形面积的值超过δ为止。
上述算法的最大问题就是累积误差。也就是说,当前一次有数据点去除时,新形成的边已经包含了该次优化的误差,在下一次新的三角形面积计算时,如不考虑前次的影响,将会产生误差累积,得到错误的结果。因此,完整的算法应该是:若前一次计算中有数据点去除,则本次计算时不仅要计算本次新形成的三角形面积,而且还应再加上次去除掉的三角形面积值,只有这个累加值满足式(3)的误差范围要求时,才能去除这一点。以此类推,完成计算的全过程,扫描完各个STL模型的截面轮廓后,分层数据的优化也就完成了。从这个数据点的去除过程可以看到,一切都是在截面轮廓的精度范围内进行。因此,数据优化后的截面轮廓与原轮廓的误差完全控制在精度范围内。
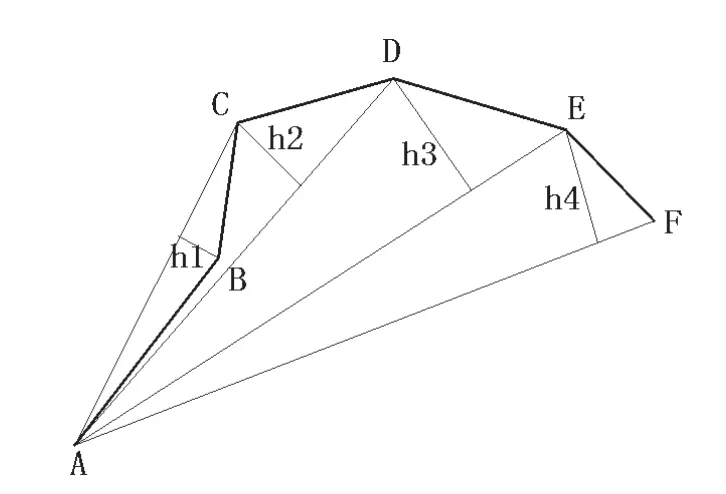
图4 截面数据优化过程

图5 实例零件的截面轮廓
3 新算法的过程描述
在快速成型加工的前期,必须进行CAD模型的预处理。在CAD系统中创建CAD模型后,由于CAD系统自身含有将CAD模型转化成STL模型的功能,只须调用相关的转换命令即可将CAD模型转换成STL模型。然后依据快速成型制件的形状,确定分层切片的方向,将该方向设置一般设置为Z轴方向,再调用CAD系统的剖切命令,指定分层厚度后,用垂直于Z轴的平面去对STL模型进行分层,可以得到STL模型的分层轮廓。这时,就可以运用上述的方法对STL模型的截面轮廓的数据进行数据优化了。
STL模型的截面轮廓的数据优化可以描述为如下的过程:


4 实例验证
如图5所示是一个零件的STL模型的截面轮廓,未经过优化时共有数据点632个。在经过使用本算法进行冗余数据的处理之后,还有数据点298个,数据点的数量只有原来的47%。由此可见,本算法确实能够减少STL模型的截面轮廓的数据量。在满足制件加工精度的基础上,提高了快速成型的加工效率。
5 结论
三维CAD实体模型的分层切片处理是实现快速成型加工的必由之路。在目前的快速成型制造中,尽管STL模型有很多不足和缺陷,但在众多的分层方法中,针对STL模型的分层方法仍然是快速成型技术研究的主流。由于快速成型加工中所采用的STL文件格式的特点,决定了STL模型的截面轮廓必然由一系列微线段构成,并且含有大量的数据冗余点,肯定会影响后续的数据处理以及快速成型加工的过程。
本文在总结目前对STL模型进行切片以后轮廓数据优化方法的基础上,提出了一种新的STL模型切片轮廓数据优化的新算法—基于截面轮廓三角形面积及其累加误差的计算方法,详细阐述了本算法的基本思想和运算过程。实践证明,采用本算法进行数据优化以后,在保证加工精度的基础上,每一层的数据点减少一半以上,不仅减少了加工过程的数据处理量,而且还能提高加工效率,同时也有利于后续的扫描路径规划。
[1] Ali Kamrani, Emad Abouel Nasr.Rapid Prototyping:Theory and Practice[M],Springer-Verlag New York Inc.2006.
[2] 平雪良,高同军,孟凡虹.一种提高快速成形系统精度的新切片算法[J].机械科学与技术(西安),2008,27(9):1121-1124.
[3] 温佩芝,黄文明,吴成柯.一种改进的STL文件快速分层算法[J]. 计算机应用,2008,28(7):1766-1768.
[4] 赵吉宾,刘伟军.快速成形技术中基于STL模型的分层算法研究[J].应用基础与工程科学学报,2008,16(2):224-233.
[5] 黄新华,孙琨,方亮,岑启宏.STL模型的分层轮廓数据优化算法[J].机械科学与技术(西安).2004,23(5):605-607.
[6] 郭新贵,汪德才,刘亚东,李从心.快速成型的切片数据优化[J].制造技术与机床,2002,9(3):30-32.

