基于Mie散射理论的云红外辐射传输研究

陈 卫，方义强，施 展，邓 潘

(脉冲功率激光技术国家重点实验室，解放军电子工程学院，安徽合肥230037)

1 引言

在空中目标的红外探测中，云作为最主要的天空背景，将对目标探测产生极大的影响，不仅可能对目标的辐射造成遮挡，也可能造成目标探测的虚警。因此研究云的红外传输特性以及云的辐射特性具有重要的意义。

云粒子在8～14 μm波段具有强烈的 Mie散射［1］，对同样的波长，云的散射和消光要比气溶胶的大一到两个数量级以上［2］。不同种类云粒子的分布和特点不一样，因而其散射和消光呈现出不同的特点。在云散射问题上的研究方面，主要是通过Mie 散射理论［3－5］、射线跟踪法［6－7］、T 矩阵法［8－9］等来计算云粒子的散射特性，其中后面两种方法主要是针对卷云中冰晶粒子的非球形特征而引入的。Mie散射理论假设散射粒子为球体，具有较宽的几何实用性［10］。因为实际中云粒子是随机取向的，朝每个方向上的表面单元是相等的，它具有与球形粒子相同的表面单元角向分布，因此通过Mie散射理论来计算云粒子的散射具有实际意义。

2 云粒子分布规律

云是由大量细微的水滴或冰晶组成的悬浮在大气中的可见聚合体，云滴按大小的分布曲线，即云滴的谱分布，常用修正的Gamma函数分布表示［11］:

其中，a1是总的数密度;a2和a3是形状参数，是由观测资料确定的经验系数，r为云滴半径，不同种类云的系数不同，同种云不同位置的系数也不同。LOWTRAN中采用的几种典型云的粒子尺度分布模型参数如表1所示［11］。在计算云的散射时，除了粒子的分布特征外，另一个重要的量就是粒子的复折射率。水和冰在红外8～14 μm波段的复折射率(m=m1－im2)的试验值如表2所示［2，9，11］。

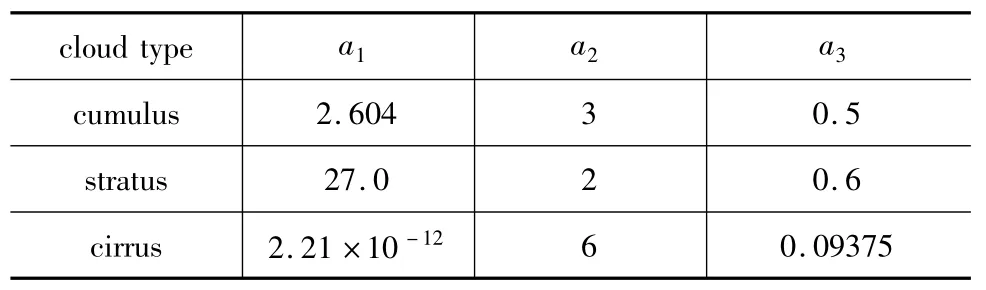
表1 典型云粒子尺度分布Tab.1 Particle size distribution of typical clouds

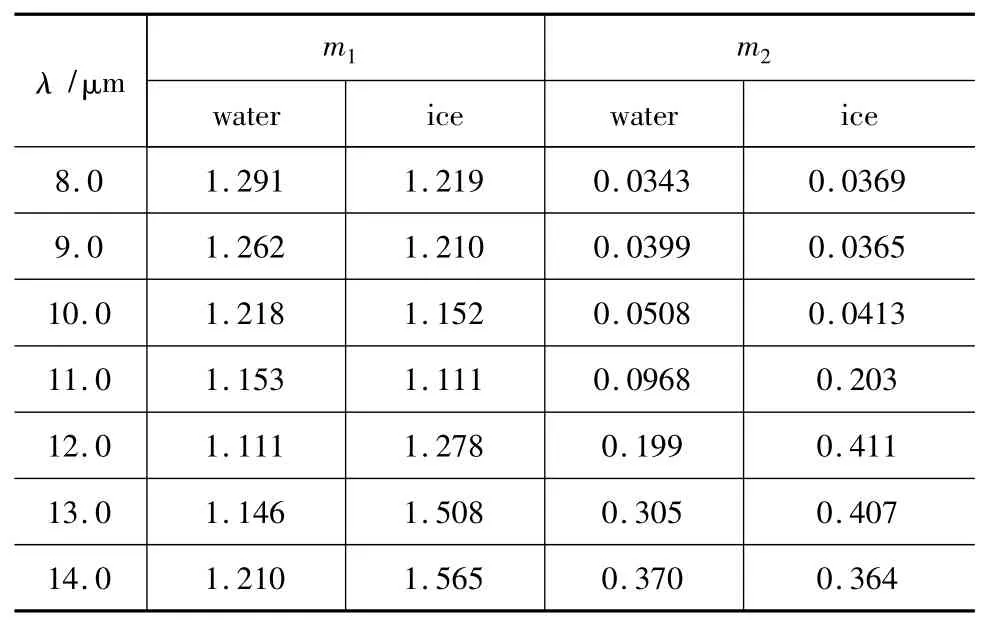
表2 水和冰的复折射率Tab.2 Complex refractive index of water and ice

3 Mie散射理论

根据Mie散射理论，Mie散射截面积Cs、消光截面积Ce的计算方法为:

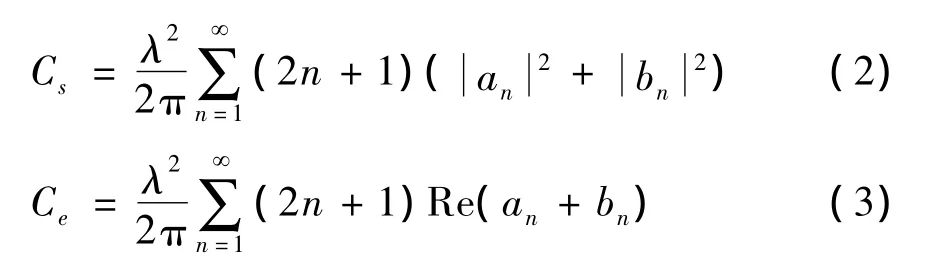
式中，λ为散射光波长;an、bn为Mie散射系数，其具体的计算可以参考文献［12］和［13］。

吸收截面积可表示为Cα=Ce－Cs。粒子的散射截面积与几何截面积πr2之比称为粒子的散射效率因子Ks［12］。

光在某个给定方向单位立体角中散射的能量与在所有方向上平均的单位立体角中的散射能量之比，称其为散射相位函数，散射相位函数同样可以通过前述的量计算得到:

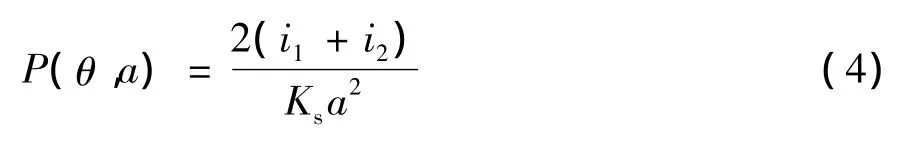
根据以上的推导计算公式，通过MATLAB计算了不同10 μm波长下不同粒径的散射方向图，图1所示依次为粒子半径为 1 μm、5 μm、10 μm、20 μm时的散射相函数方向图。

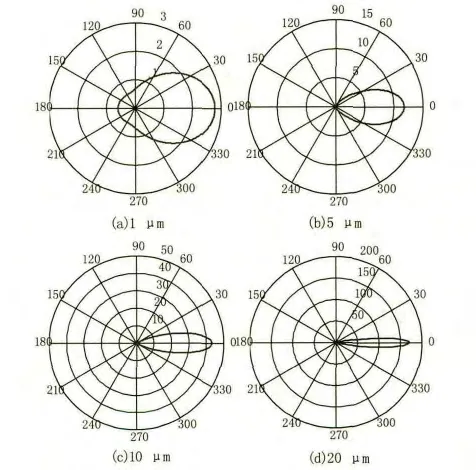
图1 不同粒径下的散射相函数方向图Fig.1 Scattering phase function pattern in different particle size

从图中可以看到对于一定的波长，粒子对光的前向散射随着粒子半径的增加而增大和锐化，而后向散射逐渐减弱。

以上的分析是针对单个粒子进行计算的，对于一粒子群，为了区分与单个粒子的区别，这里对粒子群的量加下标r来表示，其散射相函数的计算表达式为［12］:

其中，n(r)为粒子的半径分布函数，可进一步表示为:

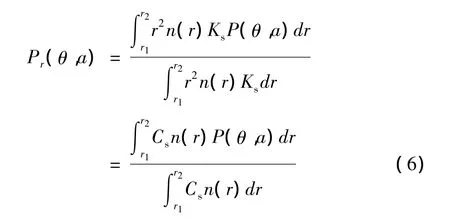
假设某一组单一粒子半径散射粒子的粒子数密度为Ns，则定义其散射系数为［10］:

那么对于非单一粒子半径散射粒子，可以求得其散射系数为:

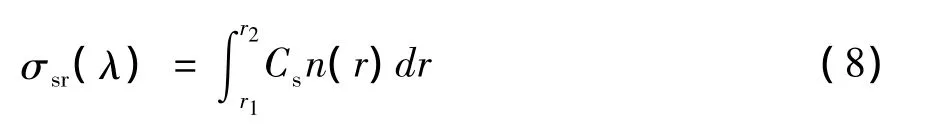
散射系数σsr的单位为m－1。

同样可以计算得到消光系数σer和吸收系数σαr。

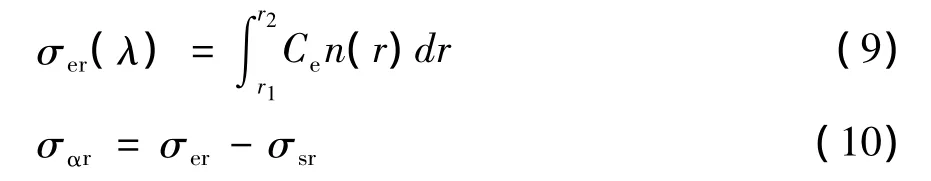
4 辐射在云中的传输

辐射经过云层传输到探测器的过程可用图2表示，图中假设目标完全在探测器的视场内，对探测器的张角为ΔΩ，云厚为d。

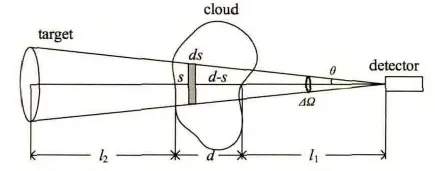
图2 辐射传输示意图Fig.2 A sketch map of radiance transfer

在云的s处，任意方向的散射强度可用相函数表示为［10］:

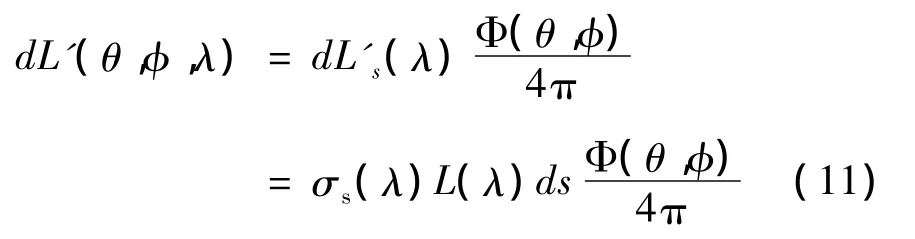
其中，L(λ)为入射的辐射亮度;dL's(λ)表示ds距离散射掉的部分。

辐射经过ds距离后的辐射亮度应为:

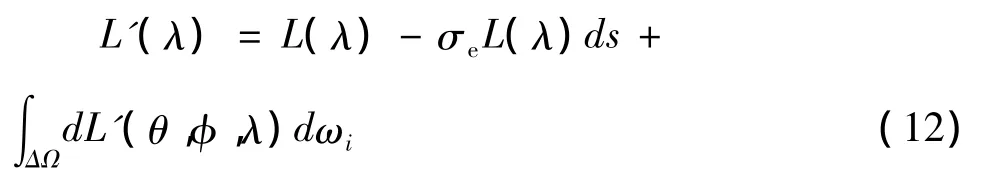
其中，减号项为消光而衰减的量，加号项为由于粒子的前向散射而增加的量。对式(12)整理并在d上积分可得:

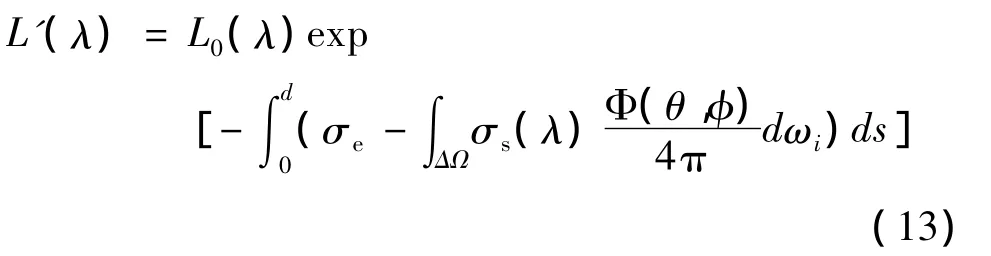
实际中张角ΔΩ一般很小，因此在一般的计算中将前向散射引起的增量省略，从而得到:

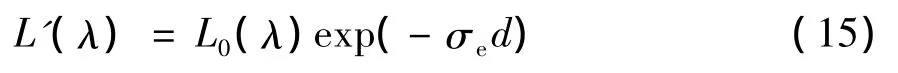
5 计算与分析

首先结合云粒子的粒径分布和相关的折射率分布，通过粒子群的Mie散射计算模型，计算得到了不同波长下积云的Mie散射相函数方向图。计算时粒子半径的积分范围为1～30 μm，计算结果如图3所示，图中曲线由外到内分别对应8～14 μm散射相函数方向图。从图中可以看到，不同波长处云粒子的散射相函数随着波长的变化较大。整体而言，粒子对入射光的前向散射随着波长的增大而减小，但是前向散射的宽度基本不变。而从变化率来看，在8～14 μm波段，前向散射减小的速度为先减小而后增大，最小值出现在10～11 μm 附近。

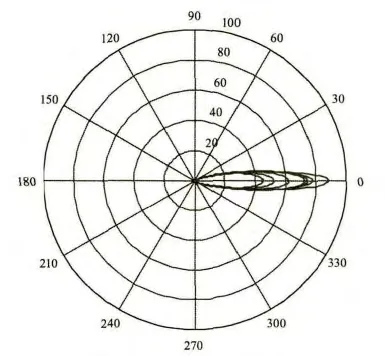
图3 积云的Mie散射相函数方向图Fig.3 The scattering phase function pattern of cumulus

根据前述的理论模型，计算得到的积云散射系数σs、消光系数σe、吸收系数σα和波长的关系如图4所示。从图中可以看到散射系数和消光系数均随着波长的增加而先减小后增大，最小值在12 μm附近，吸收系数整体上随着波长的增大而增大。另外，从曲线可以得出，在11～14 μm波段区间上，吸收系数大于散射系数，即在此波段内积云对光辐射的衰减吸收的作用大于散射的作用，而在其他波段散射的作用更大。

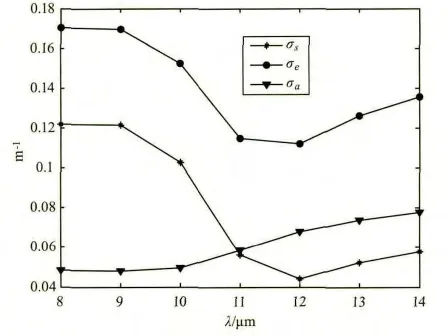
图4 积云的σs、σe和σα曲线图Fig.4 Graph of the cumulus’s σs，σeand σα

根据前面计算得到的消光系数，就可以计算辐射在云中的传输。采用式(15)的形式，假设辐射传输到距离d时其值衰减到初始值的0.1，那么计算得到的不同波长处的距离d如图5所示。根据计算结果可以看到，云将对8～14 μm波段产生极大的衰减，该波段内辐射衰减90%的距离d仅为10 m的量级，其中最小距离在8 μm处，为13.5 m，而最大的距离在12 μm处，也仅为20.5 m。结果表明，一个厚度为10～20 m的积云可以对目标8～14 μm波段的辐射造成几乎全部的遮挡。

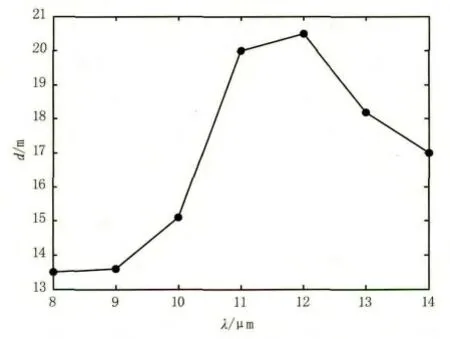
图5 积云d的曲线图Fig.5 graph of the cumulus’s d

同样的步骤，计算得到的层云和卷云的散射系数σs、消光系数σe和吸收系数σα以及相应使辐射衰减90%的距离d如图6～图9所示。其中层云按水云的折射率计算，卷云按冰晶粒子的折射率计算，卷云的粒子半径取值范围为10～200 μm。从计算结果来看，层云的衰减比积云小一半左右，那么相应的距离d约为积云的两倍;而对于卷云，其消光系数与积云和层云相比要小得多，因而其距离d也就相对大得多，达2130～2210 m的范围，说明卷云对8～14 μm波段的辐射衰减很小。

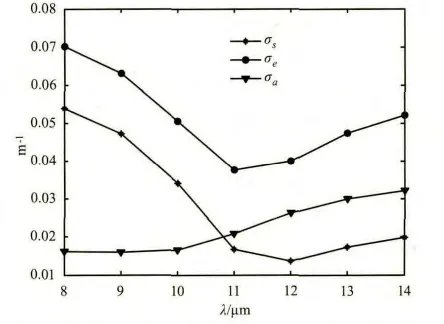
图6 层云的σs、σe和σα曲线图Fig.6 graph of the stratus’s σs，σeand σα

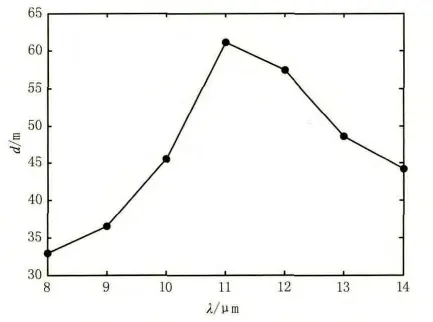
图7 层云d的曲线图Fig.7 graph of the stratus’s d

最后对前向散射对辐射传输的影响进行一下讨论和说明。在8 μm波长处通过式(13)计算了三种云的距离d，假设张角ΔΩ为5 mrad，通过计算发现，对于积云和层云，由于前向散射引起的误差在0.1%以内，因此可以忽略前向散射的影响。但是对于卷云，由于前向散射引起的误差为4.2%左右。这样的误差对于红外辐射的研究而言，完全在其允许的误差以内，因此可以忽略前向散射对辐射传输的影响。

图8 卷云的σs、σe和σα曲线图Fig.8 graph of the cirrus’s σs，σeand σα

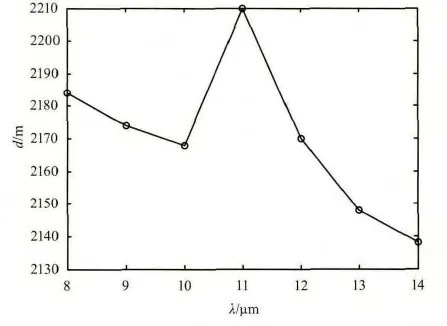
图9 卷云d的曲线图Fig.9 graph of the cirrus’s d

6 结论

文章在 Mie散射理论的基础上，对云在8～14 μm远红外波段的辐射传输特性进行了研究。通过计算三种典型云的散射系数、消光系数、吸收系数以及辐射衰减90%的距离可以得到:积云对该波段的红外辐射具有极大的衰减，20 m左右厚度的积云就可以对辐射造成几乎全部的吸收;而层云的衰减虽然没有积云大，但是其使辐射衰减90%的距离也在60 m以内;相比而言，卷云对辐射的衰减很微弱，同样衰减的情况下，卷云的传输距离远大于另外两种的传输距离。计算结果对空中红外目标的探测具有一定的指导意义，可以为目标与背景的判别提供依据。

［1］ ZHANG Jianqi，FANG Xiaoping.Infrared Physics［M］.Xi’an:Xidian University Press，2007:182－182.(in Chinese)张建奇，方小平.红外物理［M］.西安:西安电子科技大学出版社，2007:182－182.

［2］ ZHOU Xiuji，et al.Advanced atmospheric physics［M］.Beingjing:China Meteorological Press，1991:814－815.(in Chinese)周秀骥，等.高等大气物理学［M］.北京:气象出版社，1991:814－815.

［3］ BU Lingbing，ZHU Yazong，et al.Development of probe of cloud droplet［J］.Infrared and Laser Engineering，2011，40(10):1923－1927.(in Chinese)卜令兵，朱亚宗，等.激光云粒子探测技术［J］.红外与激光工程，2011，40(10):1923－1927.

［4］ WANG Haihua，SUN Xianming，et al.Polarization of light scattering by ice－water mixed clouds in visible regions［J］，Laser ＆ Optoelectronics Progress 2011，48(070101):1－5.(in Chinese)王海华，孙贤明，等.偏振光在冰水混合云中的传输特性［J］.激光与光电子学进展，2011，48(070101):1－5.

［5］ LIU Jianbin，LI Hai.Calculation of light scattering on water cloud particles by using Mie’s theory［J］.Journal of Guangxi University:Nat Sci Ed，2009，34(6):863－867.(in Chinese)刘建斌，李海.基于Mie理论的四种典型水云的光散射计算［J］.广西大学学报:自然科学版，2009，34(6):863－867.

［6］ LEI Bi，PING Yang，et al.Scattering and absorption of light by ice particles:Solution by a new physical－geometric optics hybrid method［J］.Journal of Quantitative Spectroscopy ＆ Radiative Transfer，2011，112:1492－1508.

［7］ SUN Xianming，SHEN Jin，et al.Error analysis of equivalent spheres model for computing the reflection properties of Ice clouds［J］.Acta Optica Sinica，2009，29(11):2963－2967.(in Chinese)孙贤明，申晋，等.等效球模型模拟冰晶云反射的误差分析［J］.光学学报，2009，29(11):2963－2967.

［8］ GONG Chunwen，WEI Heli，et al.Theinfluence of the aspect ratio to the light scattering properties of cylinder ice particles［J］.Acta Optica Sinica，2009，29(5):1155－1159.(in Chinese)宫纯文，魏合理，等.取向比对圆柱状冰晶粒子光散射特性的影响［J］.光学学报，2009，29(5):1155－1159.

［9］ XUE Lifang，WEI Heli，et al.Single－scattering properties of cirrus clouds in infrared region［J］.Laser ＆ Infrared，2004，34(4):286－291.(in Chinese)薛力芳，魏合理，等.卷云在红外波段的散射特性［J］.激光与红外，2004，34(4):286－291.

［10］ Robert Siegel，John R Howell.Thermal radiation heat transfer(third edition)［M］.Washington，DC:Hemisphere Publishing Corporation，1992:528－534.

［11］ PAN Hao.Calculation and image simulation of infrared radiation of cloud background［D］.Xi'an:Xidian University，2006:6－9.(in Chinese)潘皓.云背景红外辐射计算及图像仿真［D］.西安:西安电子科技大学，2006:6－9.

［12］ YUAN Yijun，REN Deming，et al.Computing scattering phase function by recursive formula of mie theory［J］.Chinese Journal of Light Scattering，2006，17(4):366－371.(in Chinese)袁易君，任德明，等.Mie理论递推公式计算散射相位函数［J］.光散射学报，2006，17(4):366－371.

［13］ XIANG Jiansheng，HE Junhua.Numerical calculation of Mie theory［J］.Journal of applied optics，2007，28(3):363－366.(in Chinese)项建胜，何俊华.Mie光散射理论的数值计算方法［J］.应用光学，2007，28(3):363－366.