高精度干涉测高雷达回波快速实现方法
宋兵兵,潘明海,梁志恒,朱学玲
(1.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京210016;2.清华大学精密仪器系,北京100084)
回波模拟半实物仿真是研究雷达系统参数及其处理算法的有效手段,尤其是在实际雷达系统尚未建立,缺乏真实的回波数据,回波模拟仿真便成为系统分析和成像算法验证的唯一工具[1-2]。
合成孔径雷达(synthetic aperture radar,SAR)回波仿真算法可以分为时域算法[3-4]、二维频域算法[5-6]和逆成像回波算法[7-9]。时域算法能真实反映回波生成,可移植性较强,易于引入运动误差模型,算法的精度比后两种好,缺点是计算复杂度高。二维频域算法在二维频域内采用二维快速傅里叶变换FFT代替时域卷积,大大提高了回波生成的速度,但由于采用了频域插值和驻定相位近似,降低了回波信号的相位仿真精度,且运动误差模型的引入较为困难。逆成像回波算法也具有快速计算的功能,但是算法相位精度较低且难以引入实际的误差模型,并且局限性比较强[9]。以往对回波的高精度模拟研究大多是从理论公式出发,计算繁琐,不利于回波数据的快速生成;并且在模拟器的设计过程中,往往需要与实际雷达发射源对接,需要按照实际的带有信号畸变的发射信号对目标回波进行模拟,只能对采样后数字化的发射信号进行卷积操作,无法得到回波的解析表达式,在工程实现上有一定的局限性;而常用的适用于工程实现的方法大多采用雷达发射信号与场景调制信息直接卷积的方式,仿真精度受限于采样频率,不能很好地满足高精度测试的要求[10-12]。
本文针对时域相干模拟法进行改进,从信号系统角度出发,将回波信号看作是雷达发射信号通过地面反射系统的零状态响应,无需雷达发射信号表达式,只需将采样得到的雷达发射信号与系统冲激响应相卷积,即可得到回波信号。并在原有方法基础上对处理过程中的数据进行升采样,尽可能减小因距离取整带来的相位误差,处理完成后再进行抽取恢复到原始的采样率,便于工程上实现。同时采用GPU完成回波数据的快速产生,极大地提高了运算效率,缩短了回波数据产生所需的时间。
1 系统原理
干涉测高雷达的测量目标一般是山地、丘陵、平原等大场景,因此其回波信号仿真技术可以以SAR信号仿真技术为基础,对回波信号仿真技术的研究主要集中在SAR回波仿真。普通的SAR系统只是利用雷达复图像的幅度信息,而干涉测高雷达系统则利用干涉技术,通过相位差信息得到观测区域的高程。
对于干涉测高雷达而言,其单个接收通道的几何配置关系与SAR的几何配置是一致的[13]。
假设在某一个时刻tn,雷达发射的线性调频信号的表达式可以写为
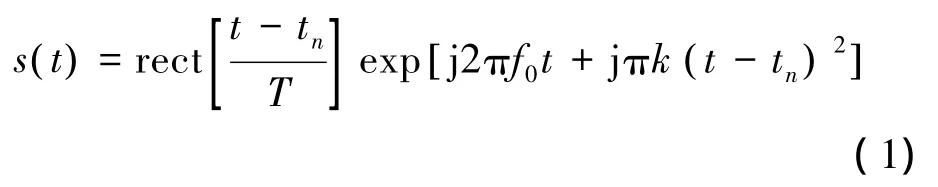
该线性调频信号被地面的点目标P反射之后雷达接收到的信号经过解调之后去除载频项得到点目标的SAR回波计算公式为
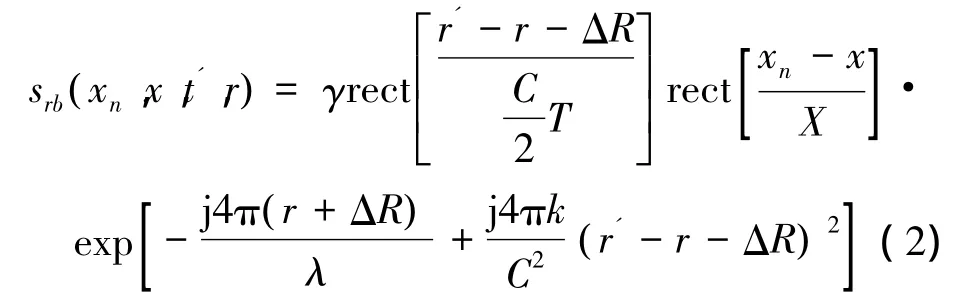
式中:γ代表点目标P的反射率,C代表光速,X代表合成孔径长度,R为P点和平台所在的位置之间的距离,t'=t-tn,ΔR= ( xn-x )2/2/r,r'=Ct'/2相当于是距离向采样空间间隔。
地面照射带由许多点目标构成,这些点目标的SAR回波的叠加即为整个成像的SAR回波:


干涉测高雷达回波信号产生的第一步是计算系统冲激响应。先计算每个散射点的距离,根据距离可以确定回波相位以及该散射点所处的距离门,最后对处于同一个距离门的目标信息进行累加得到冲激响应。
在实际的模拟信号域中,回波信号的位置是连续的,然而在实际卷积过程中,由于进行了数字离散化操作,各散射点回波的起始位置离散到各个距离门之后变成了离散化的整数值,也就是说,回波信号的起始点是离散的,这将导致回波处理的相位产生较大的误差。例如对Dechirp的信号处理过程,回波信号的起始位置决定着Dechirp处理之后信号的基准频率。在实际的模拟信号域中,回波信号的位置是连续的,因此各散射点回波信号Dechirp之后的基准频率也是连续变化的。然而在实际卷积过程中,由于进行了数字离散化的操作,各散射点的回波起始位置离散到各个距离门之后变成了离散化的整数值。在计算过程中往往只能保证雷达与散射点距离造成的波程相位与实际相位相同,却难以保证散射点的冲激响应与发射信号卷积后再进行Dechirp处理后其回波基准频率与实际情况一致,经过一段时间的信号积累,实际相位差别将越来越大。
以B=200 MHz带宽、τ=5 μs脉宽的线性调频信号为例,如果采用fs=300 MHz采样率的信号对其进行采样,那么每一个采样的距离门时间间隔将为1/fs=3.333 ns,而该信号的线性调频率为k=B/τ=4×1013Hz/s,即对应一个离散化的距离门,频差将达到133 kHz,如果采用舍去小数点取整的方式,造成的频差最大可达133 kHz,虽然初始的相位与实际相位一致,但在5 μs的信号持续时间内,回波信号频率不准确,其相位与实际情形最大差可达240°,即在此条件下卷积的离散化数字处理造成的回波信号相位量化误差最大可达240°,而系统辨识误差一般只有十几度,远不能满足仿真要求。
为了使得回波信号与实际情况一致,消除离散化的误差,需要对离散化过程中舍去的距离进行补偿,即对卷积后的信号进行非整数倍的位移,在文献[14]中给出了具体的实现方法如下:在傅里叶变换中存在如下性质:若f( t)的傅里叶变换为F( ω),则f( t -t0)的傅里叶变换为F( ω)e-jωt0,因此在时域中目标位置的平移可以等价为回波多普勒域中相位的偏移,用类似的方法可以在原始回波的多普勒域中实现非整数倍采样间隔的平移。在时域中要平移dt个采样间隔,相当于在离散化的多普勒域中整体相移dt·ω,此时信号的非整数倍采样间隔位移在多普勒域中已经完成。
需要注意的是,该方法虽然能精细补偿非整数倍的位移,但由于地面上每一个散射点到雷达的距离不同,离散化后每个点舍去的距离也不相同,因此,需要补偿的非整数倍位移也不相同,即需要对地面上的点进行逐点补偿操作,计算量非常庞大。
一般来说,卷积的离散化数字处理造成的回波信号相位量化误差不超过系统可辨识误差的1/10时,就能满足仿真要求,可以不对信号进行位移补偿。基于此,可通过提高系统采样率的方法来减小离散化数字处理造成的回波相位量化误差。假设在设定条件下离散化数字处理造成的回波信号相位量化误差最大为240°,将采样率提升至原先的200倍,则最大频差将会变为原先的1/200(665 Hz),而离散化数字处理造成的回波相位量化误差最大只有1.2°,小于系统辨识误差的1/10,满足要求。
2 系统仿真流程
回波模拟是干涉测高雷达系统仿真中的重要组成部分,回波模拟的计算性能,直接影响整个仿真的性能,采用GPU计算回波,可以获得良好的性能提升。
回波模拟的任务是接收雷达射频发射信号或中频发射信号,为雷达提供射频目标回波信号或中频目标回波信号。为了适应雷达双通道干涉测高体制,需要产生两通道相参射频信号,因此,基带回波产生单元和上变频单元都为相同的2个通道。系统框图如图1所示。

图1 干涉测高雷达目标回波模拟器系统框图Fig.1 System block diagram of the echo simulator
回波模拟最关键的步骤是系统冲激响应的计算。系统冲激响应计算在实验前完成,需要根据地面、海面场景,飞行位置、速度、姿态,雷达波束指向,计算波束照射区中每个散射点到两个接收端的幅度、相位、延迟,散射点距离门矢量叠加,形成系统冲激响应。具体流程如图2所示。
完成系统冲激响应的计算后,利用冲激响应与采集的雷达发射信号卷积,即可得到基带回波信号。完整的回波产生流程如图3所示。

图2 系统冲激响应计算流程图Fig.2 Calculation flowchart of system impulse response

图3 干涉测高雷达目标回波模拟器工作流程Fig.3 Workflow of the echo simulator
3 仿真结果分析
3.1 计算量分析
对于模拟器的回波仿真,在不知道回波数学表达式的前提下,要按照系统要求的精度进行仿真,仿真步骤如下:
1)计算当前散射点与雷达的距离,从而得到该点的延迟相位、落入的距离门编号以及需要补偿的非整数倍位移;
2)将该点的冲激响应与发射信号的进行卷积;
3)对该点信号进行非整数倍的位移补偿;
4)将得到的有效信号叠加至输出的总的回波数组中。
以雷达飞行高度照射面积4.5 km×4.5 km,一次覆盖采样点900×900点来计算,一个PR需要计算81万个点的操作步骤,即81万次获取单点信号的冲激响应;81万次卷积(与信号长度相当的复乘操作);81万次非整数倍的位移补偿(每次都包括一次FFT,一次FFT长度的相移补偿数组构造,一次FFT长度的复乘运算,一次IFFT);叠加至总的回波数组包括一次FFT长度的附加运算。计算量非常庞大。
而利用改进的升采样计算方法计算步骤为:
1)在回波仿真初始化时,模拟器对雷达发射的基带信号进行采样,采样后将发射信号送入GPU;
2)GPU根据仿真精度需求,对送入的数字化发射波形进行插值,从而得到高采样率的基带信号;
3)逐点计算地面散射点的冲激响应,并将其叠加到对应的距离门中,从而获得地面散射点的整体冲激响应(注:该距离门是高采样率对应的距离门,地面散射点的冲激响应是高采样率的冲激响应);
4)对高采样率的冲激响应与高采样的发射信号进行卷积操作,得到高采样的回波信号;
5)对高采样的回波信号进行抽取处理,恢复成模拟器当初送入GPU的采样率的回波信号,并将其存入存储板。
以雷达飞行高度照射面积4.5 km×4.5 km,一次覆盖900×900个采样点来计算,假设采样率提高200倍,一个脉冲需要计算81×200万个点的冲激响应以及81×200万次的复加,再进行一次卷积,一次FFT,一次FFT长度的复乘,以及一次IFFT,输出是再有一次降采样输出,计算量大大降低。
3.2 计算效率比较
根据以上讨论的模型,分别利用CPU和GPU快速生成干涉测高雷达回波。CPU选用Intel i7处理器(8核,3.4GHz主频),GPU选用3块NVIDIA GTX680显卡,内存均为1 333 MHz,32 Gbytes。CPU选用的开发环境为Visual Studio 2010,GPU选用的开发环境为Nvidia Cuda 5.0。仿真实验的计算参数设置为:脉冲重复频率(PRF)为100 kHz;采样率为300 MHz;仿真区域大小为4.5 km×4.5 km;仿真分辨率为5 m×5 m,仿真时长为10 s。按照上述参数分别采用CPU和GPU进行仿真计算,CPU用时8 h,而GPU仅用时80 s。可以看出,采用GPU做干涉测高雷达回波快速计算,计算速度相对PC机提高360倍左右,有效解决了当前普遍存在的回波计算效率极低的问题。
3.3 雷达处理结果分析
利用本文所述方法和设备针对不同地形产生回波信号,并将模拟器与雷达对接,利用雷达对不同起伏地形的回波进行处理,并将处理结果导入MATLAB进行分析,获得的高程结果如图4所示。

图4 干涉测高雷达处理结果Fig.4 Processing result of interferometric radar
由测试结果可以看出,雷达测试结果在合理的范围内。本文的回波实现方法能够为雷达提供高精度的回波信号,能够真实的反映雷达的性能,很好地完成对雷达的验证工作。
4 结束语
本文分析了雷达回波半实物仿真与数字仿真的区别,根据半实物仿真无法准确得到回波数学表达式的特点,利用提高采样率的办法提高半实物仿真中回波相位模拟精度,将GPU平台引入回波模拟器实现回波的快速生成,大大提高了仿真系统的工作效率,初步解决了精度与计算效率的矛盾,为干涉测高雷达研制与测试提供了一个有效的工具。但是仿真方法采用的是回放模式,未能完全实现实时计算,有待于进一步的研究和优化。
[1]DURO J,ALBIOL D,KOUDOGBO F N,et al.Emulation of TOPSAR data from TerraSAR-X Stripmap mode[C]//Proc of EUSAR.Aachen,Germany,2010:1-4.
[2]QIU Xiaolan,HU Donghui,ZHOU Liangjiang,et al.A bistatic SAR raw data simulator based on inverse ω-k algorithm[J].IEEE Transactions on Geosciences and Remote Sensing,2010,48(3):1540-1547.
[3]KAUPP V H,WAITE W P,MACDONALD H C.SAR simulation[C]//Proceedings of IGARSS'86.Zurich,Switzerland,1986:1645-1650.
[4]MORI A,DE VITA F.A time-domain raw signal simulator for interferometric SAR[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(9):1811-1817.
[5]FRANCESCHETTI G,IODICE A,PERNA S,et al.SAR sensor trajectory deviations:Fourier domain formulation and extended scene simulation of raw signal[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(9): 2323-2334.
[6]FRANCESCHETTI G,IODICE A,PERNA S,et al.Efficient simulation of airborne SAR raw data of extended scenes[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(10):2851-2860.
[7]ELDHUSET K.High resolution spaceborne INSAR simulation with extended scenes[J].IEEE Proceedings of Radar Sonar Navigation,2005,152(2):53-57.
[8]LU Hao,CAN Ning,LIU Weiwei,et al.Efficient SAR raw data simulation of extended scenes using chirp scaling principle[C]//Proceedings of the 1st International Conference on Information Science and Engineering(ICISE).Nanjing,2009:554-557.
[9]汪丙南,张帆,向茂生.基于混合域的SAR回波快速算法[J].电子与信息学报,2011,33(3):690-695.
WANG Bingnan,ZHANG Fan,XIANG Maosheng.SAR raw signal fast algorithm in mixed domain[J].Journal of Electronics&Information Technology,2011,33(3):690-695.
[10]王虹现,全英汇,邢孟道,等.基于FPGA的SAR回波仿真快速实现方法[J].系统工程与电子技术,2010,32 (11):2284-2289.
WANG Hongxian,QUAN Yinghui,XING Mengdao,et al.Fast realization of SAR echo simulation based on FPGA[J].Systems Engineering and Electronics,2010,32 (11):2284-2289.
[11]汪丙南,陈立福,向茂生.基于起伏地形的干涉SAR回波数据仿真[J].宇航学报,2011,32(9):1986-1993.
WANG Bingnan,CHEN Lifu,XIANG Maosheng.SAR echo data simulation based on undulated terrain[J].Journal of Astronautics,2011,32(9):1986-1993.
[12]何志华.分布式卫星SAR半实物仿真关键技术研究[D].长沙:国防科学技术大学,2011:67-70.
HE Zhihua.Study on key techniques of distributed spaceborne SAR hardware-in-the-loop simulation[D].Changsha:National University of Defense Technology,2011:67-70.
[13]夏伟杰.合成孔径雷达回波仿真与图像模拟[D].南京:南京航空航天大学,2010:68-70.
XIA Weijie.Simulation of raw signal and image of synthetic aperture radar[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:68-70.
[14]袁昊,周荫清,李景文.任意沿轨基线长度双孔径SARATI动目标检测方法[J].系统工程与电子技术,2007,29(9):1413-1419.
YUAN Hao,ZHOU Yinqing,LI Jingwen.MTI method with the along-track baseline of any length based on dual-aperture SAR-ATI[J].Systems Engineering and Electronics,2007,29(9):1413-1419.

