薛定谔猫态光场与二能级原子相互作用系统的量子特性

李鹏茂, 萨楚尔夫,2, 苏少龙

(1.内蒙古师范大学物理与电子信息学院, 呼和浩特 010022； 2.内蒙古师范大学图书馆, 呼和浩特 010022)

薛定谔猫态光场与二能级原子相互作用系统的量子特性

李鹏茂1, 萨楚尔夫1,2, 苏少龙1

(1.内蒙古师范大学物理与电子信息学院, 呼和浩特 010022； 2.内蒙古师范大学图书馆, 呼和浩特 010022)

在非旋波近似下,通过采用相干态正交化展开的方法,研究了薛定谔猫态光场与二能级原子相互作用系统中,原子的布局数和光场的反聚束效应,并与旋波近似下的结果进行了对比.在旋波近似与非旋波近似下,讨论了初始光场强度、相干态间的相位角以及失谐量对原子布局数和光场反聚束效应的影响；在非旋波近似下,讨论了强弱耦合情况下光场的反聚束效应.研究结果表明：旋波近似与非旋波近似下,原子的布局数随着初始光场强度的不同,表现出不同的特性；当初始光场强度较小时,旋波近似与非旋波近似下,原子的布局数表现出相同的特性；随着初始光场强度的增大,旋波近似下,原子的布局数将表现出坍塌现象.耦合强度较大时,光场的聚束与反聚束效应在非旋波近似与旋波近似下有较大的区别；非旋波近似下,随着初始光场强度的增大,光场一直处于聚束效应状态；而旋波近似下,光场的聚束效应与反聚束效应交替出现.

薛定谔猫态; 非旋波近似; 布局数反转; 反聚束效应

1 引 言

近几十年来,量子光学的重要进展之一就是构造出了许多光场的非经典态,薛定谔猫态就是其中之一,它是由在宏观上可区分的两个或多个相干态叠加而形成的一种量子态,具有特殊的非经典特性.量子光学中,当原子与腔场的耦合强度较小时,旋波近似J-C模型因为可以精确求解而被广泛应用.人们利用这一模型对薛定谔猫态光场与原子相互作用系统的量子特性已进行了大量的研究,并取得了一系列重要的研究成果[1-6],如压缩性[5]、高阶压缩性、亚泊松分布以及光子数振荡等.随着技术的发展和研究水平的提高,近年来,人们开始利用量子固态装置代替传统的原子-腔模式,来研究原子与光场相互作用的量子特性.实验结果所提供的光谱分析表明,其耦合强度比原子-腔模式下获得的强度大3-4个数量级,此时系统中的光场压缩[6]、原子反转[7]、场Q函数、原子压缩等都与在旋波近似下所得的结果都有很大的不同.这是由于在非旋波近似下,相互作用系统中虚光子的作用引起的,所以研究非旋波近似J-C模型中的量子特性具有重要的理论和实际意义.本文将在非旋波近似下,通过采用相干态正交展开的方法,对薛定谔猫态光场与二能级原子相互作用系统中,原子的布局数反转和光场聚束效应进行了研究.

2 理论模型及求解

在非旋波近似下,一个单模光场与二能级原子相互作用哈密顿量为(ћ=1)

(1)

对(1)式做如下变换：

(2)

则(1)式可表示为：

(3)

现令(3)式的定态波函数为

|-〉=|φ1〉|e〉+|φ2〉|g〉

(4)

将(3)和(4)式代入薛定谔方程：

H|-〉=E|-〉,

(5)

利用|e〉,|g〉的正交性得：

(6)

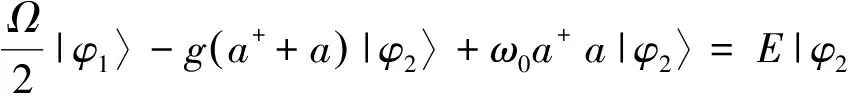
(7)

引入新的玻色算符[7-8]

则(6)和(7)式可以改写为

(8)

(9)

令

(10)

其中|n〉A,|n〉B分别为A空间或B空间的Fock态,或称为平移Fock态[9](displacedFockstate).所以由|n〉A和|n〉B构成了两组新的完备归一基.|n〉A和|n〉B的定义如下：

(11)

(12)

(13)

(14)

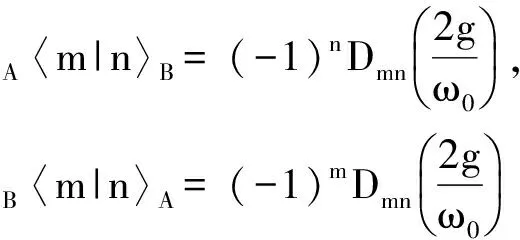
(15)

(16)

假设腔场的初态处于薛定谔猫态

(17)

式中：

若原子初始时刻处于上能级,则

|t=0〉=|α,φ〉|E〉

(18)

将(2)和(17)式代入(18)式并根据|e〉,|g〉的正交性,(18)式可转变为

(19)

(20)

对(19)和(20)两式分别左乘A〈m|,B〈m|,得

(21)

(22)

(23)

对(21)和(22)式求解,可求出fi,则任意时刻的波函数可表示为

(24)

3 数据处理及结论分析

由于布局数反转W(t)以及二阶相干度G2(t)的表示形式十分复杂,对于布局数反转W(t)和二阶相干度G2(t)与各参量的相互影响关系将采用数值计算的方法进行分析.下面主要分析和讨论相干态间的相位角、初始光场强度和耦合强度对原子布局数反转W(t)和光场的二阶相干度G2(t)的影响.

3.1 原子的布局数反转

由(24)式可以得到原子处于上能级的布局几率为：

所以原子的布局数反转相应为

W(t)=2P上-1

3.2 光场的反聚束效应

光场的聚束与反聚束效应由二阶相干度来描述,二阶相干度定义为

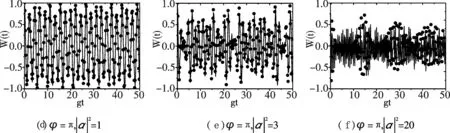
图取不同值时原子布局数反转的时间演化曲线Fig.1 The time evolution of atomic population for different |α|2

其中

若G2(t)>1,则光场表现为聚束效应,G2(t)<1则为反聚束效应,当G2(t)=1时,则光场表现为聚束与反聚束的一个临界状态.

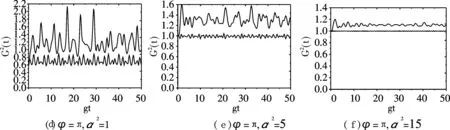
图取不同值时二阶相干度G2(t)的演化Fig.2 The time evolution of the degree of second order coherence for different |α|2

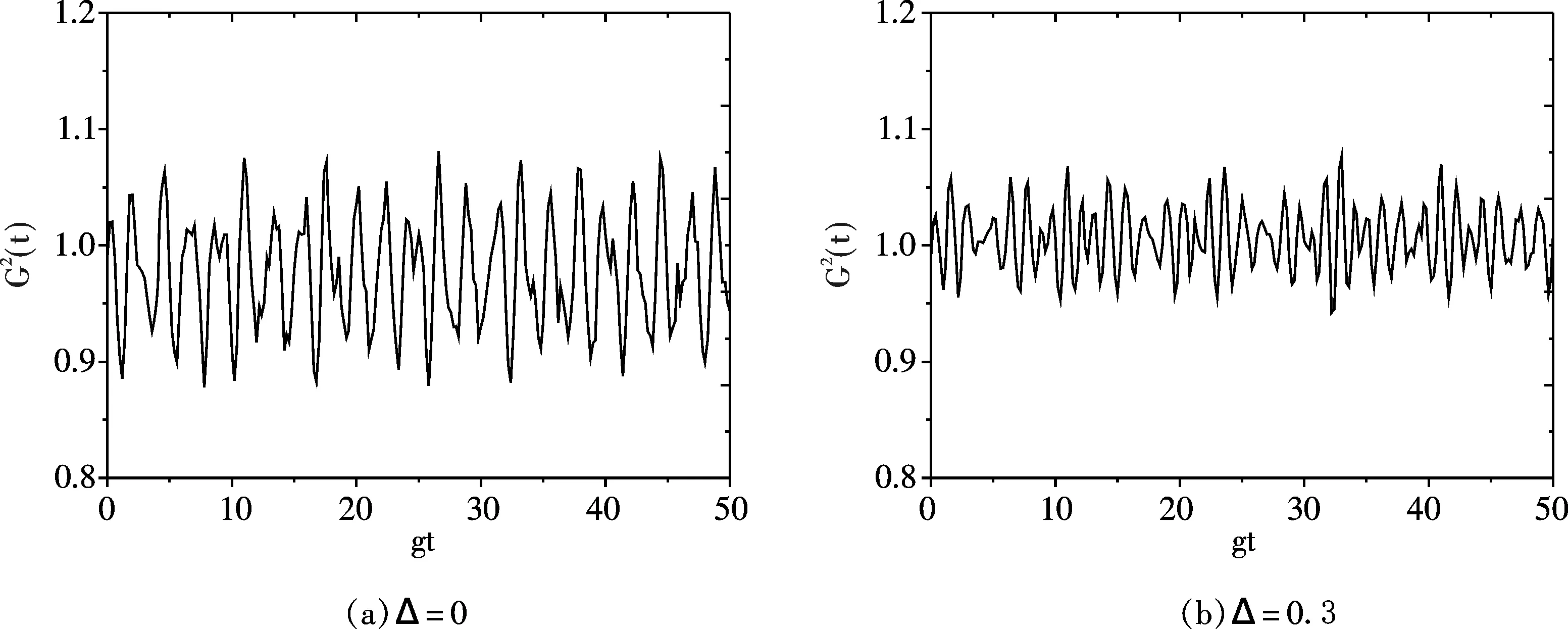
图 3 非旋波近似下,失谐量Δ取不同值时二阶相干度G2(t)的演化Fig.3 The time evolution of the degree of second order coherence for different detuning volumes without RWA

4 结 论

本文通过采用相干态正交展开的方法,在非旋波近似J-C模型下,对薛定谔猫态光场与二能级原子相互作用的量子特性进行了研究,并与旋波近似下的结果进行了对比.结果表明,随着初始光场强度的增大,在非旋波近似下,原子的布局数不会出现完全塌缩现象,而是出现很多锯齿状的高频振荡,但是在旋波近似下,原子的布局数会出现完全塌缩现象；对于光场的反聚束效应,在非旋波近似下,光场完全表现出聚束效应,而旋波近似下光场的聚束与反聚束效应交替出现.产生这些现象的原因在于非旋波项的存在,并且在光场强度比较大时,非旋波项对系统量子特性的影响也比较大.

[1]RenXZ,JiangDL,CongHL.Exactcalculationsoftheenergyspectraandthedynamicalpropertiesofatwo-levelsystem[J].ActaPhysicaSinica, 2009, 58 (8): 5394(in Chinese)[任学藻, 姜道来, 丛红璐. 精确计算非旋波近似下二能级系统的能谱和动力学性质[J]. 物理学报, 2009, 58(8): 5394]

[2] Liu S Q, Guo Q, Tao X Y. Quantum dynamics of a cascade three-level atom interacting with coherent state in the counter rotating wave approximation[J].ActaPhysicaSinica, 1998, 47(9): 1481(in Chinese)[刘三秋, 郭琴, 陶向阳. 非旋波近似下级联型三能级原子与腔场相互作用的量子动力学性质[J]. 物理学报, 1998, 47(9)： 1481]

[3] Liu T, Wang K L, Feng M. Lower ground state due to counter-rotating wave interaction in a trapped ion system [J].Phys. B, 2007, 40: 1967.

[4] Liu T, Feng M, Wang K L. Exact solution of quantum dynamics of a cantilever coupling to a single trapped ultracold ion [J].CommonTheor.Phys., 2007, 47 (3): 561.

[5] Peng J S, Li G X. Influences of the virtual photon process on the squeezing effects of a single mode light field [J].ActaPhysicaSinica, 1993, 42(4): 568(in Chinese)[彭金生, 李高翔. 虚光子过程对光场压缩的影响[J]. 物理学报, 1993, 42(4)：568]

[6] Wu S M, Sachuerfu, Bao L. The atomic population inversion in the system of Schrödinger cat state light field interacting with a two-level Atom under intrinsic decoherence condition [J].J.InnerMongoliaNormalUniv.:Nat.Sci.Ed., 2010, 39 (1): 40(in Chinese)[吴淑梅, 萨楚尔夫, 包丽. 存在内禀退相干时薛定谔猫态光场中原子的布居数反转[J]. 内蒙古师范大学学报(自然科学汉文版), 2010, 39(1)： 40]

[7] Chen Q H, Zhang Y Y, Liu T,etal. Numerically exact solution to the finite-size Dicke model [J] .Phys.Rev. A, 2008, 78 (5): 051801.

[8] Irish E K, Gea-Banacloche J, Martin I,etal. Dynamics of a two-level system strongly coupled to a high-frequency quantum oscillator [J].Phys.Rev. B, 2006, 72： 195410.

[9] Yurke B, Stoler D. Generating quantum mechanical super positions of macroscopically distinguishable states via amplitude dispersion [J].Phys.Rev.Lett., 1986, 57(1): 13.

[10] Zhang C H, Sachuerfu, Ge R L. Evolution of field entropy in a system of Schrödinger cat state light field interacting with two moving entangled atoms [J].J.At.Mol.Phys., 2008, 25(6): 1415(in Chinese)[张彩花, 萨楚尔夫, 格日乐. 运动纠缠双原子与薛定谔猫态光场相互作用系统的场熵演化[J]. 原子与分子物理学报, 2008, 25(6)： 1415]

[11] Wang X C, Cao Z L. Photon antibunching effect in the system of two-mode entangled coherent states interacting with a moving V-type three-level atom [J].J.At.Mol.Phys., 2007, 24 (4): 785(in Chinese)[汪贤才, 曹卓良. 双模光场与运动三能级原子作用系统的反聚束效应[J]. 原子与分子物理学报, 2007, 24(4): 785]

[12] Franco R Lo, Compagno G, Messina A,etal. Single-shot generation and detection of a two-photon generalized binomial state in a cavity [J].Phys.Rev. A, 2006, 74: 045803.

[13] Cirac J I, Zoller P. Quantum computations with cold trapped ions [J].Phys.Rev.Lett., 1995, 74: 4091.

[14] Zheng S, Zhu X W, Feng M. Motional quantum-state engineering and measurement in the strong-excitation regime [J].Phys.Rev. A, 2000, 62: 033807.

[15] Milburn G J. Intrisic decoherece in quantum mechanics [J].Phys.Rev. A, 1991, 44: 5401.

Quantum properties in a system of interaction between a two-level atom and the Schrödinger cat state

LI Peng-Mao1, Sachuerfu1, 2, SU Shao-Long1

(1.College of Physics and Electronic Information, Inner Mongolia Normal University, Hohhot 010022, China；2. Library of Inner Mongolia Normal University, Huhhot 010022, China)

Applying the method of coherent states orthogonalization expansion, the atomic population and the antibunching effect of the light field are studied in the system of interaction between a two-level atom and the Schrödinger cat state without rotating wave approximation (RWA). The results are compared with those in RWA. The influences of the original strength of the light field and two coherent phase angles on the atomic population and antibunching effect with RWA and without RWA are discussed respectively, and the antibunching effect in the weak coupling condition is also discussed without RWA. The results show that the atomic populations with RWA and without RWA have different properties with the different original strengths of the light field. As the original strength of the light field is smaller, the atomic populations with RWA and without RWA show the same properties, but with the increase of the original strength of the light field the population with RWA will show the collapse phenomenon. When the coupling strength is larger, the antibunching effects with RWA and without RWA have bigger difference. Without RWA the light field will appear bunching effect, whereas with RWA it will appear alternately the bunching effect and the antibunching effect with the increase of the original strength of light field.

Schrödinger cat state； Without RWA; Atomic population； The antibunching effect

103969/j.issn.1000-0364.2015.02.017

2013-11-06

内蒙古自然科学基金(2013MS0115)；内蒙古师范大学“十百千”人才项目(RCPY-2-2012-K-038)

李鹏茂(1988—),男,山西省临汾人,内蒙古师范大学硕士研究生,主要从事量子光学研究.

萨楚尔夫. E-mail: Sacrf@imnu.edu.cn

O431.2

A

1000-0364(2015)02-0275-06