利用超短的紫外光源来增强阿秒脉冲的强度
冯立强,刘 航
(1.辽宁工业大学理学院,锦州 121001; 2. 中国科学院大连化学物理研究所分子反应动力学国家重点实验室, 大连 116023;3.辽宁工业大学化学与环境工程学院,锦州 121001)
利用超短的紫外光源来增强阿秒脉冲的强度
冯立强1,2,刘 航3
(1.辽宁工业大学理学院,锦州 121001; 2. 中国科学院大连化学物理研究所分子反应动力学国家重点实验室, 大连 116023;3.辽宁工业大学化学与环境工程学院,锦州 121001)
本文理论提出了一种利用超短紫外光源来增强阿秒脉冲强度的方法. 计算结果表明, 当适当的加入一束62 nm或者125 nm超短紫外光源到双色激光场时, 不仅高次谐波的截止能量被延伸了, 而且谐波的强度也比原双色场时有明显的增强. 尤其是当采用125 nm光源时,谐波的强度被增强了2个数量级,并且形成了一个232 eV的超长平台区. 最后通过叠加谐波次数从113次到170次可获得脉宽仅为43 as的孤立阿秒脉冲, 其强度比原双色场情况下产生的阿秒脉冲增强了2个数量级.
高次谐波; 阿秒脉冲; 紫外光源
1 引 言
高次谐波(HHG)作为产生阿秒脉冲的最有效方法之一已经被广泛的研究并取得了很大的进展[1-3]. 高次谐波的辐射过程可以用Corkum提出的经典三步模型来理解[4]: 首先, 原子或者分子中的电子在库仑场和激光场的共同作用下穿透势垒离开原子实,即发生隧穿电离成为自由电子; 其次, 离开原子实的自由电子在受到远大于原子实库仑场的外激光场作用下运动, 获得能量; 最后, 当激光电场改变方向时, 它又回到原子实附近, 以一定的几率与母核发生回碰, 同时发射出谐波光子. 这个谐波产生过程在多光周期的飞秒激光脉冲驱动下每0.5个光周期都会重复1次, 直接选取高次谐波谱上的一段就会得到间隔为0.5个光周期的阿秒脉冲串. 然而, 在对电子动力学进行实时探测的过程中, 单个阿秒脉冲比脉冲串更具有实际应用价值, 因此, 在如何得到孤立的阿秒脉冲吸引了很多研究学者的目光. 目前主要有三种有效的方法来获得孤立的阿秒脉冲, 1) 利用少周期激光驱动场与物质相互作用[5]. 例如: E. Goulielmakis等人利用3.3 fs的近红外超短激光脉冲, 获得了 80 as的孤立阿秒脉冲[6]. 2) 利用高次谐波对驱动光场偏振性的敏感依赖特性, 通过调制两束泵浦光场的偏振特性来形成限制高次谐波产生的控制门[7]. 例如:Sansone等人用5 fs的激光脉冲, 经过啁啾补偿技术得到了单个130 as的脉冲输出[8]. 3) 利用双色或多色场控制方案[9-11]. 例如: Zeng等人利用6 fs/800 nm和21.3 fs/400 nm的组合激光场获得了65 as的孤立脉冲[12], 等.
但是, 应用上述方法获得的大部分阿秒脉冲的强度不够高, 以至于其应用受到了一定的限制. 所以如何增强阿秒脉冲的强度得到了人们广泛的关注. 最近Ishikawa[13]理论提出了当采用He+离子为模型时, 适当的加入一束高频控制场到原有激光场上, 高次谐波的辐射强度与单色场的相比最高能提高17个数量级. 利用这一方案, Li[14]等人利用5 fs/800 nm的啁啾场以及其27th谐波场组合而成的激光场获得了26 as的超短脉冲, 其强度比单色场时增强了7个数量级. Du[15]等人利用双色场以及一束高频控制场的组合场获得了24 as的孤立脉冲, 其强度比单色场事提高了3-4个数量级. 但是, 上述情况下所应用的脉冲的强度都太强 (1015-1016W/cm2) 或者脉冲宽度都太短 (5 fs), 这在国际上大多数实验室是很难获得的, 并且实验上要想获得密度较大的He+离子也是一件非常困难的工作.
因此, 鉴于上述原因, 本文采用双色红外场与一高频紫外场的组合场来增强谐波强度, 但是我们采用的双色场是大多实验室都可具备的, 即5 fs/800 nm, I1=8.0×1014W/cm2基频场和20 fs/2000 nm, I2=1.0×1014W/cm2控制场,并且我们采用的模型是中性原子He, 这在实验室中是非常容易获得的.若无特殊说明,本文均采用原子单位.
2 理论方法
本文中, 高次谐波以及阿秒脉冲可以通过数值求解含时薛定谔方程来得到[16], 在长度规范和电偶极近似下, 原子和强激光场相互作用的含时薛定谔方程为
φ(r,t),
(1)
其中V(r)=-1.535/r是氦原子的软核库伦势,φ(r,t)为电子波函数. 组合激光场可以表示为
E(t)=E1f1(t)cos(ω1t)+E2f2(t)cos(ω2t)
+E3f3(t-τdelay)cos(ω3(t-τdelay)),
(2)
其中Ei和ωi(i=1-3)分别为5 fs/800 nm, 20 fs/2000 nm激光场和超短紫外光源的振幅和频率. τdelay是超短紫外光源与800 nm激光场的延迟时间.脉冲的包络形状为高斯型, 即

(3)
其中τi(i=1-3)分别为两束激光场的半高宽度.
根据艾伦费斯特定律[17], 可以求得偶极加速度为
(4)
然后对其进行傅立叶变换便可以得到相应的高次谐波谱

(5)
最后, 通过适当的叠加谐波可以获得阿秒脉冲
(6)
3 结果与分析
图1(a)给出了He原子在双色激光场 (黑实线) 和双色激光场与超短远紫外场形成的组合场 (虚线,以下称为组合场) 下产生的谐波发射功率谱. 双色激光场为5fs/800nm,I1=8.0×1014W/cm2和20fs/2000nm,I2=1.0×1014W/cm2,超短远紫外场为1.0fs/62nm(1.0/125nm),I3=5.0×1013W/cm2. 从图中我们可以看到,对于双色激光场的情况, 谐波光谱形成了一个双平台的结构, 并且在第二节平台 (从第113次到263次) 上谐波的干涉结构非常的小,进而形成了一个232eV的超长平滑连续区. 但是, 我们发现谐波平台的强度不是很强,这不利于产生强度较高的阿秒脉冲. 但是, 当适当的加入超短紫外光源后 (对于62nm光源我们取ω1τdelay=2.0π, 对于125nm光源我们取ω1τdelay=1.2π, 这是我们发现的对谐波强度增强的最佳延迟时间), 谐波的强度比原双色场时分别增强了1 (相对于62nm, 红虚线) 和2个数量级 (蓝虚线). 但是, 我们发现对于加入62nm光源的情况, 虽然谐波的强度得到了增强, 但是谐波平台处的干涉也被增大了,这是不利于产生孤立阿秒脉冲的. 因此, 加入125nm,ω1τdelay=1.2π光源是最佳的组合场条件.

图1 (a) He原子在双色场 (黑实线) 和双色场与62 nm (红虚线) 以及125 nm (蓝虚线) 光源的组合场下的高次谐波图. (b) He原子在双色场和双色场与62 nm以及125 nm光源的组合场下的电离几率. 若无其它说明, 时间的单位都是800 nm激光场的周期Fig. 1 (a) HHG spectra for the two-color field (solid black line), the two-color field+62 nm pulse at ω1τdelay=2.0π (dash red line), and the two-color field+125 nm pulse at ω1τdelay=1.2π (dot blue line). (b) Ionization probabilities of the above three cases (Time is in unit of optical cycle of 800 nm pulse in all the following figures unless stated otherwise)
根据三步模型我们知道谐波的强度和电离几率是密切相关的. 所以为了更好的理解图1(a)中的谐波增强的机理, 我们计算了上述2种情况下的电离几率, 如图1(b)所示. 计算结果表明, 当加入62nm和125nm光源时电离几率与原双色场比较被明显的增强了, 进而导致了较大的谐波增强. 实际上, 应用62nm和125nm光源作为控制场是因为其光子的能量(E62nm=20.0eV和E125nm=9.92eV)近似等于He原子1s和2s态单双光子共振跃迁的能量[18]. 因此适当的加入62nm和125nm光源后,电子很容易被激发到2s激发态附近, 而由于激发态的电离能小于基态, 所以电子更容易电离, 进而增大了电离几率, 最终导致了谐波强度的增强.
下面为了更好的了解谐波发射的特点, 我们利用小波变换的方法[19]对上述情况做了进一步分析,如图2(a)-(c)所示. 从图中我们可以看出, 对于本章的这种脉冲激光场会产生三个主要的峰A1,A2,A3, 并且每个峰对应峰值中心左右都有两个“分支”, 被称为短量子路径 (左分支, 先回碰后电离)和长量子路径 (右分支, 先电离后回碰)[20]. 对于双色场的情况 (图2(a)), 峰A1和A3的长短量子路径的贡献几乎一样. 但是对于最高峰A2其短量子路径的贡献要大于长量子路径的贡献, 这也是谐波光谱平台区较光滑的原因. 对于加入62nm,ω1τdelay=2.0π的组合场情况 (图2(b)), 我们发现长短量子路径对于所有能量峰的贡献几乎一样, 因此导致了谐波谱上干涉增强. 但是对于加入125nm,ω1τdelay=1.2π的组合场情况 (图2(c)), 我们发现短量子路径的贡献要大于长量子路径, 也就是说短量子路径被选择出来对谐波发射起主要作用. 我们知道由于两个量子路径对于谐波发射的时间不同, 当叠加谐波时就会在一个周期里面出现2个分离的脉冲. 所以选择单一的量子路径是产生孤立阿秒脉冲的有效方法. 因此根据上面的分析, 我们适当的选取最佳组合场的113次到170次谐波进行叠加, 结果获得了一个43as的孤立阿秒脉冲, 如图3所示, 其强度比原双色场情况下产生的阿秒脉冲 (图3插图所示) 增强了2个数量级.
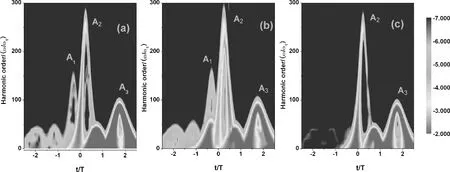
图2 (a)-(c) 双色激光场和上述组合场产生高次谐波的时频分析图Fig. 2 (a)-(c) The time-frequency harmonic distributions for the two-color field and the above two combined fields, respectively
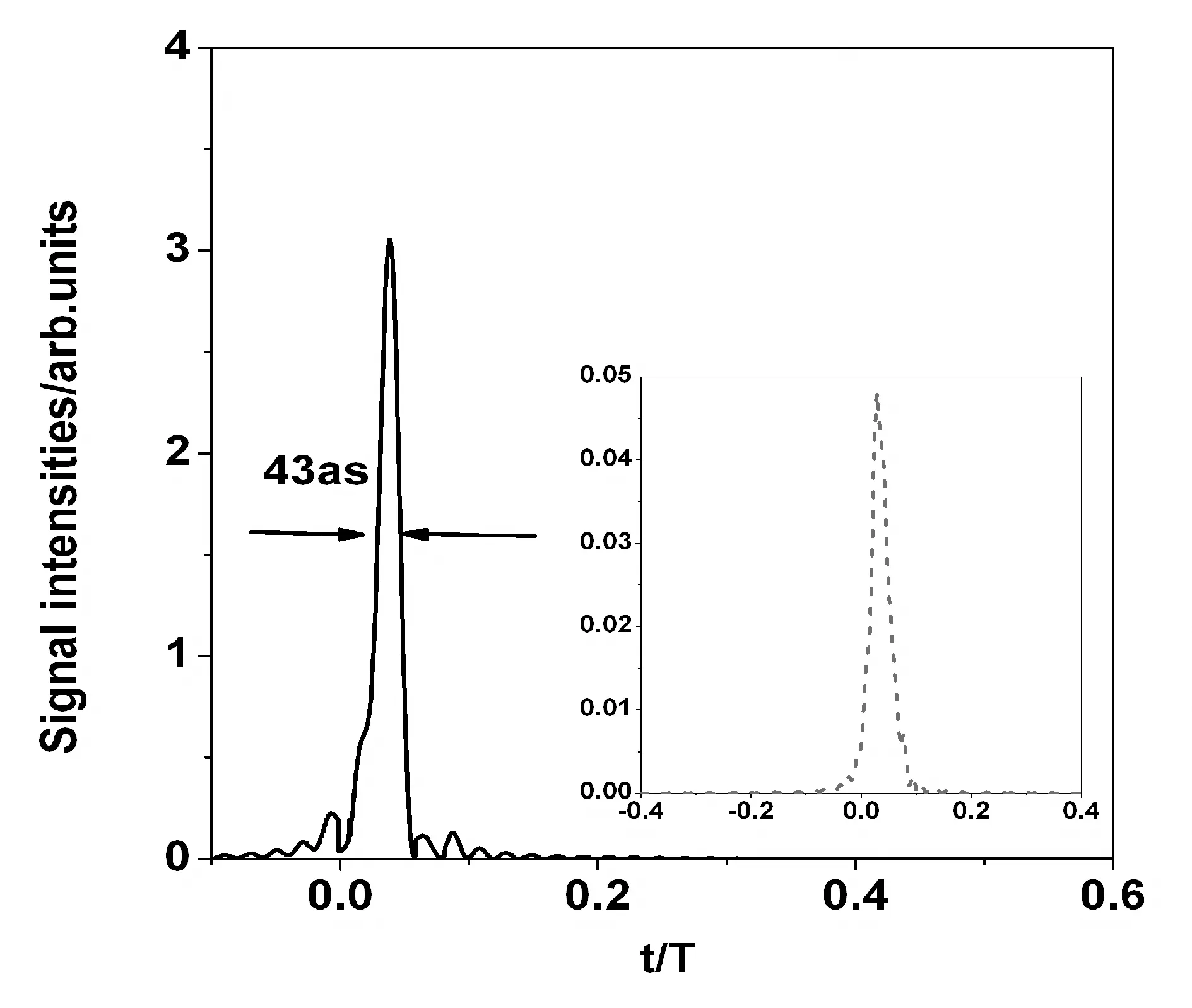
图3 叠加最佳组合场113次到170次谐波所产生的阿秒脉冲的时域包络曲线. 图3中插图给出的是原双色场下产生的阿秒脉冲Fig. 3 The temporal profile of the attosecond pulse by superposing the harmonics of the optimal combined field from the 113rd to the 170th order. The inset of Fig. 3 shows the attosecond pulse generated from the original two-color field
4 结 论
综上所述, 本文数值研究了超短紫外光源对谐波强度以及阿秒脉冲强度的影响. 计算结果表明,在He原子模型下, 适当的加入62nm或者125nm光源到双色激光场时, 谐波的强度被明显的增强了1个或者2个数量级. 尤其是当采用125nm光源场时, 谐波谱形成了一个232eV的超长平台区, 并且这一连续区几乎只由短量子路径贡献产生. 最后通过直接叠加最佳组合场谐波次数从113次到170次可获得脉宽仅为43as的孤立阿秒脉冲, 并且其强度比原双色场情况下产生的阿秒脉冲增强了2个数量级.
[1]MiaoXY,DuHN.Theoreticalstudyofhigh-order-harmonicgenerationfromasymmetricdiatomicmolecules[J].Phys.Rev. A, 2013, 87: 053404.
[2] Liu S S, Miao X Y. Enhancement of high-order harmonic emission by using a coherent superposition in a two-color laser field [J].J.At.Mol.Phys., 2012, 29(5): 881 (in Chinese) [刘莎莎, 苗向阳. 在双色场中使用相干叠加态来提高高次谐波的发射 [J]. 原子与分子物理学报, 2012, 29(5): 881]
[3] Du H N, Miao X Y. Theoretical exploration of intensity effects on high-order harmonic generation from H+2molecules [J].J.At.Mol.Phys., 2013, 30(1): 115 (in Chinese) [都慧妮, 苗向阳. 理论研究激光强度对H+2分子高次谐波产生的影响 [J]. 原子与分子物理学报, 2013, 30(1): 115]
[4] Corkum P B. Plasma perspective on strong field multiphoton ionization [J].Phys.Rev.Lett., 1993, 71: 1994.
[5] Feng L Q, Chu T S. High-order harmonic generation spectra and isolated attosecond pulse generation with a two-color time delayed pulse [J].J.Electron.Spectrosc.Relat.Phenom., 2012, 185: 39.
[6] Goulielmakis E, Schultze M, Hofstetter M,etal. Single-cycle nonlinear optics [J].Science, 2008, 320: 1614.
[7] Yao J P, Li Y, Cheng Y. Generation of isolated attosecond pulses with a specific waveform two-color laser field [J].Chin.Opt.Lett., 2011, 9: 041901.
[8] Sansone G, Benedetti E, Calegari F,etal. Isolated single-cycle attosecond pulses [J].Science, 2006, 314: 443.
[9] Feng L Q, Chu T S. High-order harmonics extension and isolated attosecond pulse generation in three-color field: Controlling factors [J].Phys.Lett. A, 2011, 375: 3641.
[10] Wu J, Zhang G T, Xia C L,etal. Control of the high-order harmonics cutoff and attosecond pulse generation through the combination of a chirped fundamental laser and a subharmonic laser field [J].Phys.Rev. A, 2010, 82: 013411.
[11] Feng L Q, Chu T S. Generation of an isolated sub-40-as pulse using two-color laser pulses: Combined chirp effects [J].Phys.Rev. A, 2011, 84: 053853.
[12] Zeng Z, Cheng Y, Song X,etal. Generation of an extreme ultraviolet supercontinuum in a two-color laser field[J].Phys.Rev.Lett., 2007, 98: 203901.
[13] Ishikawa K. Photoemission and ionization of He+under simultaneous irradiation of fundamental laser and high-order harmonic pulses [J].Phys.Rev.Lett., 2003, 91: 043002.
[14] Li P C, Zhou X X, Wang G L,etal. Isolated sub-30-as pulse generation of an He+ion by an intense few-cycle chirped laser and its high-order harmonic pulses [J].Phys.Rev. A, 2009, 80: 053825.
[15] Du H C, Wang H Q, Hu B T. Isolated short attosecond pulse generated using a two-color laser and a high-order pulse [J].Phys.Rev. A, 2010, 81: 063813.
[16] Lu R F, Zhang P Y, Han K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields [J].Phys.Rev. E, 2008, 77: 066701.
[17] Burnett K, Reed V C, Cooper J,etal. Calculation of the background emitted during high-harmonic generation [J].Phys.Rev. A, 1992, 45: 3347.
[18] Chen S H, Ruiz C, Becker A. Double ionization of helium by intense near-infrared and VUV laser pulses [J].Phys.Rev. A, 2010, 82: 033426.
[19] Antoine P, Piraux B, Maquet A. Time profile of harmonics generated by a single atom in a strong electromagnetic field [J].Phys.Rev. A, 1995, 51: R1750.
[20] Mairesse Y, Bohan A D, Frasinski L J,etal. Attosecond synchronization of high-harmonic soft x-rays[J].Science, 2003, 302: 1540.
Ultrashort ultraviolet source assisted enhancement of the attosecond pulse intensity
FENG Li-Qiang1, 2, LIU Hang3
(1.College of Science, Liaoning University of Technology, Jinzhou 121001, China; 2. State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics Chinese Academy of Sciences, Dalian 116023, China; 3.School of Chemical and Environmental Engineering, Liaoning University of Technology, Jinzhou 121001, China)
A promising method to improve the attosecond pulse intensity has been theoretically presented with the assisted of an ultrashort ultraviolet pulse. It shows that by properly adding an ultrashort 62 nm or 125 nm ultraviolet pulse to the synthesized two-color field, not only the harmonic cutoff but also the harmonic yield are remarkably enhanced compared with the original two-color field case. Especially for adding the 125 nm pulse case, the harmonic yield is enhanced by 2 orders of magnitude, and an ultrabroad 232 eV bandwidth is obtained. Finally, by superposing harmonics from the 113th to the 170th, an intense isolated pulse as short as 43 as can be directly produced, which is 2 orders of magnitude higher than the case of generation from the original two-color field.
High-order harmonic generation (HHG); Attosecond pulse; Ultraviolet source
2014-08-23
辽宁工业大学教师科研启动基金(X201312, X201319);辽宁省教育厅基金(L2014242)
冯立强(1985—),男, 辽宁沈阳人, 博士, 讲师. E-mail: lqfeng1101@126.com
103969/j.issn.1000-0364.2015.08.015
O562.4
A
1000-0364(2015)08-0616-05

