第一性原理对XMgn(X=K, Na, n=1-12)团簇结构与性质的研究

伏春平, 孙凌涛, 程正富

(重庆文理学院物理系, 重庆 402160)

第一性原理对XMgn(X=K, Na,n=1-12)团簇结构与性质的研究

伏春平, 孙凌涛, 程正富

(重庆文理学院物理系, 重庆 402160)

本文基于第一性原理的广义梯度近似GGA下对XMgn(X=K, Na,n=1-12)团簇的结构与性质进行了研究. 通过对结构、束缚能、二阶能量差分和劈裂能的分析发现: KMgn(n=1-12) 团簇在n>5时, 其几何结构转变为笼状; 在n=12时, K原子进入到团簇的内部且呈逃逸的趋势; KMgn(n=1-12)团簇的相对稳定性在n=6,9时增强; 对于NaMgn(n=1-12) 团簇, 在n<6时,团簇的结构相对简单; 在n大于等于6时,团簇的结构呈现出比较复杂的立体结构; NaMgn(n=1-12)团簇在n=6,9时团簇的相对稳定性增强; 最后对比分析KMgn, NaMgn(n=1-12)的二阶能量差分和劈裂能发现; 在n=6时,两种团簇的相对稳定性都较强,但KMg6团簇的稳定性优于NaMg6团簇.

团簇； 能量； 第一性原理； 结构

1 引 言

团簇科学研究的基本问题是弄清团簇如何由原子、分子一步一步发展而成, 以及随着这种发展, 团簇的结构和性质如何变化, 当尺寸多大时, 发展成宏观固体. 团簇科学是一个具有丰富科学内涵的交叉学科, 正方兴未艾[1-8]. 团簇研究是化学和物理两大学科之间的一个新的生长点, 它涉及量子化学、天体物理、生命科学、材料科学和纳米技术等许多领域, 是纳米材料和工程的基础, 也将是今后几十年材料科学的主要推动力之一. 近年以来, 金属团簇无论在实验还是理论计算上都已经得到了广泛的研究. 随着团簇研究的深入, 团簇的掺杂对主体团簇的结构和电子性质的影响备受人们关注.田付阳等对镁团簇中掺入铝原子的几何结构、电子结构进行研究发现:铝原子掺入均能使镁团簇的平均结合能增大, 稳定性增强；而铝原子的诱导, 使AlMgn在n<8时, 掺杂镁团簇中镁原子3P轨道上的NBO电荷分布大于纯镁团簇[2]；同时陈玉红等人对MgmBn(m=1, 2;n= 1-4)团簇结构与性质的密度泛函理论研究发现团簇的最稳定结构是平面结构, 团簇的稳定结构中通常是几个呈负电性的B原子形成一个负电中心, 而其他B原子和Mg原子通常处在端位且显正电性[3]；姚建刚[4]等采用第一性原理研究了NiMgn(n=1-12)团簇, 结果发现NiMg6基态结构具有很高的对称性Oh, 很好的稳定性和化学活性, 能隙仅为0.25 eV；然而对镁团簇掺K和掺Na少有报道, 所以基于此种情况我们在镁团簇的基础上分别掺入活跃金属钾(K)和钠(Na)来研究XMgn(X=K, Na;n=1-12)团簇的几何结构和性质.

2 研究方法

本文基于第一性原理在自旋极化上对XMgn团簇的结构进行了设计与优化, 在广义梯度近似(GGA)下, 选择带极化的双数值原子基组(DNP)和自旋非限制近似(SCF)求解自洽场[4-7].几何结构优化位移量收敛标准取0.05 nm, 原子间作用力收敛标准取0.020 Hartree/nm, 能量收敛标准取2×10-5Hartree,自洽场收敛标准取10-6Hartree[7-10].同时为了验证所选方法的可靠性, 我们在相同的条件下计算了Mg2的键长、平均结合能等物理量. 计算结果表明:Mg2键长值为0.4060 nm, 与文献[1]的计算值0.41439 nm基本一致；所以可以确定采用的方法是可靠的.

3 结果与讨论

3.1 几何结构

通过计算和优化得到KMgn, NaMgn(n=1-12)的几何结构, 图1和图2分别列出了它们的最低能量的几何结构；其中, 绿色的小球表示镁原子, 紫色表示掺入的钾原子和钠原子.

图1 KMgn(n=1-12)团簇的最低能量结构Fig.1 Optimized geometries of KMgn (n=1-12) clusters

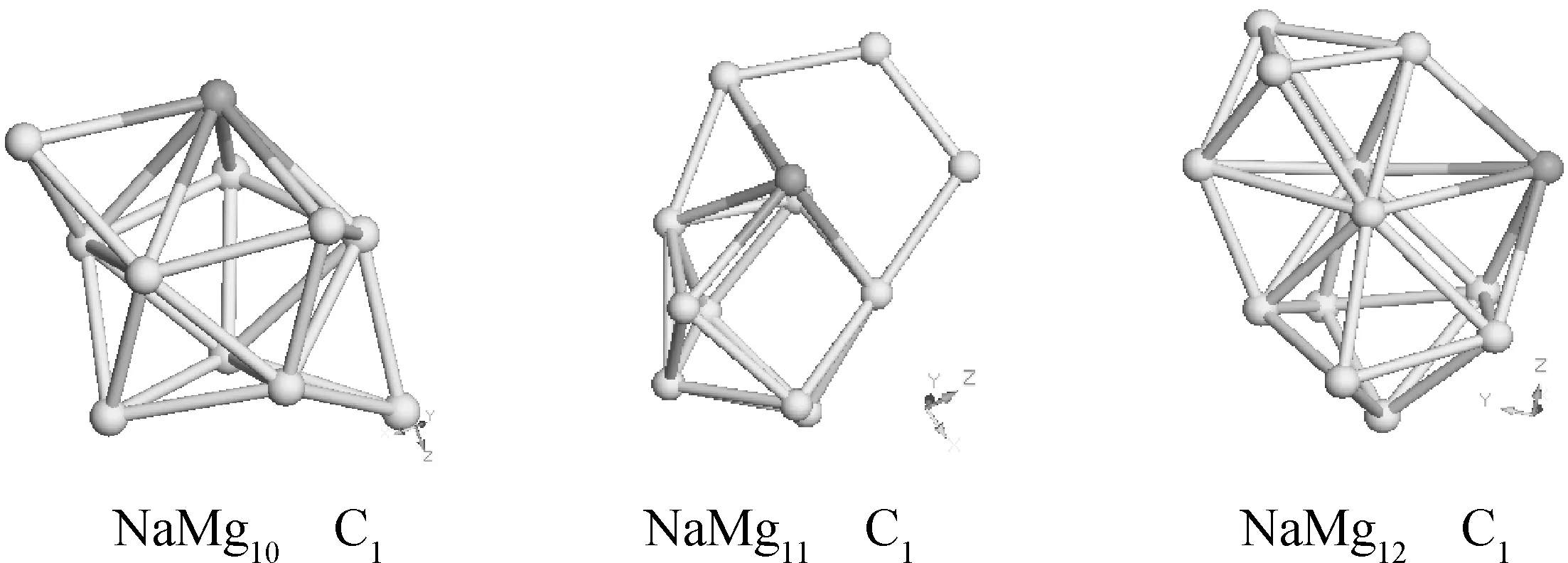
图2 NaMgn (n=1-12)团簇的最低能量结构Fig.2 Optimized geometries of NaMgn (n=1-12) clusters

对于KMg2三原子团簇, K-Mg-K之间的键角为180°, 所以该团簇呈直线结构, 它的结构比较简单；具有Dinfh对称性, 键长(K-Mg)为0.3420 nm. KMg3键长为0.3420 nm, Mg-K-Mg的夹角为120度, KMg4团簇中K-Mg键长为0.3421 nm, 其中Mg-K-Mg之间的夹角为109度, 是具有C3v对称的的的立体图; KMg5是Cs对称, 它是在KMg4团簇的基础上增加了一个镁原子而构建起来的, 但对称性却由C3v变为Cs; 对于KMg6团簇, 钾和镁之间的最短键长为0.3420 nm, KMg6团簇的稳定态具有C2v对称性. KMg7团簇却是在KMg6团簇的基础上加了一个镁原子得到的, 它具有CS对称性. KMg8是在KMg7团簇的基础上加了一个镁原子, 团簇虽然是最低能量结构, 但原子构型很松散. 从图1可以看出, 随着原子数的增加, 团簇的结构呈笼状结构, 在n=10-12时, 团簇K-Mg键长都比较长, 在KMg12团簇中, 钾原子进入团簇的内部且呈现出逃逸的趋势.

NaMg2团簇Na-Mg键长0.3014 nm,夹角为53.9度的等腰三角形, 它具有C2V对称性; NaMg3的键长为0.3005 nm, Mg-Na-Mg的夹角为62.917度, 3个镁原子和一个钠原子构成了一个近似四面体；它具有C3V对称性;NaMg4团簇中Na-Mg之间的键长为0.3020 nm, 它具有C1对称性, 它是在NaMg3团簇的构形上增加了一个镁原子而来的; NaMg5是在团簇NaMg4的基础上增加一个镁原子, 他的束缚能为-1.85858 eV, 束缚能也增加了-0.50406 eV;然而我们还可以注意到NaMg5团簇可以在KMg4团簇的亚稳态的基础上增加一个镁原子, 但束缚能从KMg4团簇的亚稳态的-1.31173 eV增加到-1.85858 eV, 束缚能增加了-0.54685; NaMg6团簇稳定结构与KMg6的稳定结构相似, 但键长略有差异, 它具有C2V对称性；NaMg7团簇的稳定态是在Mg8团簇正十面体的模型上用钠原子替换镁原子得来, 它具有C1对称性.NaMg8团簇具有CS对称性；在n=10-12时, NaMgn团簇的结构模型都是在NaMg8团簇的结构上增加镁原子和替换镁原子得到的. 总之,n小于6时, 团簇的构造都相对简单；在n大于6时, 团簇的结构呈现出比较复杂的立体结构.

3.2 KMgn, NaMgn(n=2-12)团簇的稳定性分析

从图5的束缚能看, NaMgn(n=2-12)团簇的束缚能是按照一定的差呈有序下降的曲线, 表明该团簇的稳定性随着n的增大而增强；而KMgn(n=2-12)团簇的束缚能在n=4, 5, 7, 8, 9, 12时出现较大的波动, 表明KMgn(n=2-12)团簇的稳定性不强, 从KMgn团簇结构上看, 在n=4, 5, 7, 8, 9, 12时K原子被Mg原子包裹, 随着n的增加K原子渐渐的进入到笼状结构中, 而K-Mg之间的结合键长比较长, 所以导致KMgn团簇了在n=4, 5, 7, 8, 9, 12时结构不稳定, 特别是KMg12团簇的稳定性较差.

在研究不同尺寸的团簇的相对稳定性时, 本文采用了二阶能量差分和劈裂能来表征团簇的相对稳定性, 公式如下:

△2E=E(XMgn+1)+E(XMgn-1)-2E(XMgn)D(n,n-1)= E(XMgn-1)+ E(Mg)- E(XMgn)

从图3的曲线的变化趋势来看,KMgn, NaMgn(n=1-12)团簇的二阶能量差分值都出现不同幅度的波动；分析NaMgn(n=1-12)团簇的二阶能量差分, 随着团簇的不断增大, 二阶能量差分在n=6, 7, 9, 10处, 出现一定的波动, 在n=6, 10时, 团簇的二阶能量值出现峰值, 也就是说在n=6, 10时, 该团簇的相对稳定性较强, 但就NaMgn(n=1-12)团簇而言, 其二阶能量差分值都波动不大；所以, 在纯镁团簇中掺入钠元素, 对其稳定性的影响不大. 对 KMgn(n=1-12)团簇的二阶能量差分分析发现, 在n=3, 6, 11时, 团簇的二阶能量值出现峰值, 也就是说在n=3,6, 11时, 该团簇的相对稳定性较强.对比分析KMgn, NaMgn(n=1-12)的二阶能量差分；我们发现:在n=6时, 两种团簇的相对稳定性都较强, 但KMg6团簇的稳定性优于NaMg6团簇；同时也发现KMgn(n=1-12)的二阶能量差分的波动较大, 说明在纯镁团簇中掺入钾元素, 对其稳定性的影响较大.

在图5中可以看到KMgn, NaMgn(n=1-12) 团簇的劈裂能都出现不同幅度的波动；对于NaMgn(n=1-12)团簇的劈裂能, 随着团簇的原子数不断增多, 劈裂能出现一定的波动；在n=6, 8, 9时, 团簇的劈裂能出现峰值, 表明在n=6, 8, 9时, 该团簇的相对稳定性增强；对 KMgn(n=1-12)团簇的劈裂能分析发现, 在n=3, 6, 10时, 团簇的劈裂能出现峰值, 也就是说在n=3, 6, 10时, 该团簇的相对稳定性较强.对比分析KMgn, NaMgn(n=1-12)的二阶能量差分与劈裂能,我们发现:对于NaMgn(n=1-12)团簇而言在n=6, 9时, 团簇的二阶能量差分和劈裂能都出现峰值, 表明在n=6, 9时团簇的相对稳定性增强, 对于KMgn(n=1-12)团簇而言在n=6, 10时, 团簇的二阶能量差分和劈裂能都出现峰值, 表明在n=6, 9时团簇的相对稳定性增强.

表1 KMgn、NaMgn(n=2-12)团簇的束缚能

Table 1 The binding energygaps of the grounp states for KMgn, NaMgn(n=2-12)

nKMgn(eV)NaMgn(eV)nKMgn(eV)NaMgn(eV)2-0 26819-0 295638-2 62752-3 824753-0 91080-0 895739-3 74718-4 769024-0 31156-1 3545210-5 64336-5 480135-0 62787-1 8585811-6 14568-5 841096-2 85047-2 4890712-4 54083-6 360277-2 58131-2 93542

图3 KMgn, NaMgn (n=1-12)团簇的束缚能随原子数的变化关系Fig.3 The binding energy changes with the increasing number of atom in the KMgn, NaMgn (n=1-12) clusters

表2 KMgn,NaMgn(n=1-12)团簇的总能量Et

Table 2 The total energygaps of the grounp states for KMgn, NaMgn(n=1-12) clusters

nKMgn(Et/eV)NaMgn(Et/eV)n2-1000 1142053-562 45537723-1200 2177836-762 55706714-1400 2757248-962 65356365-1600 3673115-1162 75172406-1800 5168474-1362 85453067-2000 5990246-1562 95056998-2200 6806854-1763 06288859-2400 8017862-1963 177221310-2600 9514409-2163 282995611-2801 0498636-2363 379272612-3001 0708436-2563 4746129

图4 KMgn , NaMgn (n=1-12)团簇的二阶能量差分Fig.4 The second order energy differences of the KMgn, NaMgn (n=1-12) clusters

图5 KMgn, NaMgn (n=1-12) 团簇的劈裂能Fig.5 The fragmentation energies of the KMgn, NaMgn (n=1-12) clusters

4 结 论

对于KMgn(n=1-12) 团簇, 在n>5时, 其几何结构转变为笼状；在n=12时, K原子进入到团簇的内部, 由于K原子与Mg原子所形成的键比较长, 所以K原子在团簇内部呈逃逸的趋势. 对于NaMgn(n=1-12) 团簇,在n<6时, 团簇的构造都相对简单；在n大于等于6时, 团簇的结构呈现出比较复杂的立体结构, 但Na元素的掺入对团簇的几何结构影响较小.

对于NaMgn、KMgn(n=2-12)团簇的稳定性而言:NaMgn(n=2-12)团簇的束缚能随着n的增大呈直线下降, 其稳定性增强；KMgn(n=2-12)团簇的束缚能在n=4, 5, 7, 8, 9, 12时出现较大的波动, 表明在n=4, 5, 7, 8, 9, 12时团簇稳定性不强. 分析NaMgn、KMgn(n=1-12)团簇的二阶能量差分和劈裂能发现:NaMgn(n=1-12)团簇在n=6, 9时, 团簇的二阶能量差分和劈裂能都出现峰值, 表明在n=6, 9时团簇的相对稳定性增强；KMgn(n=1-12)团簇在n=6, 10时, 团簇的二阶能量差分和劈裂能都出现峰值, 表明在n=6, 9时团簇的相对稳定性增强；同时对比分析KMgn, NaMgn(n=1-12)的二阶能量差分和劈裂能发现, 在n=6时, 两种团簇的相对稳定性都较强, 但KMg6团簇的稳定性优于NaMg6团簇.

[1] Fu Q S, Sheng Y, Tu M J. Geometical and electronic properties of Mgn(n=2-7) clusters [J].JournalofSichuanUniversity, 2006, 43(5): 1056 (in Chinese) [附青山, 盛勇, 涂铭旌. Mgn(n=2-7)团簇几何结构研究[J]. 四川大学学报, 2006, 43(5): 1056]

[2] Tian F Y, Wang Y X, Jin Q,etal. Density functional theory study of structures and electronic properties of XMgn(X=B, Al,n=1-12) clusters [J].ActaPhysicaSinica, 2008, 57(3): 1648 (in Chinese) [田付阳, 王渊旭, 井群, 等. 第一性原理对XMgn(X=B, Al,n=1-12)团簇的几何结构和电子性质的研究[J]. 物理学报, 2008, 57(3): 1648]

[3] Chen Y H, Zhang C R, Ma J. Density functional theory study on the structure and properties of MgmBn(m=1, 2;n=1-4)clusters[J].ActaPhysicaSinica, 2006, 55(1): 171 (in Chinese)[陈玉红, 张材荣,马军. MgmBn(m=1, 2;n= 1-4)团簇结构与性质的密度泛函理论研究[J]. 物理学报, 2006, 55(1): 171]

[4] Yao J G, Wang X W, Wang Y X,etal. First principles study of the NiMgn(n=1-12) clusters [J].ActaPhysicaSinica, 2008, 57(7): 4166 (in Chinese)[姚建刚, 王献伟, 王渊旭, 等. NiMgn(n=1-12)团簇的第一性原理研究[J]. 物理学报, 2008, 57(7): 4166]

[5] Lee J S. Basis-set limit binding energies of Benand Mgn(n=2,3,4) clusters[J].Phys.Rev. A, 2003, 68: 043201.

[6] Cheng Z F, Xiao X Y. Electric structure and stability of (Sc)12X cluster (B, C, N, Al, Si, P)[J].J.At.Mol.Phys., 2007, 24(3): 564 (in Chinese) [程正富, 肖绪洋. (Sc)12X团簇(B, C, N, Al, Si, P)电子结构与稳定性[J]. 原子与分子物理学报, 2007, 24(3): 564]

[7] Wei L, Yang Z, Yan Y L,etal. Density-functional study of ground structures and electronic properties of Li2Ben(n=1-10) clusters [J].J.At.Mol.Phys., 2007, 24(5): 1009 ( in Chinese)[魏凌, 杨致, 闫玉丽, 等. 第一性原理计算Li2Ben(n=1-10)团簇的最低能量结构及其电子性质[J]. 原子与分子物理学报, 2007, 24(5): 1009]

[8] Zope R R, Baruah T. Conformers of Al13, Al12M, and Al13M(M=Cu, Ag, and Au) clusters and their energetics [J].Phys.Rev. A, 2001, 64: 053202.

[9] Fournier R, Cheng J B Y, Wong A. Theoretical study of the structure of lithium clusters [J].J.Chem.Phys., 2003, 119: 9444.

[10] Lee C, Yang W, Parr R G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density[J].Phys.Rev. B, 1988, 37: 785.

First principle study of structures and properties of XMgn
(X=K, Na,n=1-12) clusters

FU Chun-Ping, SUN Ling-Tao, CHENG Zheng-Fu

(Department of Physics, Chongqing University of Arts and Sciences, Chongqing 402160, China)

The structures and electronic properties of XMgn(X=K, Na;n=1-12) clusters have been researched by mean of the generalized gradient approximation (GGA) of first principle. It is shown that the KMgn(n=1-12) cluster’s geometric construction change into cage withn>5, and the K atom will be escaping tendency as n=12; while KMgn(n=1-12) clusters’ relative stability is improved whennis equal to six and nine. Withn>5, the structures of the NaMgn(n=1-12) clusters are relatively simple, but the structures are changed to complicated three-dimensional withnis equal or greater than 6; as well as NaMgn(n=1-12) clusters’ relative stabilities are improved whennis equal to six and nine. At last, by analyzing and comparing the second order difference energy and splitting energy between KMgnand NaMgn(n=1-12), we find that the two clusters’ relative stabilities are improved whennis equal six, but the stability of KMg6is superior to NaMg6cluster.

Cluster; Energy; First principles; Structure

2014-04-16

重庆文理学院校级校级科研项目(Z2013KJ17); 永川区自然科学基金(Ycstc, 2014nc4002)

伏春平(1986—)，男，藏族，四川平武人，硕士，助教，主要从事材料物理的研究.E-mail: fuchunping@163.com

程正富.E-mail: chzhfu8@163.com

103969/j.issn.1000-0364.2015.08.012

O641

A

1000-0364(2015)08-0597-06