基于二元矢量阵的相干源分辨性能研究

张 锴

(中国电子科技集团公司第20研究所，西安 710068)



基于二元矢量阵的相干源分辨性能研究

张 锴

(中国电子科技集团公司第20研究所，西安 710068)

相干源的存在使矢量阵的高分辨方位估计性能严重恶化。分析了单矢量传感器的阵列流型，结合空间平滑算法的应用条件，给出了基于二元矢量阵的最小方差无失真响应(MVDR)和多重信号分类(MUSIC)解相干算法，研究了算法的性能。理论分析和仿真实验证明该算法可实现对相干源的到达方向(DOA)估计，在相同信噪比条件下，相较于MVDR算法、MUSIC算法具有更好的方位分辨力，受到相干源之间方位夹角的影响更小，而且对相干源之间的强度差异不敏感。

二元矢量阵；相干源；最小方差无失真响应；到达方向估计

0 引 言

矢量传感器可以同时、共点地拾取空间的声压与振速信息，其工程应用也受到了越来越多的关注。M.Hawkes和A.Nehorai首先把最小方差无失真响应(MVDR)波束形成的思想扩展到声矢量阵，使阵列具有了左右舷分辨的能力[1]。K.T.Wong和M.D.Zoltowski提出了速度场波束域自初始化多重信号分类(MUSIC)方法[2]，从而使矢量传感器和高分辨率方位估计结合的研究迅速展开[3-4]。

通常情况下，较大的阵列尺度是阵列实现高分辨率的关键因素，可是水下平台往往体积有限，使得水下设备往往不能有大的基阵尺度，同时，水下干扰源复杂，往往需要在多干扰的低信噪比环境中对目标进行探测和跟踪，尤其相干源的存在更是导致了高分辨方位估计性能的严重恶化[5-7]。

（2）学生在调查中对在课堂内开展文化主题教学活动表示出相当的兴趣。在课堂教学进入文化主题环节时，采用互动活动的方式进行，如分组讨论、模拟演示等。活动准备工作由学生在课前预先做好，疑难问题在活动中面对面答疑。学生可使用视频、图片等多媒体方式展示，使文化导入在课堂内互动性更强，更有趣味，也更直观易懂。

前人在这方面做了很多工作，文献[8]、[9]中作者提出了利用虚元技术和恒定束宽相结合方法，提高了小尺度阵列的多目标跟踪能力并且实现了对相干源的分辨，但是其算法较为复杂，文献[10]则是利用基于矢量传感器的时间反转镜技术实现了基于二元矢量阵的目标被动定位，但其定位精度受建模误差的影响较大。注意到文献[11]指出若2个相干信号同时进入不同阵列时其协方差矩阵之和的秩有可能不亏损这一论述，本文结合单矢量传感器高分辨方位估计原理和空间平滑技术，对二元矢量阵的解相干性能进行深入分析研究。

(4)坡型指标量化及归一化。坡型一般采用斜坡的曲率进行描述。曲率≥0的斜坡为直线型坡和凸型斜坡，其发生变形破坏的可能性较高；曲率<0的斜坡为凹型坡和阶梯型坡，其发生变形破坏的可能性较低。根据曲率的大小进行0～1之间的线性归一化处理，得到坡型指标归一化结果(图3d)。

1 理论基础

1.1 二元矢量阵的模型

仅考虑二维情况，即矢量传感器输出共点的声压p和振速vx及vy。假设相干信号为单频信号，二元矢量传感器的阵元间距为半波长λ/2，则远场条件下阵元在t时刻的接收信号表示为：

Xi(t)=A(θ)DiS(t)+N(t)

(1)

(2)

式中：Xi(t)为第i个阵元接收快拍数据模型；Di为第i个阵元的2×2维对角线矢量；α、β分别为相干信号x1(t)和x2(t)在第2个阵元上的相位延迟，对于单频相干信号，α、β的值与频率和入射方位角有关；ak(θk)为第k个相干信号的方向矢量；θk为该信号的水平入射角，满足：

(3)

1.2 基于单矢量传感器的MVDR和MUSIC方位估计

(4)

A(θ)=[a1(θ1)a2(θ2)]

“不如我把书放回去，反正没人看见。即使被发现了，也不会知道是我撕破的。”她怀着一丝侥幸，悄悄将书放回书架。接着，伏尼契继续寻找下一本书看，尽量远离刚刚被自己损坏的那本书。

(5)

式中：第1和第2个分量对应于矢量传感器2个振速通道输出，最后一个分量对应于矢量传感器声压通道输出。

1.3 基于空间平滑的二元矢量阵相干源分辨算法

本研究提示，规模化猪场要重视种猪的选育，避免“重引种轻选育”的错误思想。选留种猪要有科学依据，这就要求准确测量和记录繁殖相关基本数据，如母猪的妊娠期、初生窝重、产仔数、产活仔数和断奶窝重等指标，数据测量要持续到第三胎以上，定期进行统计分析，实行体型外貌和选择指数相结合的方法综合选留种畜，真正提高猪场的经济效益和生产效率。

此时2个阵元的数据协方差矩阵分别为：

(6)

(7)

式中：RS为信号协方差矩阵。

由于入射两信号为相干信号，满足x2(t)=ηx1(t)ejφ，其中η是功率系数，φ是相位差，所以:

(8)

此时RS为非满秩矩阵。需要指出，本文中定义的阵列流型为单矢量传感器自身具有的三维方向矢量ak(θk)，没有时延参量而只与信号的入射方向有关。

S(t)=[x1(t)x1(t)]

MVDR波束形成器，即最小方差无失真响应波束形成器，其准则是在保持观测方向上的信号功率不变情况下，使噪声以及来自非信号方向的任何干扰所贡献的功率为最小，其谱估计公式为[12]：

(9)

通过对大型卧式加工中心床身铸件进行的实型消失模工艺设计、切活料填砂设计及关键过程控制等，总结了生产此类铸件的铸造工艺及质量的控制要点，得到了合格的铸件，为此类铸件的批量生产提供了技术支持。

对矢量传感器接收的数据协方差矩阵进行特征分解得到的信号子空间与噪声子空间是正交的，即入射信号的导向矢量a(θ)与噪声子空间正交。得到MUSIC谱估计公式如下[12]：

(10)

式中：UN为对单矢量传感器的数据协方差矩阵R特征分解得到的噪声子空间。

下面将通过仿真进一步验证所述理论。仿真中的噪声是零均值的高斯噪声，相干源信号为2个同频单色信号，采样频率5kHz，样本点数5 000，搜索步长Δθ=0.1°，计算结果为100次独立实验的统计数据，如无特别说明,上述仿真条件不变。

(11)

注意到，若仅保留上式分母括号中的第2项，则类似式(10)的表达式：

(12)

可见，MUSIC算法属于噪声子空间算法，而MVDR算法属于信号子空间算法[12]，在后面同时给出了2种算法的仿真结果。

山东省东营市东营区是吕剧的发祥地，一代又一代艺人不断致力于吕剧的传承、弘扬。雅俗共赏的吕剧已成为东营人田间地头、堂前屋后、广场剧场演唱的一门群众艺术。在现代多元文化的影响下，随着一些老艺人相继去世，40岁以下年轻人群体渐不知吕剧为何物。因此，有必要对国家级非物质文化遗产吕剧文化的发展壮大，对吕剧在实施“黄蓝”国家战略背景下发挥其作用，促进产业转型升级等进行思考和研究探讨。

考虑到信号源相干时会导致信号子空间的维数小于信号源数，从而无法正确估计信号源方向，故本节将讨论如何利用空间平滑原理实现上述2种算法对相干信号源的分辨。众所周知，空间平滑算法是针对一般高分辨算法不能解相干而提出的一种有效方法[12], 它在一般情况下只适用于均匀线阵，而前向空间平滑的基本思想是将等距线阵分成若干个相互重叠的子阵列，通过各子阵列的协方差矩阵的平均运算来实现解相关。相应地对于二元矢量阵，考虑到当子阵阵元数目不小于目标数目，且子阵数目不小于目标数目，采用空间平滑的数据协方差矩阵Rf是满秩的情况，得到：

式中：a(θ)为导向矢量；在本文中定义R为单个矢量传感器接收的3×3维数据协方差矩阵。

(13)

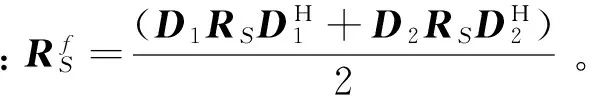
此时对数据协方差矩阵Rf特征分解，利用式(9)～(10)即可得到基于空间平滑的空间谱估计。由此看出，与传统的空间平滑算法相比，本文方法不仅有效利用了阵元之间的相位信息，还充分考虑了矢量传感器自身具有的3×1维阵列流型特点。

2 仿真分析

观察发现，式(9)中数据协方差矩阵进行特征分解可得：

首先考察本文算法的有效性，相干源θ1=30°，θ2=60°，f1=f2=500 Hz，信噪比为30dB，图1、图2分别示出传统MVDR和MUSIC算法与本文算法得到的空间谱。仿真结果表明，在相同信噪比条件下，本文算法均可以实现相干源的分辨，而传统算法不具备分辨相干源的能力，从而说明本文提出的基于空间平滑的二元矢量阵解相干算法具有相干源的分辨能力。

图1 传统MVDR算法和本文算法MVDR性能比较

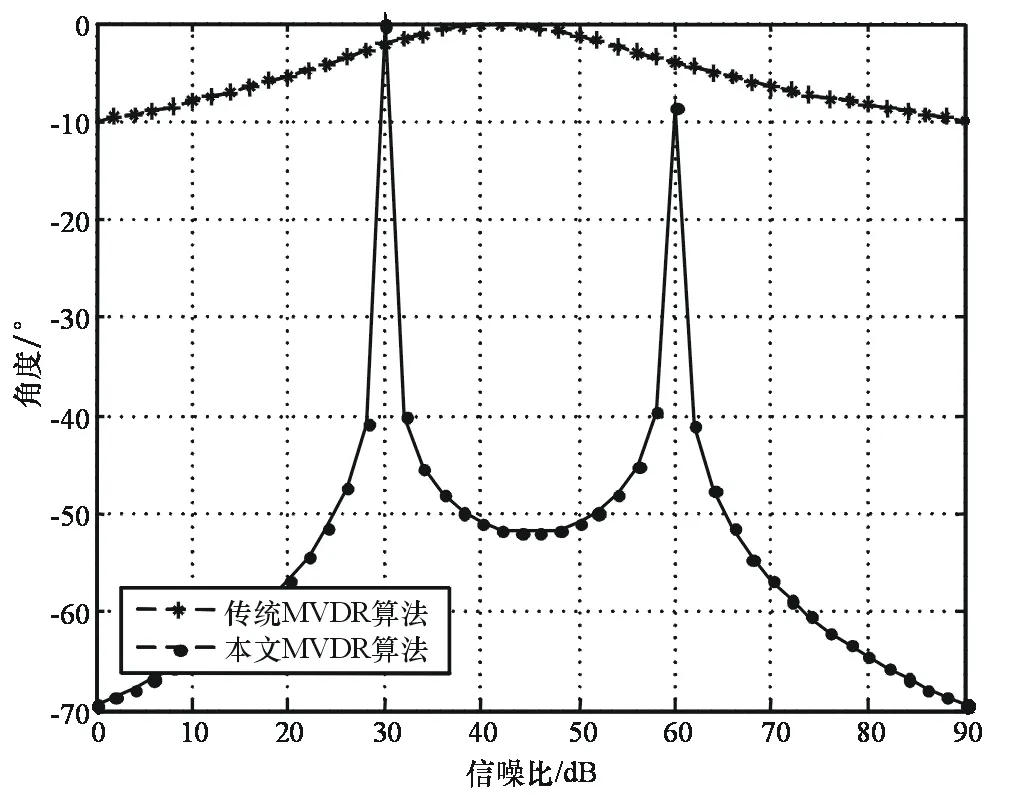
图2 传统MUSIC算法和本文算法MUSIC性能比较

考察信噪比对算法性能的影响，θ1=30°，θ2=60°，f1=f2=500 Hz，且相干源的功率相等，图3、图4分别示出了不同信噪比条件下2种算法得到的空间谱。仿真结果表明，随着信噪比的提高，MVDR算法的谱峰宽度逐渐变窄，分辨力也逐渐提高。相较于MVDR算法，在相同信噪比条件下，MUSIC算法对相干源的谱峰宽度更窄，多目标的分辨能力更好。

图3 信噪比不同时MVDR的算法性能

图4 信噪比不同时MUSIC的算法性能

接下来考察相干源功率不相等情况下的算法性能，目标1满足θ1=30°，信噪比为35dB。图5、图6则分别示出了相干源强度差异不同条件下2种算法得到的空间谱。

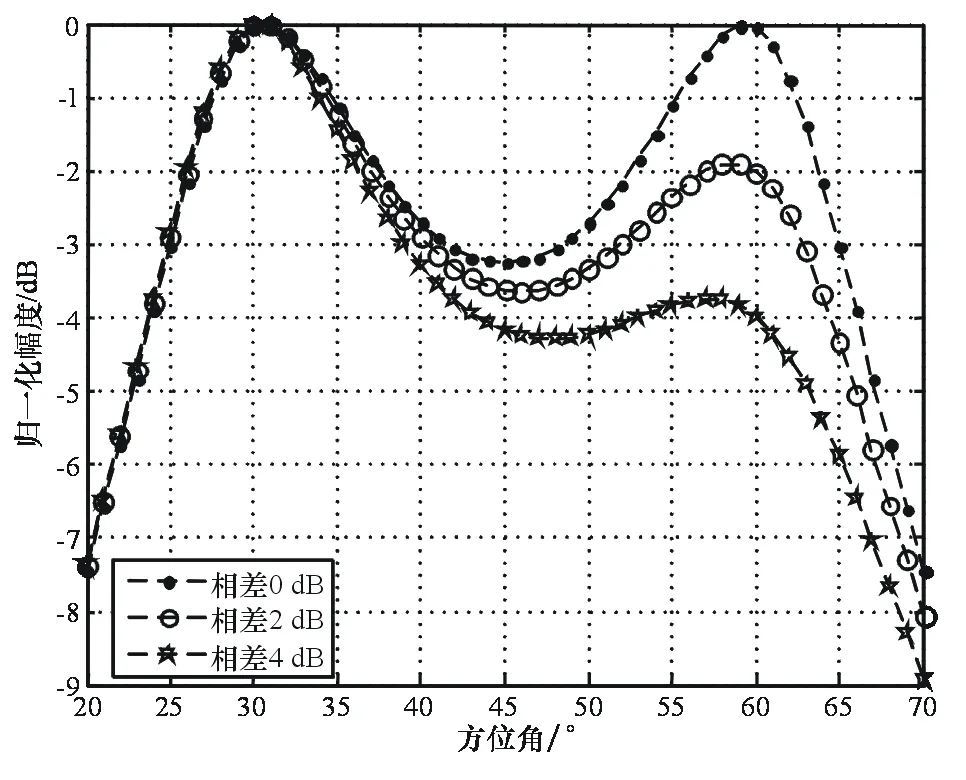
图5 功率不相等时MVDR的算法性能

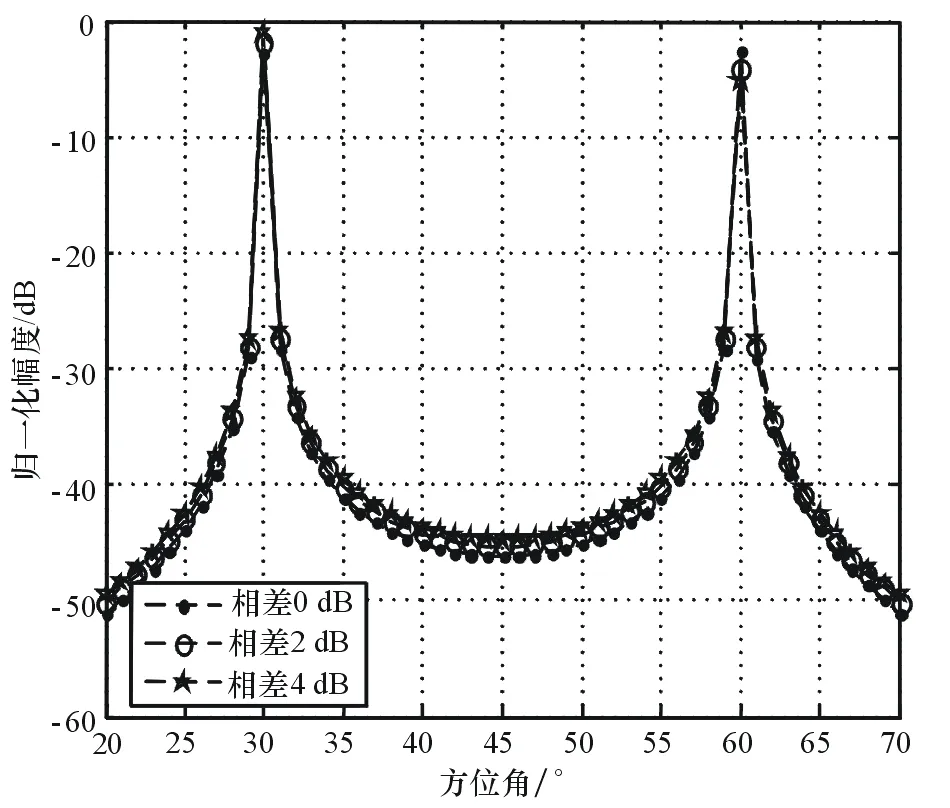
图6 功率不相等时MMUSIC的算法性能

仿真结果表明，在仿真信噪比条件下，随着相干源之间强度差异的减小，基于MVDR算法的谱峰宽度也逐渐变窄。相比之下，MUSIC算法受到相干源之间强度差异的影响则较小，方位分辨力很高。

我们赶回河浦时天刚擦黑。路边田里姜月娥在割稻子，她冲我喊道，腊枝你快点儿回去！你伢儿病得么事样的，把百福寺的先生都接来了！我听了心里一紧，拔腿就跑，匆忙赶回屋里。大梁蹲在摇篮边，抬起紧锁的眉头，求救似的望着我。我跑过去，双手扒着摇篮，见大女儿小脸儿潮红，紫色的小嘴儿开张着，透亮的鼻翼费力地翕动，呼呼地直喘气。我把大女儿抱起喂奶，她小脸儿贴在我胸前，嘴巴一动不动！我慌了神，把奶头儿硬往她口里塞。她就那样懒洋洋地噙着，像是噙着一粒石子、一颗土块，无动于衷！

最后考察方位夹角的变化对算法能的影响，相干源的功率相等，信噪比为25dB，且满足目标1的方位θ1=30°，图7、图8分别示出了相干源在不同方位夹角下2种算法得到的空间谱。

图7 不同夹角下基于MVDR的算法性能

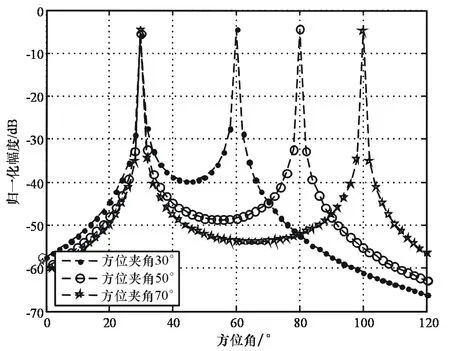
图8 不同夹角下基于MUSIC的算法性能

仿真结果表明，在仿真条件下随着方位夹角变小，MVDR算法的谱峰宽度变宽，而且当夹角为30°时只能得到合成声能流的方位估计。对于MUSIC算法而言，在仿真条件下受到夹角的影响较小，不同夹角情况下仍具有很窄的谱峰宽度。

3.教学活动处理不当。一方面教师对转化体育后进生思想认识不足；另一方面现今体育教师教学任务重，课时多，班级人数多，限于时间和精力关系对体育后进生照顾关心不够；此外，部分体育项目本身具有一定难度和危险性，学生由于偶然事故受伤，就会产生“一朝被蛇咬，十年怕井绳”的心理，对所有体育活动都存在被动、恐惧的抵制心态。

（1）山羊感染率。在如东县不同地区采集的80份山羊粪便中，有67只羊感染球虫，感染率为83.75%（67/80）。

3 结束语

本文对二元矢量阵的解相干算法的性能进行了分析，考察了相干源的信噪比、相干源之间声强级差异以及相干源之间方位夹角等因素对算法性能的影响，得到了一些有意义的结论。

本文方法中仅依靠2个矢量传感器，在一定条件下完成对2个相干源目标的分辨，实现了矢量阵对相干源分辨的小尺度化。同时将空间平滑算法应用到二元矢量阵的解相干中，拓展了空间平滑算法的应用范围。考虑到工程上的应用，本文算法的稳健性尚有待进一步研究与验证。

[1]HawkesM,NehoraiA.Acousticvector-sensorbeam-formingandCapondirectestimation[J].IEEETransactionsonSignalProcessing,1998(9):2481-2491.

[2]WongKT,ZoltowskiMD.Self-initiatingMUSIC-baseddirectionfindinginunderwateracousticparticlevelocity-fieldbeamspace[J].IEEEJournalofOceanicEngineering,2000,25(2):262-273.

[3] 徐海东,梁国龙,惠俊，等.解析声能流Capon空间谱估计[J].声学技术,2004(3):178-182.

[4] 徐海东.基于声矢量阵的高分辨方位估计技术研究[D].哈尔滨：哈尔滨工程大学,2004.

[5] 郡社锋,马远良，侯朝焕，等.宽带波束域相干信号子空间高分辨方位估计[J].声学学报,2006(5)：418-424.

[6]ChenYM,LeeJH.Estimatingtwo-dimensionalanglesofarrivalincoherentsourceenvironment[J].IEEETransactionsonAcoustics,SpeechandSignalProcessing,1989,37(1):153-155.

[7]ChenYH,LianYT.2-Dmultitargetangletrackingalgorithmusingsensorarray[J].IEEEProceedings,PartF:RadarandSignalProcessing,1995,142(8):158- 161.

[8] 江磊.小尺度阵信号处理技术研究[D].哈尔滨：哈尔滨工程大学,2008.

[9] 付彦.基于小尺度矢量阵的多目标分辨研究[D].哈尔滨：哈尔滨工程大学,2009.

[10]惠俊英，马敬广，李峰，等.二元阵被动时间反转镜定位技术研究[J].哈尔滨工程大学学报,2007(11):1247- 1251.

[11]ShanT,WaxM,KailathT.Onspatialsmoothingfordirect-of-arrivalestimationofcoherentsignal[J].IEEETransactionsonASSP,1985(6):806-811.

[12]王永良.空间谱估计理论与算法[M].北京：清华大学出版社,2004.

Research into The Coherent Sources Resolution Performance Based on Dualistic Vector Array

ZHANG Kai

(The 20th Research Institute of CETC，Xi'an 710068，China)

The existence of coherent sources makes the high-resolution azimuth estimation performance get worse badly.This paper analyzes the array manifold of single vector sensor,combining the application conditions of spatial smoothing algorithm,presents the de-correlation algorithm of minimum variance distortionless response (MVDR) and multiple signal classication (MUSIC) based on dualistic vector array,studies the algorithm performance.The theory analysis and simulation experiment prove that the direction of arrival (DOA) estimation of coherent sources can be realized by the algorithm,comparing with the MVDR algorithm and MUSIC algorithm,this algorithm has better azimuth resolution,is affected at the azimuth angular separation between coherent sources weakly and insensitive on the diversity between coherent sources in the same signal noise ratio.

dualistic vector array;coherent sources;minimum variance distortiontess response;direction of arrival estimation

2015-03-11

TB566

A

CN32-1413(2015)02-0067-05

10.16426/j.cnki.jcdzdk.2015.02.018