基于叠加Chirp信号的载波频率捕获方法研究

韩 磊，程乃平，丁 丹

(1.装备学院,北京 100416；2.北京空间信息中继传输技术研究中心,北京 100094)



基于叠加Chirp信号的载波频率捕获方法研究

韩 磊1,2，程乃平1，丁 丹1

(1.装备学院,北京 100416；2.北京空间信息中继传输技术研究中心,北京 100094)

以Chirp信号作为参考序列，以弱功率直接与成型滤波后的有用数据叠加，然后经载波调制发送，节约了带宽资源和功率资源。在接收端利用Chirp信号的恒包络性和Chirp信号在相应分数阶傅里叶域的时频聚集特性，对接收信号进行分数阶傅里叶变换(FRFT)，搜索到峰值坐标、完成Chirp信号参数估计，从而得出载波的多普勒频偏和频偏变化率，完成载波捕获，并抵消掉叠加信号，经仿真验证，该理论方法可行。

Chirp信号；分数阶傅里叶变换；参数估计；载波捕获

0 引 言

无线电通信系统中，载波频率同步是载波同步的关键技术，是正确接收并解调出有效数据的前提。载波频率捕获，即对接收载波的多普勒频偏及频偏变化率进行准确的参数估计和补偿，通常采用插入训练序列的方式辅助完成载波频偏估计，实现通信同步。如文献[1]提出了一种在正交频分复用(OFDM)系统中插入2个前后极性相反的训练序列，使定时同步测量时只出现一个相关峰，提高了频偏估计的性能；文献[2]采用了在有用信号前插入2个PN序列，利用相关特性在时域完成频偏的估计和修正；文献[3]以Chirp信号作为训练序列，利用Chirp信号在分数阶傅里叶域的能量聚集特性来完成频率的参数估计[4]和补偿。以上方法均是将训练序列作为同步头，以一定时间间隔插入有用信号当中，这样一方面降低了传输效率，另一方面也破坏了信号的保密性。本文提出在发送端用Chirp信号作为参考信号直接与有用数据弱叠加的方法，叠加后不改变Chirp信号时频聚集特性，在接收端对传输信号进行分数阶傅里叶变换(FRFT)，利用Chirp信号能量汇聚作用进行参数估计完成载波频率捕获。

1 Chirp信号的FRFT与参数估计

Chirp信号是一种典型的非平稳信号，在雷达和声纳等技术领域有广泛应用，也十分适合作为一种同步参考信号用于通信系统，经过适当的时频变换(如Wigner-Hough变换、FRFT或匹配傅里叶变换等)后，Chirp信号表现为一个冲激函数，其峰值对应的坐标即为接收Chirp信号的初始频率和一次调频率，也就是说，找到峰值及其坐标即可完成载波的快捕。本文采用FRFT对接收信号进行分析。

Chirp信号表达式如下(初始相位设为0):

(1)

式中:A为Chirp信号幅度;f0为Chirp信号初始频率;k为Chirp信号调频率。

其时域图、频率变换图如图1、图2所示。

图1 Chirp信号时域图

分数阶傅里叶变换(FRFT)可以看做传统傅里叶变换(FFT)的分数阶次幂，相当于将信号的时频平面进行一定角度的旋转，设旋转角度α=pπ/2，p称为阶数，旋转后的分析域称为μ域(即分数阶域)，当p=1时，FRFT即为传统意义的FFT,计算公式如下[5]：

(2)

由此推导出Chirp信号f(t)的FRFT计算如下：

(5)

图3 单独Chirp信号投影在阶数轴的曲线

图4 单独Chirp信号FRFT时频聚集三维图

2 基于叠加Chirp信号的载波捕获

基于Chirp信号的上述特性，本文以Chirp信号为参考序列，直接和有用信号进行叠加，Chirp信号以较小的功率直接叠加在有用信号之上，属于一种弱叠加，叠加后的信号经载波调制后通过信道发射。原理框图如图5。

图5 基于叠加Chirp信号的同步方案系统框图

由于Chirp信号是一种恒包络信号，时频变换只会对Chirp信号进行能量汇聚，因此抗干扰和噪声能力强[6]；叠加后的信号经过FRFT后保持能量聚集效应，信号传输过程中所带来的频偏和频偏变化率分别表现为接收端Chirp信号初始频率和调频率的改变量，以分数阶数p为变量对接收信号进行FRFT变换，通过对得到的变换值进行二维搜索找到对应峰值[7]，依据式(5)进行参数估计，将估计得到的值与发送端参数相比较即可算出载波频偏fd和频偏变化率fd_s, 由此来获得频率补偿，完成载波频率捕获。仿真结果如图6、图7所示。

图6 叠加后Chirp信号FRFT投影在阶数轴的曲线

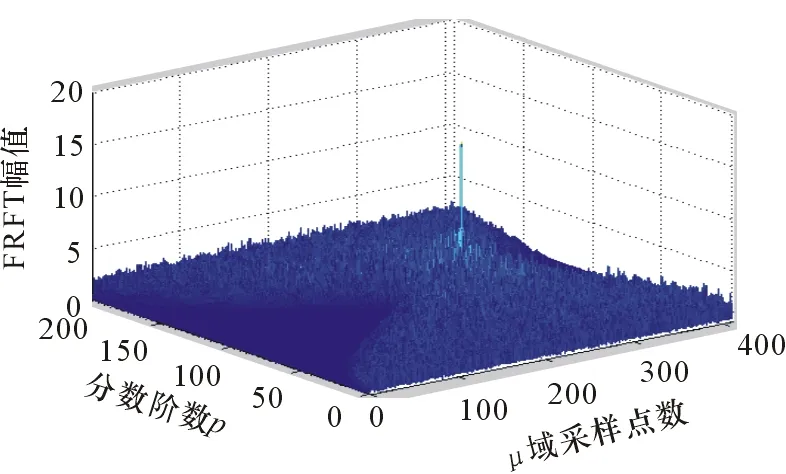
图7 叠加后Chirp信号FRFT时频聚集三维图

仿真信号参数选择：QPSK调制，信息速率10 kbps，Chirp信号与有用信号功率比为1/10，载波频偏fd=2 K，频偏变化率fd_s=200 Hz/s，Chirp信号初始频率f0=500 Hz,调频率k=2 kHz,仿真估计值：fd′=1 996.5，误差△fd=3.5 Hz，fd_s′=202.3 Hz/s，误差△fd_s=2.3 Hz/s；载波频偏fd=20 kHz，频偏变化率fd_s=2 kHz 时，仿真估计值：fd′=19 997.5 Hz，误差△fd=2.5 Hz，fd_s′=2 008.3 Hz/s，误差△fd_s=8.3 Hz/s。

由仿真结果(图6、图7)可看出，叠加后的信号干扰分量能量有所增加，但仍能清晰地得到对应分数阶域的能量聚集效应，完成峰值搜索和参数估计，且估计精度较高。考虑到进行FRFT时，分数阶P若从0～2全部进行变换，计算量较大，当基于合作目标接收，对信道环境及动态范围有一定的先验值可以参考，根据式(5)可以将阶数p的取值缩小到一定范围，从而简化运算量，更快地完成参数估计。

3 结束语

本文以Chirp信号作为参考序列与有用信号直接叠加，通过FRFT完成载波频率参数估计，节省了系统带宽资源和功率资源，参数估计精度较高，通过仿真验证了该方法的可行性，存在的问题是当传输信道环境未知无先验信息可参考时，需在整个μ域(0～2)进行搜索，计算量较大，如何结合应用背景优化改进算法有待进一步研究。

[1] 庞宗山，李小民.基于带极性重复训练序列的OFDM 时频同步[J].郑州大学学报(工学版),2012，33(1):125-128.

[2] 于东海,张海健.基于训练序列的载波频率同步算法的FPGA实现[J].电力系统通信，2006,27(167)：42-44.

[3] Xun Tang,Xuejun Sha.Synchronization using Chirp training sequences based on fractional Fourier transform[A].ISCAA Conference[C].Harbin,2010:1161-1164.

[4] Tao Ran,Deng Bing.Research progress of the fractional Fourier transform in signal processing [J].Science in China,2006,49(1):1-25.

[5] 陶然，齐林.分数阶傅里叶变换及其应用[M].北京:清华大学出版社，2009.

[6] 温容慧，沙学军，张欣宇.一种分数傅里叶域线性调频信号高精度码同步方法[J].西安交通大学学报，2009,43(4)：80-84.

[7] 邓兵,陶然，曲长文.分数阶Fourier域中多分量Chirp信号的遮蔽分析[J].电子学报，2007,35(6)：1094-1097.

Research into Acquisition Method of Carrier Wave Frequency Based on The Superposition Chirp signal

HAN Lei1,2，CHENG Nai-ping1，DING Dan1

(1.The Academy of Equipment,Beijing 101416,China;2.Beijing Space Information Relay and Transmission Technology Research Center,Beijing 100094,China)

Taking Chirp signals as a reference sequence,Chirp signals with weak power are directly superposed on the effective data after moulding and filtering,then the signals are modulated and sent by carrier wave,which saves bandwidth resource and power resource.The constant envelop characteristics of Chirp signal and the time-frequency clustering characteristic of Chirp signal in corresponding fractional step Fourier domain are used to perform fractional Fourier transform (FRFT) to the received signals,the coordinates of peak value is searched,and the parameters of Chirp signal is estimated,thereby the Doppler frequency deviation and its change ratio of carrier wave are acquired,so the carrier wave is acquired and the superposed signal is counteracted.The theory method is feasible through simulation validation.

Chirp signal;fractional Fourier transform;parameter estimation;carrier acquisition

2015-01-20

TN914.42

A

CN32-1413(2015)02-0060-03

10.16426/j.cnki.jcdzdk.2015.02.016