一种改进波形设计的LFMCW雷达多目标检测方法

陆小凯，刘国华

(中国船舶重工集团公司第723研究所，扬州 225001)



一种改进波形设计的LFMCW雷达多目标检测方法

陆小凯，刘国华

(中国船舶重工集团公司第723研究所，扬州 225001)

针对线性调频连续波(LFMCW)雷达中存在的距离-速度耦合及多目标频谱配对问题，提出了一种改进波形设计的方法。该方法通过发射梯形波调制的连续波信号，不仅可以解距离-速度耦合，而且能进行上升段和下降段频谱配对。仿真结果证实了该方法的有效性。

线性调频连续波；梯形调制；频谱配对；多目标检测

0 引 言

线性调频连续波(LFMCW)雷达是一种通过发射频率受线性调制的连续波信号以获取目标参数信息的雷达体制，它具有分辨率高、无测距盲区、低截获和结构简单等一系列优点[1]。近年来，线性调频连续波技术得到了广泛的关注和发展。在军事领域，线性调频连续波雷达在导弹精密末制导、引信、机载导航设备中的应用越来越广泛；在民用领域，其在环境遥感、交通管制等应用中也发挥着越来越重要的作用[2-3]。

目前LFMCW雷达发射波形广泛采用锯齿波调制和对称三角波调制方式。锯齿波调制下的线性调频连续波雷达存在严重的距离-耦合现象[4]，而采用对称三角波调制能够在一定程度上克服上述问题，但在多目标环境中存在调频上升段和下降段频谱配对难的问题。为此，本文提出一种改进波形设计的方法，即采用梯形波调制的连续波作为发射信号。该方法不仅可以解距离-速度耦合，而且可以有效进行频率上升段和下降段频谱配对，适用于多目标环境。

1 LFMCW雷达工作原理

典型的LFMCW雷达系统采用三角波调制的发射波形，其在工作过程中，雷达接收机接收回波信号并与发射信号进行混频得到差频信号，经模数转换采样后作快速傅里叶变换得到频谱信息。接下来对该频谱信息分调频上升段和下降段进行分析处理便可得到目标的参数信息，其工作原理如图1所示。

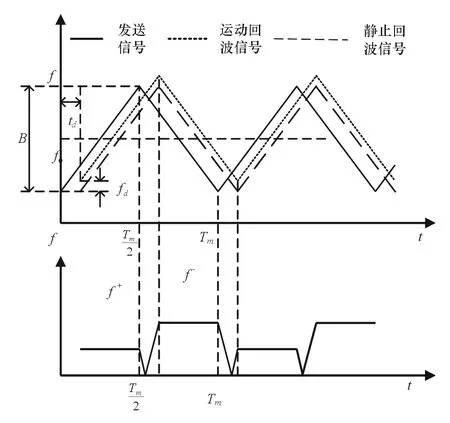
图1 三角波LFMCW雷达原理图

(1)

(2)

由式(2)可推出运动目标的距离和速度，表示为：

(3)

由式(3)可以看出，只要知道目标差频信号在调频上升段和下降段的频谱信息即可算得目标的距离、速度信息。

2 三角波调制下的频谱配对问题

三角波调制的LFMCW雷达系统工作环境中仅存在单个目标时，不用考虑频谱配对。而当目标增多时，无法轻易得到各目标谱线的配对关系，进而无法得到目标的参数。若考虑所有情况，n个目标就存在n2组数据。为简化推导，考虑雷达工作环境中存在3个运动目标的情形。差频信号通过目标检测算法后，其在调频上升段和下降段分别存在3根谱线，分别设为fa1、fa2、fa3和fb1、fb2、fb3。将调频上升段的3个谱线和下降段的3个谱线两两配对，由:

可得到9组距离和速度：

由理论可知上面矩阵中只有对角线的3组是真实目标所对应的参数信息。如果目标数继续增加，按照此法得到的虚假目标的数量将以n2-n倍的速度递增，大大增加了数据冗余度，这样的系统是无法正常工作的。因此，差频信号在经过频域检测后，需要加入频谱配对算法。

3 改进波形设计方法

现有的频谱配对方法主要是频谱特征参数相似法[5]。频谱特征参数相似法利用谱线的面积、相位、功率等特征参数的相似性来进行频谱配对，然而在实际应用中该算法十分复杂且无法检验配对正确与否，可靠性很低。另外，文献[6]提出一种采用变周期调频连续波作为发射波形的方法，可以避开频谱匹配程序，然而变周期调频连续波信号在工程上实现的难度很大。

为了在多目标环境中准确识别出真实目标，并保证测距的精度，本文考虑从波形设计的角度切入，提出一种梯形波调制波形设计的方法，波形图如图2所示。

图2 梯形波LFMCW调制波形

该信号由频率上升段a、恒频段b以及频率下降段c3段信号组成，每段信号的持续时间都为T，调频带宽为B。其工作原理如图3所示。

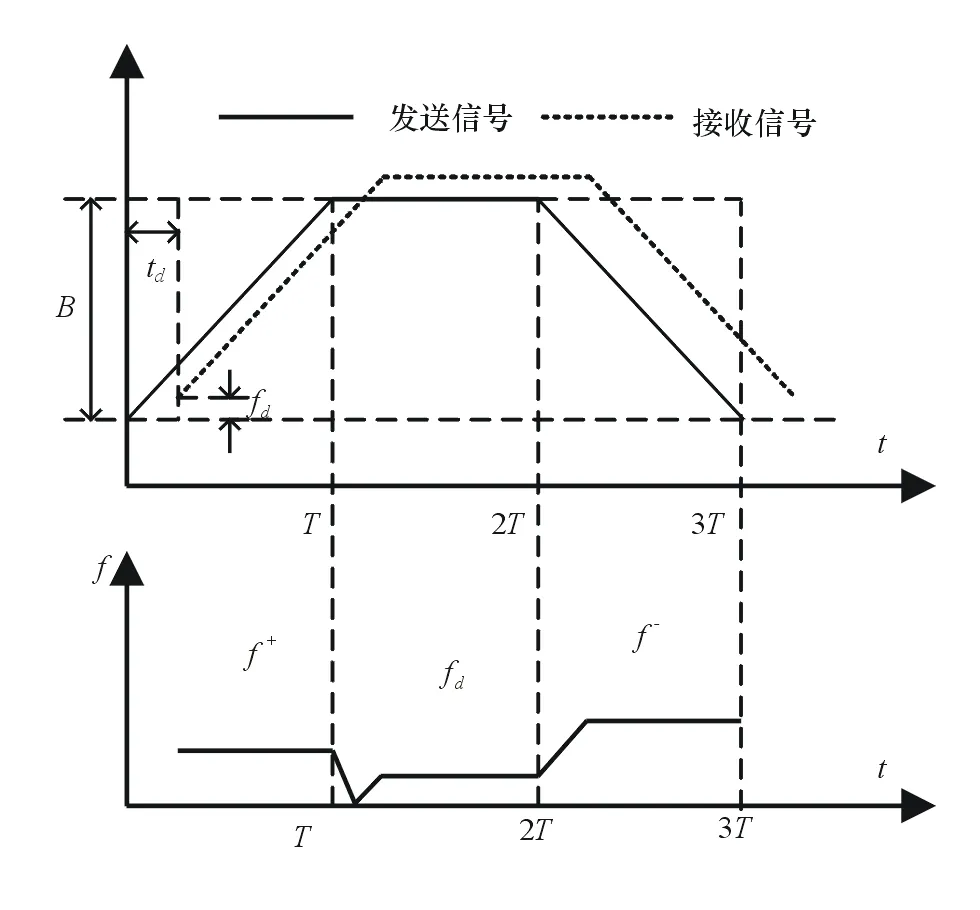
图3 梯形波LFMCW雷达原理图

梯形波LFMCW雷达系统的测距测速原理在频率上升段和下降段时类似于三角调制的情形。为解决频谱配对的问题，在三角波调制的基础上增加一个恒定扫频段，即图2中T～2T的恒频段b，该恒频段产生的差频信号的频率即目标的多普勒频偏fd。在多目标环境中，用fdk表示第k个目标在恒频段对应差频信号的谱线。由式(2)可推出:

(4)

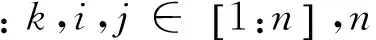
由上式可完成目标k在频率上升段和下降段对应谱线的配对。

4 计算机仿真分析

4.1 波形参数设计

采用梯形波调制时，利用目标的多普勒频率fd来确定目标在调频上升段谱线f+和下降段谱线f-的配对。在慢速目标环境中，fd相对于f+和f-较小，频率分辨率有限，在恒频段检测频谱时容易丢失部分目标的多普勒频率信息，从而导致多目标识别的困难。因此，该波形设计更多适用于快速目标的环境。

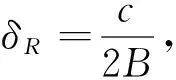
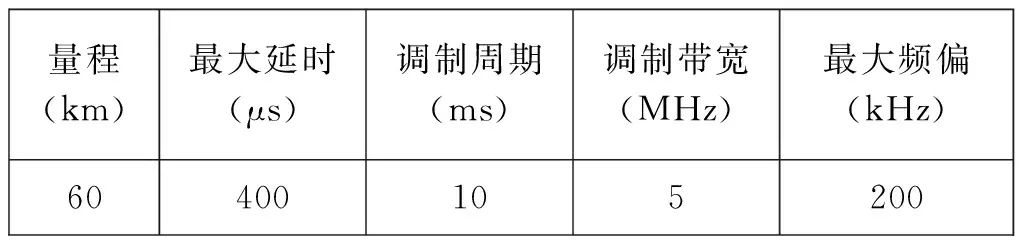
表1 梯形波设计参数

4.2 算法仿真分析

为了验证本文提出的波形设计方法的有效性，下面利用MATLAB仿真平台对该方法进行仿真分析。仿真中，雷达工作参数选择如4.1节，选取4个典型目标，目标参数如表2所示。

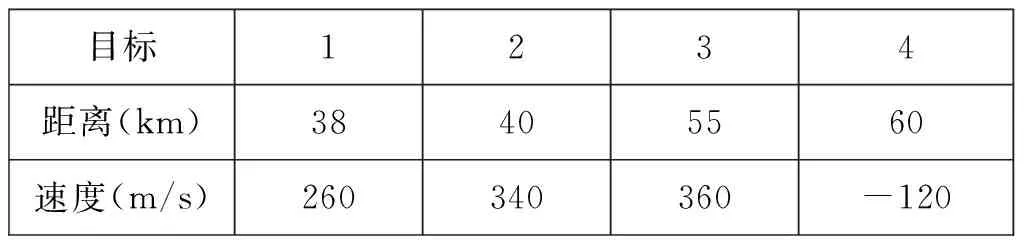
表2 多目标参数

由表2可以看出：目标1和2之间距离相近,但速度不同;目标2和3之间速度相近,但有一定的距离；目标4与其他目标速度相反。假设雷达工作在理想环境，差频信号在调频上升段和下降段经快速傅里叶变换(FFT)后的频谱如图4所示。

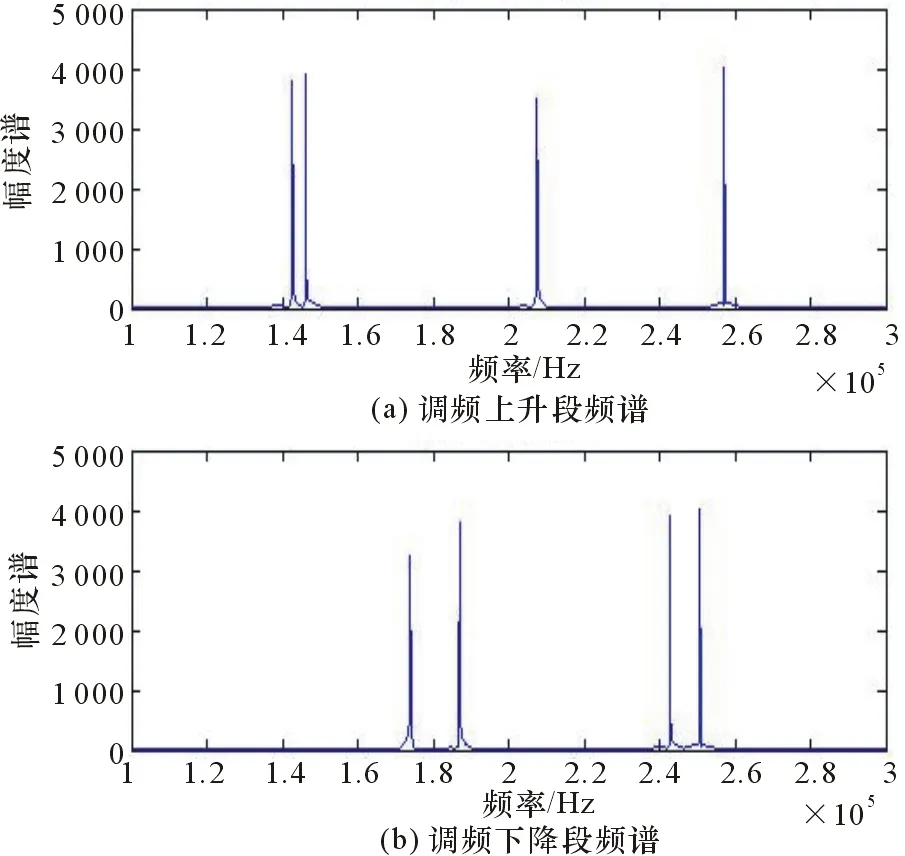
图4 频率上升段和下降段频谱

由图4可以看出，差频信号在调频上升段和下降段分别存在4个谱峰，这正对应着4个目标。依据式(4)将频率上升段和下降段的4根谱线两两配对可得到16个多普勒频率信息，如图5所示。

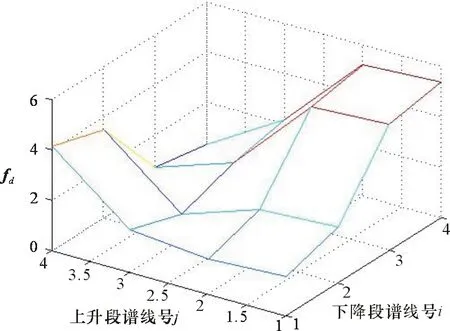
图5 匹配后的多普勒频率三维图

对图5进行峰值搜索可得到16个多普勒频率构成的矩阵fd(4×4)：

再对恒频段的差频信号作快速傅里叶变换(FFT)可得其频谱如图6所示。

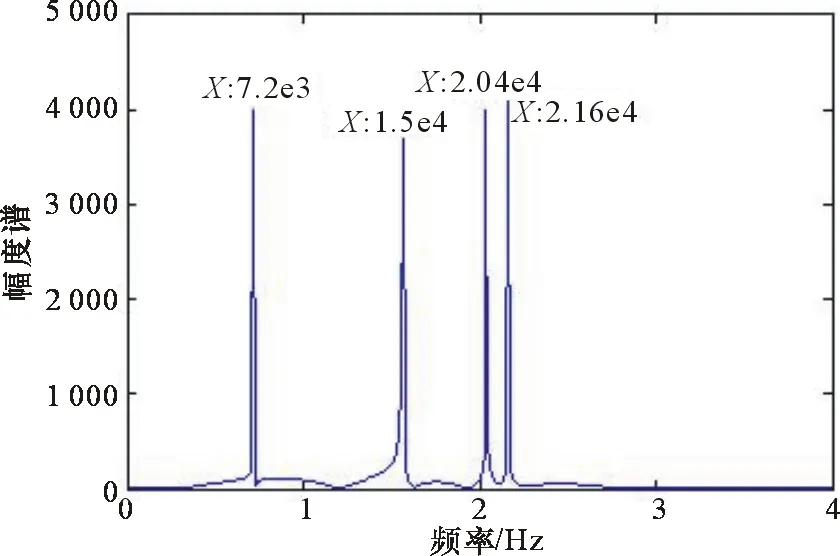
图6 恒频段频谱

依据理论可知，图6中4根谱线即为4个运动目标对应的多普勒频率，图中已标注出它们的频率值，分别为7.2e3、1.56e4、2.04e4、2.16e4。再将它们与之前计算得到的矩阵fd(4×4)比对可发现，矩阵中(1,1)、(2,2)、(3,4)、(4,3)位置上的值与恒频段得到的目标多普勒频率相同，进而可推出调频上升段中1,2,3,4号谱线与下降段中1,2,4,3号谱线是相互匹配的。

5 结束语

线性调频连续波雷达多目标检测问题一直是阻碍其得到广泛应用的难题之一。本文考虑从波形设计的角度切入，提出一种梯形波调制波形设计的方法。

该方法利用频率上升段和下降段解距离-速度耦合，利用恒频段进行目标谱线配对。

仿真结果证实了该方法可在目标谱线正确检测后有效分辨出不同目标，对工程设计方案有一定的指导意义。

[1] 丁鹭飞,耿富录.雷达原理[M].第3版.西安:西安电子科技大学出版社,2002.

[2]StoveAG.LinearFMCWradartechnique[J].RadarandSignalProcessing,IEEProceeding-F,1992,139(5):343-350.

[3]VesuovoR.Patternsynthesiswithnullconstraintsforcirculararraysofequallyspacedisotropicelements[J].MicowaveAntennasPropagation,IEEProceedings，1996,143(2):103- 106.

[4] 杨建宇,凌太兵,贺峻.LFMCW雷达运动目标检测与距离速度去耦合[J].电子与信息学报,2004,26(2):169-173.

[5] 史林,张琳.调频连续波雷达频谱配对信号处理方法[J].西安电子科技大学学报(自然科学版),2003,30(4):534-538.

[6] 徐涛,金昶明,孙晓伟,夏冠群.一种采用变周期调频连续波雷达的多目标识别方法[J].电子学报,2002,30(6):861-863.

A Method of Improving Waveform Design for LFMCW Radar Multi-target Detection

LU Xiao-kai,LIU Guo-hua

(The 723 Institute of CSIC，Yangzhou 225001)

Aiming at the problems of range-velocity coupling and multi-target spectrum matching in linear frequency modulation continuous wave (LFMCW) radar,this paper proposes a method to improve waveform design.By transmitting continuous wave signal modulated by trapezoidal wave,not only the range-velocity coupling can be solved,but also the frequency spectrums of rising segment and falling segment can be matched.Simulation results validate the validity of the method.

linear frequency modulation continuous wave;trapezoidal modulation;spectrum matching;multi-target detection

2014-10-08

TN958

A

CN32-1413(2015)02-0033-04

10.16426/j.cnki.jcdzdk.2015.02.010