DCT变换与DNA运算相结合的图像压缩加密算法

徐光宪，徐山强，郭晓娟，华一阳

(辽宁工程技术大学 电子与信息工程学院，葫芦岛 125105)

DCT变换与DNA运算相结合的图像压缩加密算法

徐光宪，徐山强，郭晓娟，华一阳

(辽宁工程技术大学 电子与信息工程学院，葫芦岛 125105)

摘要：为了解决图像加密后数据量大、传输速率慢的问题，采用了离散余弦变换(DCT)与脱氧核糖核酸(DNA)运算相结合的图像压缩加密方法。首先采用DCT对原始图像进行压缩；再进行DNA编码；最后根据DNA运算的思想，通过Chen混沌系统对原始图像执行DNA加法运算，成功得到了加密图像。结果表明，该算法不仅有效地提高图像传输速度、减少存储空间,同时加密效果好、安全性高。

关键词：图像处理；图像压缩加密；离散余弦变换；脱氧核糖核酸加法运算；Chen混沌系统

E-mail：5261009@qq.com

引言

信息化社会的飞速发展使计算机多媒体技术得到了广泛应用。使得图像信息相关技术的安全性成为一项亟待解决的问题[1-2]。数字图像比传统文字信息的信息量大，与有线网络的传输能力相制约，因此，图像的压缩与传输是实际应用研究方向的热点。

针对图像加密后的存储以及快速传输，许多研究人员对图像压缩与加密相融合的算法进行了研究。2008年PENG等人[3]提出基于混沌序列的压缩图像加密算法，具有较好的加密效果。2011年GU等人[4]提出基于混沌映射的图像Contourlet编码加密算法，提高了安全性，但这种算法对原始图像不敏感。2012年YANG等人[5]提出了一种基于多级树集合分裂(set partitioning in hierarchical trees,SPIHT)的图像加密与压缩关联算法，虽加密效果好，但传输速率慢。2013年LIN等人[6]提出了一种基于混沌的图像压缩加密算法，虽然提高了传输速率，但安全性需要进一步提高。

基于上述现状，作者先利用离散余弦变换(discrete cosine transform，DCT)压缩及Chen混沌系统置乱图像后，再用脱氧核糖核酸(deoxyribonucleic acid，DNA)序列加法运算结合超混沌映射来加密图像信息。本文中的算法不仅具有传输速度快、占用空间小的特点，同时亦可使图像加密效果得到显著提高，充分保证图像加密后安全性高。仿真实验分析表明，相对于其它图像压缩加密算法而言，在面对穷举和差分攻击手段时，具有良好的鲁棒性。

1理论知识

1.1　DCT变换

DCT是一种实数域的余弦函数[7]。在实验中，进行DCT变换之前，先把图像分成8pixel×8pixel的子块，每一单独子块进行2维DCT变换，其2维DCT变换定义如下：

(1)

式中，f(i,j)表示图像矩阵的像素值，i和j表示图像矩阵的坐标位置；F(μ,ν)表示DCT变换后矩阵的系数，μ和ν表示矩阵的坐标位置。

2维DCT逆变换定义为：

(2)

其中，

(3)

对数字图像而言，大多数图像经过DCT变换后矩阵的系数值非常趋近于0，假如舍弃这些趋近于0的系数值，在恢复原始图像时，不会影响图像画面的质量。因此，采用DCT 变换对图像进行压缩可以减少存储空间的占用。在DCT压缩编码时，将一幅数字图像分成8pixel×8pixel块进行压缩。

1.2　超混沌Chen系统

超混沌Chen系统方程式描述如下[8]：

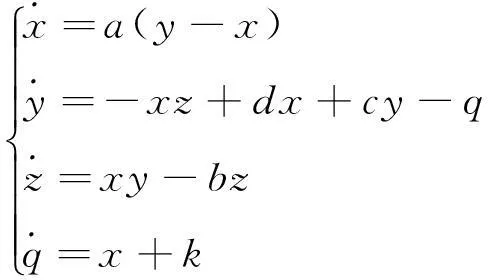
(4)

式中，a，b，c，d和k是系统的控制参量。当a=36，b=3，c=28，d=16和-0.7≤k≤0.7时，系统为超混沌状态并产生4个混沌序列。选取参量a=36，b=3，c=28，d=16和k=0.2，此时系统的Lyapunov指数为λ1=1.552，λ2=0.023，λ3=0，λ4=-12.573[9]。

1.3　DNA密码

1.3.1图像的DNA编码和解码一个DNA[10]链由4个不同的基本核苷酸基因组成，即腺嘌呤(A)、胸腺

Table1EightschemesforencodinganddecodingmapruleofDNAsequence

rule12345678A0000010110101111C1001110011001001G0110001100110110T1111101001010000

嘧啶(T)、胞嘧啶(C)和鸟嘌呤(G)，这4种核苷酸能够结合在一起形成一条长序列，且A与T配对，C与G配对。通过规定A，C，G，T分别编码为00，01，10，11，这样的编码方案有24种，但只有8种编码方案满足Watson-Crick规则，如表1所示。

1.3.2DNA序列的加减代数运算DNA序列加法和减法运算是源于在传统二进制中加法和减法[11]，如表2和表3所示。

Table 2　Addition operation of DNA sequence

Table 3　Subtraction operation of DNA sequence

2算法实现方案设计

本文中提出的加密算法，定义DNA序列由4个碱基可以表示图像的1个灰度值，方案包括4个部分：(1)原始图像用DCT变换进行分块压缩处理；(2)DNA矩阵排列替换和混沌序列置乱；(3)在Chen混沌系统下进行DNA序列运算和加法运算以改变像素值；(4)通过上面的操作应用规则解码图像，即得加密图。

根据加密方案流程图(见图1)，详细的加密过程如下所示：

(1)导入一幅灰度图像作为原始图像，表示为A(m，n)，其中m，n分别表示图像的行和列，将图像分成8piexl×8piexl块。

(2)将每个像素块进行DCT变换，由(1)式可以得到变换后的DCT系数矩阵B。

(3)根据规则7对矩阵B进行DNA编码，如表1所示。得到编码矩阵B1。

(4)通过Chen超混沌系统产生4个混沌序列，分别为s1，s2，s3，s4。

(5)利用索引函数对混沌序列s1进行操作，公式

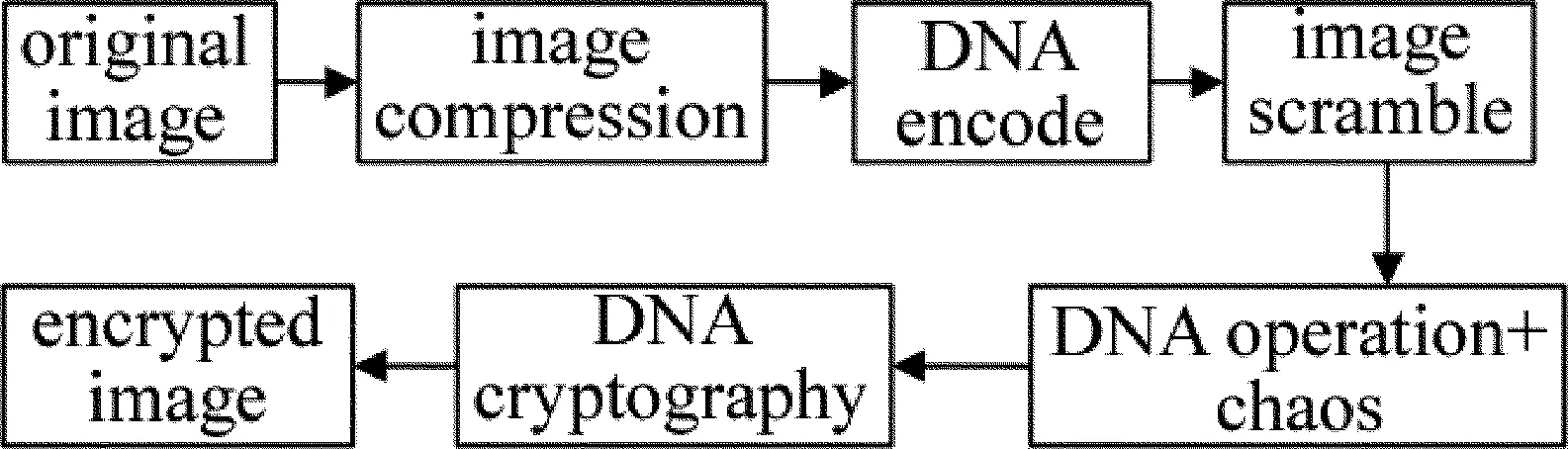
Fig.1　Block diagram for the image compression encryption algorithm

如下：

(5)

(5)式表示排序的索引函数，fs1是把s1升序排列后的新序列，ls1是s1的索引值。s2，s3，s4与s1一样。

(6)选择(fs1,fs3)的组合去置乱矩阵B1，公式如下：

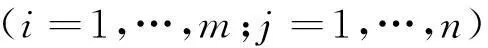
(6)

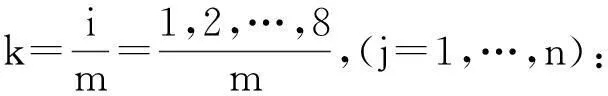
(7)

(8)利用第3个DNA解码规则，根据表1对矩阵B1进行解码，将得到两个二进制矩阵P，P就是加密图像。

解密过程是加密的逆过程。按照上述算法的相反操作进行解密图像，其中加法运算在第(7)步替换为减法运算，其它步骤保持不变。

3仿真结果及分析

对本文中提出的加密方案设计，输入一幅256pixel×256pixel的灰度图像baboo作为导入图像，图像大小为65kbyte，正确解密图像大小为20.7kbyte，原图像的大小是解密图的3倍多，减小了占用空间，这样就加快了传输速度。用MATLAB做仿真实验，设各个参量分别为k=0.3,s1(1)=0.2,s2(1)=-0.4,s3(1)=1.3,s4(1)=1。灰度图像加密前后变化如图2所示，图2a为原始图像，图2b为压缩加密图像，图2c为原始图像的直方图，图2d为压缩加密图像的直方图，横纵坐标表示在(0,255)的像素分布情况。由此表明本文中提出的算法可以得到良好的加密效果。

3.1　密钥空间分析

本文中的算法将Chen超混沌系统的初始值作为密钥，因此共有5个密钥，如果计算机精确到10-14，密钥的空间大小为1070，又因为DNA编码规则共有8种，任选一种编码规则的密钥空间约为1070，因而说明密钥空间足够大，可以抵抗穷举攻击。

3.2　执行效率分析

本文中算法对一幅256pixel×256pixel的8位baboo灰度图像进行压缩加密，平均耗时约0.0917s。将参考文献[4]中的算法在相同的计算机环境下进行图像加密操作，则平均时耗约为0.1851s。由此可见，本文中提出的图像压缩加密算法的执行效率大约是参考文献[4]中加密算法的2倍。

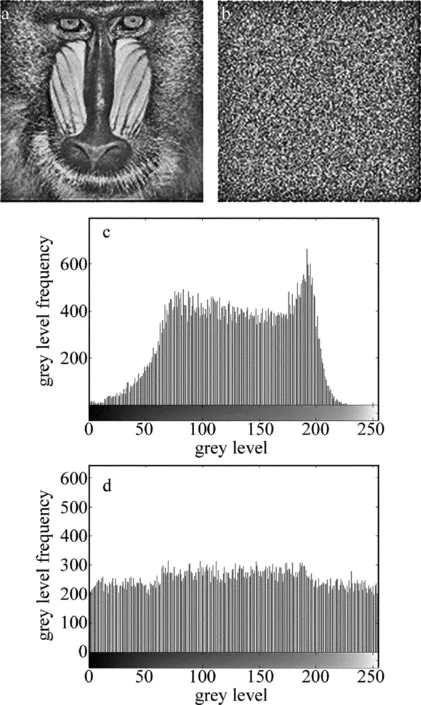
Fig.2　Experimental result of encrypted algorithma—original image　b—image of compression and encryption　c—gray histogram of original image　d—gray histogram of compression and encryption

3.3　敏感性分析

Chen超混沌系统都是对系统参量和初始值非常敏感的。这意味着，如果初始值有轻微的改变所解密的图像将与原始图像没有联系。如图3所示，在解密过程中，密钥s1(1)增加0.0000001去解密图像，图3a、图3b是解密图像，图3c、图3d是对应的直方图。其它参量的灵敏度与s1(1)一样。基于上述理论，该算法是密钥敏感，表明它具有抗穷举攻击的能力。

3.4　抗噪声性能分析

每幅灰度图像在传输过程中，都会受到噪声信号的干扰。抗噪声性能是通过给加密图像加入20%的椒盐噪声和均方差为20的高斯噪声，然后得到解密图。为了验证本文中压缩加密算法的抗噪声性能，对加密图像加入20%的椒盐噪声，解密的图像如图4a所示；对加密图像加均方差为20的高斯噪声，解密的图像如图4b所示。从图中可以看到，解密图受到了影响，可以看到解密图部分像素点无法恢复，但解密后的图像仍可以反映出原始图像的轮廓。因此说明该算法的抗噪声攻击性能较好。

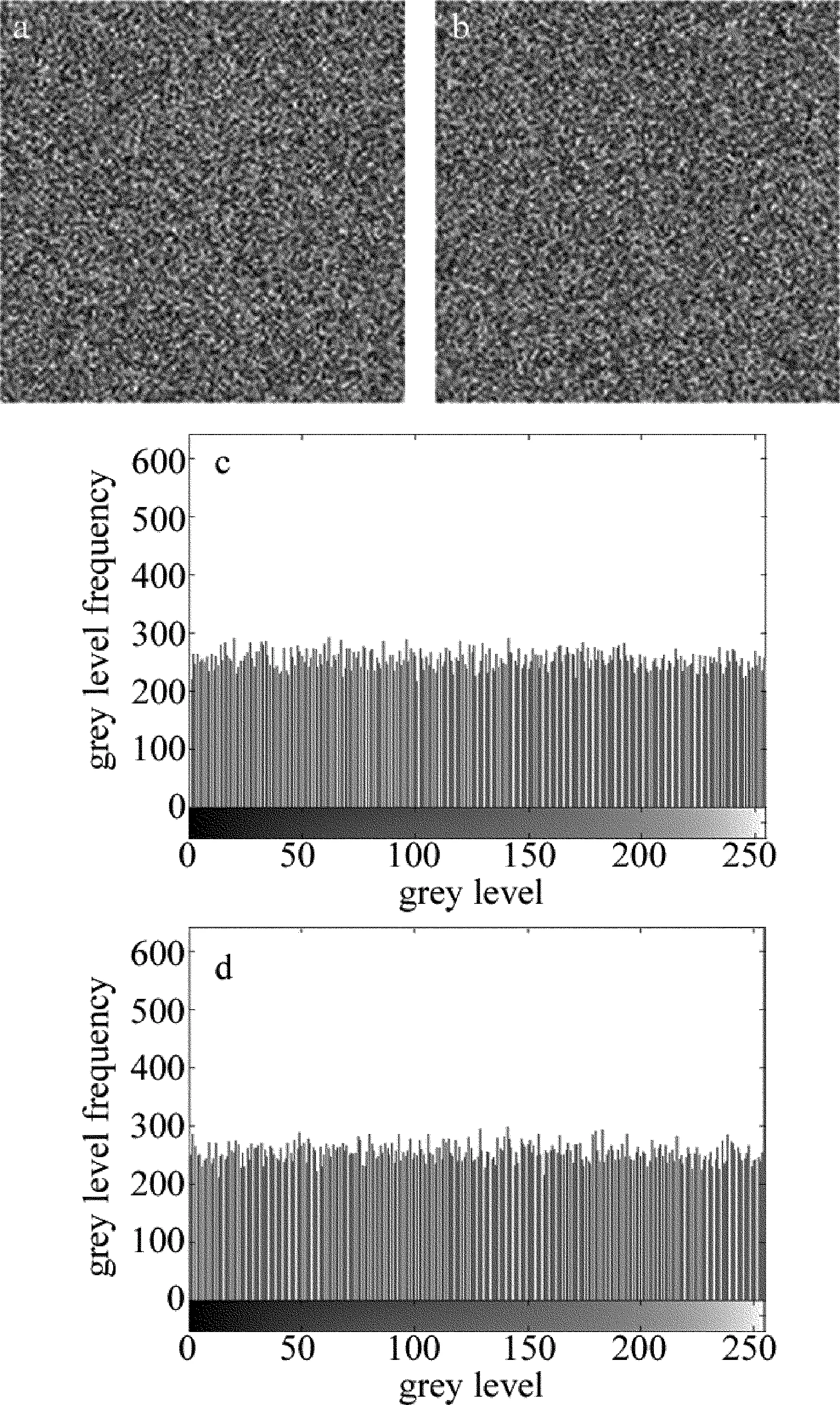
Fig.3　Sensitivity analysis of incorrectly secret key

a—decryptionmapofkeys1(1)=0.2000001b—decryptionmapofkeys3(1)=1.3000001c—graphhistogramofdecryptionmapofkeys1(1)=0.2000001d—graphhistogramofdecryptionmapofkeys3(1)=1.3000001

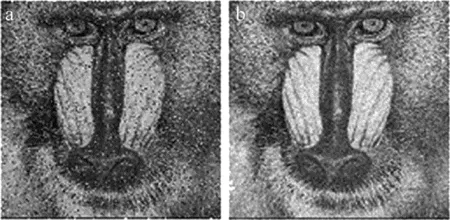
Fig.4　Decrypted image of noise attacks

a—decryptionmapof20%saltandpeppernoiseb—decryptionmapofGaussiannoisewithmeanvariance20

3.5　相邻像素相关性分析

随机选取明文和密文中的相邻3000对像素，图5a表示原始图像垂直方向的相邻像素，图5b表示压缩加密后图像垂直方向的相邻像素；从图中可以看到，图像加密前后的相邻像素差别很大，图像加密前像素集中，图像压缩加密后像素分布均匀，可以抵御统计攻击。

3.6　明文敏感性分析

差分攻击是原图像的一个微小改变能引起加密图像的巨大变化，攻击者能获得原始图像与加密图像之a—theoriginalimageofadjacentpixelsb—theencryptedimageofadjacentpixels

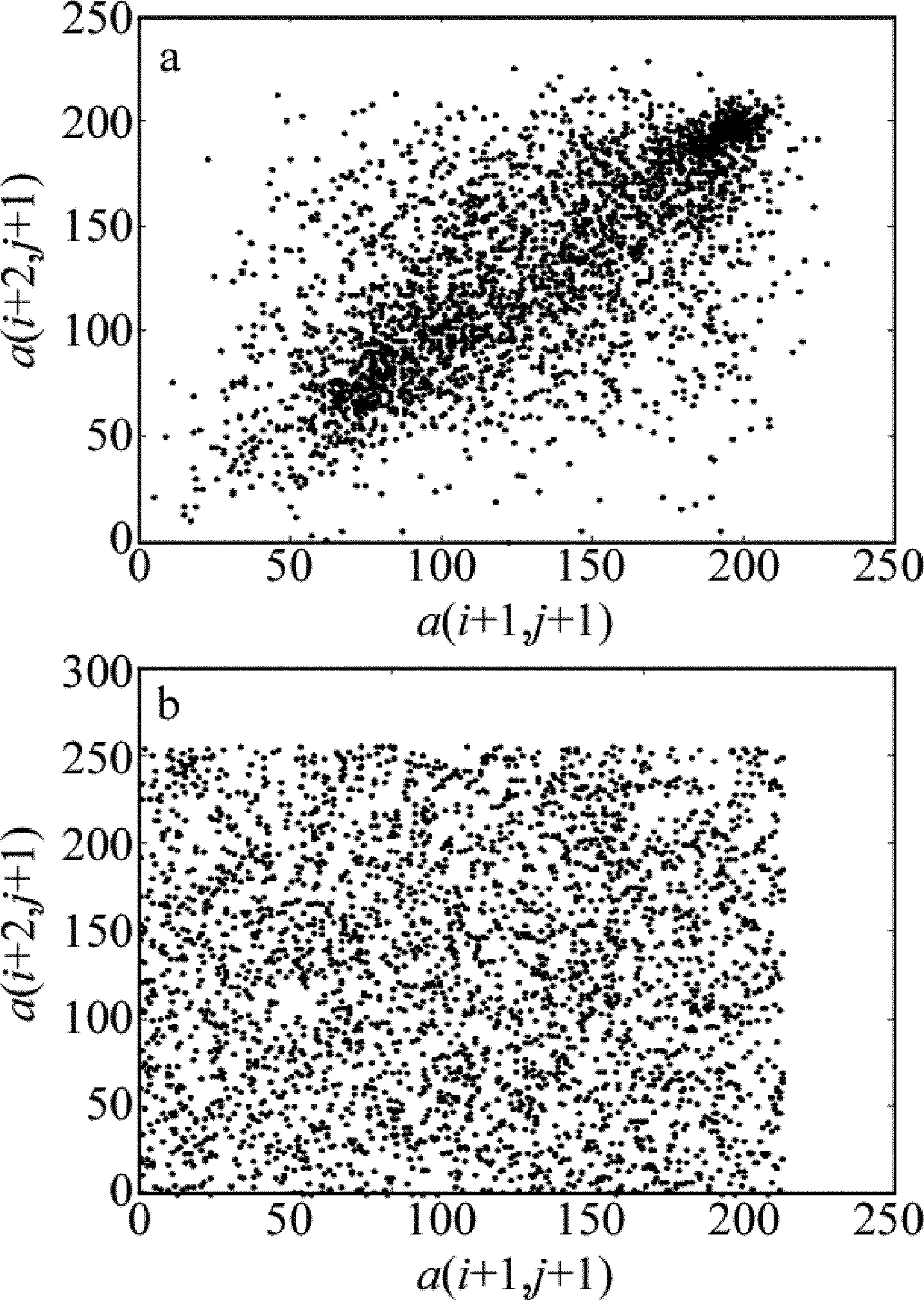
Fig.5　Correlation analysis of adjacent pixels

间的联系。通过像素改变率 (thenumberofpixelchangerate,NPCR)与平均像素改变密度(theunifiedaveragechangingintensity,UACI)来衡量[12]。公式如下：

(8)

(9)

式中，m与n分别表示图像的行和列，C1与C2分别为仅改变原图像的一个像素值而得到的不同加密图，C1(i,j)与C2(i,j)表示在(i,j)坐标上的像素值。

ENPCR和FUACI的计算值如表4所示(ENPCR和FUACI分别表示加密图像的像素改变率和平均像素改变密度)。可以了解到只要原图像发生微小的改变，会使加密图像接近100%的NPCR发生变化，加密后的图像平均变化在30%(FUACI)以上。同时也说明明文图像的信息很好地扩散到了密文图像中，相比参考文献[4]和参考文献[6]中提出的算法具有很好的明文敏感性，对差分攻击有很好的鲁棒性。

Table 4　Sensitivity analysis of plain text and comparison

4结论

提出了一种DCT变换与DNA运算相结合的图像压缩加密算法，通过DCT变换压缩数字图像，接着进行DNA编码，然后由DNA序列加法运算来改变原始图像的像素值。通过实验结果表明，本文中的算法具有良好的加密效果，密钥空间大和密钥敏感性强。此外，加密效率高，并且能够抵御举攻击和噪声攻击以及差分攻击。

参考文献

[1]ZHANG H Z, YAO M, LEI P,etal. Research of image processing method of far-field laser spots[J]. Laser Technology, 2013, 37(4):460-463(in Chinese).

[2]LIN R, LIU Q N, ZHANG C L. A new fast algorithm for gyrator transform[J]. Laser Technology, 2012, 36(1):50-53(in Chinese).

[3]PENG C, LIU L. Encryption algorithm for compressed images based on chaotic sequences[J]. Computer Engineering, 2008, 34(20):177-179(in Chinese).

[4]GU G S, LIU F C. Contourlet domain image encryption based on chaos mapping[J]. Journal of Computer Applications, 2011, 31(3):771-773(in Chinese).

[5]YANG H Q, LIAO X F, WONG K W,etal. SPIHT-based joint image compression and encryption[J]. Acta Physica Sinica, 2012, 61(4):40505(in Chinese).

[6]LIN C, WANG J P, MA W G,etal. Study on chaotic encryption algorithm for images after compression[J]. Microelectronics & Computer, 2013, 30(3):5-7(in Chinese).

[7]CONG S, PU Y K, WANG J N. DCT based image compression algorithm and application[J]. Computer Engineering and Applications, 2010, 46(18):160-163(in Chinese).

[8]LI L, WANG W N, LI J J. Security improvement for image encryption algorithm based on hyper-chaos system[J]. Application Research of Computers, 2011, 28(11):4335-4337(in Chinese).

[9]LU H B, SUN Y. Image encryption scheme based on novel hyperchaotic system[J].Computer Science,2011,38(6):149-152(in Chinese).

[10]RAHIMOV H, BABAEI M, HASSANABADI H .Improving middle square method RNG using chaotic map[J]. Applied Mathematics, 2011, 2(4):137-141.

[11]SADEG S, GOUGACHE M, MANSOURI N,etal. An encryption algorithm inspired from DNA[C]// 2010 International Conference on Machine and Web Intelligence (ICMWI).New York, USA:IEEE, 2010:344-349.

[12]WANG Y, WONG K W, LIAO X,etal. A new chaos-based fast image encryption algorithm[J]. Applied Soft Computing, 2011, 11(1):514-522.

Image compression-encryption algorithm combined

DCT transform with DNA operation

XUGuangxian,XUShanqiang,GUOXiaojuan，HUAYiyang

(School of Electronics and Information Engineering, Liaoning Technical University, Huludao 125105, China)

Abstract：In order to solve the problems of huge amount of data and slow transmission speed after image encryption, a new image compression encryption algorithm combined discrete cosine transform (DCT) with deoxyribonucleic acid (DNA) operation was presented. At first, the original image was compressed by means of DCT and encoded according to DNA sequence. Finally, based on DNA operation, DNA addition operation was implemented to the original image by Chen chaotic system and an encrypted image was obtained. Simulation results show that the algorithm not only improves the speed of image transmission and reduces the storage space, but also has good encryption effect and high security.

Key words:image processing; image compression encryption; discrete cosine transform; deoxyribonucleic acid addition operation; Chen chaotic system

收稿日期：2014-09-09；收到修改稿日期：2014-10-13

作者简介：徐光宪(1977-)，男，博士，教授，主要研究方向为网络编码和信息处理。

基金项目：辽宁省高等学校杰出青年学者成长计划资助项目(LJQ2012029)

中图分类号：TP309.7

文献标志码：A

doi:10.7510/jgjs.issn.1001-3806.2015.06.016

文章编号：1001-3806(2015)06-0806-05