面向海洋监测的传感数据可用性评价技术
刘红蕾,张峰,谷峪,鲍玉斌,李芳芳,于戈
(1.东北大学 计算机软件与理论研究所,辽宁,沈阳 110819;2.国家海洋信息中心,天津 300171)
随着技术的进步,传感器硬件设备的感知精度、自适应能力均得到了大幅提升,无线传感器网络的应用范畴越来越广阔。无线传感器网络不需要线缆等基础设施 (Akyildiz et al,2002;任丰源等,2003) 较好地克服了人工方式现场工作量大和无法保证数据实时有效性的缺点,非常适合针对海洋等复杂环境的监测任务。但由于传感节点本身的能量限制和位置分布并不均匀,目标区域内不同位置的被感知和估算的环境信息在可用性方面差异较大;此外,节点的位置不可避免地会受到海洋复杂环境的影响而改变,从而导致目标区域感知数据可用性的动态变化。综上,面向海洋应用的特点,建立高效的时空模型对感知数据可用性进行评价,从而获取高质量的可用信息成为亟待解决的问题(郑琳等,2014)。针对上述挑战,本文充分分析了传感器节点的数据获取模型,能量消耗模型,还进一步针对海水的流动性,引入改进的Leeway 漂流模型,对随机部署在海洋表面的传感器节点的运动状态进行建模,使其能够更加真实地反映海洋环境。进一步从数据的可靠性和时效性两个方面对数据的可用性进行评价,探索了在保证数据可用性前提下的高质量数据源选择方法及航行路线评价方法,并通过仿真实验展示了采用的模型对上述应用的有效支持。
1 相关模型
为了通过无线传感器网络获取海洋数据信息,本文引入了相适宜的传感器节点的感知模型和能量消耗模型。同时,考虑到WSN(Wireless Sensor Network) 在复杂的海洋环境中的移动性,引入了海洋搜索中常用的改进的Leeway 模型来对传感器节点的运动状态进行建模。接下来,本节就将介绍这3 个模型,为传感数据可用性评价技术的提出奠定基础。
1.1 传感器节点的感知模型
1.1.1 概率感知模型
在传感器网络的研究中,主要有两类感知模型(Yao et al, 2009):一种是确定性感知模型(deterministic sensing model),如Boolean sensing model;一种是概率感知模型,包括Shadow-fading sensing model (Patwari et al, 2003) , Elfes sensing model (Savvide et al, 2001) 等。Boolean sensing model 是一种较为简单的感知模型,在传感器网络的研究中应用普遍。相对而言,概率感知模型能够更为准确地表示出节点的感知特性。本文所采用的便是概率模型中的一种,即Elfes sensing model。
根据Elfes sensing model 的描述,一个节点能够探测到距它的距离为d 的事件的概率为:

其中,R1为传感器节点的感知范围。参数λ和γ 的值由节点的物理特性决定。Rmax是节点的最大感知范围。这是一种较为普遍的感知模型,因为当R1= Rmax时,该模型即变为Boolean sensing model。Yao 等(2009) 将这个模型进行了简化:
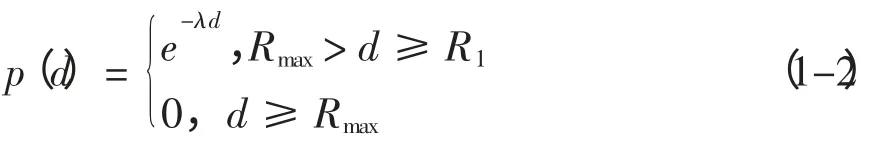
在本文之后的研究和实验中,采用的便是这种简化的Elfes sensing model。
1.1.2 联合探测概率
在传感器网络中,一个目标往往可以被多个传感器节点同时感知,故而对该目标的探测是这些传感器节点协同作用的结果。因此,在对感知目标的有效探测概率进行计算时应采用联合探测概率。
假设S= {s1,s2,…,sn} 为所有可以对点Pj进行感知的传感器节点集合,则点Pj可被传感器网络探测到的概率为:

其中,p(i,j)为传感器节点Si对点Pj的探测概率。根据上式,可对监测区域的探测概率分布进行计算。
1.2 能量消耗模型
1.2.1 相关假设
对研究的传感器网络做如下假设:
a) 假设各节点的位置已知,因为现有的无线传感器网络节点定位技术已十分成熟(Jain et al,2006;Erdun et al,2009;Wang et al,2007)。
b) 假设所有的传感器节点是同构的,具有相同的工作参数和初始能量。
c) 假设每个节点在单位时间内均产生和发送l比特数据。为了便于研究,假设网络采用单跳方式传输数据,即每个节点直接向汇聚节点发送数据。
d) 假设汇聚节点的能量足够多,不会在网络工作时因能量耗尽而死亡。
网络以周期性的方式工作,一个节点在一个周期内完成对被监测对象的数据采集,并将所获得的数据包发往基站。
1.2.2 能耗模型
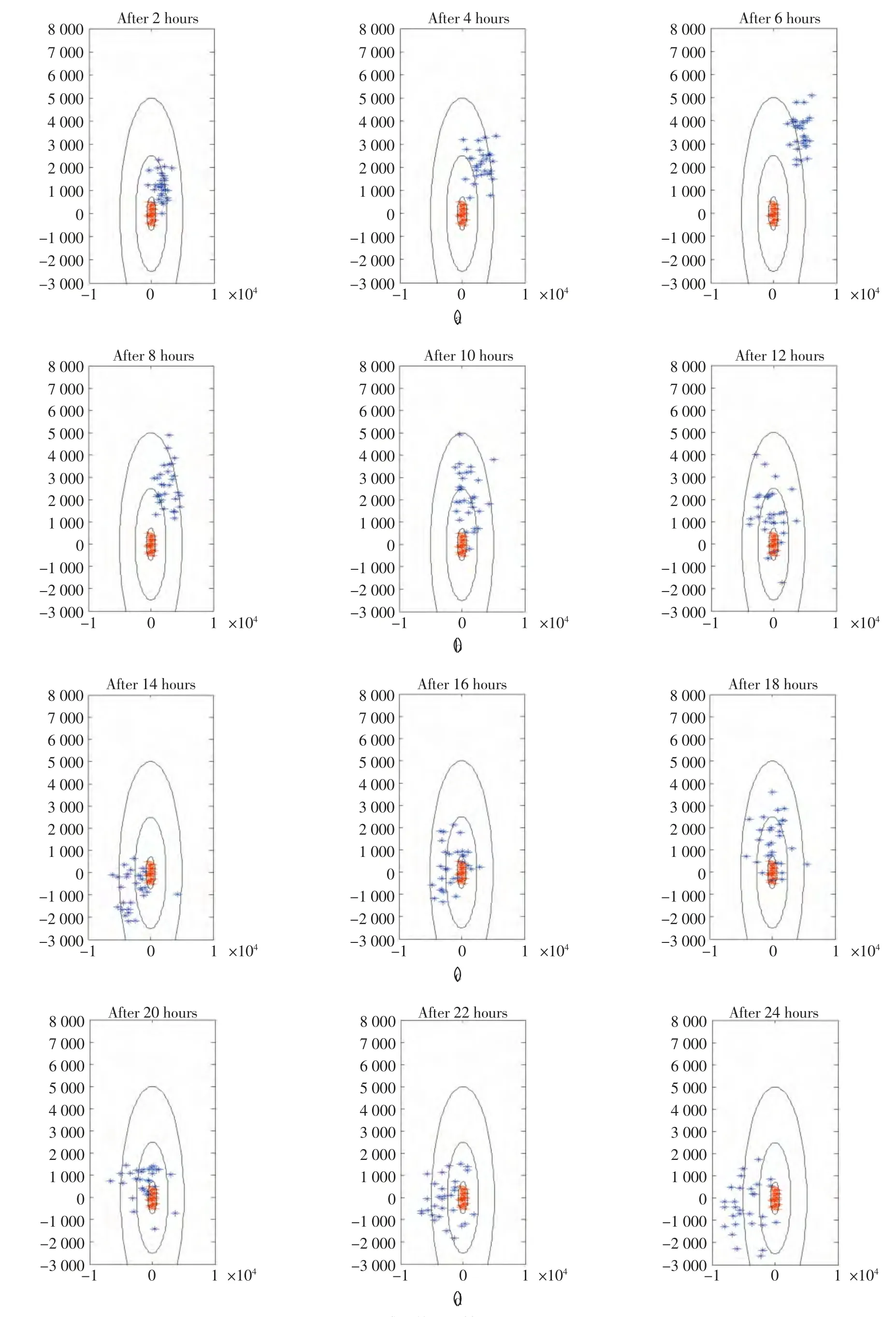
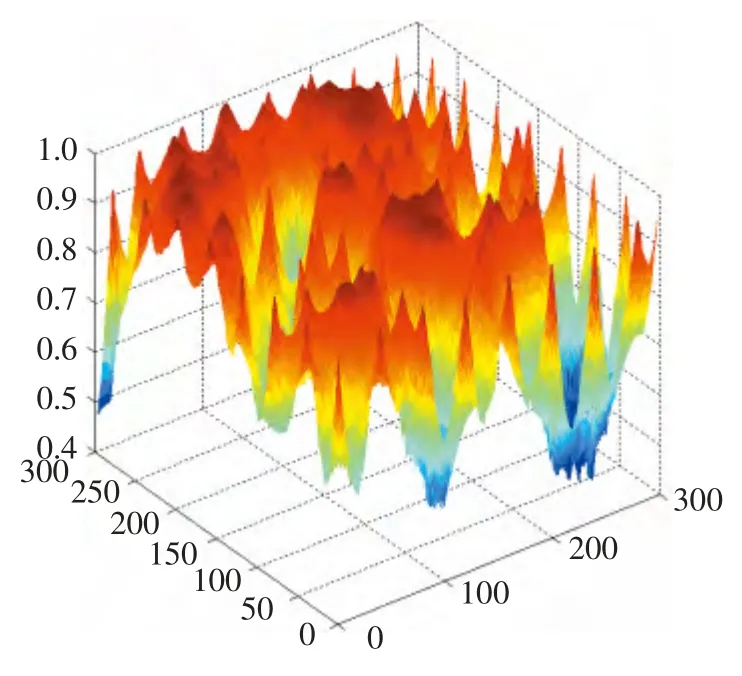
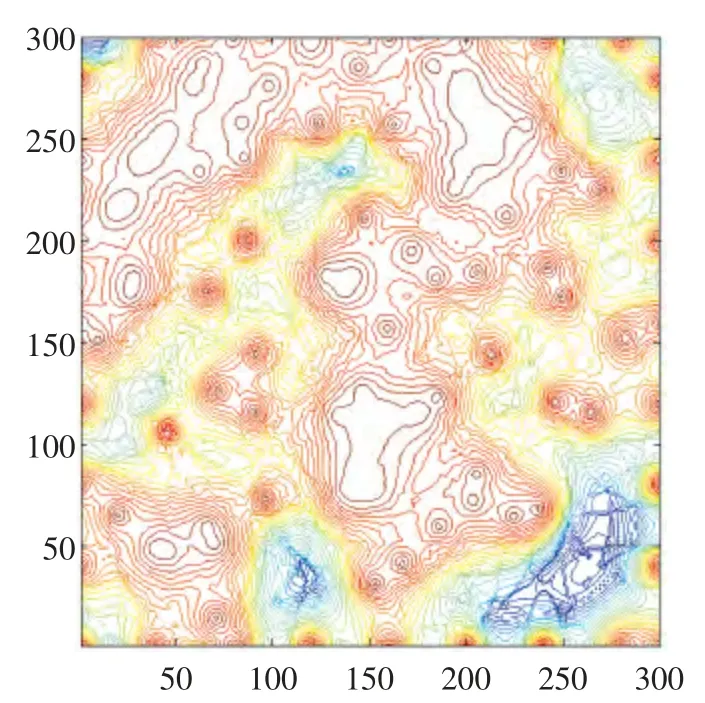
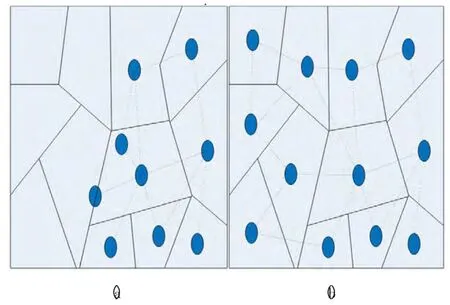
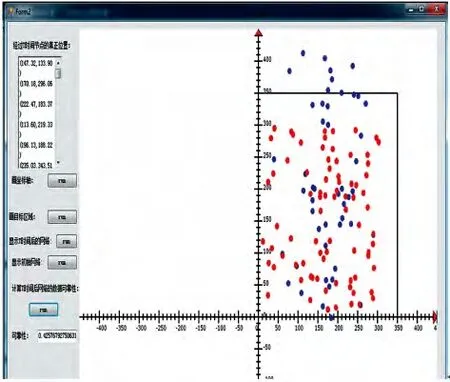
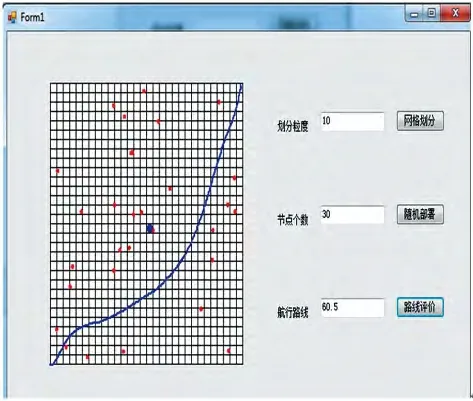
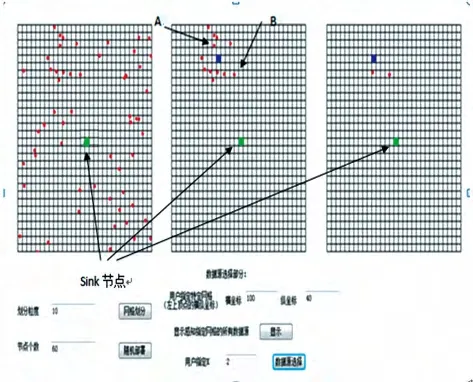
采用Wang 等(2001) 提出的模型来计算节点的能量消耗,该模型也是目前多数有关网络能耗问题的研究所采用的。该模型根据发送方和接收方的距离d,设定一个阈值d0,近距离传输(d 式中:Eelec表示发射装置和接收电路每发送或接收单位比特的耗能。ETx(l,d)是发送端向距离d 发送l比特的数据所消耗的能量。ERx(l)是接收端接受l比特数据所消耗的能量。而放大器能量εfs·d2和εfs·d4由到接收器的距离和能够接受的比特误差率决定。对于本文中的实验,通信能量参数设定如表1 所示。 表1 能耗模型参数 进一步地,对到汇聚节点距离不同的传感器节点的工作寿命进行分析。假设传感器节点的初始能量为E0,网络的工作周期为T,则节点Sk的工作寿命即传感器节点的持续时间Tlast(Sk)计算公式如下: 区别于陆地,无线传感器网络的节点部署及网络性能均会受到海面环境的影响。从而传感器网络获取的感知数据的可用性也会随着逐渐改变。因此本文引入了刘磊(2012) 中的改进的Leeway 漂流模型,对随机部署在海洋表面的传感器节点运动状态进行建模,从而能更准确地建立传感数据的可用性的评估模型,反映真实的海洋环境状况。 1.3.1 改进的Leeway 模型介绍 通过查阅可知,传感器节点的运动方程为: 这里(X0,Y0)为节点初始位置, X(Δt)(Y(Δt ))为经过Δt 时间后的位置,vx,vy为速度在x和y 方向上的分量。θ=2π[R]01表示水平扩散方向的随机性,为0 和1 之间均匀分布的随机数。,在实验中设定,σ=0.1~1 m2/sec2,T=Δt/2, Δt 为选取的时间间隔,dw 服从均值为0,2Δt 方差为的正态分布,取值概率满足式1-8。 1.3.2 改进的Leeway 模型的仿真 仿真参数如表2 所示。 表2 仿真参数 设定海况为3 级以下,海表面风速在1.5 ~2.0 m/s,传感器网络的运动情况如图1 所示。传感器节点部署在1 000×1000(m2) 的监测海域内。最小圆圈内的点为节点的初始位置,星号为节点的当前位置(分别是2、4、6…20、22、24 小时后节点的位置)。 整个光合作用途径的转变是一个十分复杂的过程,涉及到很多基因。而光合作用途径的转变是可逆的,在去除盐胁迫后,PEP羧化酶的转录和酶活均大幅度下降[40]。 整个网络的运动状况决定于风海流和潮流,随着时间的推移,节点逐渐偏移初始位置。由于潮流的作用偏移量没有一直增加,每当潮流方向改变1次,偏移量也会改变,同时,扩散作用也越来越明显,网络成散开状,节点之间的距离在逐渐的增加。这两点从图1.1 中也可以看出来,图1.1(a)中,节点逐渐偏离初始位置,而接下来的(b)、(c)、(d) 偏移量并没有按照这种趋势一直增加,扩散作用越来越明显,网络成散开状。因此,不同于在陆地上部署无线传感器网络,在海洋上,风海流和潮流作为主要影响因素,导致无线传感器网络无规则运动,节点偏移和扩散影响了整个网络的感知能力,进而影响了传感数据的可用性,导致传感数据的可用性具有实时性的特点。 图1 传感器的运动情况 本节将综合考虑传感器节点的感知能力、能量消耗和海洋中节点的运动模型,针对数据质量中的数据可用性,建立面向海洋应用的传感数据可用性综合评判指标及方法,主要从数据的可靠性和时效性两个方面对传感数据的可用性进行评价。 假定同一监测区域内的同构数据源在系统单位时间内是同步的,则每个时间片内n 个同构数据源共同产生多源多模态数据。假设目标区域大小为S× S,将其分成N × N 个小方格,设gij(1 ≤i ≤N,1 ≤j ≤N) 为目标区域内的一个小方格,设S= {s1,s2,…,sn} 为目标区域内可以进行感知的所有传感器节点的集合,则传感数据的可靠性和时效性的度量方法如下。 利用对目标监测的结果中可靠数据占整体的比例来衡量传感数据的可靠性,假定Re(gij)为一个方格传感数据的可靠性,联系无线传感器网络的探测概率模型,定义对于∀gij有, 式中:Re(sk,gij)表示数据源感知到gij的数据的可靠性,d(sk,gij)为数据源sk到格点gij的距离,Rmax是单个数据源感知的最大距离。 则对于∀gij感知数据可靠性定义为: 根据式(2-1) 和式(2-2),可以计算出目标区域中每个格点的感知数据的可靠性,记为(xi,yi,ri),其中xi是格点的横坐标,yi是格点的纵坐标,ri是格点(xi,yi) 的可靠性。为了向用户多角度的直观的展示目标区域的传感数据可靠性,可以基于以上信息绘制对应的三维图和等高线图。作为示例,在300×300 单位的监测区域内随机部署80个传感器节点,利用式(2-1) 和式(2-2) 计算出目标区域中所有格点的可靠性,得到了图2 和图3 的三维图和等高线图,从中能够清晰的看到目标区域中传感数据的可靠性的状况。 图2 网络的感知数据可靠性三维图 图3 网络的感知数据可靠性等高线图 对于一个区域来说,仅知道一个小格点的传感数据可靠性是远远不够的。要得到一个区域的传感数据可靠性,首先针对传感数据可靠性定义一个阈值Remax将∀gij的感知数据可靠性Re(gij)映射成一个二值数据re(gij),即 时效性是指相对于当前任务,数据是最新数据的程度。一般用时效性来考察数据的时间特性对应用的满足程度。数据从产生、发展、到消亡,有一个相对的有效期。不同类型的应用对数据的时间特性有不同的要求。 针对海洋环境监测,随着时间的推移,WSN很可能随着海水漂流到其它海域,同时节点向接收端传送数据时要消耗能量,进而节点逐渐失效,两种原因导致无线传感器网络对海洋环境无法做到持续监测。因此本文将引入刘磊等人的文献中特定区域的持续监测时间这一概念,对于特定区域D的持续时间,表示为Tlast(D)|λ,用来衡量WSN 对于特定监测区域的监测能力,并反映数据质量的时效性。 为了研究任意网格点的感知数据的时效性,本文也利用网格的持续时间这一概念来衡量。定义对于∀gij有 式中:Ta<λ(gij)表示网格点gij数据可靠性Re(gij)<λ时对应的时刻,T0(gij)表示数据可靠性Re(gij)>λ的初始时刻,由于海洋环境的特殊性,必须强调,在整个Tlast(D)|λ 内,必须保证数据可靠性Re(gij)>λ。但由于传感器的运动复杂,每个格点的持续时间并没有办法计算,所以将这个持续时间映射到传感器节点上,用传感器节点的持续时间Tlast(Sk)研究后续问题。 本节根据第二节定义的传感数据可靠性和时效性的度量方法,提出两个应用——采集船的航行路线评价和数据源的选择。 对船在航行过程中收集到的传感数据的可用性进行评价,是本文算法的一个重要应用。 首先按照用户给定的监测粒度对监测区域进行划分,计算得到每个网格的传感数据可靠性和每个传感器节点的持续时间的值。然后根据船的实际路线信息,计算出船实际航行时所途经的所有网格。最后根据式3-1 对船航行时整个路线的传感数据可用性进行评价。 式中:w(pk)是船途经的第k 个网格gij的传感数据可靠性对应的权值,w(pk)可以根据对此网格采集的兴趣度来确定。tk是一个时间戳。Re(pk)是对应网格点的tk时刻的传感数据可靠性。n 为船的航行路线所经过的所有网格点的数量。Avg(U)为船的航行路线的传感数据可用性的评价指标。 问题描述:假设对于传感器节点分布较密集的区域内的一个网格点gij,设有n 个传感器节点{s1,s1,s2,…,sn} 对网格点gij进行感知。那么在此网格点处,由于传感器节点间的探测区域存在交叉,可能造成数据的冗余。当然,在传感器节点部署比较稀疏的区域,有些网格点的周围不存在满足条件的传感器节点,可能造成了数据的“空洞”。特别是在海洋环境中,随着海面环境的不断变化,传感器的位置是不确定的,因此传感器网络的拓扑结构也是动态变化的。如图4 所示,表示t 时刻某海域的传感器网络的拓扑结构。从(a) 图中可以看出在该时刻,传感器节点的分布是不均匀的,即某些监控区域内传感器节点过多,而很大一部分监控区域内无传感器节点。 图4 传感器网络拓扑结构图 对于传感器节点分布较密集的区域,由于传感数据的时间和空间相关性,多个传感器节点间的传感数据是很相似的,若每个传感器节点均将自己感知到的数据传输给汇聚节点,根据节点能耗模型可以知道,传感器节点传送数据给汇聚节点所消耗的能量占其本身能量消耗的一个很大比重,因此,会造成资源的极大浪费。另一方面,要对传感数据进行处理,那么处理大量的相似甚至相同的信息,也会造成相关资源的浪费。在此情景下,本节针对监测区域内任意一个网格点,提出基于可用性的数据源选择算法,旨在保证数据质量的前提下,选择合适的数据源将其传感数据上传给汇聚节点同时保证数据的传输代价最小。 本文首先针对任意一个对网格点gij起作用的传感器节点sm,定义一个数据源选择的指标Cs: 式中:Re(sm,gij)表示数据源sm感知到gij的数据的可用性,tlast(sm)表示传感器节点的持续时间。 根据定义,首先计算出n 个传感器节点对网格点gij的传感数据的可靠性集合Re = {Re(s1,gij),Re(s2,gij),…,Re(sn,gij)},和n 个传感器节点的持续时间集合Tlast= {tlast(s1),tlast(s2),…,tlast(sn)},这样就能计算出数据源选择的指标集合CS = {Cs1,Cs2,…,Csn}。对CS 集合的所有数据进行排队,排队顺序是由大到小。选择前k 个指标对应的传感器节点作为网格点gij的数据源,将传感到的数据上传给汇聚节点,同时,利用传感器硬件技术,使其它节点休眠以节省资源。 k 的指定是一个重要问题,要综合考虑用户的要求和实际监测环境的要求。 对于没有传感器节点的空白监控区域,汇聚节点可根据该区域的历史数据以及下一时刻的感知数据,利用插值技术(如Hermit 插值和Spline 插值)对该监控区域数据进行预测以保证感知数据的可用性。 这节通过实验展示上述综合评价方法和评价过程,求出任意T 时刻的数据可靠性,并实现两个应用——采集船航行路线的评价和数据源的选择。 图5 为程序运行之后的截图(系统运行了能耗模型和可靠性度量方法)。分别得到了T 时刻的剩余节点数和监测海域初始时刻的数据可靠性) 其中在对话框的左侧显示了部署传感器节点的数目、传感器节点的位置信息、能耗模型的相关参数、网格点划分粒度,最终给出本次模拟区域的数据可靠性。在对话框的右侧显示了T 时刻剩余的节点数、剩余节点的初始位置信息等。 图5 运行截图——得到T 时刻剩余节点 图6 运行截图——初始和T 时刻节点位置对比 观察图5 和图6,初始时刻,监测区域D 中部署了80 个传感器节点,此时监测区域D 的传感数据可靠性为0.852,经过T(3 600 s) 时间节点的能量消耗和运动,监测区域D 的传感数据可靠性变为0.426。说明传感器节点的能量消耗和运动对传感数据的可靠性有着巨大的影响。但仅基于T=1 h 的数据可靠性,不能推知T=2 h 的传感数据可靠性一定小于0.426,因为传感器节点的Leeway 运动模型中已经证明传感器节点的运动决定于风海流和潮流,实际环境中随着风向和潮流流向的变化导致监测区域外的节点回到监测区域内,数据可靠性就会提高。 图7 路线评价截图 图8(系统运行了3.2 数据源选择方法) 为指定网格点的数据源选择截图。其中在对话框下半部分的数据源选择部分,本文指定了特定的网格左上顶点的横纵坐标,其中横坐标为100,纵坐标为40,同时给出了k 的值为2。图的上半部分有3 个并列的网格区域,从左起,第一个网格区域展示了整个监测区域的部署情况,部署了60 个节点。第2 个网格区域展示了对指定网格有感知作用的所有数据源,可以观察到共有12 个传感器节点对此网格有感知作用。第3 个网格区域展示了针对特定网格进行的数据源选择,根据要求本文算法选择了两个数据源。 图8 数据源选择截图 然后对数据源的选择结果进行分析,在第2 个网格区域中,从每个传感器节点到汇聚节点的距离可以直接观察出传感器节点A 对指定位置的数据可靠性要高于节点B 对指定位置的数据可靠性,但是最后数据源的选择结果中有B 节点却没有A节点,原因是数据源选择算法不仅考虑了节点对网格点的数据可靠性,也考虑到了节点本身的持续时间。传感器节点的持续时间与到汇聚节点的距离有关,根据这一点,可以知道,A 节点的持续时间要小于B 节点的持续时间。 通过传感设备监控海洋环境有着广泛的应用需求,同时也面临着对感知到的环境数据进行控制和修复的诸多挑战。本文在海洋监测应用背景下,从可靠性和时效性两方面对传感数据的可用性进行形式化定义及度量,并结合传感器节点自身的能量限制,及海面环境影响下的移动性等因素,提出采集船的航行路线评价和数据源选择算法并进行了仿真实验的验证。提出的传感数据可用性评价技术有助于高质量的数据获取、清洗和分析,是建立健壮的数字海洋系统的重要基础。本文只对单一种类数据的可靠性和时效性进行了研究,未来工作计划考虑一致性和完整性等更多指标的数据质量特征,并建立多模态融合数据的可用性评价模型。 Akyildiz I F, Su W, Sankaransubramaniam Y, et al, 2002. A survey on sensor network. Communications magazine, IEEE, 40 (8) : 102-114. Erdun Zhao, Yating Lv, 2009. A Density Mobility Scheme for Improving Coverage in Wireless Sensor Networks. International Conference on Web Information Systems and Mining,725-726. Guiling Wang, Guohong Cao, Piotr Berman, Thomas F, 2007. La Porta.Bidding Protocols for Deploying Mobile Sensors.IEEE Transactions on Mobile Computing,6 (5) :563-567. Patwari N, Hero III A O, 2003. Using proximity and quantized RSS for sensor localization in wireless networks//Proceedings of the 2nd ACM international conference on Wireless sensor networks and applications.ACM,20-29. S Jain, R Shah, W Brunette, et al, 2006. Exploiting Mobility for Energy Efficient Data Collection in Sensor Networks. Mobile Networks and Applications,Springer Science,11 (3) :327-339. Savvides A,Han C,Strivastava M B,2001.Dynamic Fine-Grained Localization in Ad-Hoc Networks of Sensors.Proc.ACM MobiCom,166-179. Wang A, Heinzelman W R, Sinha A, 2001.Energy-scalable protocols for battery-operated micro-sensor networks. Journal of VLSL Signal Processing,29 (3) :223-237. Yao J,Zhang G,Kanno J,et al,2009.Decentralized detection and patching of coverage holes in wireless sensor networks//SPIE Defense,Security, and Sensing. International Society for Optics and Photonics,73520V-73520V-10. 刘磊,王小青,种劲松,等,2012.海洋监测无线传感器网络的节点数目量化分析.电子测量技术,35(5):107-113. 任丰源,黄海宁,林闯,2003. 无线传感器网络. 软件学报,14(7):1 282-1 290. 郑琳,刘艳,崔文林,等,2014.海洋监测数据质量评估研究.海洋通报,33(2):228-234.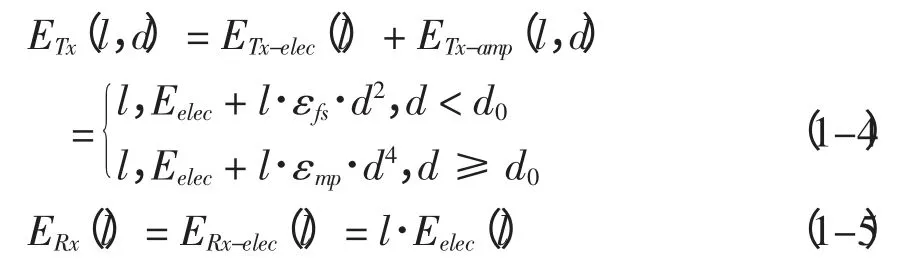

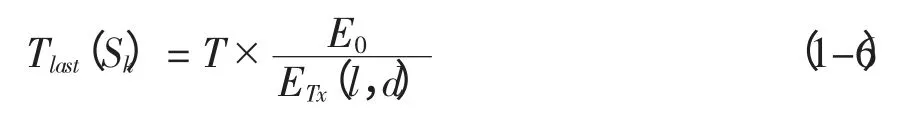
1.3 海洋背景WSN 运动模型

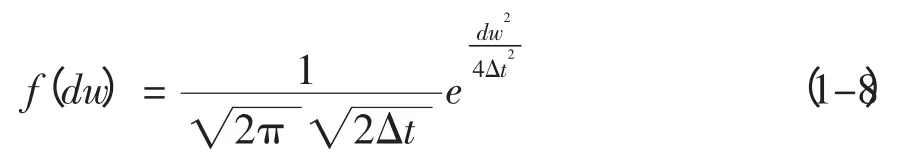
2 传感数据可用性的评价
2.1 可靠性度量

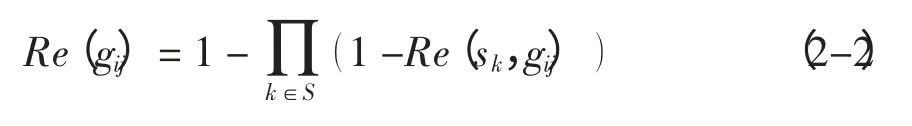
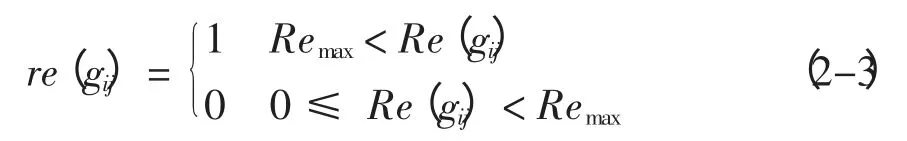

2.2 时效性度量
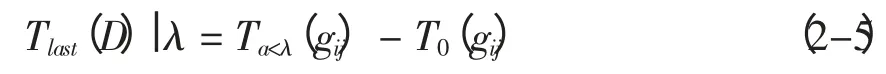
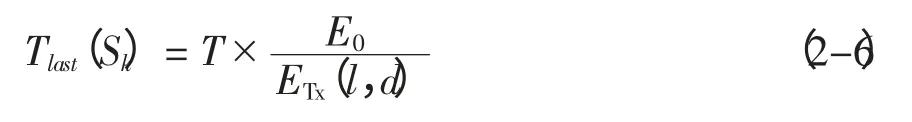
3 传感数据可用性评价的应用
3.1 采集船的航行路线评价
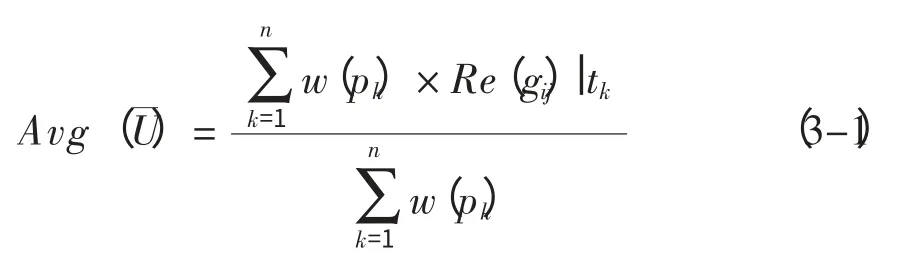
3.2 数据源的选择
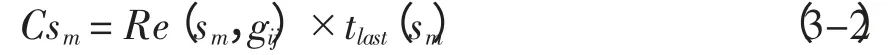
4 实验
4.1 计算任意T 时刻网格的数据可靠性

4.2 采集船的航行路线评价
4.3 数据源的选择
5 总结

