WaveWatch III和SWAN模型嵌套技术在业务化海浪预报系统中的应用及检验

徐丽丽，肖文军，石少华，堵盘军，郑晓琴，张婕，何佩东

（1.国家海洋局东海预报中心，上海 200081；2.南京信息工程大学 环境科学与工程学院，江苏 南京 211800；3.华东师范大学 河口海岸学国家重点实验室，上海 20062；4.河海大学，江苏 南京 211800）

东海海域海上运输航线繁多、海底能源矿藏丰富，是亚太区域经济最发达的海域之一。随着我国海洋权益保护力度的加大，钓鱼岛海域巡航执法的常态化，对短期航线保障预报、长期趋势决策等海洋环境预报提出了更高需求。同时东海东邻西北太平洋，近岸岛屿众多，水深复杂，冬季受强冷空气影响，夏季热带气旋频发，且这些气旋有80%的几率发展为台风，近海波浪主要受风浪影响外，还受东太平洋传播涌浪的影响。东海沿海经济发达，港口码头、重大工程等重点保障目标众多，对沿海近岸精细化海浪预报的需求迫切。如何在保证预报产品质量的前提下，节约计算资源、满足产品时效需求，实现“一套系统，多方服务”的高效率预报服务方式是关键问题之一，其中建立区域性的海浪数值预报系统是必不可少。

业务化海浪数值预报系统国外起步早，发展成熟，例如，NOAA（美国海洋大气管理局） 采用WaveWatch Ⅲ海浪模式建立了全球、阿拉斯加和西北大西洋以及美国近岸区域的海浪预报系统，发布了120 小时预报。国内主要研究工作有国家海洋环境预报中心在“十五”期间，以国际上第三代海浪数值预报模式WAM 和SWAN 为基础，建立了西北太平洋和中国近海的区域性海浪业务化数值预警系统和全球海浪数值预报系统，预报时效为72 小时。一般来说，WaveWatch Ⅲ模式常用于大洋尺度波浪计算，而考虑了更多近岸物理过程的SWAN 模式更适用于近海波浪计算，两种模式嵌套计算的方法常用于从大洋到近岸尺度的波浪模拟中（高山等，2006；李本霞 等，2010；张洪生等，2013）。已有的研究（王殿志等，2004） 所采用的都是结构网格，缺点在于无法在不大量增加计算时间的情况下，根据需要进行局部空间分辨率的加密。SWAN 模式从40.72 版本开始，可以使用无结构网格进行计算，但暂不支持与结构网格WaveWatch Ⅲ直接嵌套的接口程序（The SWAN team，2014），因此目前东海区业务化海浪数值预报系统以SWAN 自嵌套为主，远洋计算范围不够大，近岸网格不够精，同时采用OMP 并行方式，计算耗时长。

本文根据钓鱼岛海域巡航执法、精细化预报等新的海浪业务化预警报工作任务的需求，基于WRF 风场数据源，采用结构网格WaveWatch Ⅲ模式和无结构网格SWAN 模式嵌套计算，建立一套适用于东海区的海浪数值预报系统，并进行误差分析和不同设计方案的对比试验，表明此套海浪数值预报系统在保证多尺度预报产品计算精度的前提下，能够提高计算效率，节省计算资源，且满足预报产品的时效性需求，也证明此套海浪数值预报系统业务化运行的可行性和稳定性。

1 模型选择及参数设置

本文使用的海浪模式为 WaveWatch III（V3.14） 和SWAN（V40.91）。WaveWatch Ⅲ是Tolman 等（1991） 在第三代海浪模式WAM 的基础上发展起来的，是当前国际上最成熟海浪数值模式之一，具有稳定性好、计算精度高的特点，模式采用了并行计算技术，提高了模式的性能和效率，为海浪数值预报的业务化运行打下了良好的基础。SWAN 模型是由荷兰Delft University of Technology的Booij 等（1999） 借鉴和修改了原有的第三代海浪模型WAM 而建立，进一步考虑了三个一组的波波相互作用、水深引起的波浪破碎和绕射等，而且采用隐式格式离散控制方程，使该模型更适用于近岸波浪的生成和传播的数值模拟。

WaveWatch Ⅲ和SWAN 都使用了波作用量守恒方程作为其控制方程，其在球坐标下的表达式为：

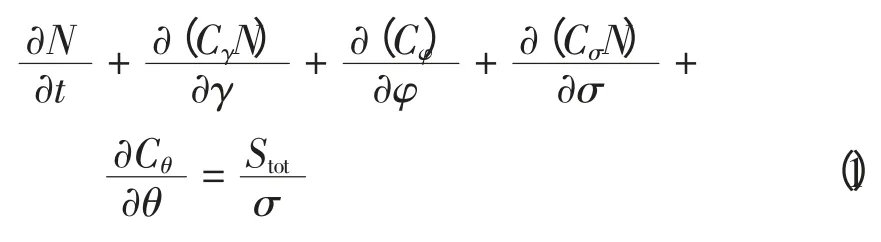
式中，N 为波作用量密度，t 为时间，γ、φ、σ 和θ 分别表示经度、纬度、频率和波向，Cγ、Cφ、Cσ、Cθ分别表示波浪在上述4 个空间中的传播速度，Stot为源函数，在WaveWatch Ⅲ和SWAN 中源函数的形式不同，详见文献（Tolman，1991；2009）。

为实现WaveWatch Ⅲ模式与无结构网格SWAN 模式的嵌套计算，需要对WaveWatch Ⅲ模式输出波浪谱文件进行处理。首先提取SWAN 模式开边界点信息，并将这些点作为WaveWatch Ⅲ单点输出，再利用WaveWatch Ⅲ的后处理工具WW3_outp 读取和转换为ASCII 单点波浪谱文件（tolman，2009），最后编程转换为SWAN 模式标准谱文件，作为SWAN 模式边界波浪谱（标准谱文件格式可参考SWAN 源代码文件swanout2.ftn）。

1.1 模型设置

1.1.1 地形资料

地形数据采用美国国家海洋大气局（National Oceanic and Atmospheric Administration，NOAA） 网站上提供的ETOPO1 数据，ETOPO1 数据是当今海洋模式中常用的水深岸线数据，它是NOAA 收集多方面资料，经过处理得到的网格化地形数据。本文选用的ETOPO1 地形数据的分辨率为1′×1′，包含了大陆的地势起伏和海洋中的水深数据，是在众多全球和区域数据集的基础上建立起来的，并且加入了冰面的数据和岩基数据，且近岸的水深地形数据已经进行过订正。

1.1.2 风场数据

本文采用的风场数据是东海预报中心东海区业务化WRF 风场模型数据，台风期间的WRF 模式边界和初始场数据采用的是美国NOAA 中心的后报FNL 数据。因为风场是海浪模型的驱动场，其准确性至关重要。本文采用的风场模拟数据均经过率定，准确性得到可靠保证（图1），下文的海浪误差分析均不考虑风场误差。

图1 风场模型计算个例比对图

1.1.3 计算区域

研究海域为东海区，计算范围（图2） 的选定综合考虑大区域台风作用和季风的影响，同时满足不同服务对象对产品的范围和精度的不同需求（图3），因此采用3 层嵌套的计算方法，具体的计算范围见表1。

表1 东海区海浪数值模型设置参数

1.2 参数设置

西北太平洋海域WaveWatch III 模式的网格数为451×381；最大全局时间步长设为600 s、x-y方向和k （在WaveWatch III 中，波作用密度谱是波数和波向的函数） 方向最大时间步长均设为600 s，最小源函数项步长设为60 s；波浪谱的最小频率为0.041 18 Hz，频率个数为36，频率步进倍数为1.1； 波浪谱方向平均分为25 个。西北太平洋WaveWatch III 模式的外边界无外部的波浪进入。

东中国海域WaveWatch III 模式的网格数为426×526；最大全局时间步长设为300 s、x-y 方向和k 方向最大CFL 时间步长均设为300 s，最小源函数项步长设为15 s；波浪谱设置同西北太平洋。东中国海的波浪边界由西北太平洋的计算结果提供。同时每小时为SWAN 输出一次边界点上的波浪谱。

长江口杭州湾海域采用SWAN 模型非结构网格计算，网格数为453 505 个，最高空间分辨率20 m，开边界点为82 个点，边界条件由东中国海海域计算结果提供。时间步长设为20 min；波浪谱的频率范围为0.02～1.20 Hz；波浪谱的方向平均分为25个。同时考虑水位的影响。其他参数采用默认值。

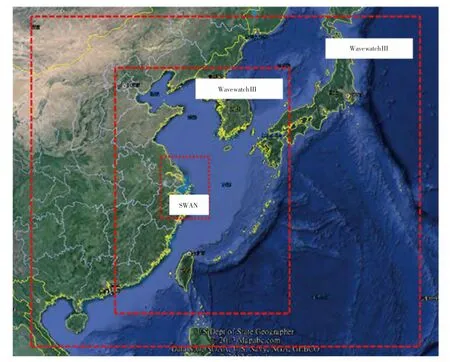
图2 东海区海浪数值模型计算范围

图3 长江口海域SWAN 模型计算网格

2 数值试验及分析

满足“时效性”和“稳定性”要求是业务化数值预报系统的前提条件，本文构建的系统基于结构网格与非结构网格嵌套计算，尤其是为避免采用非结构网格的SWAN 模型在高风速条件浅水区域，由于波浪折射引起的波能集中，容易出现数值耗散的问题（Dietrich et al，2013），设置了数值比对试验，对系统的计算耗时和稳定性进行测试。

试验一：远海深水区两套模型计算效率测试。

分别采用WaveWatch III 模式自嵌套和SWAN模型自嵌套进行西太平洋海域和东中国海海域海浪计算。

结果表明SWAN 模型与WaveWatch III 模型在各项同参数设置时（表2），WaveWatch III 模式对于远海深水的海浪数值模拟结果几乎一致（结果从略）。江丽芳等（2011） 也研究过WaveWatch III 与SWAN 模型对南海大区域海浪的模拟能力，结果表明二者的计算精度接近一致，但在计算效率上，WaveWatchIII 高于SWAN 模型，在同步采用5 个计算节点，80 个cpu 的配置下，WaveWatchIII 的计算效率提高了56 %，因此大区域采用WaveWatch III 模型在保证计算精度的情况下，计算效率将大大提高。

试验二：无结构网格SWAN 模型稳定性测试。

表2 模型计算参数设置

非结构网格的SWAN 模型在浅水区域，由于网格过粗等原因，波浪折射可能出现在一个网格点上集中过多的能量，使结果失真的问题。本研究通过对SWAN 无结构网格进行优化，水深局部调整等处理以避免出现结果失真。设计不同方向35 m/s的定常风进行数值试验，数值模拟结果（图4） 表明本系统建立的长江口海域SWAN 模型，能够确保在高风速下不出现计算失真点，能满足长江口近岸海域各海况，尤其是台风影响下的近岸海浪数值模拟。

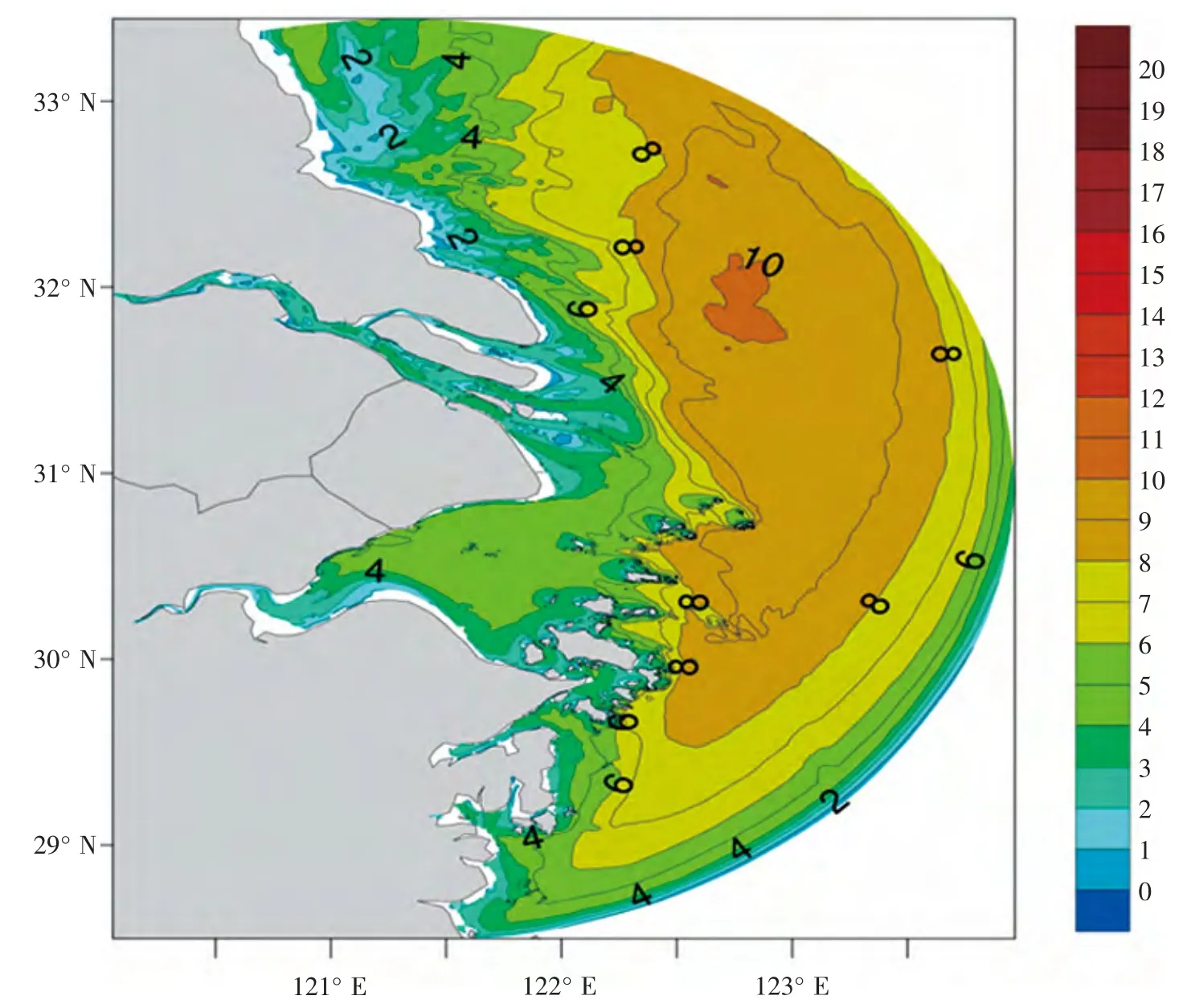
图4 长江口杭州湾海域35m/s 的东南风情况下的波浪场分布

试验三：极值风速条件下，WaveWatch III 模式精度测试。

台风期间，将预报风场和后报风场作为不同的输入源，检验WaveWatch III 模式对极值风速条件下波浪场的刻画情况。

风场的准确性对于海浪数值模拟的精度有着至关重要的作用。1307 号强台风“苏力”和1312 号台风“潭美”路径和强度相似，且都以台风强度登陆福建沿海（图5）。以QF209 浮标为例，结果显示，“苏力”的数值模拟结果好于“潭美”（图6）。“苏力”期间，QF209 浮标观测有效波高9.3 m，模型计算值为10.8 m，且波浪增长时间、趋势都与实测值一致。“潭美”影响期间，QF209 浮标21日15 时观测到最大有效波高8.3 m，数值模拟预报结果10.3 m，预报结果存在极值偏高的现象，且波高增长时间及区间提前。

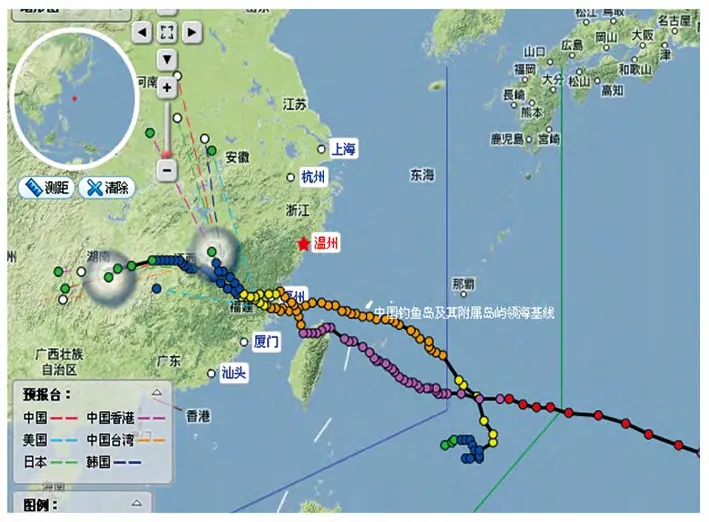
图5 “苏力”和“潭美”台风路径图

图6 QF209 浮标有效波高24 小时预报与实测比对图

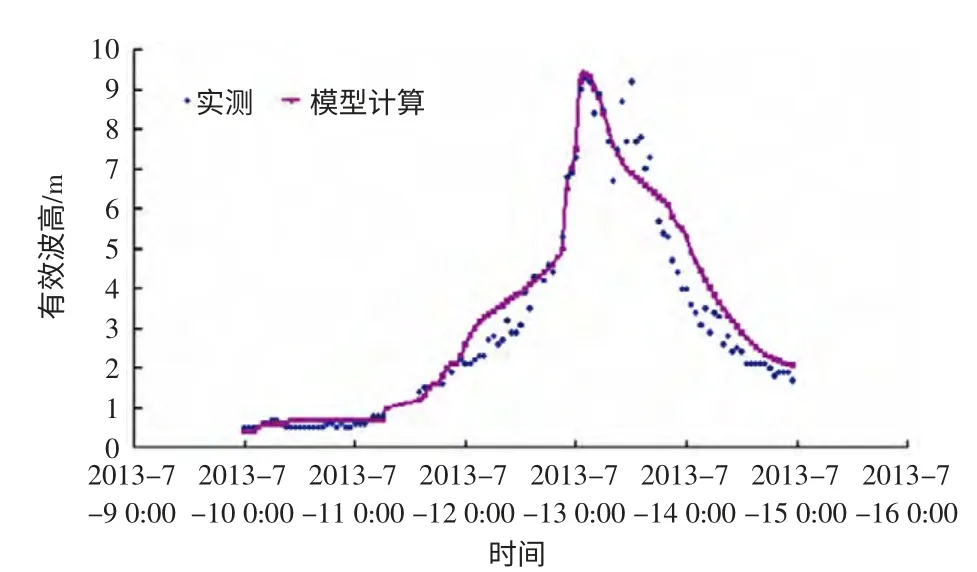
图7 “苏力”后报结果与观测对比图

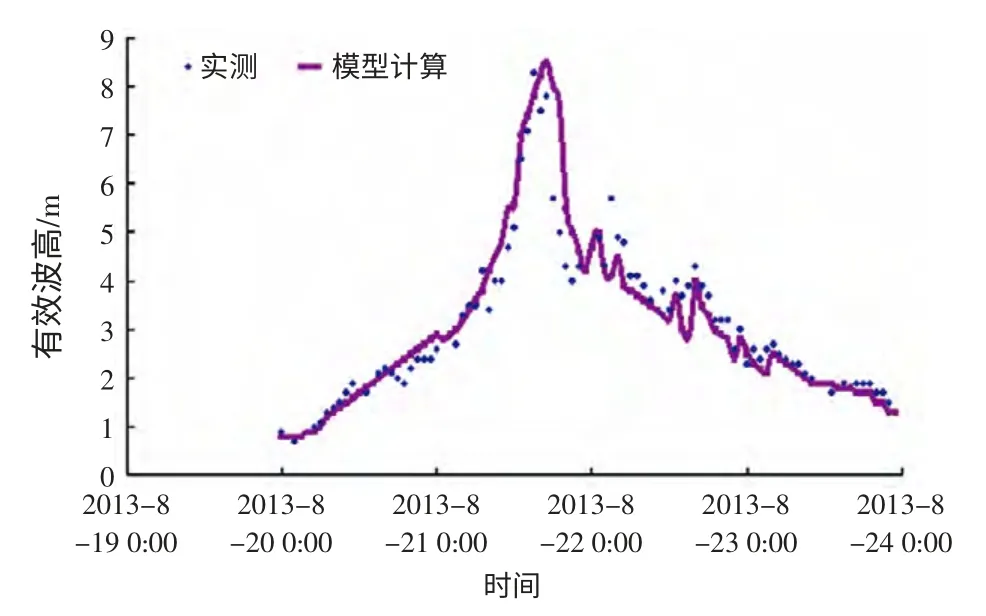
图8 “潭美”后报结果与观测对比图

作为对比试验，本文选取2 次台风过程的后报风场进行过程模拟（图7-8）。结果表明采用后报风场的数据，2 次台风过程的海浪数值模拟结果令人满意。虽然误差存在，但波高过程极值和波高变化趋势与观测值非常吻合。尤其是“潭美”台风过程，在极值量级上及波高增长时间上，后报结果远远好于预报结果，主要原因为“苏力”期间台风路径预报准确且过程中台风路径和强度滚动调整幅度小。而“潭美”台风在强度预测上远远大于实况，路径也在预报过程中不断的调整和修正。因此可见，海浪数值预报模型的准确性除了系统本身的参数设置和调整外，尤其是台风过程，台风的路径预报准确性起着至关重要的作用。

3 系统验证及结果分析

3.1 模型验证资料及海洋站位说明

本文所用的实测资料是东海区海洋台站大戢山海洋站及海上浮标的逐时观测资料。其中浮标数据的时间序列为2013年7月1日00 时至2013年8月30日23 时，浮标为逐时整点数据（站位见图9）。

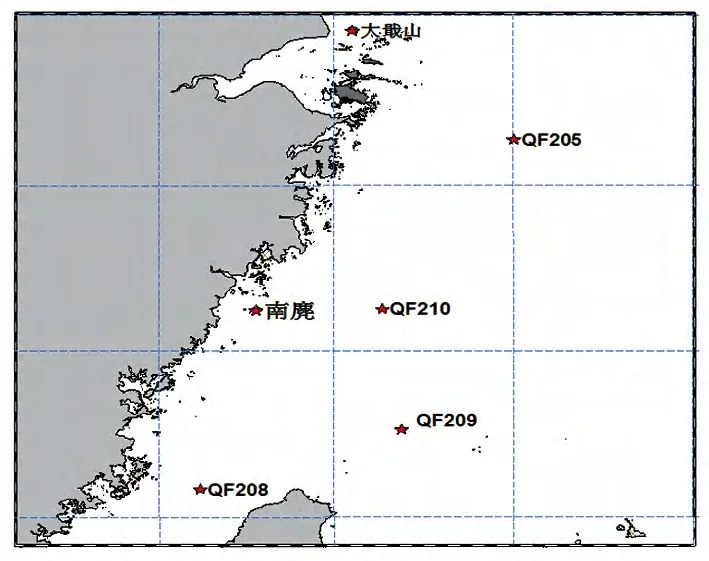
图9 东海区观测站点位置分布图

大戢山岛系长江口与杭州湾交汇处孤岛，面积仅0.07 km2。测站海拔高度81 m，测得的风速比海面大。该海洋站的测波点位于岛屿的东北角，朝向NE，视野开阔，来自NNE—E 向的波浪有很好的代表性。大戢山海洋站的海浪观测方式为人工观测，每3 小时1 个观测数据（分别为08、11、14、17）。文中采用的观测数据时间序列为8月9日00 时-29日12 时。

3.2 大区域WaveWatch III 模式预报结果趋势检验

东中国海的海浪计算利用西太平洋提供的边界条件，可以很好地考虑到涌浪及尺度的影响，可以更精确地模拟波浪场。 图（10-21） 给出了2013年7月1日—8月30日期间浮标和海洋站有效波高的观测值和计算值的24 小时、48 小时、72 小时的比对结果，模型计算结果较好地模拟了有效波高的变化趋势，吻合程度较好。即使在台风影响期间，虽然模型存在“极值偏估”的现象，但波浪总体变化趋势的刻画仍然具有一定的参考价值。7月和8月东海区主要受太平洋副热带高压控制，观测波高的总体平均值不大；随着副高的东退和西进，但也会存在明显的起伏变化过程，数值模拟的结果也很好地刻画波动变化趋势。

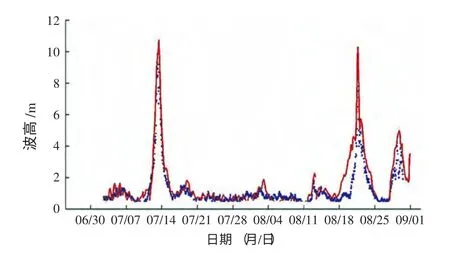
图10 QF 209 预报值与观测值对比（24 小时）

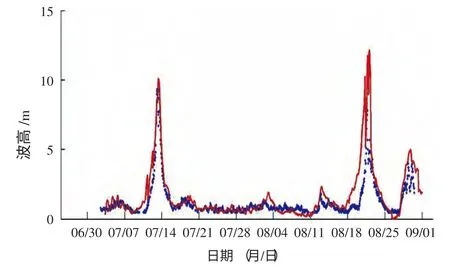
图11 QF 209 预报值与观测值对比（48 小时）

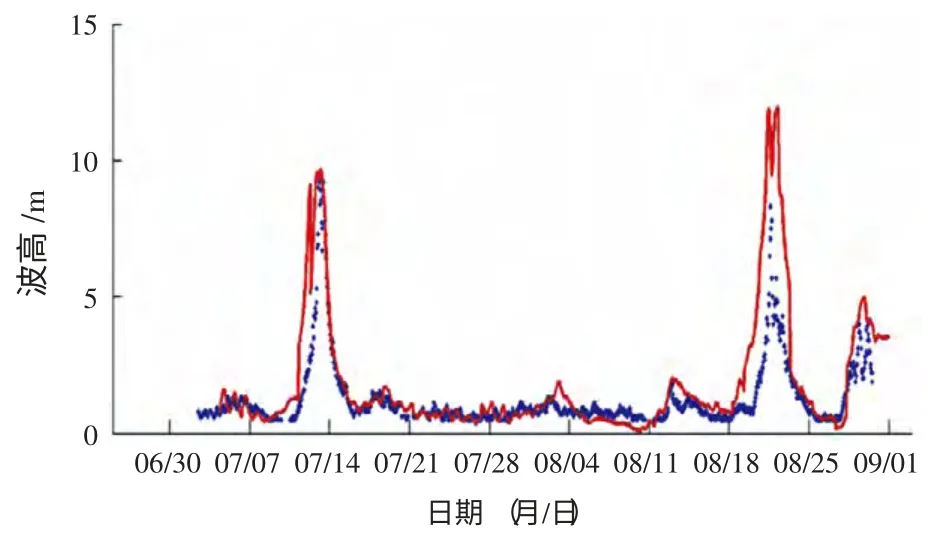
图12 QF 209 预报值与观测值对比（72 小时）

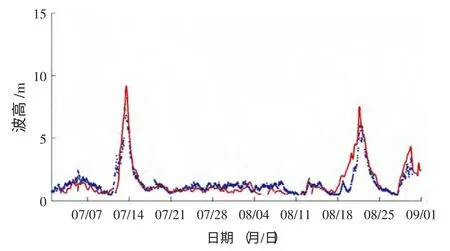
图13 QF 210 预报值与观测值对比（48 小时）

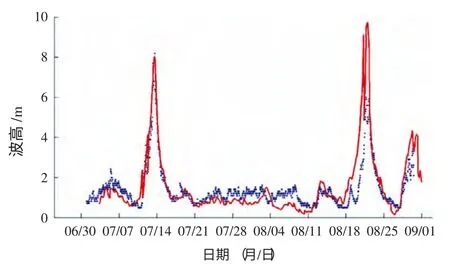
图14 QF 210 预报值与观测值对比（48 小时）

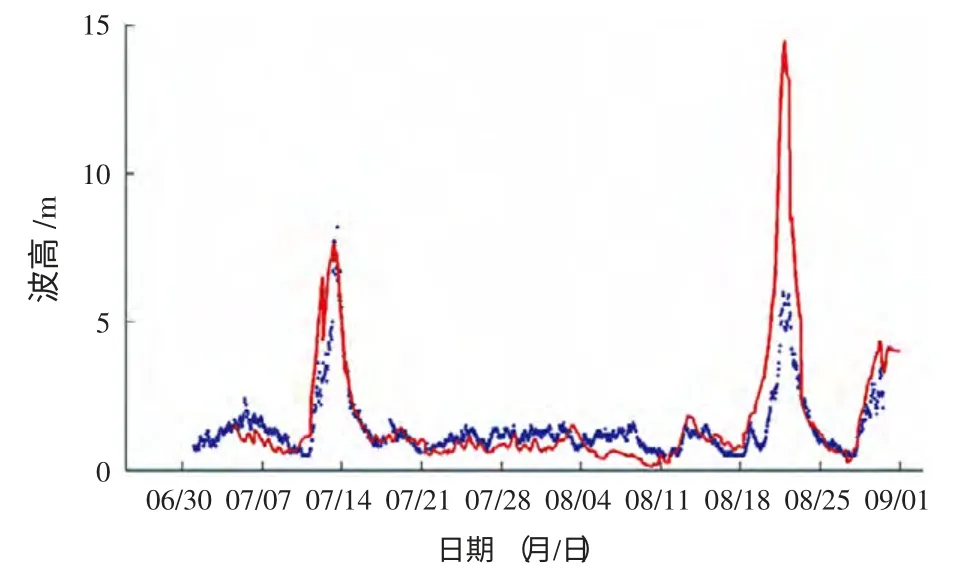
图15 QF 210 预报值与观测值对比（72 小时）

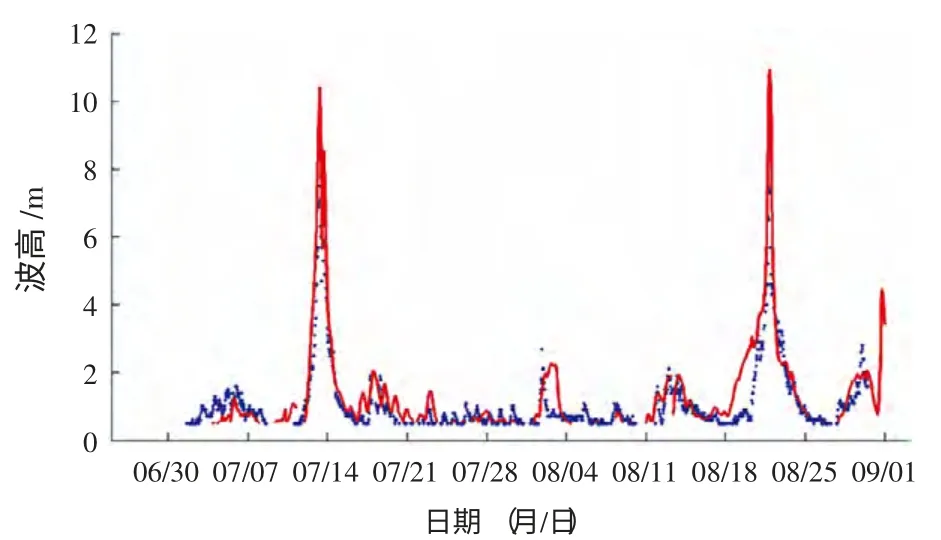
图16 QF 208 预报值与观测值对比（24 小时）

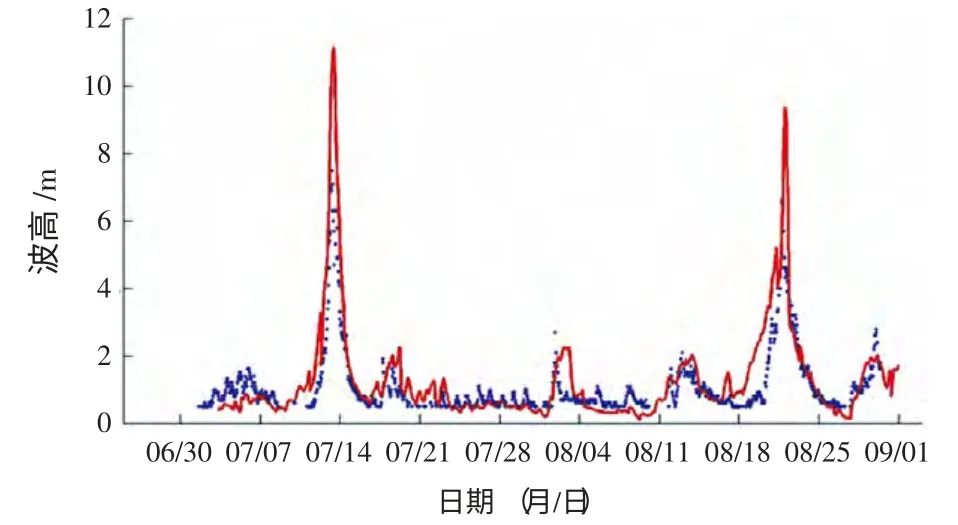
图17 QF 208 预报值与观测值对比（48 小时）

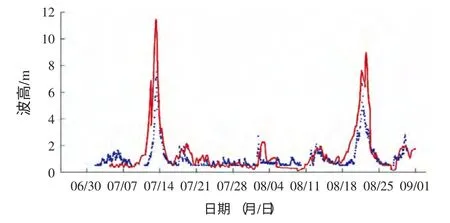
图18 QF 208 预报值与观测值对比（72 小时）

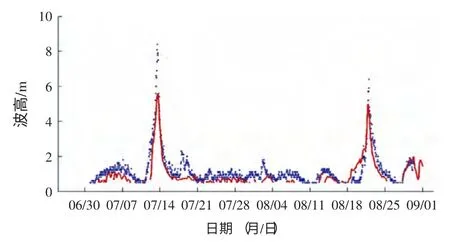
图19 南麂站预报值与观测值对比（24 小时）

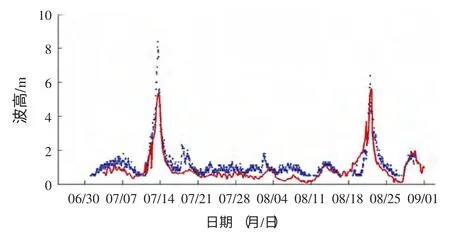
图20 南麂站预报值与观测值对比（48 小时）

检验结果表明在普通天气条件下，WaveWatch III 可以较准确提供不同尺度分辨率和精确性的波浪场，且较好描述大区域波一波非线性相互作用。但在水深较浅的近岸，WaveWatch III 的模拟结果不甚理想（图21）。主要是因为WaveWatch III 模式计算采用的是矩形网格，不能精细化的刻画长江口杭州湾的复杂地形。同时WaveWatch III 模式采用了深水条件下的弥散关系，这是线性化波浪控制方程所得到的，虽然模式对浅水加了修正项，但对于有限水深，非线性作用明显的时候模式精度还是不足，特别是对有限水深的短波的模拟显得不足。

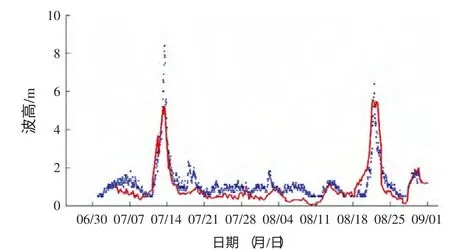
图21 南麂站预报值与观测值对比（72 小时）

3.3 近岸小区域SWAN 模式预报结果趋势检验

WaveWatch III 模式对有限水深的模拟存在不足，为满足沿岸港口码头等重点保障目标的精细化预报的需求，近岸采用WaveWatch III 和SWAN 模式嵌套计算。修改WaveWatch III 和SWAN 的嵌套接口，利用WaveWatch III 模拟大区波浪场，输出小区嵌套边界的二维谱，并将边界谱值赋给SWAN，为小区域的波浪场计算提供边界条件。模式的嵌套接口不要求两套模式谱空间设置一致，但为了保证连续性，将两套模式的谱空间设置相同。

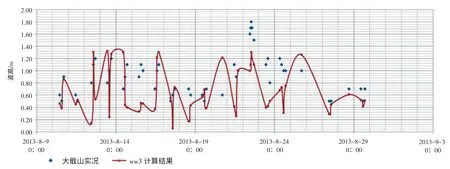
图22 大戢山海洋站WaveWatch III 模型输出结果与实测比对图

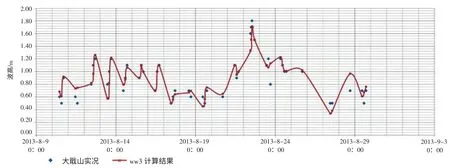
图23 大戢山海洋站SWAN 模型输出结果与实测比对图

图22 给出了大戢山海洋站有效波高的观测值和 WaveWatch III 模式输出结果的比对，WaveWatch III 模式模拟计算结果与实况的平均绝对误差为0.34 m，平均相对误差为43%。显示计算的有效波高小于观测值，且变化趋势模拟精度不高。图23 显示了SWAN 模型的计算精度得到了明显改善，平均绝对误差为0.13 m，平均相对误差为24%。说明采用嵌套方案，使得风浪可以充分成长或者能充分考虑涌浪对计算站点结果的影响、边界条件的处理也更加合理，还能节省计算耗时。同时也证明本系统建立的SWAN 模型，其地形数据精细，网格设置合理，更适合长江口海域近岸浅水波浪的数值模拟。

3.4 海浪数值预报系统的误差分析

基本统计检验参数绝对误差AE、相对误差RE、平均绝对误差MAE、平均相对误差RAE 计算结果进行定量分析（表3）。计算公式如下：

绝对误差：

相对误差：

其中Ci为计算值；Oi为观测值。

表3 计算结果表明：24 小时的平均绝对误差在0.12～0.32 m 之间，平均相对误差在13%～21%之间；48 小时的平均绝对误差在0.13～0.54 m 之间，平均相对误差在22%～34%之间；72 小时的平均绝对误差在0.11～0.70 m 之间，平均相对误差在31%～50%之间。总体24 小时误差好于48 小时好于72 小时，误差极值主要由台风过程引起。去除台风过程后，QF 209 浮标的预报精度提高显著，72 小时之内的预报误差平均绝对误差在0.23 m 以下，相对误差在23%以下，表明在普通天气条件下，WaveWatch III 能够准确提供不同尺度分辨率的波浪场。

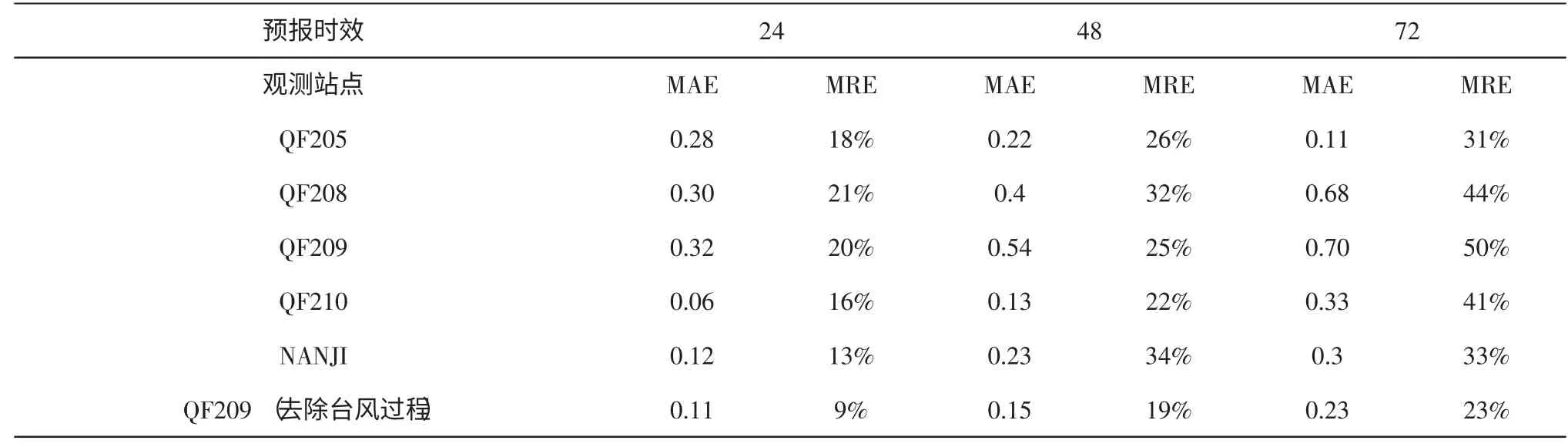
表3 各观测站点24、48、72 小时预报误差分析

为了分析预报误差的主要分布区间，将各统计样本的绝对误差AE 和相对误差RE 进行分级累积频率统计（图24），可以明显看出误差的主要区间分布。计算公式为如下

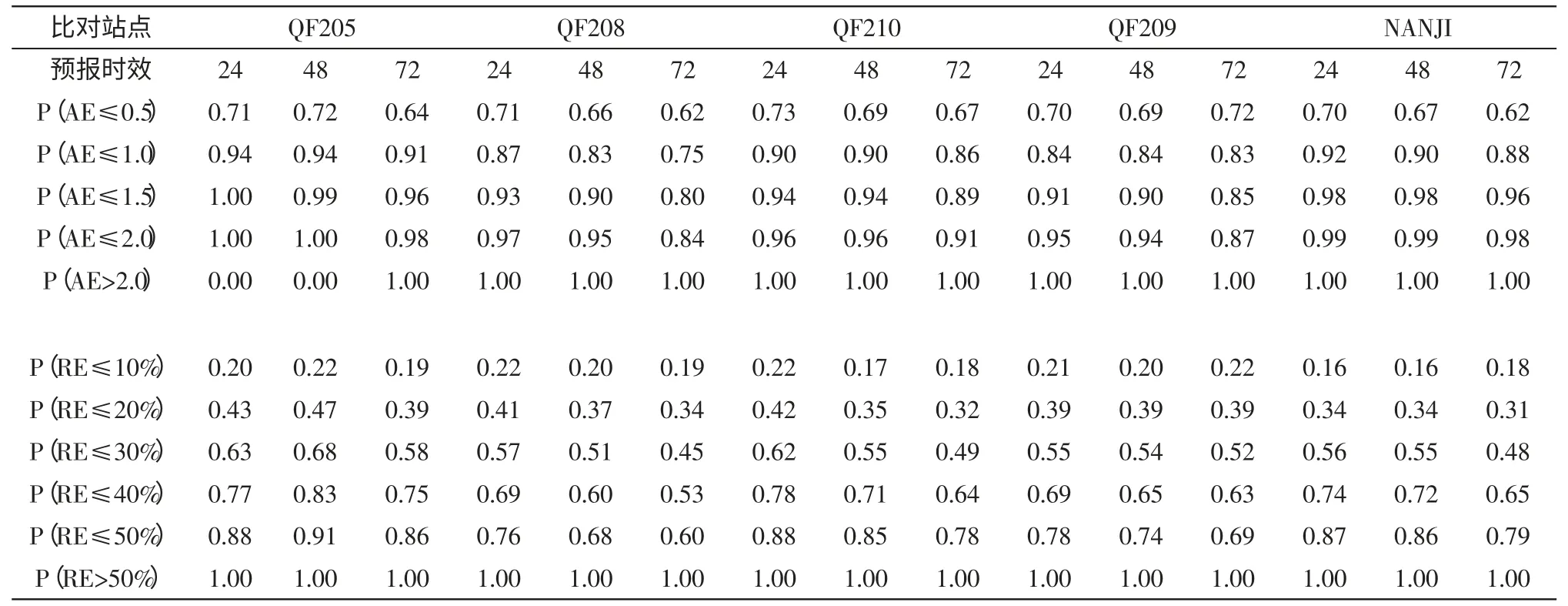
表4 各观测站点24、48、72 累积误差分析表

绝对误差出现概率：

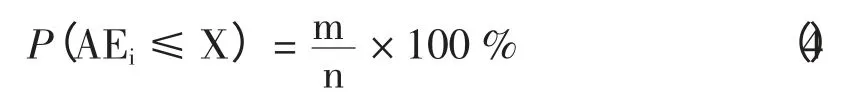
相对误差出现概率：

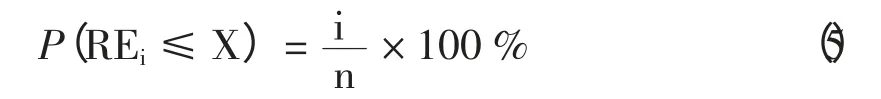
表4 显示浮标的有效波高24 小时、48 小时和72 小时的平均绝对误差小于0.5 米的出现概率在70%左右，海洋站平均绝对误差小于0.5 m 的出现概率相对较低，但也维持在60%以上。平均绝对误差小于1.0 m 的出现概率达到80 %左右，平均绝对误差小于1.5 m 的出现概率达到几乎达到95%，2 m 以上的极值过程主要是由台风引起的。平均相对误差小于30%的出现概率达到60%，说明模型结果的可用性。平均相对误差大于50%的出现概率占极少数，同样是由于台风过程引起。

4 结论

本文根据钓鱼岛海域巡航执法、沿岸重点保障目标精细化预报等海浪业务化预警报工作需求，基于中心研发的WRF 风场数据源，采用结构网格的WaveWatch III 和非结构网格的SWAN 模型嵌套计算，建立一套适用于东海区和沿海近岸的海浪数值预报系。结果表明：

（1） 本文建立的数值预报系统，大区域采用WaveWatch III 模式，计算效率得到显著提高，系统的“时效性”得到保证。

（2） 近岸区域采用SWAN 模型非结构网格计算，通过对网格进行优化，水深平滑等处理，确保高风速条件下不出现数值耗散问题，保证了系统的“稳定性”。

（3） 台风过程虽然存在“高值高估”的现象，但波浪的增长趋势和变化区间仍值得参考和借鉴。通过后报风场对比试验，波浪模拟精度显著提高。说明高风速条件下WaveWatch III 模型能较准确模拟海浪场，但风场预报的准确性对海浪模拟至关重要。

（4） 误差分析表明WaveWatch III 能够准确提供均有不同尺度分辨率的波浪场，预报24 小时平均绝对误差在0.3 m 以下，平均相对误差在20 %以内；预报48 小时的平均绝对误差在0.5 m 以下，平均相对误差在35%以内；72 小时平均绝对误差在0.7 m 以下，平均相对误差在50%以内。

（5） 相较于大面，WaveWatch III 近岸站点结果模拟不理想。近岸选取SWAN 模型，采用非结构网格与结构网格嵌套计算方案，模拟结果与大戢山的实测资料比对，平均绝对误差为0.13 m，平均相对误差为24%，模拟结果显著改善。

Booij N,Ris R C,Holthuijsen L H,1999.A third-generation wave model for coastal regions-1. Model description and validation. Journal of Geophysical Research,104 (C4) :7649-7666.

Dietrich J C, Zijlema M, Allier P E, et al, 2013. Limiters for Spectral Propagation Velocities in SWAN.OceanModelling,70:85-102.

The SWAN team, 2013. SWAN user manual, SWAN Cycle Ⅲversion 4.01.

Tolman H L, 1991. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. Journal of Physical Oceanography,21 (6) :782-797.

Tolman H L. User manual and system documentation of WaveWatch Ⅲversion 3.14. NOAA， 2009. http：//polar.ncep.noaa.gov/mmab/papers/tn276/MMAB_276.pdf.

高山，丁平兴，朱首贤，2006.WaveWatch 的操作系统移植及其与SWAN 嵌套接口的改进，海洋科学进展，24（2）：228-237.

江丽芳，张志旭，2011.WaveWatchⅢ和SWAN 模式在南海北部海域海浪模拟结果的对比分析.热带海洋学报，30（5）：27-37.

李本霞，吴淑萍，邢闯，等，2010.近海近岸高精度海浪业务化数值预报系统.海洋预报，27（5）：1-6.

王殿志，张庆河，时钟，2004.渤海湾风浪场的数值模拟.海洋通报，23（5）：10-18.

张洪生，辜俊波，王海龙，等，2013.利用WaveWatch 和SWAN 嵌套计算珠江口附近海域的风浪场.热带海洋学报，32（1）：8-17.