南黄海辐射沙脊群西洋水道污水输移扩散研究

周智鹏，陶建峰，张长宽，徐凡，姚静

（1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学 港口海岸与近海工程学院，江苏 南京 210098；3.中国科学院南京地理与湖泊研究所 湖泊与环境国家重点实验室，江苏 南京 210008）

图1 模型区域及点位示意

随着沿海地区快速的工业化、城市化及经济的迅猛发展，环境问题日趋严峻，越来越多有害于人类和其他生物的农工业污水直接排入天然水体中，江苏沿海城市港口建设的突飞猛进发展更是印证了这点（陈红卫，2011），所以弄清污水在海域中的输移扩散规律及其在水体中的稀释情况具有现实意义。西洋是南黄海辐射沙脊群北部最大的靠岸深水潮汐通道，由小阴沙、瓢儿沙分为东通道和西通道，该海域有小阴沙、月亮沙、瓢儿沙、三沙丫子、东沙等水下沙脊，地貌特征十分复杂（图1）。进入黄海的东海前进潮波和黄海逆时针旋转潮波在辐射沙脊群北面叠加形成移动性驻潮波，由西洋传入辐射沙脊群内部，在西洋海域形成了往复流的流动特性。2008-2009年国家海洋局大面观测时，测得西洋最大水深为34.9 m。西洋海域属正规半日潮区，且为强潮流区，平均大潮流速为1.5 m/s 以上，涨潮平均流速大于落潮平均流速，主流方向与岸线平行。从涨落潮历时来看，西洋海域涨落潮时间比为0.65～1.17，潮汐不对称性明显，平均潮差较大，为2.5～4 m。水动力条件复杂（王颖，2002）。自20 世纪50、60年代二维水动力数学模型产生以来，在江苏海域不断得到应用（张长宽等，1999；徐凡等，2013），但对复杂水动力条件下污水输移扩散的研究较少（龚政等，2002）。本文基于平面二维潮流和污水输移扩散数学模型，模拟了南黄海辐射沙脊群西洋海域的潮流场和污水扩散场，得到了不同水深水动力条件下污水的扩散范围及分布规律。取得成果对海岸功能区合理划分及排污工程合理选址具有一定的参考价值，并对近海环境的保护和海洋生态系统的良性循环有一定的指导意义。文章的最后拟合了污水不同排放量与其对应稀释度等值线包络面积的关系曲线，发现在两种不同稀释度条件下，两者呈良好的幂级数关系。

1 数学模型

水动力模块建立在N-S 方程的基础上。南黄海辐射沙脊群西洋海域属宽浅型水域，而且流速垂向分布较均匀，因此采用沿水深平均的二维ADI法对控制方程组进行离散求解，并引入干湿网格法来处理动边界（陶建峰等，2005），对辐射沙脊群西洋海域的二维潮流场和污水输移扩散场进行了模拟。

1.1 二维浅水潮流运动方程

假设海水匀质且不可压缩，水体运动可用如下直角坐标系的平面二维浅水潮流方程组描述，其方程为：

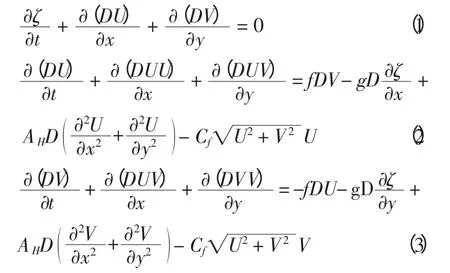
式中：x、y 为空间水平坐标；D=H+ζ 为全水深，H 为静止水面到水体底床的距离，ζ 为自静止水面起算的水位；U、V 分别为垂线平均流速在x、y 方向的分量；f=2ωsinφ 为科氏力参数，ω 为地转角速度，φ 为计算水域的地理纬度；g 为重力加速度；AH为水平紊动粘性系数；Cf为床面阻力系数。

1.2 污水输移扩散方程

式中：C 为沿水深平均的污水浓度；Dx、Dy为沿x、y 方向的污水扩散系数；Sc为污染源强度。本文为守恒污水输运扩散计算，不考虑其沉降和降解的作用。

1.3 模型参数与范围

模型范围北起新洋港口，南至东凌港口（图1），东西横跨100 km，南北相距160 km。为合理选取计算域，避免计算机存储容量浪费，计算时将其顺时针旋转20°。采用矩形网格离散，网格尺寸为100 m×100 m；流场计算的时间步长取为60 s；床面阻力系数（糙率） 取值随水深变化而改变，当全水深D≤1.0 m，Cf=0.025；D>1.0 m，Cf=0.012+0.013/D；初始条件以零启动的形式给出；在物质输移扩散模型中，污水扩散浓度场计算的时间步长为600 s；污水排放量取为20 万t/d，排放口源强取相对浓度为100。污水纵向扩散系数DY=5.0 m2/s，横向扩散系数DX=0.05 m2/s（河海大学，1995）。

由于计算海域水下地形异常复杂。随着潮位的涨落，潮滩和沙脊存在淹没和陆露交替的现象，即在计算过程中，计算域是变化的。采用干湿网格法来处理动边界。干湿法是在计算中令干点（即陆露点） 的流速为零。判别某计算点干出或淹没的标准是用该点的全水深Di，j。在实际计算中，当Di，j≤0时，动量和连续方程失去物理意义。引入标准水深D0（计算中D0= 0.005 m） 进行干湿判断。当Di，j≤D0时，（i，j） 单元被考虑为干出单元。在求解每个1/2Δt 时间层时，首先进行干湿判断。对于nΔt→（n+1/2） Δt 时间层，x 向流速分量U 计算点（i+1/2，j） 的水深分布如果满足：①Di+1/2，j＞D0，Di，j＞D0，Di+1，j＞D0或②Di+1/2，j＞D0，Di，j＞D0，Di+1，j≤D0且ζi，j- ζi+1，j＞0 或③Di+1/2，j＞D0，Di，j≤D0，Di+1，j＞D0且ζi+1，j- ζi，j＞0；3 个条件之一，则该点为湿点，按离散方程计算Ui+1/2，j，否则为干点，即Ui+1/2，j=0。对于（n+1/2） Δt→（n+1） Δt 时间层y 向流速分量V 计算点（i，j+1/2） 作类似判断；流速开边界根据Orlanski 辐射条件来确定（Blumberg et al，1985；Orlanski，1996）。其水边界由东中国海潮波数学模型提供（张东生等，1996）。物质扩散模型中岸边界的污水浓度法向梯度为0，水边界取污水流入计算域浓度为0，污水流出计算域时，污水输移扩散方程改写为式（5）：

初始时刻受纳水体浓度取为0。在实施计算中，为了更加真实反映污水在天然潮流场携带下的输移扩散，进行了60 个潮周期的潮流和物质扩散场的模拟，污水扩散浓度在30 个潮周期后处于稳定状态。

1.4 潮位潮流数值验证

选大丰港潮位站为潮位验证点，1#、2#、3#3个测流站为流速流向验证点（图1）。数值模拟时间段为2009年11月17日零时-12月23日零时，包含完整的大、中、小潮周期。潮位和流速验证资料取用2009年12月1日4 时-12月2日7 时的水文测量资料。潮位过程的计算值与实测值比较见图2；潮流流速大小、方向过程的计算值与实测值比较见图3。结果表明，潮位的计算结果与实测的潮位过程吻合良好，流速流向量值上存在一定误差，但总体吻合。潮位和流速流向的验证过程符合《海岸与河口潮流泥沙数值模拟技术规程》 （JTS/T 231-2-2010） 的要求。西洋海区的涨潮流向大致为200°，落潮流向为20°，总体呈明显往复流流态，但局部潮流方向一定程度上受滩涂地形和深槽位置的影响，涨潮流速明显大于落潮流速。图4 给出了模型大潮涨落急流场图，计算得到的西洋海域流态与（王颖，2002） 文献得到的结果一致。

2 污水稀释扩散模拟

图2 大潮潮位验证

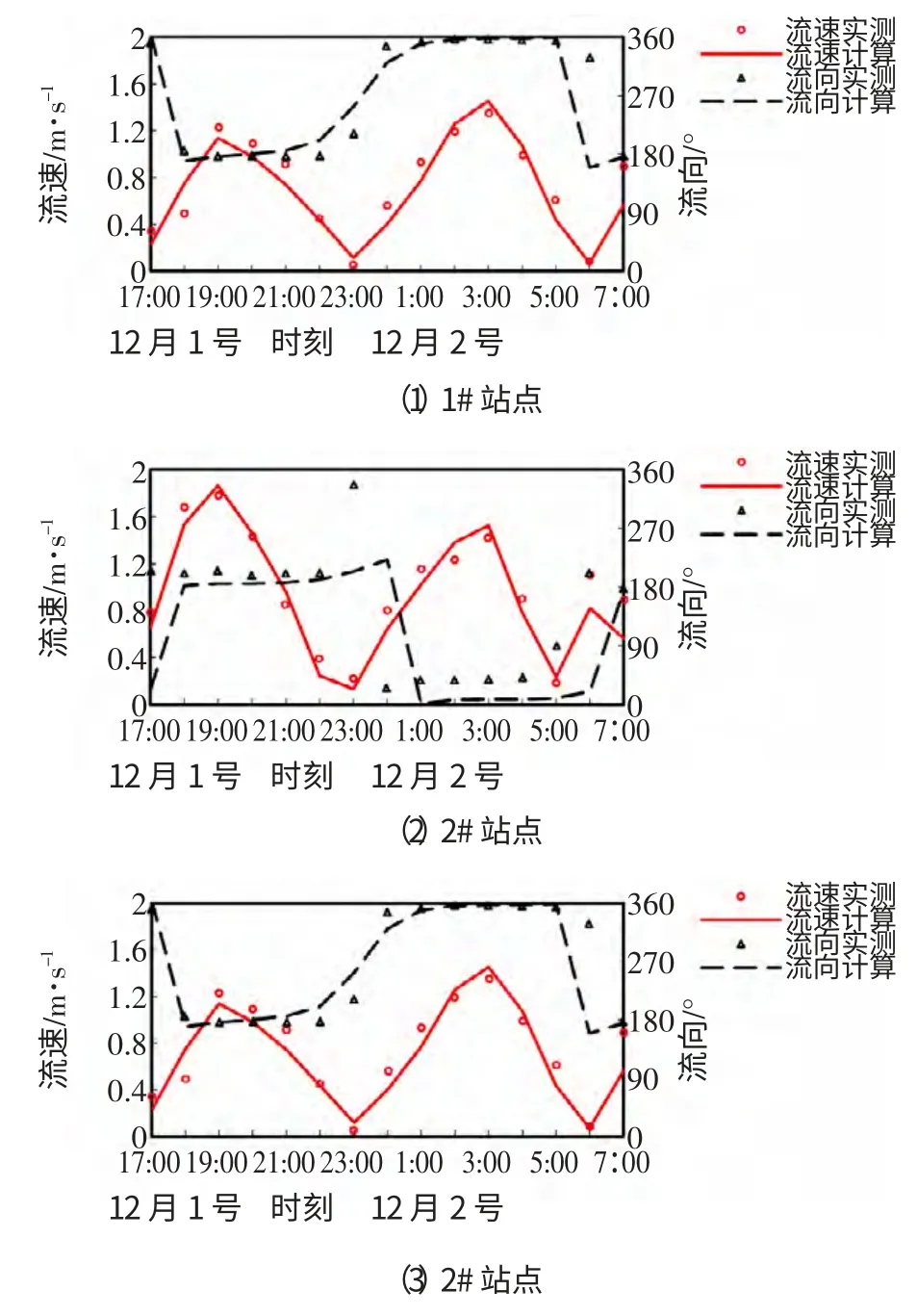
图3 大潮流速流向验证

图4 大潮潮流场

潮流模拟包含大、中、小潮过程，现以模拟潮流场为背景，对辐射沙脊群北部西洋域进行污水输移扩散模拟。依据《江苏省海洋功能区划（2011-2020年）》，从王港口起，沿海洋功能区划排污方向，至7 m 水深处（理论基面，下同） 设为排污位置。本文为了研究不同环境水深对污水输移扩散的影响，同时选取其他两种水深排放位置作为比较。由于5 m 水深以浅往岸近海区，地形复杂多变；而10 m 以深往海区域水深梯度变小，且邻近小阴沙。因而本文从西洋海域王港口排污区向外选取5 m、10 m 两处水深作为比较，以此研究不同环境水深下污水输移扩散的范围及分布规律。a、b、c 为从北往南三处水深位置的编号（图5）。模型初始浓度场设为0，每个排放点污水扩散模拟时段为一个月，计算域内的日均浓度变化在30 个潮周期后达到稳定。当前，在讨论污染物对水域的环境影响时，常采用最大包络的概念，即在水域中某种浓度值可能影响的最大范围。图6 给出了大潮时刻5 m、7 m 和10 m 水深排放位置处污水影响的稀释度最大包络范围图。本文所述的稀释度为污水稀释后水体总体积中所包含的污水体积之比。若以Di表示稀释度，C 表示空间某个位置的污水浓度，C0表示排放的污水源浓度，Ca 表示背景浓度，则空间某个位置的当地稀释度如式（6）

若Ca很小，也可以简化为Di=C0/C。

图5 排放点设置示意图

从图中得到，不同水深处排放的污水在西洋海域潮流的对流和扩散作用下，沿着往复主流向形成南北向长条形状的浓度带。大潮期，3 种水深处排放的污水影响范围均不大，其中10 m 水深处污水500 和200 稀释度等值线包络面积明显小于另外两处水深位置，对水环境造成的影响最小，而5 m 水深的最大。值得注意的是，5 m 排放点群稀释度50、100、200 和500 线均有出现；7 m 点群未出现50 稀释度线；10 m 点群未出现50、100 稀释度等值线。出现上述现象的原因是，5 m 点群位于涨落潮流速较小的浅滩附近，不利于污水的扩散，污水影响范围大；而7 m 与10 m 排放点群水深相对较大，其流速较大，扩散能力强，利于污水的输移扩散。

图6 5、7 和10 m 水深3 个排污位置大潮包络稀释度分布

为了定量说明水深对污水输移扩散影响，表1给出了大潮时期各个排放点的污水扩散稀释度等值线包络面积，图7 为500 和200 大潮稀释度等值线包络面积沿水深的变化过程（坐标轴y 数值为水深点群的平均值）。从表1 和图9 很明显得出水深与污水扩散能力的关系。5 m 和7 m 水深点500 稀释度等值线影响范围较大，但均未侵入浅滩。10 m水深点500 稀释度等值线包络面积远小于前两处水深点。类似地，200 稀释度等值线包络面积也具有随着水深增加呈向外海递减的规律。

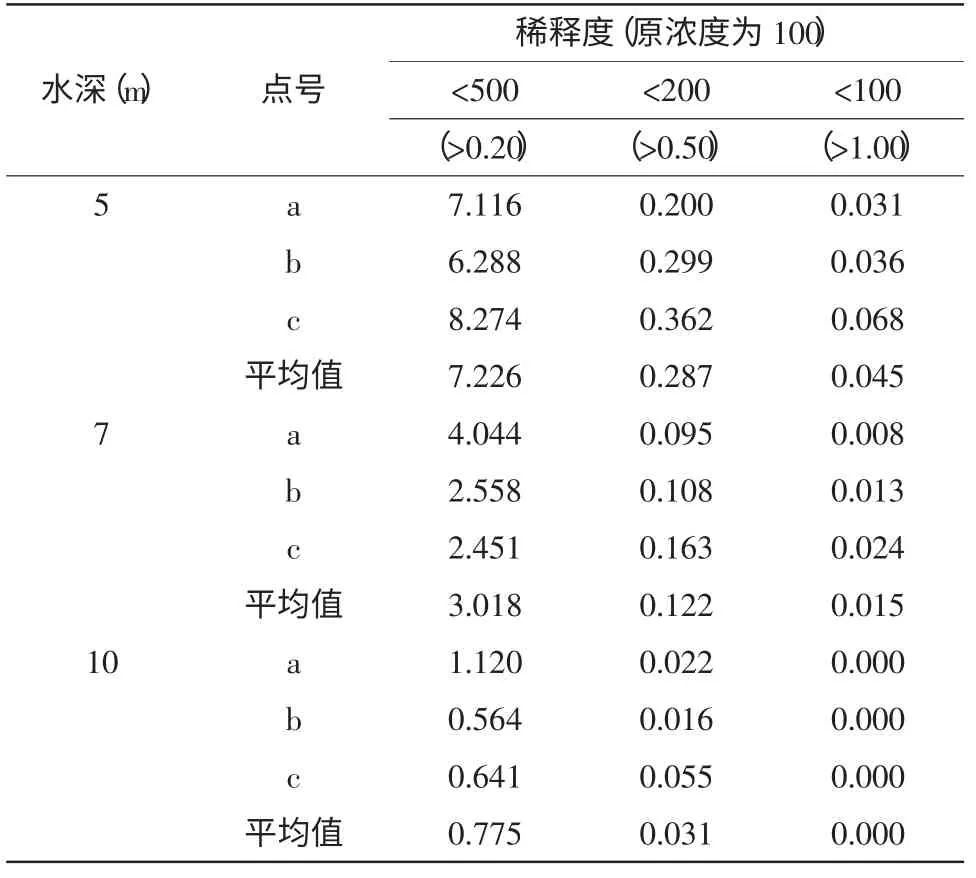
表1 污水扩散稀释度（浓度） 的包络线覆盖面积（km2）

3 不同污水排放量的包络面积

污水排入海域，在相对源强浓度不变的条件下，稀释度等值线包络面积与污水排放量成正比。为了探究它们之间的数值关系，选择7m 水深处b点作为典型排放口，将污水排放量设置为10 万t/d至40 万t/d 每间隔2.5 万t/d 共13 组数据，表2 为同一大潮时期不同污水排放量条件下的500、200稀释度等值线包络面积。基于最小二乘法原理，图8 和图9 给出了两种稀释度情况下污水排放量与包络面积的拟合曲线。可以看出，两种不同稀释度情况的面积与污水排放量幂级数相关性程度较高，拟合优度R2均大于0.99。曲线为凹形说明污水包络面积的增长速率大于排放量的增大速率。值得注意的是当污水日排放量降到15 万t，该海域500 稀释度包络面积小于1 km2，200 稀释度包络面积小于0.1 km2，这与该海域潮流大、自净能力强等水动力特性有关。即污水排放量增大，海域的水动力条件足以在短时间内使污水充分输移扩散。

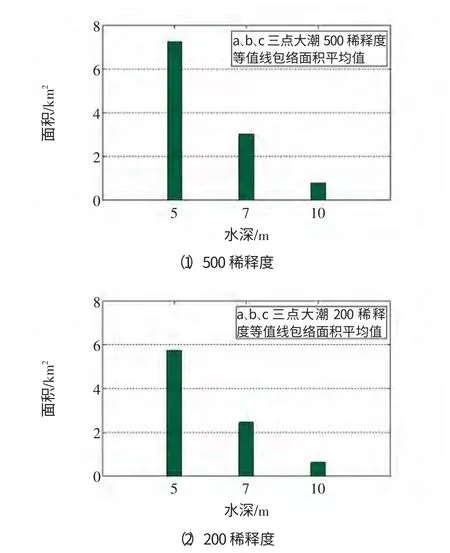
图7 两种稀释度下不同水深包络面积的比较

表2 不同污水排放量对应的包络面积（km2）

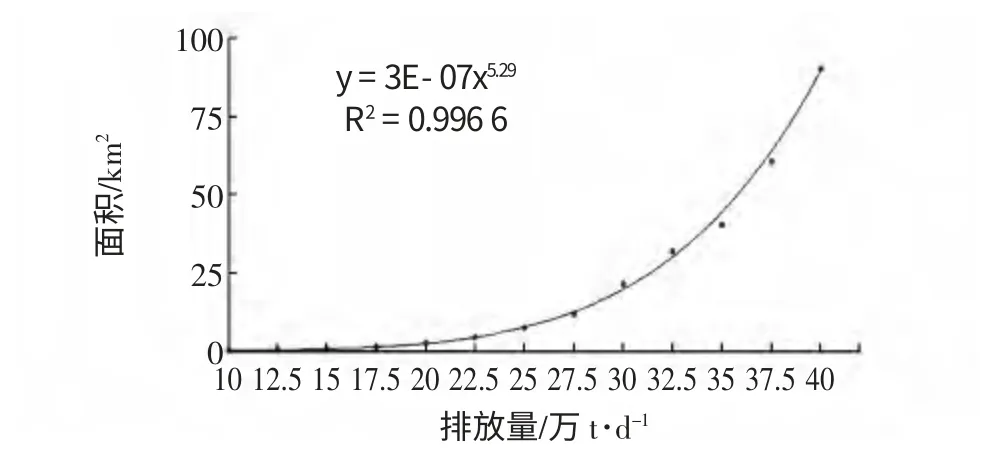
图8 稀释度500 污水排放量与包络面积曲线

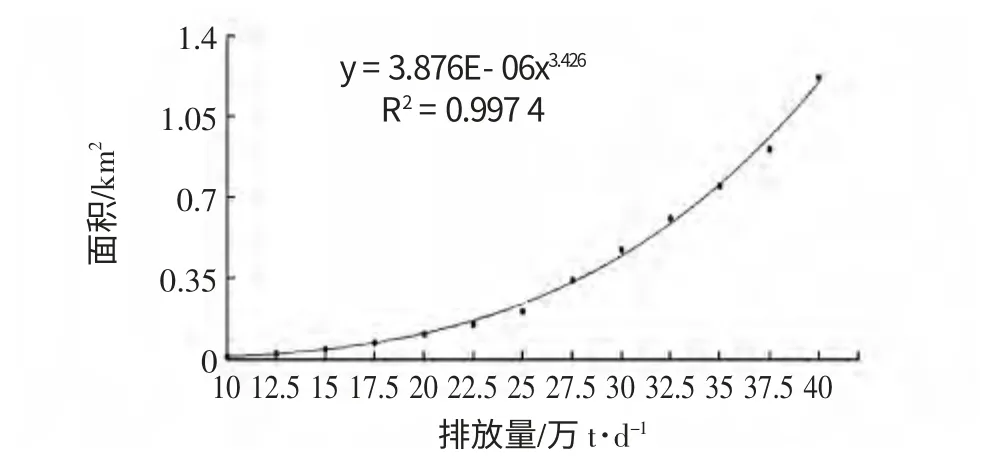
图9 稀释度200 污水排放量与包络面积曲线

4 结语

基于平面二维潮流和物质输移扩散数学模型，模拟了南黄海辐射沙脊群西洋海域的潮流场和污水扩散场，得到了如下的主要结论：

（1） 污水排入海中后，很快被稀释，不同水深处排放的污水200 稀释度等值线大潮包络面积均小于0.5 km2。500 稀释度等值线的面积都小于10 km2，说明污水排入西洋海域不会对海域的水环境产生大的影响。

（2） 环境水深是影响该海域污水扩散稀释能力的主要环境因素，从3 种不同水深排放点的影响范围得出，5 m 点的平均大潮包络面积最大，又位于浅海区，对海洋养殖及生态保护极为不利；7 m 水深点潮流较大，污水包络面积较小。10 m 点位于深水区，流速大，利于污水扩散，排放点排出的污水能被水体快速稀释，因此污水包络面积最小，对海域水环境影响最小。建议在条件允许的条件下，将污水排放位置设置在较大水深处。

（3） 拟合了500 和200 稀释倍数的污水排放量与大潮包络面积的曲线，发现幂级数曲线与计算结果吻合良好，在一定程度上可推算出其他污水排放量下200 和500 稀释倍数大潮包络面积。依据排放量与稀释度包络面积的关系，结合海域的环境容量，可推算该海域的最大污水排放量。

Blumberg A F,Kantha L H, 1985.Open boundary condition for circulation models.Journal of Hydraulic Engineering.111(2):237-253.

ORLANSKI I, 1996. A simple boundary condition for unbounded hyperbolic flow.Journal of Computational Physics.21(3):251-269.

Zhang C K,Zhang D S,Zhang J L,et al,1999.Tidal current-induced recovery-Internation of depositional dynamics of format-ion and evolution of radial sand ridges on the Yellow sea seafloorScience in China(series D),28(5):394-402.

Zhu Y L,Yan Y X,Xue H C,1998.Study on the hydrodyna-mic mechanism of the formation and development of radial sand ridges in the south Yellow Sea-tidal current characteristics. Science in China(series D),28(5):403-410

陈红卫，2011. 促进江苏沿海开发的水资源保护对策. 城镇供水，（6）：79-82.

龚政，张东生，陈永平，2002.陆源污水对连云港海域环境影响研究.海洋工程，20（4）：72-77.

河海大学，1995.浙江三门核电厂可行性研究低放尾水和余氯排放数学模型.

陶建峰，张长宽，2005.黄海辐射沙脊群海域水环境数值模拟研究.河海大学学报：自然科学版，33（4）：472-475.

王颖，2002.黄海陆架辐射沙脊群[M].中国环境科学出版社.

徐凡，陶建峰，张长宽，等，2013.南黄海辐射沙脊群西洋水道质点示踪数值模拟.水道港口，34（2）：94-98.

张东生，张君伦，1996.黄海海底辐射沙洲区的M2 潮波.河海大学学报.（5）：37-42.

诸裕良，2003.南黄海辐射状沙脊群动力特征研究.南京：河海大学博士论文.

朱玉荣，常瑞芳，1997.南黄海辐射沙洲成因的潮流数值模拟解释.青岛海洋大学学报，（2）：218-224.