方变圆的体积计算

陈棽棽，韦迎旭

(河南省电力勘测设计院，河南 郑州 450007)

1 概述

目前由于工程优化及降低造价的要求，在火力发电厂煤仓间内煤斗储煤量满足锅炉最大连续蒸发量工况耗煤小时数符合相关规程的前提下，力争降低煤仓间输煤皮带层的标高以及提高煤斗的充满系数，这样煤斗的形状除了传统的平壁型(图1)、圆锥型(图2)、双曲线渐缩型(图3)等以外，还出现了如方变圆(也称方圆节)型和裤衩腿型等异形煤斗；为了方便、准确地计算这些异形煤斗的几何容积(体积)，有必要明确其理论计算公式。

图1 平壁型

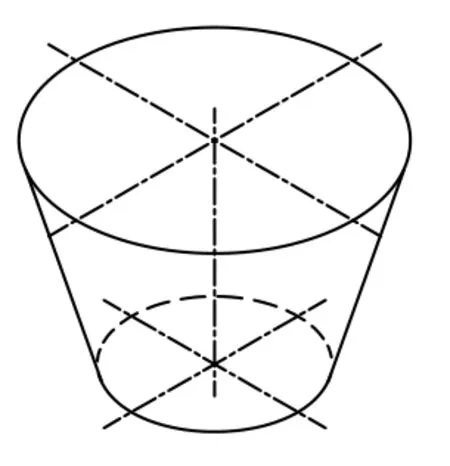
图2 圆锥型

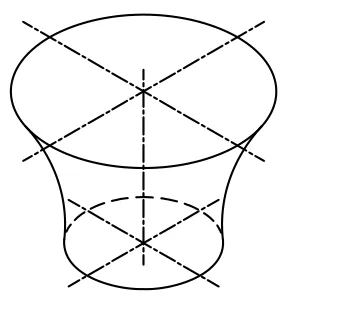
图3 双曲线渐缩型

而方变圆形状几何体的体积在大多数书籍和资料中未列出过其通用的计算公式，本文试图采用数学积分的方法进行推导，从而得出其通用公式。

另外，关于方变圆形状几何体的表面积计算，也是我们所关心的内容。但由于这牵涉到更加复杂的推导和计算，甚至不能用解析式表达出来(涉及椭圆积分)，需要通过计算机数值算法才能得出，笔者将在另文中加以讨论，本文中不再赘述。

2 方变圆几何体的主要尺寸特征值

典型的方变圆几何体见图4。

其矩形端所在的平面与圆形端所在的平面是平行的。

将矩形端的两边长分别用a和b表示，圆形端的半径用R表示，方形端平面与圆形端平面间的距离用h表示。矩形中心与圆形圆心在水平方向上的偏差，即偏心距分别用c和d表示。

图4 方变圆几何体的主要尺寸特征值

3 积分求解方变圆的体积公式推导

首先建立一个三维直角坐标系，为了计算方便，将原点定于圆形端的圆心上，见图5。

图5 三维直角坐标系中的方变圆

设想在Z坐标方向的一定高度z上平行于方变圆上下两端平面截取一个截面s，可以推导出s的形状见图6。

图6 截面s的形状

截面s的截面积S的计算公式见式(1)：

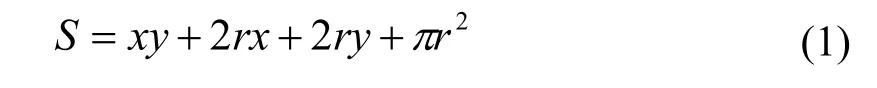
则方变圆的体积V的计算公式为：

式(2)即为方变圆几何体体积的通用理论计算公式，从式中可以看出其体积仅与矩形端和圆形端的几何尺寸以及两端间的距离(即h，也可称为高)有关，而与两端中心的偏心距无关。

4 运用拆解变形方法验证体积公式

祖暅是我国南北朝时期著名数学家祖冲之之子，也是一名杰出的数学家，提出了著名的“祖暅原理”。

祖暅原理，又名等幂等积定理，原文为“幂势既同，则积不容异。”，内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的任何平面所截，如果截得两个截面的面积总是相等，那么这两个几何体的体积相等。

图7 方变圆拆解变形示意图

从祖暅原理的表述中可以看出，其本质也是与数学积分相同的；这就为我们采用拆解变形的方法来验证方变圆体积的计算公式提供了依据。

从图7中可以看出原先的方变圆可拆解为四个部分：(a)、(b)、(c)、(d)，而将其中的(a)、(b)、(c)继续等体积分别变形为(a’)、(b’)、(c’)，则(a’)可形成一个正圆锥，(b’)和(c’)均形成一个三棱锥，而(d)是一个四棱锥。

可以简单地看出，(a’)的体积为πR2h/3，(b’)的体积为bRh/3，(c’)的体积为aRh/3，而(d)的体积为abh/3；而原先的方变圆体积是(a’)、(b’)、(c’)和(d)四部分的总和，这样就与式(2)的结果是完全一致的。

5 结语

通过公式推导，可以得出方变圆几何体的体积公式为：

这也从拆解变形法中得到了验证，从而证明了该式的正确性。

[1]DL/T5145－2002，火力发电厂制粉系统设计计算技术规定[S]．

[2]原北京矿业学院高等数学教研组．数学手册[M]北京：煤炭工业出版社，1976．