含噪ICA模型的一种时频算法

郭 敏， 郭 靖

(1.武汉理工大学 网络信息中心， 武汉 430070； 2.西南大学 电子信息工程学院， 重庆 400715)



含噪ICA模型的一种时频算法

郭 敏1， 郭 靖2*

(1.武汉理工大学 网络信息中心， 武汉 430070； 2.西南大学 电子信息工程学院， 重庆 400715)

实际ICA(Independent Component Analysis)模型中，观测信号常常被各种噪声干扰，致使ICA的源估计相当困难.针对信号源噪声污染情形，分析了ICA模型的估计难点；并假设信号和噪声的时频特性不同，以一种高性能的双线性时频分布计算混合信号的时频特性，辅之Hough空间变换思想，将噪声能量扩展到整个参数空间，只选择信号能量占主导的自项点进行最小二乘对角化估计源信号，提出了一种时频抗噪ICA方法；最后，详细分析了该方法的抗噪性能.该方法扩展了ICA模型的应用限制条件，能有效分离各种非平稳信号.

信号源噪声； RID分布； Hough变换； ICA； SNR

现实世界中，观测信号往往被各种噪声干扰，这些噪声可能是实际传感器的物理噪声，也可能本身作为源信号之一而存在.然而，当噪声存在时，ICA的源估计相当困难[1-2].针对该问题，研究者提出了常用的解决思路和方法：①稀疏编码收缩法(SparseCodeShrinkage，SCS)[3-4]：SCS假设正交ICA变换具有很强的稀疏性，根据这种稀疏性将含噪信号投影到ICA正交基上来实现降噪.但SCS需要假设噪声和信号相互独立，且需要预先估计噪声的方差.②小波滤波法(WaveletFiltering，WF)[5-6]：WF根据信号和噪声的小波系数在不同尺度上具有不同的性质，构造相应规则，在小波平面采用数学方法对含噪信号的小波系数进行处理.WF成功的关键在于如何保持信号的完整信息.③高阶累积量法(Higher-OrderCumulant，HOC)[7-9]：HOC利用方差、偏度、峭度等高阶联合矩描述信号和噪声的分布特征，能避免因高斯噪声带来的问题，缺点是高阶累积量对野值敏感，且计算量大.④极大似然估计方法(MaximumLikelihood，ML)[10-11]：ML是将信号的密度用高斯混合模型的密度来逼近，不过，计算量大.⑤偏差去除技术：(BiasRemovalTechniques，BRT)[12-13]：BRT对无噪的ICA方法进行修正，以去除由于噪声引起的偏差，关键是如何从观测量中获得不受噪声影响的度量标准.

本文假设噪声施加在传感器上的效果可等效为附加源信号的情形，分析了含噪ICA模型的估计难点.在此基础上，假设信号和噪声的时频特性不同，通过把一维时域中的含噪信号映射到二维的时频平面来获取信号的频率特性随时间变化的信息，并映射到Hough变换空间，选择信号能量占主导的自项点进行最小二乘对角化，进而估计源信号，去除噪声，提出一种新的去噪ICA算法.最后以LFM(LinearFrequencyModulation)信号分析了该方法的抗噪性能.

1 数据模型

设有m个混叠信号x(t)=[x1(t)，…，xm(t)]T，每个xi(t)接收到的都是n个源信号s(t)=[s1(t)，…，sn(t)]T发出的线性瞬时混叠,其中，s(t)中有l个源信号s1(t)，…，sl(t)，n-l个加性噪声sl+1(t)，…，sn(t),则

x(t)=As(t)+n(t).

(1)

假设：

(P1)混合是线性时不变瞬时混合，A为m×n维的列满秩阵，且m≥n；

(P2)源信号s1(t)，…，sl(t)是零均值、非平稳、互不相关的随机信号；

(P3)噪声sl+1(t)，…，sn(t)为零均值，独立同分布，且与源信号互不相关；

在上述假设下，可以把噪声sl+1(t)，…，sn(t)当作源信号来建模，即

Rss(t，τ)=E{s(t+τ)s*(t)}=
diag[ρ1(t，τ)，ρ2(t，τ)，…，ρn(t，τ)]，

(2)

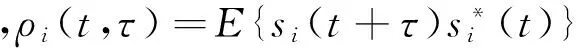
Rxx(t，τ)=E{x(t+τ)x*(t)}=
ARss(t，τ)AH+σ2Im，

(3)

其中，上标H表示共轭转置.设分离矩阵为B，即有B=A-1.由式(1)，有

y(t)=Bx(t)=B(As(t)+n(t))=
s(t)+Bn(t).

(4)

对比分析式(1)、(4)，可知：

1) 由于噪声是源信号之一，则经As(t)后，源信号的结构被噪声破坏；

2)n(t)的存在，进一步破坏了As(t)的结构，分离信号y(t)的各个成分很难保证独立；

3)Bn(t)的存在，输出成分y(t)=s(t)+Bn(t).因此，当噪声存在时，信号ICA估计变得相当困难.

2 ICA时频算法

2.1 白化

由于信号被噪声污染，本文采用子空间的方法来白化观测信号，使得待分离的信号互不相关，协方差矩阵为单位阵I.若对A，有一白化阵W，满足WAAHWH=In.由文献[14]，观测信号x(t)的零延迟自相关阵为：

Rxx(t，0)=ARss(t，0)AH+σ2Im

(5)

则白化阵

(6)

其中，[λ1，…，λm]是Rxx[t，0]降序排列的特征值，[h1，…，hm]为其对应的特征向量.令U=WA，则白化信号为

z(t)=Wx(t)=WAs(t)+Wn(t)=
Us(t)+Wn(t).

(7)

2.2 求白化后信号的RID分布

RID(Reduced Interference Distribution)在抑制交叉干扰项和时频聚集性方面的折衷性较好，其定义为[15]：

(8)

(9)

其中，h(τ)，g(v)分别是时域、频域的对称光滑窗函数.

2.3 Hough变换

Hough变换的本质是对信号进行坐标映射，把平面坐标映射为参数坐标，使映射的结果更易识别和检测.将变换对象由二维函数RIDx(t，v)映射成x(t)的RIDHTx(f0，β)分布，则得到x(t)的RIDHT(RID-Hough Transform)变换[16].设RIDHT的积分直线ABC为：f=f0+βt(f0为截距，β为斜率)，则

(10)

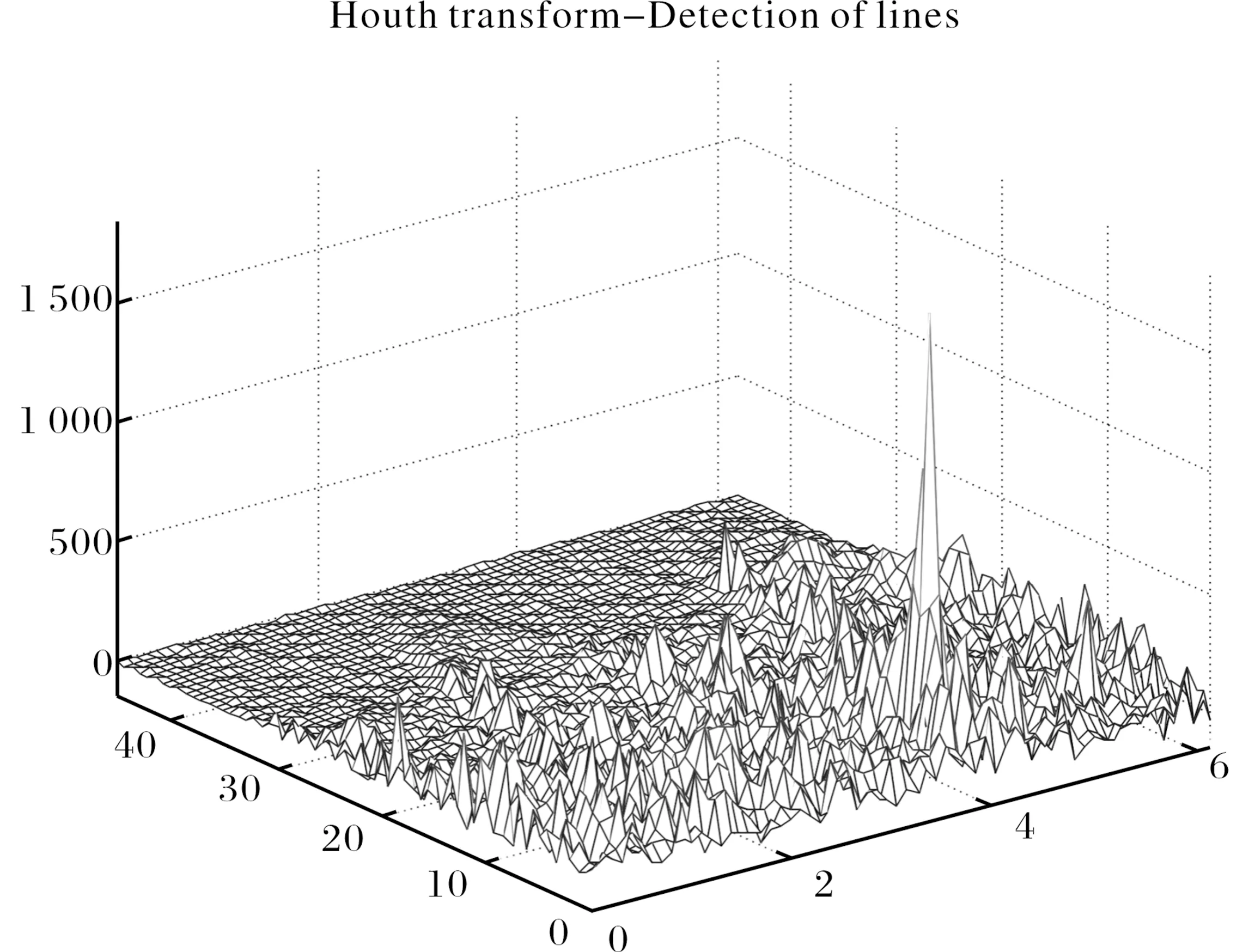
图1 LFM含噪信号的RIDHT分布Fig.1 The RIDHT distribution of noisy LFM signals

2.4 自项点选择

设白化信号的时频谱为Vzz(t，f)，考虑低噪或无噪情况，对式(7)求RIDHT分布

Vzz(f，g)≈WVxx(f，g)WH≈
WAVss(f，g)AHWH≈UVss(f，g)UH.

(11)

根据文献[17]，U为酉矩阵，Vss(f，g)为源信号s(t)的RIDHT分布.对式(11)求特征值运算，有

eig{Vzz}≈eig(UVssUH)≈eig(Vss).

(12)

因此，根据文献[17]求信号z(t)的特征值方法，可得出时频点选择策略：

(13)

其中，ε为[0，1]之间的正数，取ε=0.1.

若信号s(t)在某个平面点(fi，gi)自项Vsksk(fi，gi)≠0，互项Vsksl(fi，gi)=0 (k≠l)，则源信号分布Vss(fi，gi)近似为对角阵.从而，U可采用文献[18]的最小二乘对角化算法求出.

总结上述思路，可得到一种含噪的ICA算法：

1) 对混叠信号零均值化，估计零时延的自相关矩阵Rxx(t，0)；

2) 对Rxx(t，0)进行特征值分解，利用式(6)计算白化阵W；

3) 利用式(10)计算Z(t)的RIDHT变换Vzz(f，β)；

4) 根据式(13)选取自项点；

5) 以最小二乘方法对角化个Vzz(f，β)矩阵，得到酉矩阵U；

3 SNR分析

假定一个LFM信号为:

(14)

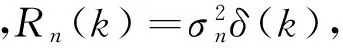
(15)

(16)

若信号x(k)=s(k)+n(k)，对其采样T点，则其RIDHT函数的方差为:

(17)

根据文献[19]，

(18)

因此，输出SNR为:

(19)

由式(19)，可见，信号的输出信噪比取决于源信号的输入信噪比和采样量.进一步简化式(19)，有

(20)

可见，对于含噪LFM信号，如以SNR为评价指标，RIDHT变换所得的输出信噪比SNRout与输入信噪比SNRin和采样数N均成正比.因此，可从提高输入数据的信噪比或/和增加变换的数据量两方面改善ICA算法的性能.

4 实验结果

采用一个EEG(Electroenc Ephalo Graphic)信号(取自The Laboratory for Advanced Brain Signal Processing (ABSP))，和两个高斯白噪声(均值均为0，方差分别为5、25)，采样2048个点.A=[0.1509 0.8600 0.4966; 0.6979 0.8537 0.8998;0.3784 0.5936 0.8216].源信号，观测信号及估计信号分别如图2～图4所示.可见，本文算法能成功估计源信号.

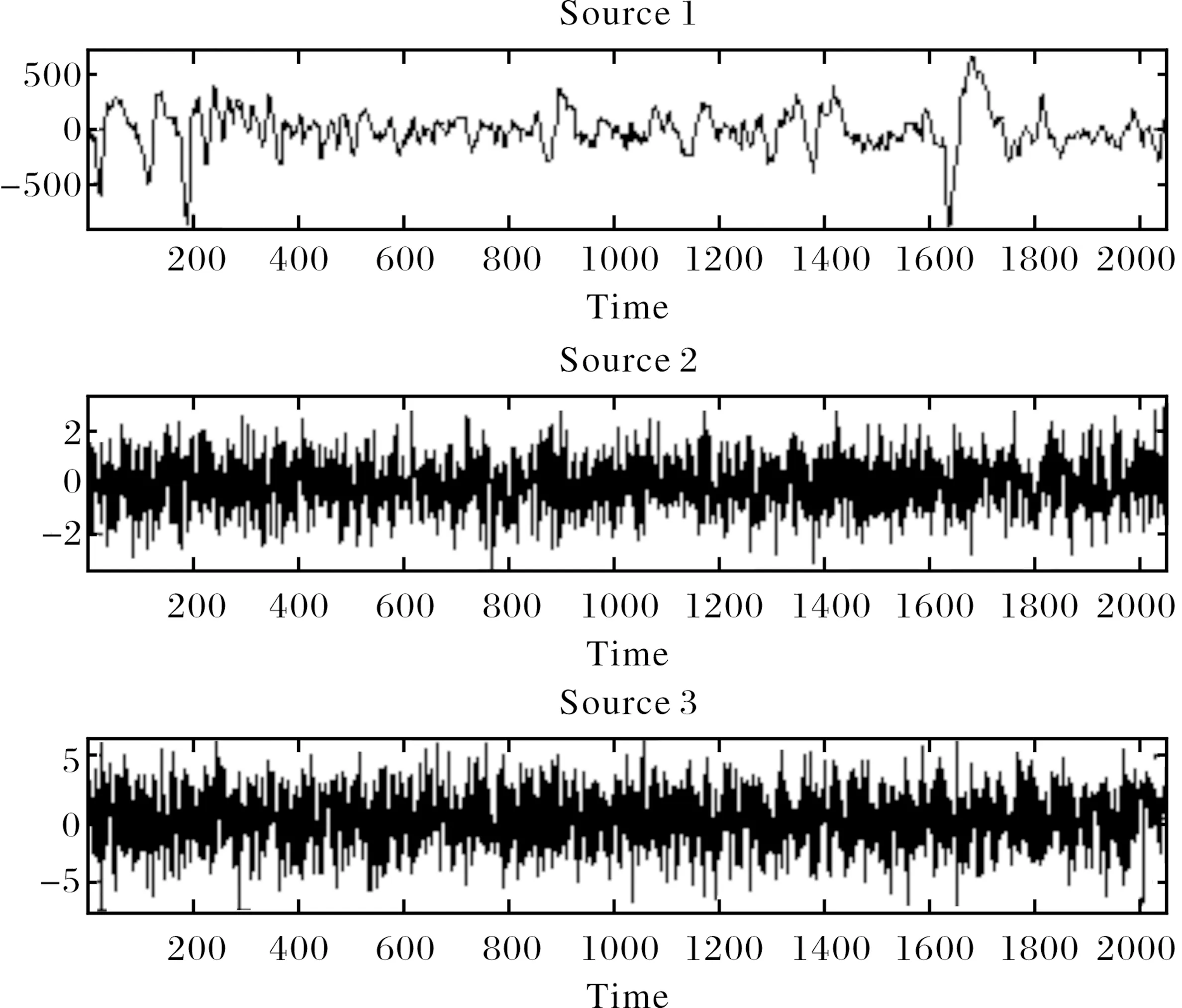
图2 源信号波形图Fig.2 The waveform of sources signals

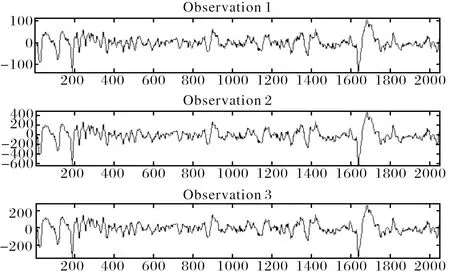
图3 观测信号波形图Fig.3 The waveform of observed signals

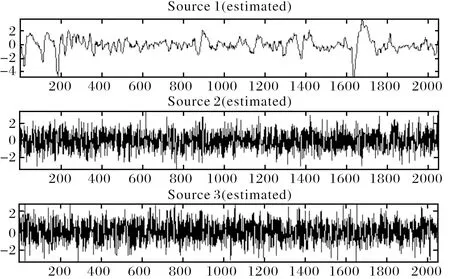
图4 估计信号波形图Fig.4 The waveform of estimated signals

图5显示了不同ICA算法的输出/输入SNR曲线.图6显示了输出SNR和信号采样点的变化曲线.可见，本文算法针对含噪ICA具有更强的抗噪性能，且随着采样数的增加，抗噪性能会更好.

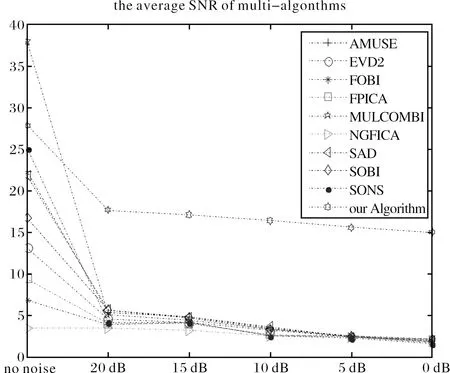
图5 输出/输入SNR变化曲线Fig.5 The curve of output versus input SNR

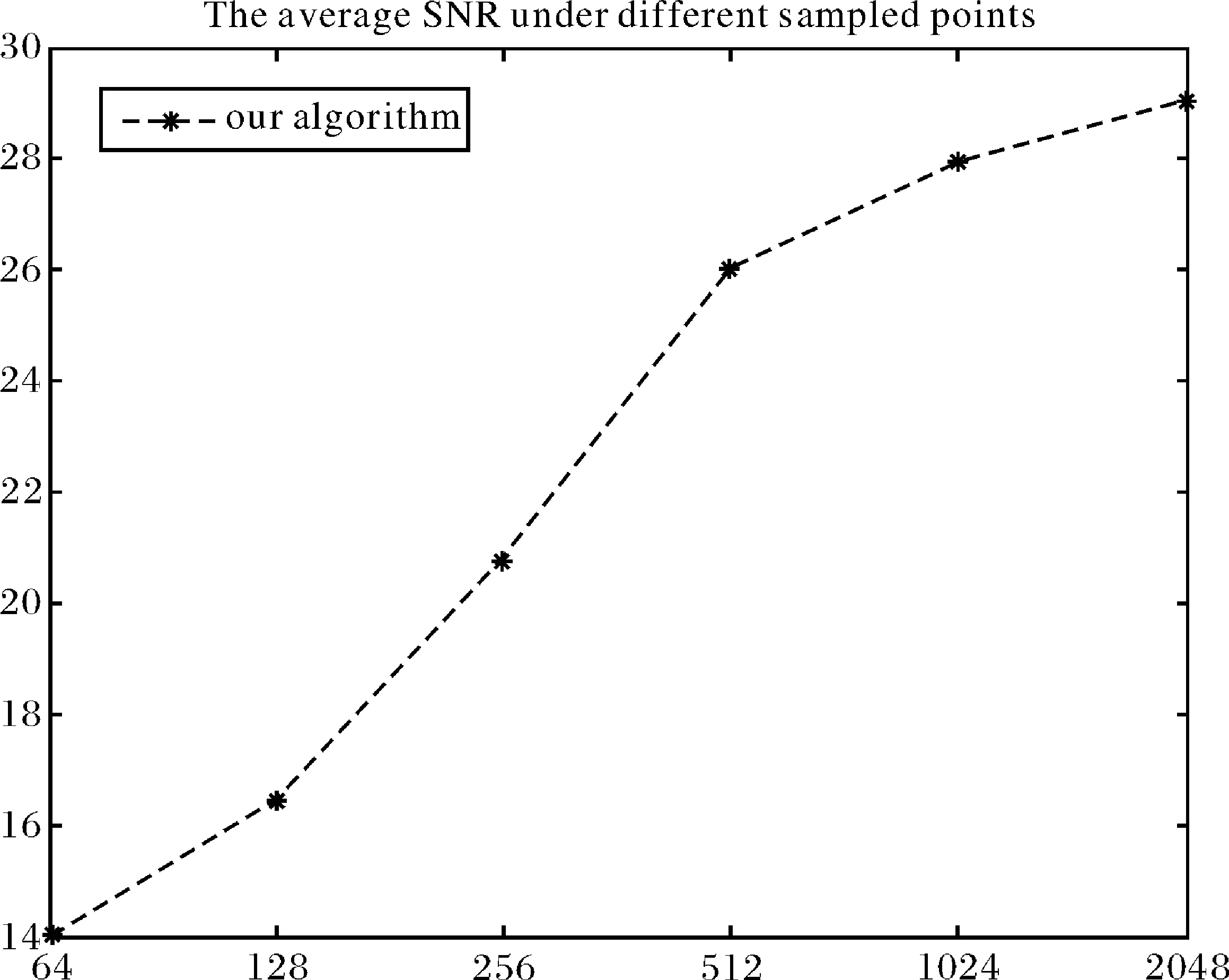
图6 输出SNR和采样点变化曲线Fig.6 The curve of output SNR versus sampling points

5 结束语

本文考虑噪声作为源信号之一的ICA估计问题.研究了含噪ICA信号估计的困难、时频点选择理论、Hough平面映射，提出了一种新的能分离信号源噪声的ICA算法，并分析了该算法的信噪比变化趋势.该算法通过平面变换思想把一维信号转换到二维平面，虽然计算量增大，但拓宽了源信号的限制条件，与基于其他理论的ICA算法相比，不必要求源信号相互独立，或具有稀疏性，只要求源信号的时频谱不同.同时，通过把噪声能量扩展到整个时频面而只选择信号能量占主导的时频点，对噪声具有一定的抑制能力，对野值也不敏感.

[1] 史习智. 盲信号处理: 理论与实践[M].英文版. 上海:上海交通大学出版社， 2011．

[2] 孙守宇. 盲信号处理基础及其应用[M]. 北京: 国防工业出版社， 2010．

[3] Maria J G, Samer A A, Plumbley M D， et al. Sparse coding for convolutive blind audio source separation[J]. Lecture Notes in Computer Science， 2006， 3(1): 132-139．

[4] Phatak K， Jakhade S， Nene A， et al. De-noising of magnetic resonance images using independent component analysis[C]//2011 IEEE Recent Advances in Intelligent Computational Systems， Trivandrum， India， 2011. 807-812．

[5] He Q， Su S， Du R. Separating mixed multi-component signal with an application in mechanical watch movement [J]. Digital Signal Processing， 2008， 18(6): 1013-1028．

[6] Muhammad T A， Wataru M， Christopher J. Employing spatially constrained ICA and wavelet denoising for automatic removal of artifacts from multichannel EEG data journal[J]. Signal Processing， 2012， 92(2): 401-416．

[7] Blanco D， Mulgrew B， Ruiz D P， et al. Independent component analysis in signals with multiplicative noise using fourth-order statistics [J]. Signal Processing， 2007， 87(8):1917-1932．

[8] Karfoul A， Albera L， Birot G. Blind underdetermined mixture identification by joint canonical decomposition of HO cumulants[J]. IEEE Transactions on Signal Processing， 2010， 58(2): 638-649．

[9] Sardouie S H， Albera L， Shamsollahi M B， et al. An efficient Jacobi-like deflationary ICA algorithm: application to EEG denoising[J]. IEEE Signal Processing Letters， 2015， 22(8): 1198-1202．

[10] Li X， Zhong W， Alphones A， et al. Channel equalization in optical OFDM systems using independent component analysis[J]. Journal of Light Wave Technology， 2014， 32(18):3206-3214.

[11] Adali T， Anderson M， Fu G. Diversity in independent component and vector analyses: Identifiably， algorithms， and applications in medical imaging[J]. IEEE Signal Processing Magazine， 2014， 31(3):18-33．

[12] Tang H， Wang S. Noisy blind source separation based on adaptive noise removal[C]//10th World Congress on Intelligent Control and Automation， Beijing， China， 2012: 4255-4257．

[13] Takahashi Y， Takatani T， Osako K， et al. Blind spatial subtraction array for speech enhancement in noisy environment[J]. IEEE Transactions on Audio， Speech and Language Processing， 2009， 17(4): 650-664．

[14] Holobar A， Févotte C， Doncarli C， et al. Single auto-terms selection for blind source separation in time-frequency plane[C]//Proceedings of 11th European Signal Processing Conference， Toulouse， France， 2002: 565-568．

[15] Jeong J， Williams W J. Kernel design for reduced interference distributions [J]. IEEE Transactions on Signal Processing， 1992， 40(2):402-412．

[16] Chau C P， Siu W C. Adaptive dual-point Hough transform for object recognition[J]. Computer Vision and Image Understanding， 2004， 96(1):1-16．

[17] Févotte C， Doncarli C. Two contributions to blind source separation using time-frequency distributions[J]. IEEE Signal Processing Letters， 2004， 11(3):386-389．

[18] Fadaili El M， Thirion-Moreau N， Moreau E. Non-orthogonal joint diagonalization/zero diagonalization for source separation based on time-frequency distributions[J]. IEEE Trans Signal Process， 2007， 55 (5):1673-1687．

[19] 边海龙. 非平稳信号联合时频分析方法的若干问题研究与应用[D]. 成都：电子科技大学， 2008．

A time-frequency algorithm for noisy ICA model

GUO Min1， GUO Jing2

(1.Network & Information Center， Wuhan University of Technology， Wuhan 430070;2.College of Electronics and Information Engineering， Southwest University， Chongqing 400715)

The estimation of signals in ICA (Independent Component Analysis) application model will become a problem because of noise disturbance. In this paper， the problem of noisy ICA model is analyzed against contaminated sources， and a new ICA method is proposed exploiting the difference in the time-frequency signatures of noisy sources to be separated. The approach is developed by firstly using high-resolution time-frequency distributions to obtain signal time-frequency features， secondly localizing the signal energy in parameter space by Hough transform and finally a least squares diagonalization of a combined set of TFD matrices chosen by auto-terms selection method to estimate the source signals. Its performance is also exhaustively derived. This approach extends the ICA application constraints and can effectively separates the various non-stationary sources．

noisy source; reduced interference distribution; Hough transform; independent Component Analysis; SNR

2015-02-27.

国家自然科学基金项目(61205088, 61472330);中央高校业务基金项目(XDJK2014C015);西南大学博士基金项目(SWU112056)．

1000-1190(2015)04-0515-05

TN911.7< class="emphasis_bold">文献标识码： A

A

*通讯联系人. E-mail: poem24@163.com.