一类值得重视的代数运算应用题——从一道中考模考试题说起

☉江苏省如皋市九华镇九华初级中学 夏建明

一类值得重视的代数运算应用题
——从一道中考模考试题说起

☉江苏省如皋市九华镇九华初级中学 夏建明

应用能力是各级考试重点考查的能力之一，特别是代数应用问题几乎在每份中考试卷都会涉及，然而反复检索近年来的中考试卷，却较少发现考查以代数运算为主的应用问题，后来笔者在2015年一批模考试题中竟然有所发现，本文就从这道模考试题说起，并通过对人教版教材的研习、检索，引起各级命题者对这类代数运算应用题的关注．

一、由一道模考题说起

题目如图1，“丰收1号”小麦的试验田是边长为am（a＞1）的正方形去掉一个边长为1m的正方形蓄水池后余下的部分，“丰收2号”小麦的试验田是边长为（a-1）m的正方形，两块试验田的小麦都收获了500kg．

图1

（1）用含a的式子表示两块试验田的单位面积产量.

（2）哪种小麦的单位面积产量高？（请给出必要的演算或说明）

（3）当a＝26时，高的单位面积产量是低的单位面积产量的多少倍？

思路简述：（1）“丰收1号”试验田的面积为（a2-1）m2，它的单位面积产量为kg/m2；“丰收2号”试验田的面积为（a-1）2m2，它的单位面积产量为kg/m2.

（2）（a2-1）-（a-1）2＝2a-2＝2（a-1）．由题意a＞1，所以2（a-1）＞0.所以（a2-1）＞（a-1）2．所以．即“丰收2号”的单位面积产量高．（说明：如果学生直接观察图形，从图形面积的角度解释（a2-1）＞（a-1）2，我们认为也是可以的）

研习教材：这道考题的原型来自人教版八上教材第136页，分式乘除运算的一道例题，从上面求解来看，主要涉及分式的列式、分式的乘除运算与化简，同时还涉及作差法比较两式大小．对分式及其运算的考查比较到位，有着较好的区分度．

沿着这种应用问题的角度再读教材，我们有了很多新的发现，原来教材上这类代数运算的应用问题还有很多，下面列举几题．

二、教材上代数运算应用问题例举

教材习题（人教八上教材第125页，第12题）某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：

（1）第一次提价p%，第二次提价q%；

新课改初期，针对很多数学教师对新课程的困惑，我们将教研内容的重点放在了课堂教学上，教研活动以集体备课、公开课、研磨试题为主。定期开展包括教材分析研究、复习备考研讨等主题在内的多层次、多角度的备课活动，定期开展基于新课程理念的课堂教学交流、研讨等教研活动。区域教研组的公开课主要分为骨干教师的示范课和青年教师的展示课。青年教师的展示课多以同课异构、跨校上课的形式进行，并由专家、优秀教师现场指导。每个模块的教学结束后进行统一测评，并组织研磨试题活动。

（2）第一次提价q%，第二次提价p%；

其中p，q是不相等的正数．三种方案哪种提价最多？

思路简述：设原料的原价是m元，p%＝a，q%＝b.

方案一：m（1＋p%）（1＋q%）＝m（1＋a）（1+b）=m（1＋a＋b＋ab）.

方案二：m（1＋q%）（1＋p%）＝m（1＋b）（1＋a）=m（1＋a＋b＋ab）.

显然，方案一、二提价相等，需要比较方案三与前者的大小，运用作差法比较如下：

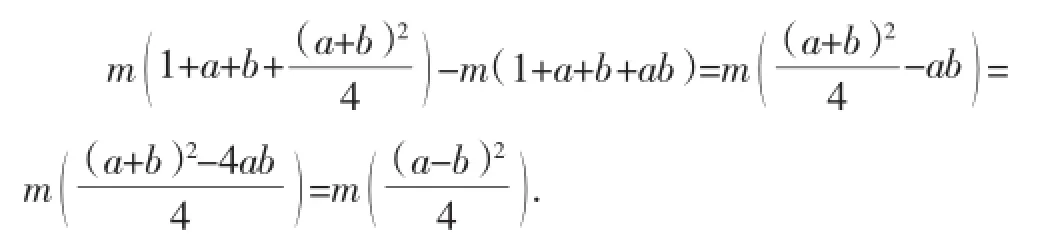
三、对命题取向和解题教学的启示

可以发现仅八年级上册教材在整式乘除运算、分式运算内容中，只在例题或习题的“拓广探索”的最后一题安排了两次涉及代数运算类型的应用问题，而且这两章代数内容也应该是初中数学的核心内容之一，那么在各级命题中理应有这类应用问题的一席之地．以下围绕相关话题提出一些操作性建议：

1.降低起点，从特例出发推广到一般

由于以上提及的教材习题安排在“拓广探索”栏目，教材编写者可能是让学有余力的学生挑战这类问题，根据我们的教学经验，数学适应性不好的学生难以接受这类问题，过于抽象、晦涩，读不懂题意，作为命题研究，为了追求更多考生参与、理解这类问题，建议先安排特例引路，比如，对于教材习题，我们可以先给出一些特殊值让更多的学生理解.

特例引路：某种产品的原料提价，因而厂家决定对原定价为100元的产品提价，现有三种方案：

方案一：第一次提价10%，第二次提价30%；

方案二：第一次提价30%，第二次提价10%；

方案三：第一、二次均提价20%．

三种方案中哪种提价最多？

简评：相信经过特例引路，应该有更多基础不好的学生能动手练习，而优秀考生也可以借助于特例引路增加对问题的理解，然后再过渡到抽象的一般表示，让他们感受到数学中从特殊到一般的思想方法．此外，在目前很多地区仍然是大班教学的前提下，学生的水平参差不齐，要想取得较好的教学效果，增设特例引路可能是较为现实的途径．

2.挖掘教材资源，编拟代数运算应用问题

如“模考题”一样，其实源自教材例题，“题干”并没有改变，只是下设的三个小问与教材上的两个问题相比，梯度更加明显，让更多学生能参与进来，让学生感受到分式运算的解释力量．由此受到启发，我们在七年级命题时，曾改编一道教材例题，也追求了从特殊到一般的命题取向.

教材探究：（人教版七上，第102页，销售中的盈亏）一商店在某一时间以每件60元的价值卖两件衣服，其中一件盈利25%，另一件亏损25%，那么卖这两件衣服总的是盈利还是亏损，或是不盈不亏？

改编设问，得到下列一系列变式问题：

变式1：某服装店在某一时间以每件100元的价格卖出两件服装，其中一件盈利25%，另一件亏损25%，那么卖这两件衣服总的是盈利还是亏损，或是不盈不亏？

变式2：某服装店在某一时间以每件a元的价格卖出两件服装，其中一件盈利25%，另一件亏损25%，那么卖这两件衣服总的是盈利还是亏损，或是不盈不亏？

变式3：某服装店在某一时间以每件100元的价格卖出两件服装，其中一件盈利25%，另一件亏损20%，那么卖这两件衣服总的是盈利还是亏损，或是不盈不亏？

变式4：某服装店在某一时间以每件a元的价格卖出两件服装，其中一件盈利25%，另一件亏损10%，那么卖这两件衣服总的是盈利还是亏损，或是不盈不亏？

改编意图：变式1、变式2的目的是让学生经过特值引路过渡到这类问题的一般结构；而变式3、变式4则是为了纠正学生容易形成的思维定势，让他们养成具体问题具体分析的好习惯．

四、写在最后

数学命题研究博大精深，既需要一定的解题能力，特别是命题者本身在解题之后对问题深层结构的揭示与洞察，又需要对所教数学的深刻理解，包括对本学段数学知识的学段特征有清晰的认知，还需要对大样本下学生整体数学认知水平的精准研判等．具体到本文关注的这类代数运算应用问题，则是一类值得重视的命题方向，因为它反映了数学中从特殊到一般的学科特点，能让数学适应性优秀的学生感受到数学思维的彻底性，通过数式运算解释的力量感．想来，研习教材、理解教材并不是很简单的吧．

1.刘东升．经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］．中学数学（下），2014（4）.

2.刘东升．重视教材“活动材料”，追求变式教学效率——以一道中考模拟卷压轴题为例［J］．中学数学（下），2015（6）.

3.刘东升．“以课本为本”：谁解其中味［J］．中小数学，2013（1-2）.

4.章建跃．理解数学是教好数学的前提［J］．数学通报，2015（1）．

5.严冬梅．命题到底该怎样考查概念——以七年级上学期一些习题为例［J］．中学数学（下），2015（3）．

6.仲进东．例谈客观题型中“把关题”的呈现方式［J］．中学数学（下），2015（3）．H