非连续连接的拼合钢柱受力性能试验研究

李 杰 李 强 孙 浩 张丁然 王涤平

(1．同济大学建筑工程系，上海200092;2．上海美申环境设施设备有限公司，上海201712)

1 引言

移动箱体建筑是以集装箱尺寸为模数，在工厂完成建筑和结构建造，便捷运至现场快速装配施工的一种新型建筑体系。箱体的主体结构由四根立柱和顶底两层各四根钢梁组成。同层箱体的装配会出现两根、三根或四根箱体柱子拼合的情况。如何将单独受力的柱子相互结合使其共同受力，借此提高柱子的承载和变形能力是本课题研究的目的。本文通过两根冷弯方管拼合钢柱的轴心受压及偏心受压试验，得到拼合钢柱的破坏模式、截面应变分布规律和基本受力特性。

2 拼合型钢柱研究现状

武胜和张素梅［1］应用冷弯Σ形截面构件两两组合点焊，形成翼缘对焊箱形组合截面和翼缘叠焊箱形组合截面。采用非线性有限元分析得到了这两类轴压构件的变形、屈曲模式和荷载－位移曲线等，计算表明其极限承载力和初始模量大幅提高。

刘向斌和周天华［2］对由C形冷弯薄壁型钢通过自攻螺钉拼合而成的三肢拼合截面立柱进行了有限元研究，分析结果表明随长细比增大，拼合立柱轴压极限承载力降低;螺钉连接间距在一定范围内对拼合立柱轴压极限承载力和刚度的影响不大。

聂少锋和周天华［3］对C形冷弯薄壁型钢四肢拼合截面立柱的轴压试件进行数值模拟，提出了冷弯薄壁型钢四肢拼合截面立柱轴压承载力的设计方法，并将试验值与有限元及各规范公式计算值进行了对比。

聂少锋和周天华［4］对17根由C形和U形冷弯薄壁型钢拼合箱形截面立柱的轴压性能进行试验研究，得到了各试件荷载－位移曲线和破坏特征，并将试验结果与《冷弯薄壁型钢结构技术规范》(GB 50018—2002)(以下简称《薄壁钢规》)的“有效宽厚比法”和《北美冷弯薄壁型钢结构设计规范》(NAS AISI 2007)的“直接强度法”、“有效截面法”的计算结果进行对比分析。

赵一婕和杜兆宇［5］对冷弯薄壁C形钢四肢组合箱形截面受弯构件进行了承载力试验及有限元分析，得到构件的破坏模式、极限承载力和荷载－挠度曲线。提出了实用的折减系数法。

周绪红和李拮［6］对各国有关冷弯薄壁型钢拼合截面柱的轴压试验进行了有限元模拟。分析了构件截面形式、截面尺寸以及长细比对拼合截面柱拼合效应的影响，提出了冷弯薄壁型钢拼合截面柱轴压承载力的简化计算方法。

上述研究的拼合柱截面形式由薄壁Σ形、C形和U形组成，受力形式为轴压及受弯，对于本文设计的由冷弯薄壁方管组合而成的拼合钢柱尚未有研究报道。

3 拼合钢柱试验研究

3．1 试件设计

拼合柱由两根120 mm×120 mm×5 mm的冷弯方管组合而成，钢管材料为Q235。两根试件编号分别为 C—A—29，C—E—29，其中，C代表柱，A代表轴压，E代表偏压，29代表柱高为2．9 m，偏心受压试验的偏心距e取65mm，相对偏心率为0．25。钢柱的材性试验结果见表1，包括弹性模量E、名义屈服强度fy、极限强度fu、延伸率δ及相应平均值。

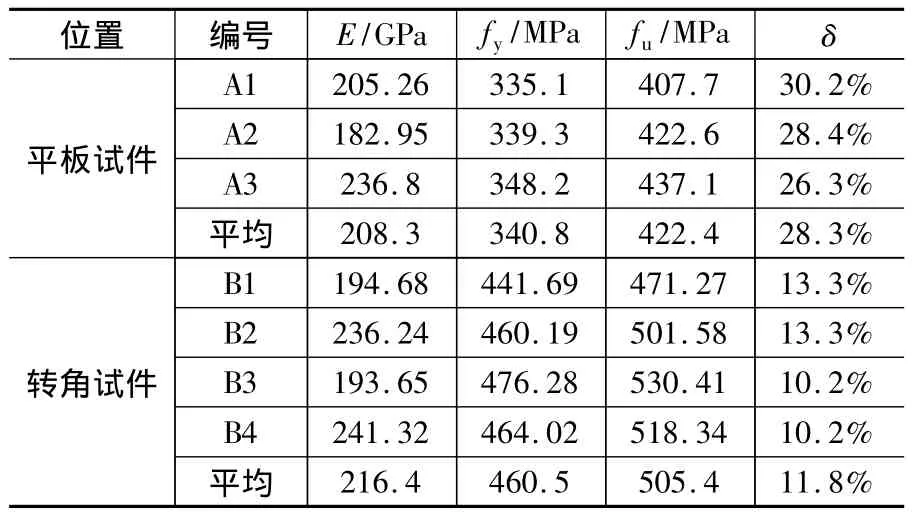
表1 材性试验结果Table 1 The mechanical properties

3．1．1 柱端连接件

移动箱体建筑上下层柱子的连接采用“套管式”连接件，见图1(a)。安装时套管分别插入上下层箱体的柱子从而将箱体连成一体。试验模拟实际情况采用单侧套管柱端连接件，安装时将套管插入柱内，从外侧用螺栓拧紧，见图1(b)。

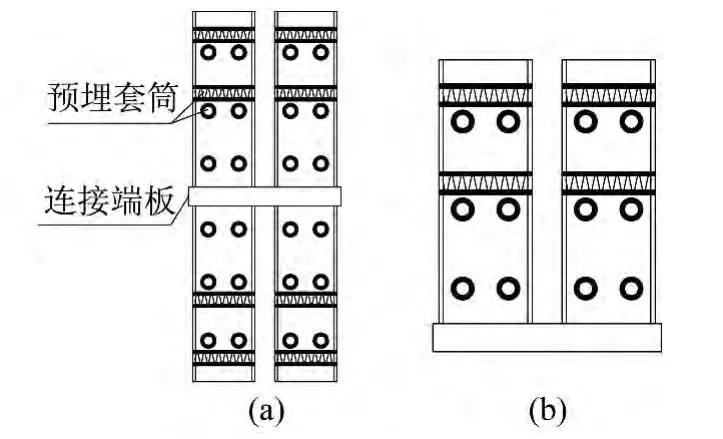
图1 柱端连接件图Fig．1 Connector in the column ends

3．1．2 柱间连接件

本文设计的柱间连接件由四个预先焊接在柱上的阶梯型组件和一个工字插件组成。柱间五个连接件沿柱高从上到下依次编号为J1，J2，J3，J4，J5。连接件尺寸及定位见图2。

阶梯型组件三面围焊于钢柱上，焊脚尺寸为5mm。连接件的抗剪强度由焊缝或工字形插件腹板抗剪中的较小值控制，计算连接件的抗剪承载力:

Nv——连接件抗剪强度;

βf——正面角焊缝的强度设计值增大系数;

he——角焊缝的计算厚度;

lw——角焊缝的计算长度;

b——工字形插件腹板厚度;

l——工字形插件长度;

fv——钢材的抗剪强度设计值。

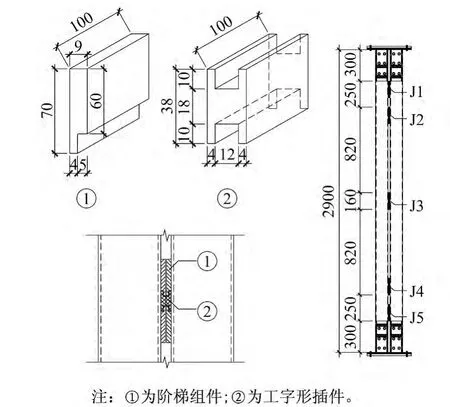
图2 连接件示意图及布置图(单位:mm)Fig．2 Connector between the columns(Unit:mm)

因钢柱受压时，剪力分布为支座处剪力最大，柱中截面剪力为零，故支座处连接件间距较小，柱中连接件则可有效抵抗左、右钢柱的分离趋势。根据《钢结构设计规范》(GB 50017—2003)(以下简称《钢规》)5．1．6 条，构件计算剪力为

故选取一半试件进行分析，共计2．5个柱间连接件需承受剪力为

连接件满足抗剪要求。

3．2 试验装置设计

试验采用单向刀口铰支座，能沿截面强轴方向转动。为防止构件的平面外失稳破坏，在柱子上下三分之一高度处各增加两道侧向支撑，见图4、图5。

3．3 测点布置

在试件柱中截面和两端布置位移计，分别用于观测试件的轴向压缩位移、试件上下两端的水平位移和试件柱中截面水平位移。沿试件高度选取四个截面布置应变片，应变片沿柱高竖向黏贴。测点布置位置及应变片布置方式如图3所示。

由于铁路线路呈长带状，这种GPR探测测线的布设导致每条测线都很长且勘探所获数据量巨大，与GPR探测配套的专业数据处理与解释软件例如常见的RADAN7等，往往需要对每条测线分段进行数据处理和翻浆冒泥病害的人机交互解释圈定，尤其是各个翻浆冒泥病害区域底界控制点的标定，根本无法按比例尺沿铁路正线进行狭长带状区域翻浆冒泥病害底界深度等值线图的绘制。有鉴如此，本论文结合RADAN7和Surfer软件，提出了一种用于GPR勘探的铁路翻浆冒泥病害底界的等值线图绘制方法。

3．4 加载方案

3．4．1 轴心受压柱加载制度

油压千斤顶加载，在预估极限承载力的50%前每级荷载增量100 kN，在预估极限承载力的50%～80%之间每级荷载增量50 kN，之后每级荷载增量20 kN，在构件临近破坏时每级荷载增量10 kN直至破坏。

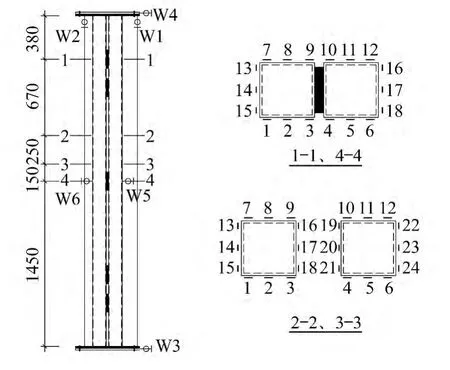
图3 测点布置图(单位:mm)Fig．3 Measuring points(Unit:mm)

3．4．2 偏心受压柱加载制度

在预估极限承载力的50%前每级荷载增量50 kN，在预估极限承载力的50% ～80%之间每级荷载增量20 kN，之后每级荷载增量10 kN直至试件破坏。

3．5 试验过程

3．5．1 轴心受压试验过程

加载初期，连接件位置处的缝隙逐渐变小，柱无弯曲迹象。当荷载加至700 kN时两柱间缝隙略有变大，柱轴向位移约2．13 mm，柱中 W5和W6位移计平均水平位移约0．49 mm;当荷载加至900 kN时，构件出现整体微小弯曲现象，此时柱轴向位移约 2．88 mm，柱中平均水平位移约1．01 mm，构件表面无局部失稳迹象;最终当荷载加至1 318 kN时，构件发生整体失稳破坏，此时柱子轴向位移约 8．46 mm，平均水平位移约12．64 mm。试件最终破坏位置出现在截面2—2与截面3—3之间，破坏形态为其中右侧内凹柱子首先发生局部破坏，进而引起试件整体破坏(图4)。连接件(包括焊缝)未发生任何破坏，但工字插件在卡槽内被夹紧，后期试件顶部的工字插件J1可以较轻松取出，其余四个均难以取出。

3．5．2 偏心受压试验过程

图4 轴心受压试验破坏形态Fig．4 Specimen failure mode under axial compression test

图5 偏心受压试验破坏形态Fig．5 Specimen failure mode under eccentric compression test

3．6试验结果与分析

3．6．1 荷载－竖向位移曲线

图6所示为轴压和偏压试件的竖向荷载和竖向位移曲线，轴压竖向位移取W1和W2的平均值，偏压由于W2失效，故采用W1数据。图中可见，加载初期，荷载－竖向位移曲线基本呈线性关系，随着荷载增大，逐渐呈曲线变化，刚度下降;达到极限荷载后，曲线下降，轴向位移迅速增加，试件发生破坏。对比两条曲线可见轴压试件承载力高于偏压试件，前者为后者的1．55倍;轴压试件的极限变形比偏压试件小，前者为后者的0．53倍;耗能能力前者为后者的0．921倍。由此可见，随着偏心距增大，竖向承载力降低，变形能力增加。

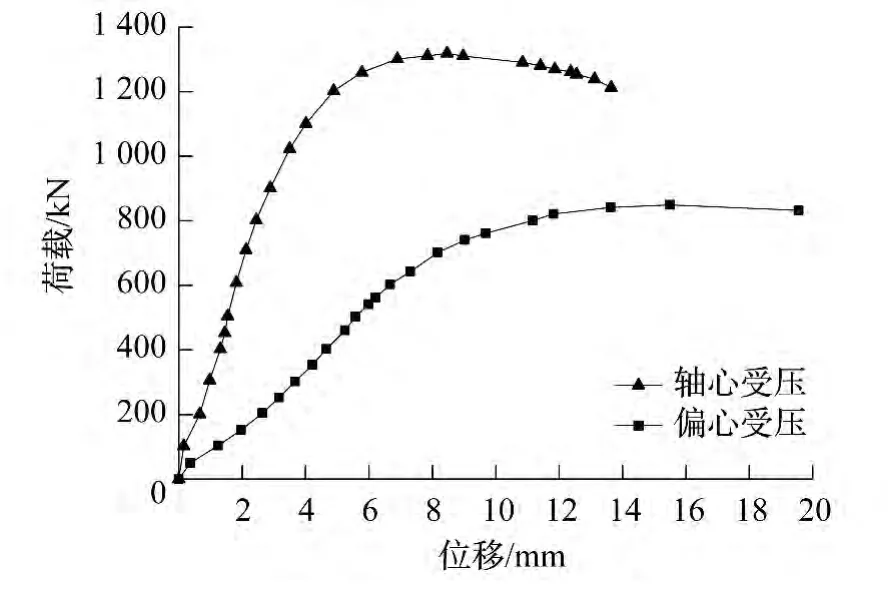
图6 荷载－竖向位移曲线Fig．6 Load-vertical displacement curves

3．6．2 荷载－水平位移曲线

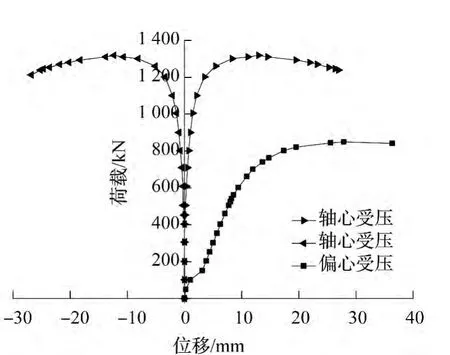
图7 荷载－水平位移曲线Fig．7 Load-horizontal displacement curves

试件荷载－柱中截面水平位移曲线如图7所示，轴压水平位移取W5和W6的平均值，偏压由于W5失效，故采用W6数据。由图可见，轴压柱初始荷载－水平位移曲线沿y轴上升，说明柱子处于较为理想的轴心受压状态。当加载到约500 kN时两曲线产生分离，说明构件产生微小弯曲。随着荷载的增加，侧向位移逐渐增大，曲线表现出极值点失稳的特征。对偏压柱，起初曲线水平位移不大，当荷载达到100 kN时，柱中截面水平位移突然加大，之后位移发展较快。对比图中右侧两条曲线可见，偏压荷载－柱中截面水平位移曲线较为平缓;极限荷载时轴压试件的柱中截面极限变形比偏压试件小，前者为后者的0．482倍。对于偏压柱，由于附加弯矩影响，随荷载增大，柱中出现明显的弯曲，当加至极限荷载后，荷载开始缓慢下降，柱中变形则快速发展，试件破坏。

3．6．3 荷载应变关系

将不同荷载作用下，各截面正应变分布情况归纳如表2及表3所示，图中内侧表示受拉，外侧表示受压。

表2 轴心受压时不同荷载作用下各截面正应变分布情况Table 2 Normal strain distributions under axial compression test

由表2可知，4个截面的应变变化情况大致相同。当荷载为0．30Pu(400 kN)时，图示4个截面的应变分布基本一致，左右柱截面的应变分布也大致相同;当荷载达到0．46Pu(600 kN)时，4个截面的应变分布仍然差别不大，但试件偏心受力趋于明显，发生局部失稳的右柱截面应力较左柱截面应力稍大，并出现不均匀增长;当荷载为0．98Pu(1300 kN)时，4个截面左右柱各边的平均应变为940～4 829 με，除2—2、3—3、4—4 截面处左柱左侧腹板平均应变小于屈服应变1 619 με外，其他各边平均应变均已超过了屈服应变，试件趋于破坏。

由表3可知，1—1截面及4—4截面由于连接件局部刚度突变的缘故，导致截面受力复杂，出现应力集中现象，而2—2截面及3—3截面的应变较符合平截面假定。当荷载为0．35Pu(300 kN)时，4个截面的应变分布基本一致，靠近荷载作用点的右方钢管截面应变明显较大;当荷载达到0．59Pu(500 kN)时，4个截面的应变分布仍然差别不大，且试件右柱右侧腹板平均应变均未超过屈服应变;当荷载为0．94Pu(800 kN)时，试件4个截面处右柱右侧腹板的平均应变(3 085～4 816 με)均已远远超过了屈服应变，但试件左柱左侧腹板的平均应变(525～1 206 με)仍处于弹性阶段，试件趋于破坏。

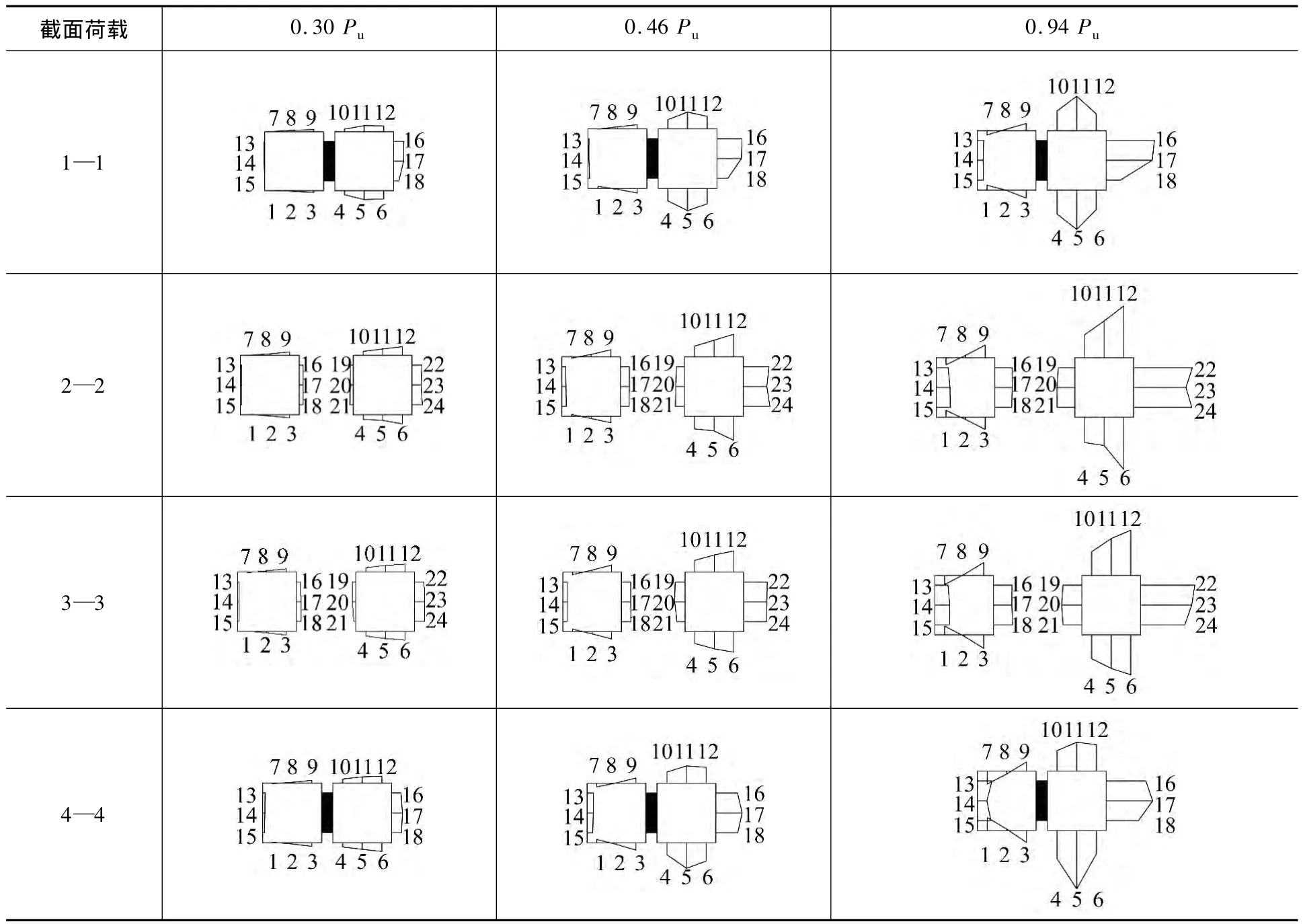
表3 偏心受压时不同荷载作用下各截面正应变分布情况Table 3 Normal strain distributions under eccentric compression testing

4 试验与理论计算对比

将试验值与《钢规》、《薄壁钢规》、《美国国家标准钢结构规范》(ANSI/AISC 360—10)(以下简称《美标钢规》)的计算值进行对比，本试验中拼合钢柱类似于钢结构规范中填板连接的实腹式构件。PS－1表示《钢规》中按格构式构件考虑的计算值;PS－2表示《钢规》中按实腹式构件考虑的计算值;PS－3表示《薄壁钢规》计算值;PS－4表示《美标钢规》计算值;屈服强度取平板的屈服强度340MPa;P0表示试验值;Pu表示全截面达到屈服强度时的承载力。柱子计算长度取“柱长+端板=3 080 mm”，弹性模量按照冷弯转角面积与平板面积加权平均值计算，计算时冷弯转角半径取15 mm，算得转角总面积为384 mm2，平板总面积1 800 mm2，计算公式如下:

对比结果如表4、表5所示。

表4 轴心受压试验与理论计算对比Table 4 The comparison between axial test and theoretical calculations

从表4可看出，全截面达到屈服强度时的承载力较试验值大20%，说明试件未能发生全截面的强度破坏，而发生了失稳破坏。从不同截面形式的《钢规》计算结果与试验值对比来看，拼合钢柱的轴心受压试验值更靠近按填板连接的实腹式构件计算的理论承载力，不同截面的计算值与试验结果相差分别为3．18%和4．65%，且各规范计算值均偏于不安全;与考虑冷弯效应的《薄壁钢规》计算值对比，试验值与规范计算值相差较大，且偏于不安全;与《美标钢规》计算值对比，二者相差不大，美国规范偏安全。

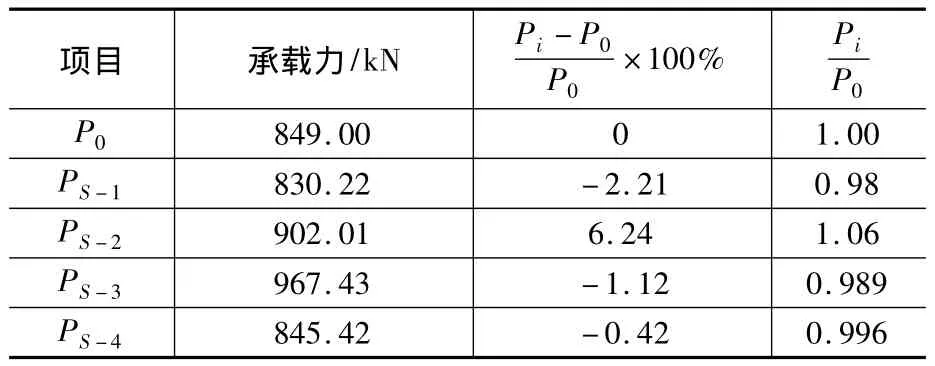
表5 偏心受压试验与理论计算对比Table 5 The comparison between eccentric test and theoretical calculations

从表5可看出，对比不同规范计算结果与试验值，拼合钢柱偏心受压试验值介于格构式截面计算极限承载力与实腹式截面计算极限承载力之间，尽管拼合钢柱的结构特点更接近填板连接的实腹式构件，但拼合钢柱的偏心受压试验值更接近按格构式截面计算的理论承载力，计算值与试验结果均相差不大;与考虑冷弯效应的《薄壁钢规》计算值对比，试验值与规范计算值相差较大，且偏于不安全;与《美标钢规》计算值对比，二者相差不大，美国规范偏安全。

5 结论

冷弯方管拼合钢柱轴压及偏压试验，得到的主要结论如下:

(1)拼合钢柱轴心受压及偏心受压破坏模式均为先单肢局部失稳，继而出现整体失稳。因此，拼合钢柱的极限承载力由稳定条件控制。

(2)轴压试件承载力高于偏压试件，前者为后者的1．55倍;轴压试件的竖向极限变形比偏压试件小，前者为后者的0．53倍;轴压试件的柱中截面极限变形比偏压试件小，前者为后者的0．482倍;耗能能力前者为后者的0．921倍。由此可见，随着偏心距增大，竖向承载力降低，变形能力增加。

(3)本文设计的连接件能有效抗剪，使截面整体共同工作。在连接件部位，钢柱会出现刚度突变。

(4)拼合钢柱轴心受压极限承载力试验值接近实腹式截面的理论极限承载力;偏心受压极限承载力试验值接近格构式截面的理论极限承载力。

［1］ 武胜，张素梅．冷弯新型箱形组合截面受压构件性能研究［J］．哈尔滨工业大学学报，2008，40(2):196-202．Wu Sheng，Zhang Sumei．Behaviors of two new kinds of cold-formed box composite section members under axial compression［J］．Journal of Harbin Institute of Technology，2008，40(2):196-202．(in Chinese)

［2］ 刘向斌，周天华．冷弯薄壁型钢开口三肢拼合立柱轴压性能有限元分析［J］．建筑科学与工程学报，2011，28(3):119-126．Liu Xiangbin，Zhou Tianhua．Finite element analysis of cold-formed thin-walled steel three open limbs built-up columns under axial compression［J］．Journal of Architecture and Civil Engineering，2011，28(3):119-126．(in Chinese)

［3］ 聂少锋，周天华．冷弯薄壁型钢四肢拼合立柱轴压承载力设计方法［J］．土木建筑与环境工程，2011，33(4):20-28．Nie Shaofeng，Zhou Tianhua．Axial bearing capacity design method of cold-formed steel quadruple-c builtup section members［J］．Journal of Cioil，Architecture and Environmcntal Engineering，2011，33(4):20-28．(in Chinese)

［4］ 聂少锋，周天华．冷弯薄壁型钢拼合箱形截面立柱轴压性能试验研究［J］．土木建筑与环境工程，2012，34(4):46-52．Nie Shaofeng，Zhou Tianhua．Experimental analysis on behavior of cold-formed steel box built-up section columns under axial compression［J］．Journal of Civil，Architecture and EnvironmentalEngineering．2012，34(4):46-52．(in Chinese)

［5］ 赵一婕，杜兆宇．冷弯薄壁型钢四肢组合受弯构件承载力研究［J］．湖南大学学报，2012，39(11):28-34．Zhao Yijie，Du Zhaoyu．Analysis of the bearing capacity of cold-formed steel quadruple limbs built-up members under flexural loading［J］．Journal of Hunan University(Natural Science)，2012，39(11):28-34．(in Chinese)

［6］ 周绪红，李拮．冷弯薄壁型钢拼合截面柱轴压承载力计算［J］．建筑科学与工程学报，2012，29(4):1-6．Zhou Xuhong，Li Jie．Calculation method for bearing capacity of cold-formed steel built-up columns under axial compression［J］．Journal of Architecture and Civil Engineering，2012，29(4):1-6．(in Chinese)