基于物理随机地震动模型的汶川地震参数统计与检验

李宗财 刘 威

(1．同济大学建筑工程系，上海200092;2．同济大学土木工程防灾国家重点试验室，上海200092)

1 引言

实测地震时程具有较强的随机性。为了描述地震动的随机性并研究其对结构响应的影响，一般将地震动过程抽象为随机过程［1］，并通常采用功率谱模型描述地震动的随机特性。但功率谱模型仅反映了地震动随机过程的二阶统计特征，无法描述随机地震动的高阶数值统计特征，也无法描述地震动的非平稳特性。

为了克服经典随机地震动模型的局限性，艾晓秋和李杰［2］在2009年建立了考虑工程场地物理机制的随机地震动Fourier幅值谱模型。安自辉和李杰［3－4］通过对 Fourier幅值谱和累计相位谱进行建模，给出了比较完整的地震动物理随机函数模型，并对模型中的随机参数进行了统计。2011年，王鼎和李杰［5－6］基于地震动产生的“震源－传播途径－局部场地”的物理机制，提出了具有物理背景的工程地震动物理随机函数模型，发展了用于合成地震动时程样本的波群叠加方法，并根据场地类型对大量实测地震动时程进行了参数识别。基于上述背景，本文采用文献［5］中模型，对汶川地震进行了参数统计，给出了针对于汶川地震的随机参数的统计特征值。进而，采用等分布序列选点方法［7］获得了地震动时程样本集合并计算了样本集合的反应谱。通过比较样本集合的反应谱和实测地震动记录反应谱的统计特征量，对随机地震动物理函数模型进行了验证。

2 地震动物理随机函数模型

基于地震动产生的“震源－传播途径－局部场地”物理机制，文献［5］提出了工程地震动物理随机函数模型，其表达式为

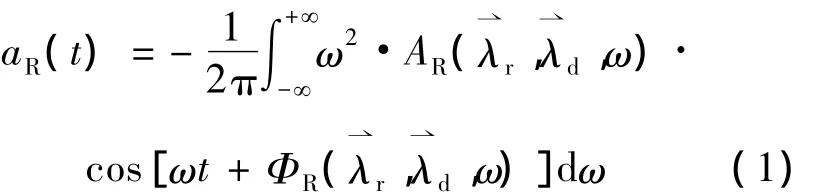
式中，aR(t)为地震动加速度时程;t为时间;ω为圆频率为震中距为R处的地震动Fourier幅值谱和Fourier相位谱模型，其形式由震源、传播途径和局部场地的具体物理模型决定。

震源模型采用Brune位错震源模型，考虑传播途径的阻尼衰减效应和频散效应，并将局部场地等效为单自由度体系;可以得到［5］:

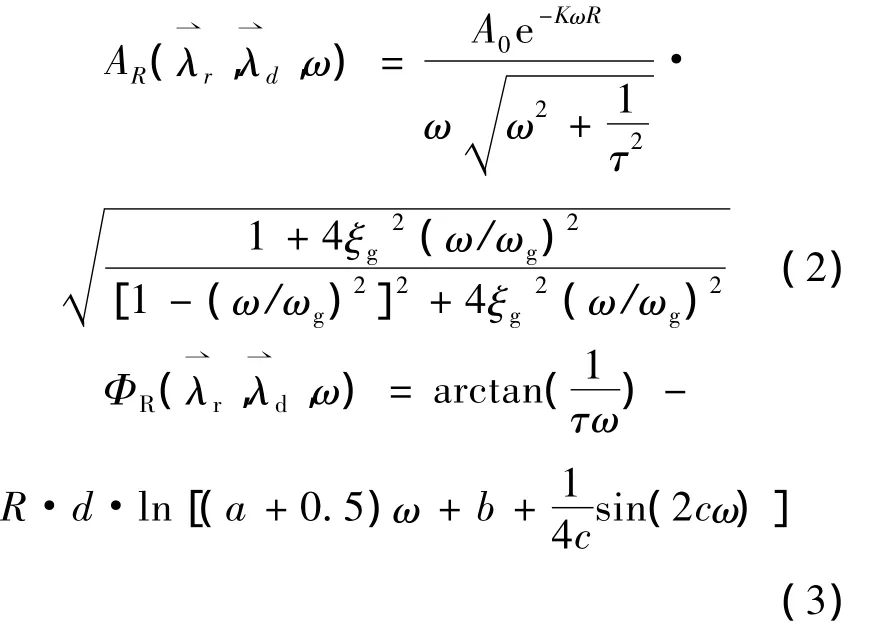
3 汶川地震随机参数识别和统计

选取2008年汶川地震(Ms=8．0)中震中距(R)小于468 km范围东西方向(EW)和南北方向(NS)各137条地震记录进行参数识别和统计。通过调查，在此区域内的场地基本为Ⅱ类场地。地震动时程记录时间间隔为0．02 s，Fourier幅值谱频率范围为0～25 Hz，对于每一条地震记录，采用Fourier变换得到Fourier幅值谱，采用均方逼近准则进行参数识别，即对每一条地震记录可以得到一组参数样本值，使J2达到极小值。

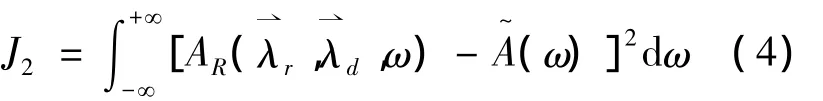
表1 Fourier幅值谱参数拟合结果Table 1 Fitting results of Fourier amplitude spectrum

根据王鼎［6］的参数分布类型，假设幅值系数A0和震源系数τ满足对数正态分布

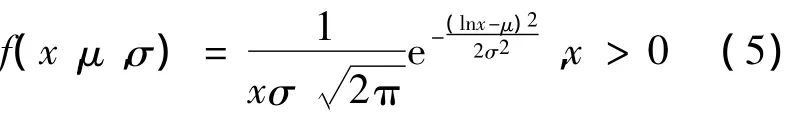
式中，μ和σ为变量对数的均值和标准差。

同样，根据王鼎［6］的参数分布类型，假设场地等效阻尼比ξg和卓越圆频率ωg满足伽马分布:

式中，k为形状参数;1/θ为尺度参数。

采用最大似然估计方法，可以得到各个随机参数的概率分布函数的参数估计结果，采用k－s检验对分布类型进行检验，α为k－s检验的显著性水平，表2给出了各个随机参数的概率分布函数的参数值以及假设分布函数通过k－s检验时的α值。结果表明，本文的假设分布类型具有较高可信度。图3和图4分别给出EW方向和NS随机参数的统计分布图。

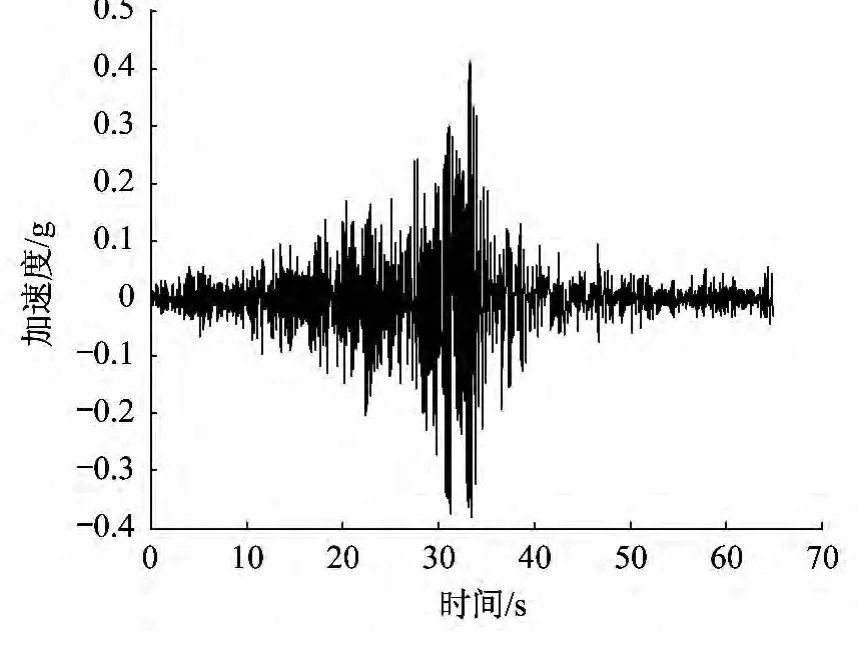
图1 原始加速度时程记录Fig．1 Original ground motion record

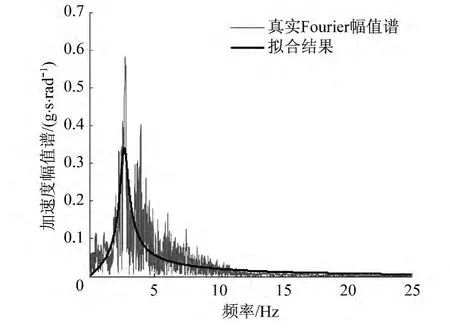
图2 Fourier幅值谱拟合结果Fig．2 Fitting results of Fourier amplitude spectrum

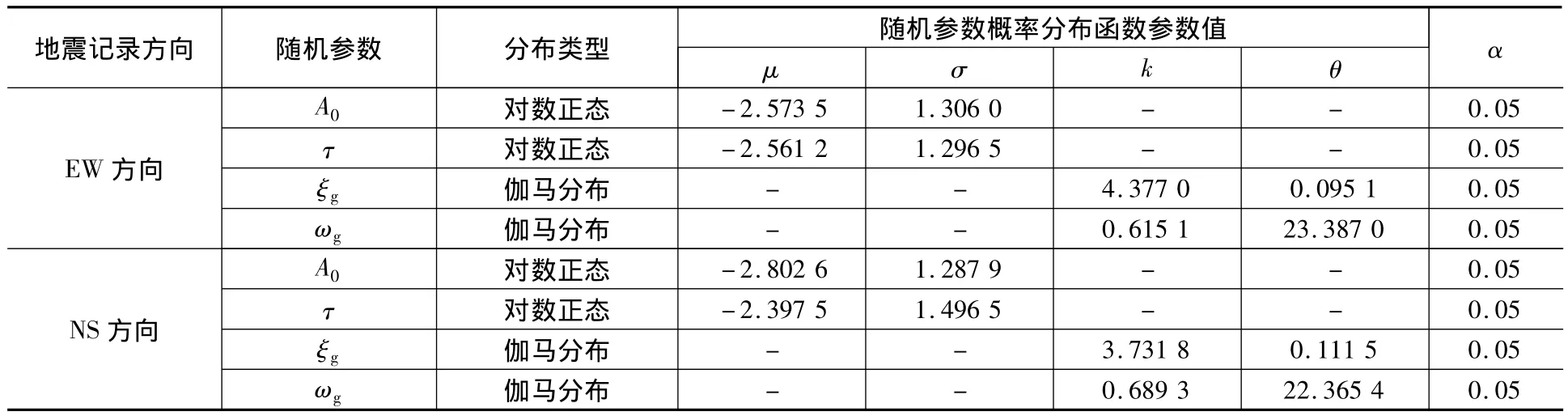
表2 随机参数概率分布函数及参数值Table 2 Probability distribution function of random parameters

图3 EW方向幅值谱参数概率分布Fig．3 Probability distribution of amplitude spectrum parameters in EW direction

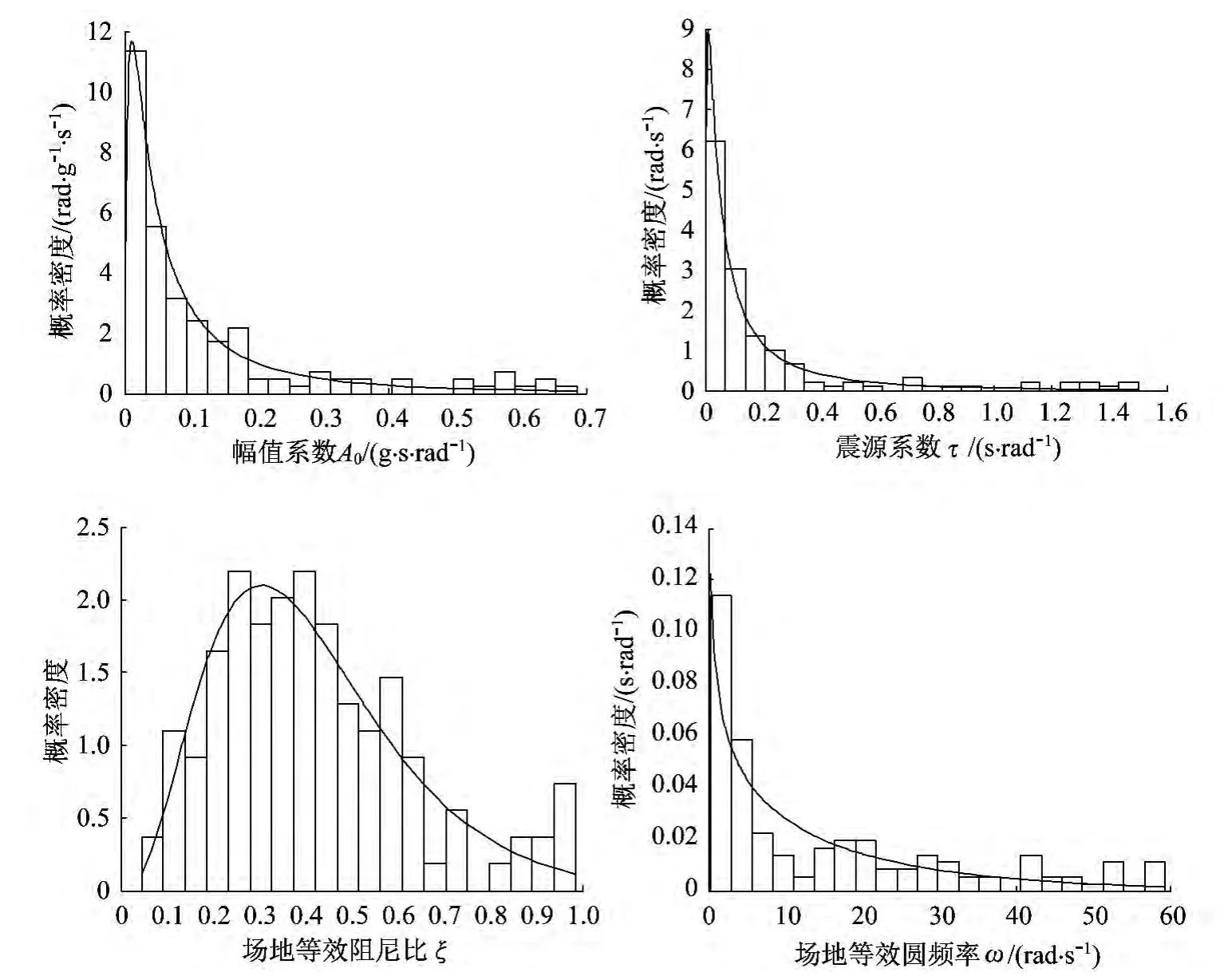
图4 NS方向幅值谱参数概率分布Fig．4 Probability distribution of amplitude spectrum parameters in NS direction

4 物理随机函数模型验证

地震动物理随机函数模型的正确性可以从地震动反应谱的层面上进行验证，假设工程地震动物理随机函数模型中的各个基本随机变量相互独立，则地震动物理随机函数模型的联合概率密度函数可以表示为

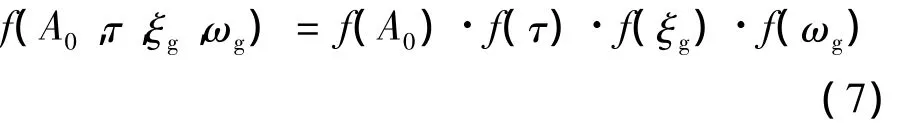
式中，f(A0，τ，ξg，ωg)为模型随机变量的联合概率密度函数;f(A0)，f(τ)，f(ξg)，f(ωg)分别为各随机变量的概率密度函数。

采用等分布序列选点的方法，对基本随机变量的概率空间进行剖分，对EW方向和NS方向随机地震动样本集合，分别选出了119个和116个点代表点，结合波群叠加方法可生成地震动时程样本集合。图5给出了生成的地震动时程样本。

在小阻尼情况下，不难得到地震动加速度时程的反应谱。对于工程地震动物理随机函数模型，可以首先计算各个样本时程的反应谱，结合样本赋得概率可以得到样本集合反应谱的均值和标准差。图6给出了EW方向实测地震记录和生成地震样本集合反应谱的均值和标准差。同时，相应实测地震动记录的反应谱均值和标准差也表示在图6中。从图中可以看出，地震动时程样本集合的反应谱和实测地震记录在均值和标准差上相一致，表明采用物理随机地震动模型可以很好描述地震动特性，得到的统计结果具有比较好的精度。

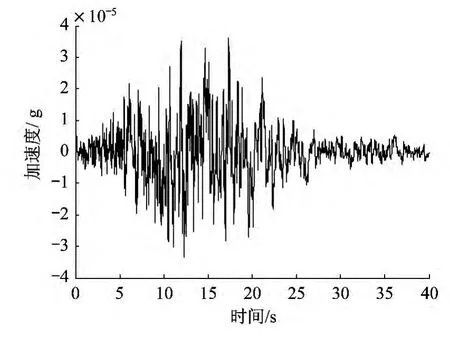
图5 生成的地震动时程样本Fig．5 Generated ground motion sample

5 算例

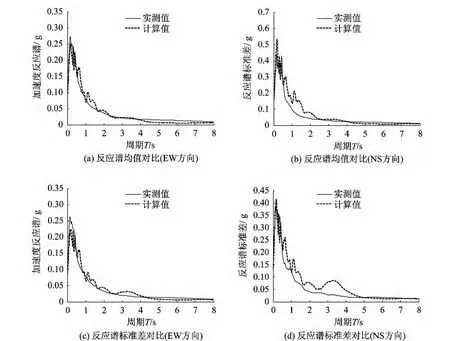
图6 地震动样本和实测地震动记录反应谱均值及标准差比较Fig．6 Comparision of mean and standard deviation of response spectra

由四根长度为250 m的埋地钢管连接成的十字形管网，如图7所示，管材为钢管，弹性模量为2．05 ×105MPa，管径为300 mm，管壁厚15 mm。管线地震反应分析模型采用文献［9］中的模型，单元长度取1．0 m，单位长度管线周围土体弹簧系数为kA=kL=5．65×107N/m2，地震动输入采用行波输入，波速取300 m/s，地震动入射方向与x轴夹角为45°。比较实测地震动作用下管线峰值应力与随机地震动管线峰值应力均值。实测地震动采用汶川地震(2008)中的chnua370089地震记录，震中距148 km，地震动位移时程如图8所示。随机地震动采用等分布序列选点选出128个代表点并通过窄带波群叠加方法生成128条地震动样本。由于模型的对称性，此处给出了AC段管线峰值应力的比较结果，如图9所示，从图中可以看出采用本文生成的随机地震动计算得到的峰值应力均值和实测地震动计算给出的峰值应力基本吻合。

6 结论

(1)根据随机地震动物理随机函数模型，采用汶川地震实测数据，对模型参数进行了拟合。

(2)根据参数拟合结果，统计分析获得了地震动模型基本随机参数的概率密度函数。

(3)利用等分布序列选点方法获得了模型基本随机参量空间的代表点，生成了具有特定赋得概率的地震动时程样本并计算了其反应谱。对比分析表明，地震动时程样本集合的反应谱和实测地震记录的反应谱在均值和标准差上相一致，说明采用物理随机地震动模型可以很好描述地震动特性。

(4)算例分析表明，采用随机地震动计算得到的管线峰值应力均值和实测地震动计算给出的峰值应力基本吻合。

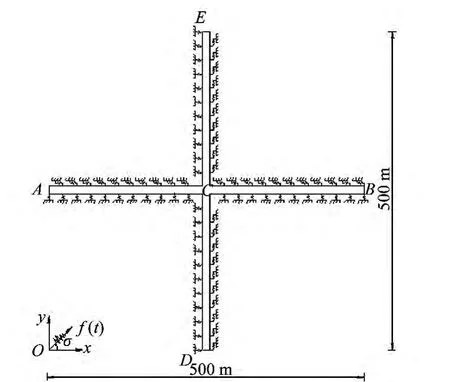
图7 十字形管网Fig．7 Cross pipeline network

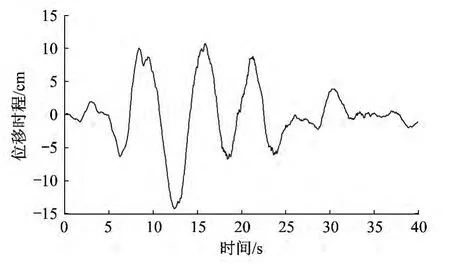
图8 真实地震动位移时程Fig．8 Real displacement record of ground motion

图9 管线峰值应力比较Fig．9 Comparision of the peak stress

［1］ Zerva A，Zervas V．Spatial variation of seismic ground motions:An overview［J］．Applied Mechanics Reviews，2002，55(3):271-297．

［2］ 艾晓秋，李杰．基于随机Fourier谱的地震动合成研究［J］．地震工程与工程振动，2009，29(2):7-12．Ai Xiaoqiu，Li Jie．Synthesis method of non-stationary ground motion based on random Fourier spectra［J］．Journal of Earthquake Engineering and Engineering Vibration，2009，29(2):7-12．(in Chinese)

［3］ 安自辉，李杰．地震动随机函数模型研究 (Ⅰ):模型建立［J］．地震工程与工程振动．2009，29(5):36-45．An Zihui，Li Jie．Research on random function model of strong ground motion(I):model constructing［J］．Journal of Earthquake Engineering and Engineering Vibration，29(5):36-45．(in Chinese)

［4］ 安自辉，李杰．地震动随机函数模型研究(Ⅱ):参数统计与模型验证［J］．地震工程与工程振动．2009，29(6):40-47．An Zihui，Li Jie．Research on random function model of strong ground motion(Ⅱ):parametric statistic and model certification［J］．Journal of Earthquake Engineering and Engineering Vibration，2009，29(6):40-47．(in Chinese)

［5］ 王鼎，李杰．工程地震动的物理随机函数模型［J］．中国科学:技术科学．2011，41(3):356-364．Wang Ding，Li Jie．Physical random function model of ground motions for engineeringpurposes［J］．Science China Technology Scienie．，2011，41(3):356 － 364．(in Chinese)

［6］ 李杰，王鼎．工程随机地震动物理模型的参数统计与检验［J］．地震工程与工程振动，2013，33(4):81-88．Li Jie，Wang Ding．Parametric statistic and certification of physical stochastic model of seismic ground motion for engineering purposes［J］．Journal of Earthquake Engineering and Engineering Vibration，2013，33(4):81-88．(in Chinese)

［7］ Sobol I M．Uniformly distributed sequences with an additional uniform property［J］．USSR Computational Mathematics and Mathematical Physics．1976，16(5):236-242．

［8］ Wong H L，Trifunac M D．Generation of artificial strong motion accelerograms［J］．Earthquake Engineering and Structural Dynamics，1979，7(6):509-527．

［9］ 孙千伟，刘威，李杰．地下管网地震反应分析模型［J］．防灾减灾工程学报，2011，31(6):654-658．Sun Qianwei，Liu Wei，Li Jie．Analysis model of buried pipeline network under earthquake ground motions［J］．Journal of Disaster Prevention and Mitigation Engineering，2011，31(6):654-658．(in Chinese)