分离式双箱组合梁斜拉桥收缩徐变效应分析

苏庆田 戴昌源 许园春

(同济大学桥梁工程系，上海200092)

1 概述

现有的斜拉桥主梁截面有钢主梁形式、混凝土主梁形式和组合梁形式［1］，由于不同材料的强度和密度比值的不同，钢主梁应用于超大跨径斜拉桥而混凝土主梁应用于跨径较小的斜拉桥，组合梁斜拉桥应用于以上两种跨径之间。目前国内外建成的组合梁斜拉桥中大多采用了钢梁格体系与混凝土桥面板组合的形式［2］，东海大桥的主梁采用了槽形钢箱与混凝土组合的形式［3］，近几年一些新型组合梁斜拉桥也开始兴建［4］。

混凝土收缩徐变特有的效应对混凝土结构的影响长期受到关注，已有相对成熟的方法计算分析收缩徐变对混凝土梁桥的影响。近些年随着组合结构桥梁的发展，混凝土收缩徐变效应对组合梁受力性能的影响引起了广泛的关注［5］。在斜拉桥中斜拉索水平分力为组合梁桥面板提供了压应力储备，该较高的应力将导致混凝土徐变的增加［6］。在辅助墩负弯矩区域，收缩徐变可能促使混凝土裂缝提前出现或加速裂缝的扩展，从而导致梁体刚度降低、板中钢筋甚至板下钢梁锈蚀，以至降低结构的受力性能和耐久性，并给养护工作造成很大的困难。因此，有必要计算和分析组合梁斜拉桥的长期受力性能。

本文结合浙江省台州市椒江二桥具体工程，对其采用的分离式半封闭双箱组合梁这一新型组合截面形式进行混凝土收缩徐变效应的影响进行分析。

2 工程简介

椒江二桥主桥是一座主跨480 m的双塔双索面组合梁斜拉桥桥梁，桥跨布置为(70+140+480+140+70)m，总体布置如图1所示。

图1 总体布置图(单位:mm)Fig．1 General layout(Unit:mm)

主梁横断面布置采用分离式双槽形钢梁与混凝土桥面板组成的半封闭组合梁，如图2所示，这是一种新型的组合梁截面形式，是国内首座采用分离式组合梁结构形式的斜拉桥。混凝土桥面板在标准段的厚度为260 mm，在边跨压重段的厚度为400 mm。

分离式半封闭双箱组合梁作为一种新型的组合梁截面形式，其受力特性与传统的组合梁有许多不同之处。这种桥型的收缩徐变尚未有相应的分析，有必要进行相关的研究。

图2 主梁横断面布置图(单位:mm)Fig．2 Composite girder cross section(Unit:mm)

3 计算方法

3．1 计算理论

通常采用徐变系数φ(t，τ)来描述混凝土的徐变。按照欧洲模式规范CEB－FIPMC90［7］和英国标准BS5400［8］第四部分的规定，徐变系数是根据混凝土在28 d时的瞬时弹性模量定义，即时刻τ作用常应力σ(τ)至时刻t混凝土产生的徐变应变。

式中，E28是在28 d时的瞬时弹性模量，εc(t)为徐变应变。

Bazant等［9］对按龄期调整有效弹性模量法进行了严密论证，推导出老化系数的具体计算公式，得到徐变应变εc(t)的表达式如下:

式中，χ(t，τ)为老化系数，可以根据所采用的徐变系数曲线计算得到。

如果采用Dischinger法的表达式，则老化系数可以表示为

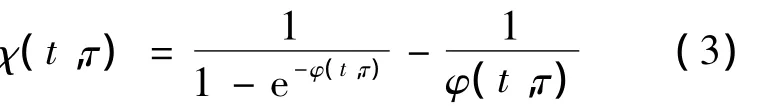
Eφ为按龄期调整的有效弹性模量，计算方法为

对于收缩，一般情况下，普遍认为混凝土的收缩应变与应力历史无关，混凝土的收缩应变可以根据试验结果或者各国规范给出的收缩预测模型直接计算得到。我国的《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD 62—2004)［10］计算混凝土收缩应变公式如下:

式中，ts为收缩开始时的混凝土龄期，可假定为3～7d;t为计算考虑时刻的混凝土龄期(d);εcs0为名义收缩系数;βs(t－ts)为混凝土收缩应变随时间的发展函数。

混凝土的名义收缩系数εcs0主要受混凝土强度及构件所处环境的年平均相对湿度影响，其计算式为

式中，fcm为混凝土在28d龄期时的平均立方体抗压强度(MPa);收缩开始时的混凝土龄期，可假定为3～7 d;βRH为混凝土收缩应变随时间的发展函数。规范给出了公式中的 εcs，βRH和 βs(t－ts)的计算方法。

3．2 有限元分析模型和基本参数

本文选用有限元分析软件ANSYS建模全桥的空间有限元模型。模型中使用三主梁模型模拟组合梁中的混凝土桥面板和两个钢箱梁，混凝土桥面板和钢梁均采用beam44单元，主梁之间用刚臂连接;混凝土桥塔采用beam44单元模拟，斜拉索采用link8单元模拟，空间有限元模型如图3所示。

钢梁为 Q345钢材，弹性模量为2．1×105MPa，密度为7 850 kg/m3;桥面板板为C60混凝土，弹性模量为 3．6×104MPa，密度为 2 600 kg/m3，斜拉索弹性模量为 1．9 × 105MPa，密度为7 850 kg/m3。

图3 有限元模型Fig．3 FEM model

3．3 荷载效应

计算过程中，荷载只考虑结构自重效应。从成桥状态开始考虑收缩徐变的影响。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD 62—2004)［10］规定的方法计算了混凝土的徐变系数和收缩量，按龄期调整有效弹性模量法计算徐变，将混凝土桥面板的弹性模量进行修改计算，将收缩按照换算等效的温度作用。在有限元模型计算的每个荷载步里面，分别修改相应的混凝土弹性模量和降温作用，得到成桥之后不同时间的受力情况。

4 计算结果分析

由于该桥纵桥向跨径布置为对称结构，本文只给出了半幅桥的计算结果。取纵桥向跨中中点为内力图和应力图中横坐标零点，桥塔位于距离跨中240 m的位置，辅助墩位于距离跨中380 m的位置。

4．1 成桥时桥梁受力情况

首先分析了斜拉桥在自重荷载作用下受力情况，这里给出了组合梁中混凝土部分和钢梁部分的受力情况分别如图4和图5所示。

从图4可以看到，组合梁桥面板混凝土的轴向力全部为负值，说明全部的桥面板混凝土受到轴向压力作用，压力在跨中和边跨端部位置较小，向靠近索塔逐渐增加，最大轴向力为125 846 kN;桥面板的弯矩分布特点是:以辅助墩处为界，向中跨方向一侧弯矩比较小，向另一侧的弯矩稍大，且有一定的波动，这主要是在辅助墩到边跨端部的这一段梁体存在压重作用的结果。在轴向力和弯矩作用下桥面板混凝土的上、下缘以压应力作用为主，压应力总体规律是从跨中和边跨端部向桥塔处逐渐增大，局部由于受到斜拉索索力的作用使得上、下缘的应力出现一定范围的波动，同时，在辅助墩处，应力出现一个局部的增大。在辅助墩一侧，存在拉应力作用。拉应力最大值为1．4 MPa。桥面板混凝土的应力最大值出现在桥塔附近，上、下缘的最大压应力分别为15．6 MPa和20．6 MPa。

图4 混凝土受力情况Fig．4 Concrete mechanical behavior

图5 钢梁受力情况图Fig．5 Steel girder mechanical behavior

从图5可以看到分离式双箱组合梁中的一个钢箱的轴力分布在纵桥向较为复杂，其中在靠近中跨跨中部位轴力为正、在靠近桥塔部位的轴力为负、在辅助墩附近的轴向压力有一定的变化;钢梁的弯矩在纵桥向总体较小，在辅助墩、靠近桥塔左右的第一对拉索处有一定的波动。钢梁上缘的应力在中跨跨中和边跨端部附近较小而在靠近桥塔处较大，最大压应力为66．8 MPa，钢梁下缘的应力在中跨跨中处表现为拉应力，最大为52．5 MPa，其它部位总体呈现压应力，最大压应力为80．6 MPa。

4．2 徐变作用下桥梁受力情况的变化

在徐变作用下，钢梁的轴力、弯矩和应力变化情况如图6所示。图中给出了从成桥开始到成桥后3年、5年和10年时段的考虑徐变作用的主梁受力情况。

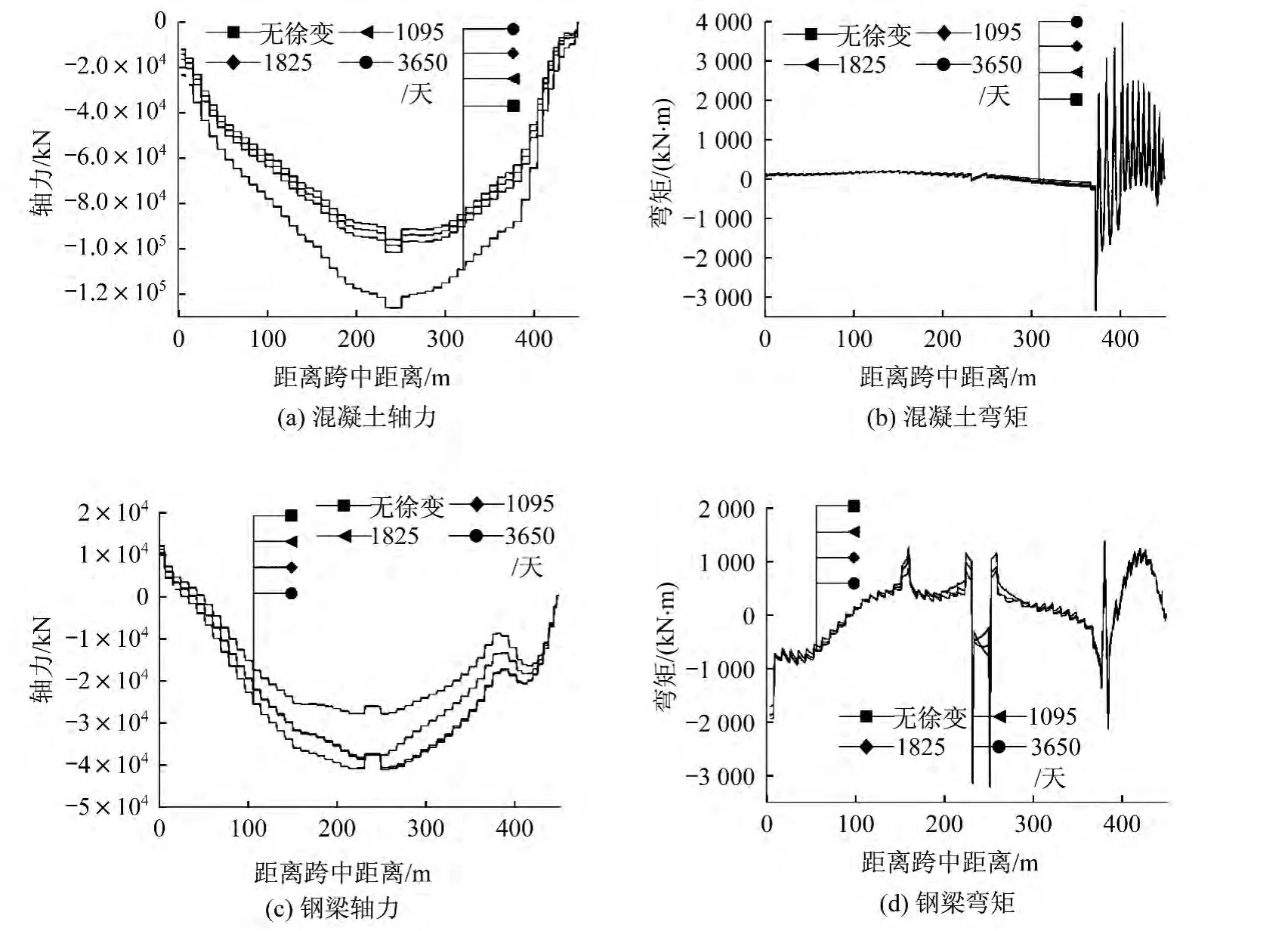
图6 混凝土徐变效应的影响Fig．6 Effect of concrete creep

从图6可以看出:混凝土徐变对组合梁混凝土和钢结构的轴力和弯矩影响程度不同，其中对弯矩影响较小，对轴力影响较大。主要原因是在斜拉桥中主梁总体上受到轴向压力作用为主，弯矩作用较小，徐变效应也表现出相应不同的影响程度。从图6(a)中看出由于徐变效应使得混凝土的轴力随时间的增加而减少，特别是在前3年的变化量远大于后期的变化。同样从图6(c)中看出由于徐变效应使得钢梁的轴力随时间的增加而增大，前3年的增加量非常明显，在第5年到第10年的变化量基本相同。总体而言对于斜拉桥组合梁由于徐变效应使得混凝土和钢结构的轴向力发生重分配，混凝土的轴力减少而钢结构的轴力增加。

表1和表2给出了斜拉桥主梁不同位置截面处混凝土和钢梁由于徐变效应引起的具体应力数值。表中位置数值表示距离主跨跨中截面的距离，下文同。

表1 徐变引起的混凝土应力变化Table 1 Concrete stress variation from creep

表2 徐变引起钢梁应力变化Table 2 Steel stress variation from creep

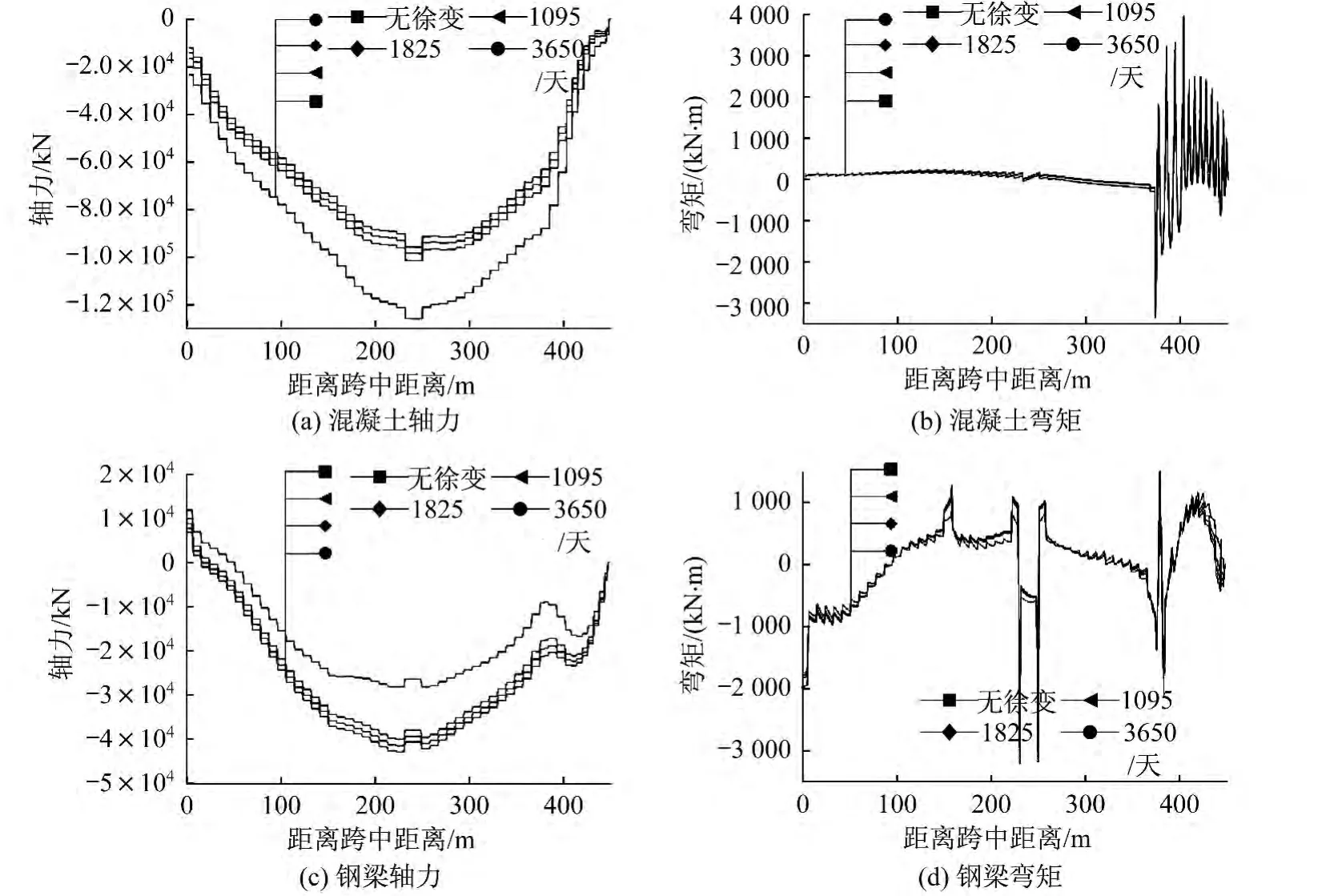
图7 收缩效应的影响Fig．7 Effect of concrete shrinkage

从表1和表2中可以看出:总体上由于徐变效应导致组合梁中钢梁承担的轴力在增大、混凝土承担的轴力在减少。在相同的时间下不同截面处混凝土和钢梁的应力变化率各不相同，在相同时间同一截面钢梁应力增加率和混凝土应力减小率也不相同。一方面是钢梁和混凝土在不同位置处受到轴力和弯矩的具体效应不同，导致总体的应力在不同位置相差较大;另一方面，混凝土的厚度、钢梁板件厚度在桥梁纵桥向也不同，造成不同截面处钢梁的刚度与混凝土的刚度不同，从而在内力重新分配的关系比例上也不同。另外从表1和表2中得出靠近桥塔附近主梁的应力最大，在3年时由于徐变效应引起该部位的混凝土压应力减少7%、钢梁压应力增加32%，在10年时由于徐变效应引起该部位的混凝土压应力减少10%、钢梁压应力增加34%。

4．3 收缩作用下桥梁受力情况的变化

考虑收缩作用时，钢梁的轴力、弯矩和应力变化情况如图7所示。

从图7可看出，由于混凝土收缩效应，组合梁上混凝土和钢梁的内力发生一定的变化。其变化规律与徐变效应的相似，组合梁混凝土的轴向压力随时间的增加逐渐减少，钢梁的轴向压力随时间的增加逐渐增大。主要是由于混凝土的收缩变形受到钢梁的约束，导致钢梁的压力增大、混凝土产生一定的拉力。混凝土和钢梁的内力前3年的变化量远大于后5年的。由于收缩效应引起组合梁中混凝土和钢梁的弯矩变化不明显。

表3和表4给出了斜拉桥主梁不同位置截面处

混凝土和钢梁由于收缩效应引起的具体应力数值。

表3 收缩效应下混凝土应力变化Table 3 Concrete stress variation from shrinkage MPa

表4 收缩作用下钢梁关键部位应力变化表Table 4 Steel stress variation from shrinkage

从表3和表4中可以看出:和徐变类似，在收缩作用下，组合梁在相同时段不同截面上钢梁和混凝土的应力变化率各不相同，同一截面相同时段的钢梁和混凝土应力变化也不相同。靠近桥塔附近主梁的应力最大，在3年时由于收缩效应引起该部位的混凝土压应力减少11%、钢梁压应力增加37%，在10年时由于收缩效应引起该部位的混凝土压应力减少14%、钢梁压应力增加45%，在辅助墩附近混凝土拉应力在逐渐增大，达到了1．6 MPa。钢梁的内力、应力均发生了较大的变化。

5 结语

分离式双箱组合梁与常规组合梁相似，在收缩和徐变作用下内力发生了重分布。但是由于斜拉桥主梁的高次超静定以及分离式组合梁截面的变化，收缩和徐变效应对组合梁内力重分配与常规组合梁有较大不同，在分离式双箱组合梁不同位置截面上的混凝土和钢梁应力变化比例相差较大。

［1］ 林元培．斜拉桥［M］．北京:人民交通出版社，2004．Lin Yuanpei．Cable-stayed Bridge［M］．Beijing:China Communication Press，2004．(in Chinese)

［2］ 高宗余，张强，王应良．组合结构主梁斜拉桥设计进展［J］．铁道勘察，2007，(S1):50-53，100．Gao Zongyu，Zhang Qiang，Wang Yingliang．Evolution of design on hybrid beam cable-stayed bridge with combined structure［J］．Railway Investigation and Survey，2007，(S1):50-53，100．(in Chinese)

［3］ 邵长宇．钢—混凝土箱形结合梁斜拉桥在东海大桥的应用与展望［J］．桥梁建设，2003，(3):5-8．Shao Changyu．Application and prospective of cablestayed spans of steel-concrete composite box girder for East China Sea Bridge［J］．Bridge Construction，2003，(3):5-8．(in Chinese)

［4］ 曾明根，徐嘉煜，赵佳男，等．椒江二桥组合梁施工过程中剪力钉局部受力分析与设计优化［J］．结构工程师，2011，27(5):62-67．Zeng Minggen，Xu Jiayu，Zhao Jianan，et al．Mechanical analysis and design optimization for stud connectors of composite girders in Second Jiaojiang Bridge uring construction［J］．Structural Engineers，2011，27(5):62-67．(in Chinese)

［5］ 樊健生，聂建国，王浩．考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅰ)-试验及计算［J］．土木工程学报，2009，42(3):8-15．Fan Jiansheng，Nie Jianguo，Wang Hao．Long-term behavior of composite beams with creep，shrinkage and cracking(Ⅰ):experiment and calculation［J］．China Civil Engineering Journal，2009，42(3):8-15．(in Chinese)

［6］ 吴冲，曾明根，邵长宇，等．大跨度组合箱梁斜拉桥混凝土收缩与徐变应力分析用与展望［J］．世界桥梁，2004，(增 1):37-41．Wu Chong，Zeng Minggen，Shao Changyu，et al．Analysis of concrete shrinkage and creep stresses of longspan composite box girder cable-stayed bridges［J］．World Bridges，2004，(S1):37-41．(in Chinese)

［7］ 欧洲国际混凝土委员会．CEB-FIPMC90欧洲混凝土结构模式规范［S］．北京:中国建筑科学研究院，1991．CES．CEB-FIPMC90 Model Code for Concrete Structures［S］．Beijing:China Academy of Building Research，1991．(in Chinese)

［8］ 英国标准学会．钢桥混凝土桥及结合梁桥(英国标准BS5400)［S］．成都:西南交通大学出版社，1986．British Standard Institution．Steel，concrete and combined girder bridges(BS5400)［S］．Chengdu:Southwest Jiaotong University Press，1986．(in Chinese)

［9］ Bazant Z P．Prediction of concrete creep effects using age-adjusted effective modulus method［J］．ACI Journal，1972，69(2):212-217．

［10］ 中华人民共和国交通部．JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京:人民交通出版社，2004．Ministry of Transport of the People's Republic of China．JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］．Beijing:People Communications Press，2004．(in Chinese)