误差不相关广义线性模型极大拟似然估计的收敛速度

尹长明, 刘双花, 陈波红

(1.广西大学 数学与信息科学学院, 南宁 530004; 2.百色学院 数学与统计学院， 广西 百色 533000；3.广西民族大学 相思湖学院， 南宁 530008)



误差不相关广义线性模型极大拟似然估计的收敛速度

尹长明1*, 刘双花1,2, 陈波红1,3

(1.广西大学 数学与信息科学学院, 南宁 530004; 2.百色学院 数学与统计学院， 广西 百色 533000；3.广西民族大学 相思湖学院， 南宁 530008)

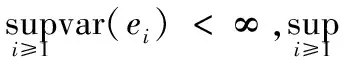
广义线性模型; 拟似然估计; 弱收敛速度

1 引言和主要结果

广义线性模型(GLM)是对经典线性模型的重要推广,它既适用于连续数据, 又适用于离散数据,特别是后者.自从Nelder 和Wedderburm[1]引入此模型以来,它已被应用到许多领域.尤其在生物和医学数据的统计分析上有重要意义.

设响应变量yi是相互独立的,协变量Zi是已知的p×1向量,yi服从指数分布

exp(θiyi-b(θi))dv(yi),i=1,…,n.

(1)

假设yi的期望与线性预测因子Zi′β有下列关系

Eyi=h(Zi′β),

(2)

其中,h是充分光滑的单调函数,β∈Rp是未知的回归参数,β0是它的真值.函数h的逆称为联系函数.对数似然方程

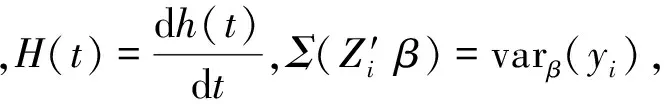
在许多情形下假定yi服从指数分布(1)是不切实际的,而且Σ(·)的确切表达式不知道.但若关于期望的假定(2)是正确的,仍可用Wedderburn[2]引入的拟似然方法,用拟似然方程

(3)

的根估计β0,称它为极大拟似然估计(MQLE),其中,Λ(·)>0是适当选择的方差函数.详细情况可参看文献[3].

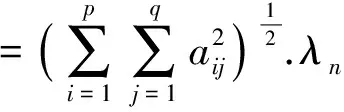
关于GLM的MLE或MQLE的渐近理论,文献中有不少讨论,可参见文献[4-10].文献[4-7]和文献[8-9]分别研究了ei,i=1,2,…是独立和鞅差情形MLE或MQLE的渐近性质;文献[10]研究了ei,i=1,2,…不相关,自然联系函数MQLE的弱收敛速度;本文用不同的方法得到了ei,i=1,2,…不相关,一般联系函数MQLE的弱收敛速度,即下面的定理1.

定理1若下列假定(A1)～(A3)成立.

(A3)H(t)≠0,Λ(t)>0且Λ(t)导函数连续,

(4)

且

(5)

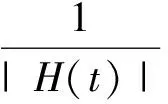
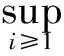
2 定理的证明

由中值定理知

ln(β)-ln(β0)=-Qn(β*)(β-β0),

(6)

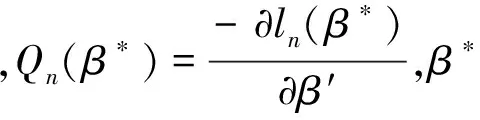
先证当n→∞时,

(7)

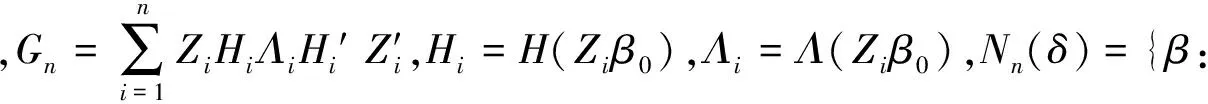
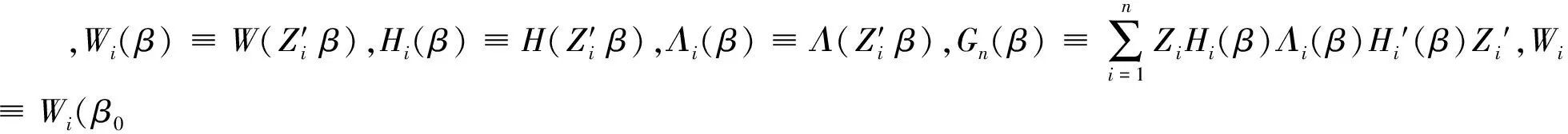
(8)

其中,

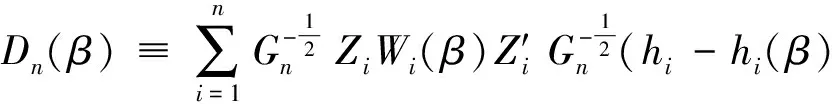
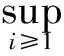
(9)

由假定(A3)知Γ(t)∶=H(t)Λ(t)H′(t)在紧集上一致连续,再由(9)式知

(10)

用λs记第s个元素为1,其余元素为0的p×1向量.下面证当n→∞时,

(11)

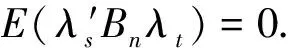
与证明(9)式同理,由假定(A1)和(A3)知,

所以(11)式成立.

所以,当n→∞时,

(12)

同理,当n→∞时,

(13)

由(8)、(10)、(11)、(12)和(13)式,知(7)成立.

下面证对任意ε>0,存在δ>0,当n充分大时,

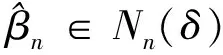
(14)

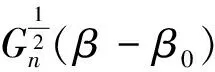
由Cauchy-Schwarz不等式知对任意δ>0,

Qn(β*)(β-β0)≥

(15)

由(7)式,知对任意ε>0,δ>0,当n充分大时,

(16)

由(6)、(15)和(16)式,知对任意δ>0,当n充分大时,

(17)

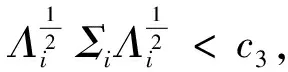
(18)

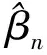
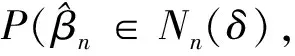
(19)

即(4)式成立.

[1]NelderJA,WedderburmRWM.Generalizedlinearmodels[J].JRoyStatistSocSerA, 1972, 135:370-384.

[2]WedderburnRWM.Quasi-likelihoodfunctions,generalizedlinearmodels,andtheGauss-Newtonmethod[J].Biometrika, 1974, 61:439-447.

[3]FahrmeirL,TutzG.MultivariateStatistcalModellingBasedonGeneralizedLinearModels[M].NewYork:Springer-Verlag, 1994.

[4]FahrmeirL,KanfmannH.Consistencyandasymptoticnormalityofthemaximumlikelihoodestimatoringeneralizedlinearmodels[J].AnnStatist, 1985, 13:342-368.

[5]LiYue,ChenXiru.Ratesofa.s.convergenceofthemaximumquasi-likelihoodestimatoringeneralizedlinearmodels[J].ScienceinChina,SerA(inChinese), 2004, 34:203-214.

[6]YinCH,ZhaoLC,WeiCD.Asympoticnormalityandstrongconsistencyofmaximumquasi-likelihoodestimatesingeneralizedlinearmodels[J].ScienceinChinaSerA, 2006, 48:145-157.

[7]YinCM,LiYM,WangPY.Strongconvergenceratesofthemaximumquasi-likelihoodestimatoringeneralizedlinearmodels[J].ActaMathematicaScientiaSerA, 2009, 29:1058-1064.

[8]ChenK,HuI,YingZ.Strongconsistencyofmaximumquasi-likelihoodestimationingeneralizedlinearmodelswithfixedandadaptivedesigns[J].AnnStatist, 1999, 27:1155-1163.

[9]GaoQB,LinJG,ZhuCH,etal.Asymptoticpropertiesofmaximumquasi-likelihoodestimatorsingeneralizedlinearmodelswithadaptivedesigns[J].Statistics, 2012, 46:833-846.

[10]ZhangSG,LiaoY.Onsomeproblemsofweakconsistencyofquasi-likelihoodestimatesingeneralizedlinearmodels[J].SciChinaSerA, 2008, 51:1287-1296.

Rate of weak consistency of maximum quasi-likelihood estimator in generalized linear models

YIN Changming1, LIU Shuanghua1,2, CHEN Bohong1,3

(1.School of Mathematics and Information Science, Guangxi University, Nanning 530004； 2.School of Mathematics and Statistics, Baise University, Baise, Guangxi 533000；3.Xiangsihu College, Guangxi University for Nationalities, Nanning 530008)

generalized linear models; quasi-likelihood estimator; rate of weak consistency

2014-12-02.

国家自然科学基金项目(11061002，11361007);广西自然科学基金项目(2011gxnsfa018126)； 百色学院一般科研项目(2014KB09)；广西高校数学及其应用重点实验室项目.

1000-1190(2015)05-0665-03

O212.1; O212.4

A

*E-mail: yinchm@gxu.edu.cn.