基于计算全息的强鲁棒性自适应水印算法

白韬韬，刘 真，卢 鹏

（上海理工大学 出版印刷与艺术设计学院，上海200093）

1 引 言

计算机技术和网络通信的飞速发展，使得数字产品的获取、使用、传播变得异常便捷。随着版权保护问题的日益突出，数字音频、视频、图像的版权保护也引起了越来越多的重视，成为当今社会和广大学者的研究热点。数字水印技术［1－5］为解决版权保护问题提供了一个有效的途径，已经广泛应用到了版权保护领域。目前，大多数水印算法都是针对数字图像的传播、保护进行设计，且只能有效抵抗一些常见的图像处理攻击，对印刷稿图像的版权无法进行有效的保护。但是印刷图像的版权保护同等重要，如何设计一种算法使得数字图像即可以有效抵抗打印扫描攻击，又可以有效抵抗一般图像处理攻击是该领域的难点问题。

近年来，结合现代信息光学技术的数字全息水印日益受到学者关注。2002年，Takai等［6］首次将数字全息技术引入数字水印领域，提出了数字全息水印技术。虽然该方法结合了全息图像良好的抵抗裁切攻击的性能，但是由于其选择在空间域将原始图像和全息水印直接叠加，并且水印嵌入前要对原始图像做低通滤波处理，细节信息大量丢失，导致含水印图像视觉质量差，且安全性不高，抵抗其他攻击的能力也有待进一步提高。随后，许多学者［7－10］对全息水印及其嵌入方式进行了 大 量、深 入 的 研 究。2007 年，Sun 等［11－12］提出了加密同轴全息水印技术，该种技术可以抵抗图像的打印扫描攻击，并取得了初步的成果。但其得到的含水印图像视觉效果较差。并且由于同轴全息解密生成共轭像，使得从全息图恢复出的图像背景叠加了严重的噪声，对水印图像的辨别产生影响。2008年，Sun等［13］提出了彩色印刷图像的计算全息数字水印。但是其并没有说明算法抵抗其他图像处理攻击的鲁棒性。2009 年，Huang等［14］提出了一种新的生成计算全息的方式，即共轭对称延拓傅立叶计算全息，并在2011年将生成的全息水印嵌入到图像中［15］，实现了含水印图像经打印扫描后的水印提取。但是水印的安全性和抵抗其他图像处理攻击的能力需要进一步提高。

本文提出了一种基于计算全息的强鲁棒性自适应水印算法，充分利用了Contourlet变换在图像处理中的独特优点——多方向性和各向异性来自适应隐藏两个水印信息，设计水印算法。实验证明，本算法具有较高的安全性和不可见性，可以抵抗一般的图像处理攻击，并且经过打印扫描后提取出的水印信息清晰。

2 基于计算全息的强鲁棒性自适应水印算法

2.1 共轭对称延拓傅立叶计算全息

本文利用共轭对称延拓傅立叶计算全息方法生成全息水印图像。设原始实值水印图像为已经归一化的f（x，y），图像的大小为mpixel×npixel.待记录的复数图像φ（x，y）＝f（x，y）exp［j2πp（x，y）］，其中p（x，y）为［0，1］范围内均匀分布的随机数。

将复数图像φ（x，y）进行共轭对称延拓，得到M pixel×N pixel大小的复数图像，其中M＝2×（m＋1），N＝n＋1。如式（1）：

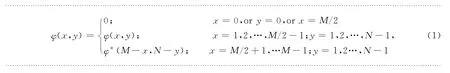
式中：上标“＊”表示对复数做共轭运算，Φ（x，y）为共轭对称延拓后的复数图像。对Φ（x，y）做二维离散傅立叶变换，得到实值的全息图像.设得到的全息图像为H（x，y），则：

式中：F 表示傅立叶变换。由傅立叶变换的性质，即共轭对称的复数矩阵经过快速傅立叶变换得到实值矩阵，Φ（x，y）经过DFT 后得到实值图像H（x，y）。此实数图像记录了复值图像Φ（x，y）的振幅和相位信息。将此图像经过适当编码即可得到实值数字全息图。

2.2 Contourlet变换

2002年，Do和Vetterli［16］提出了一种“真正”的图像二维表示法：Contourlet变换。Contourlet变换，也称金字塔型方向滤波器组PDFB（Pyramidal Directional Filter Bank）。PDFB 首先利用拉普拉斯金字塔（Laplacian Pyramid，LP）变换对原始图像进行多尺度分解，以“捕获”二维图像信号中存在的奇异点。然后由方向滤波器组（Directional Filter Bank，DFB）将分布在同方向上的奇异点连成线，形成轮廓段。PDFB 通过双滤波器组将多尺度分析和方向分析分开进行，这种互补的结构使其具有较优的非线性逼近性能。Contourlet变换不仅继承了小波变换的多分辨率和时频局部性，而且允许每个尺度上有不同数目的方向，提供了更高水平的方向性和各向异性。图1和图2分别给出了Contourlet对图像进行分解的过程示意图和Contourlet变换频域子带分布示意图。图3 展示了应用Contourlet变换对lena图像进行二级分解的结果，高频和中频分别分解为4方向和8方向。

图1 Contourlet变换分解Fig.1 Contourlet transform decomposition

图2 Contourlet变换尺度和方向分布Fig.2 Frequency subbands distribution of Contourlet transform

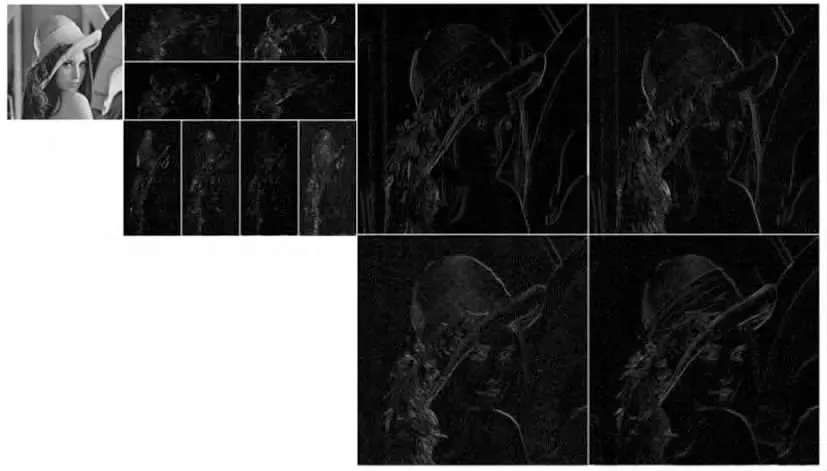
图3 灰度图像lena的Contourlet分解结果Fig.3 Contourlet decomposition results of the gray image“lena”

2.3 算法分析

由于全息图像本身信息量大，一般二值水印嵌入方法无法嵌入大信息量的全息水印，使得利用全息图像作为水印的算法较少，并且多数全息水印算法无法有效抵抗JPEG 压缩等常见的图像处理攻击。为了增强算法的鲁棒性，本文嵌入了两个全息水印图像，进一步增加了水印的嵌入量，所以本文选择具有很高冗余性的Contourlet变换域嵌入水印信息。Contourlet变换冗余度为4／3，这种性质非常适合隐藏大信息量的全息水印。目前，基于Contourlet变换的数字水印算法［17－20］也提出了很多，但现有大多数算法都是简单利用LP分解出的低频信息更加稳定这一特点来设计水印算法，并没有充分利用Contourlet变换在图像处理中特有的优势：更高水平的方向性和各向异性这一特点，并且应用此种变换结合全息技术设计的数字水印算法并不多见。本文正是考虑到Contourlet变换可以将LP分解出的中高频信息进行多方向分解，提供更多水印嵌入位置这一特性来隐藏水印。在嵌入位置选择上，本文进行了巧妙的设计，由于分解出的各个中频子带信息与全息图像的相似度不同，故当全息水印替换不同中频信息完成水印嵌入后，逆变换得到的含水印图像与原始图像的PSNR 值也会产生很大的变化。所以本文将得到的PSNR 最大值对应的图像作为最终的含水印图像，可以在不损失相似度的情况下进一步提高嵌入强度，实现了水印的自适应嵌入，增强算法的鲁棒性。本文算法充分利用了Contourlet变换多方向性和各向异性的特点，将全息水印以本文设计方法自适应嵌入到原始图像稳定的中频信息中，使其可以有效抵抗JPEG 压缩、低通滤波攻击等一般图像处理攻击和打印扫描攻击。

3 水印的嵌入与提取

3.1 全息水印的预处理

利用2.1节共轭对称延拓计算全息生成两个初始全息水印图像，大小均为M pixel×N pixel。针对生成的全息图像安全性差的问题，本文采用一种简单、有效的双水印预处理加密方法。首先，利用随机分散矩阵将两幅全息图像随机分散合成一个图像。然后，将图像分割成两个大小为M pixel×N pixel的图像，作为加密后的待嵌入全息水印。具体步骤如下：

（1）利用共轭对称延拓计算全息生成两个大小为M pixel×N pixel的全息水印图像。

（2）随机生成一个大小为M×2 N，只包含0，1的矩阵作为随机分散矩阵，其中0，1 数量各占一半。

（3）当随机分散矩阵中某一位置的值为0时，在合成图像对应位置记录第一个全息图像的像素值，反之，记录第二个全息图像的像素值，依次类推。即两个全息图像被随机分散到一个合成图像中。

（4）将合成全息图像分割成两个大小为M pixel×N pixel的图像，即为加密后的待嵌入全息水印。

（5）记录随机分散矩阵，作为解密密钥。

3.2 全息水印的嵌入

首先，将原始图像进行二级Contourlet变换，将中频信息进行8方向分解，得到8个中频子带图像。其次，将两个加密后的待嵌入全息水印自适应的替换原始图像的中频子带，实现水印的嵌入。最后，做二级Contourlet逆变换，得到含水印图像。具体步骤如下：

（1）将4 M pixel×8 N pixel大小原始图像进行二级Contourlet变换，两级分解分别为4方向和8方向，得到8个大小为M pixel×N pixel（或N pixel×M pixel）的中频子带图像。

（2）将双全息水印自适应的替换原始图像中频信息，以实现水印信息的嵌入。为缩小所替换中频信息的范围，分别计算待嵌入水印与8个中频子带的PSNR 值，并记录由大到小前3 个PSNR 值对应的中频系数编号。

（3）将水印信息按所得编号随机替换两个中频子带图像，实现水印的嵌入。具体公式如下：

式中：LLi为原始图像的中频子带图像，i为步骤2 中记录的编号。watermarkj为全息水印，j＝1，2。当j不同时，i的编号也有可能相同。k为嵌入系数。

（4）做二级Contourlet逆变换，得到含水印图像。计算其与原始图像的PSNR，并记录全息水印替换的中频子带编号。

（5）重复步骤3～4，得到PSNR 值最大时对应的中频子带编号。对应的含水印图像即为自适应嵌入水印得到的含水印图像。

（6）记录所替换中频子带的编号，作为提取水印的密钥。

3.3 全息水印的提取

水印提取过程为水印嵌入过程的逆过程，本文的水印检测无需原始图像，为盲水印。具体步骤如下：

（1）将待检测图像进行二级Contourlet变换，两级分解分别为4方向和8方向，得到8个大小为M pixel×N pixel（或N pixel×M pixel）的中频子带。

（2）根据存储的中频子带的编号提取出水印信息并合并。

（3）利用存储的随机分散矩阵，恢复出两个原始全息水印图像。

（4）对恢复的全息图像做逆傅立叶变换得到水印信息。

4 仿真实验

为了验证本算法的有效性，实验采用1 024 pixel×1 024pixel大小的8bit灰度lena图像作为实验的原始图像，如图4（a）所示。原始水印图像采用127pixel×127pixel大小的二值图像，如图4（b）和4（c）所示。利用共轭对称延拓计算全息生成两幅全息水印，用3.1节的预处理方式，将两幅全息水印加密，得到如图5（a）和5（b）所示的加密图像。利用正确的分散矩阵对加密全息图像解密，并做逆傅立叶变换得到原始水印，如图5（c）和5（d）所示。

图4 原始图像和水印图像Fig.4 Original image and watermark images

图5 加密全息图及其再现Fig.5 Encryption and reconstruction of holograms

本文用峰值信噪比（PSNR）来客观评价两幅图像的相似程度。利用3.2节的方法将双水印嵌入到原始图像中。水印嵌入系数k 取为0.4，由3.2节步骤2计算两个水印分别与8个方向子带的PSNR 值，如表1所示。得到由大到小前3个PSNR 值对应的中频系数编号均为4、6、8。将双水印对应替换不同的中频系数（所要替换中频系数编号均为4、6、8），不同替换组合得到的含水印图像与原始图像PSNR 值如表2所示。

由表2知，当两个全息水印的嵌入强度确定时，替换不同中频系数，得到的PSNR 值从37.402 5变化到38.385 7，变化范围较大。需要说明的是，如果替换与水印图像相似度更小的中频子带，PSNR 值的变化范围更大。本文正是利用Contourlet变换提供的更高水平的多方向性设计隐藏水印，使得在嵌入强度确定的情况下，找到最优的嵌入位置，使得PSNR 提高。达到了在不牺牲相似度的前提下，提高水印嵌入强度的目的，嵌入强度的提高使其抵抗攻击能力也进一步增强。

本文实验中，两个水印所替换的中频系数其编号分别为6 和8，含水印图像和原始图像的PSNR 值为38.385 7，客观说明了两幅图像的相似度很高。图6所示为含水印图像和用正确的密钥提取出的水印图像。从图中可以看出提取的水印信息清晰。本文仿真实验中，提取出的水印图像均未做任何处理。为了说明本算法除了可以抵抗打印扫描攻击外，还具有更好的抵抗一般图像处理攻击的鲁棒性，本算法将与文献［15］算法进行对比实验。需要说明的是，文献［15］算法是将一个水印信息嵌入在原始图像中，且得到的含水印图像与原始图像的PSNR 值为37.5dB，小于本算法的PSNR。为保证嵌入的水印图像相同，对比实验中采用的水印图像为双水印的拼接图像。为了对比实验直观，从文献［15］提取的水印再裁切成两个水印进行效果对比。

表1 两个全息图与8个方向子带的PSNR 值Tab.1 PSNR between two holograms and eight directional subbands

表2 原始图像与替换不同方向子带所得水印图像的PSNR 值Tab.2 PSNR between original image and watermarked images

图6 含水印图像和提取的水印图像Fig.6 Watermarked image and extracted watermark images

4.1 双水印预处理安全性测试

由于选用的全息图生成方式几乎没有安全性，故采取一种简单的双水印预处理方法提高其安全性。加密后的全息图像如图5（a）和（b）所示，用错误的随机分散矩阵恢复的图像，经过逆傅立叶变换得到的图像如图7所示，均为无意义的图像。

由实验可知，本文使用的双水印预处理方法简单、安全性好。因为两幅原始全息图的信息被随机分散，只占每个加密全息图的一部分；加密图像所含的信息是两幅原始全息图的部分信息随机组合，这样会对全息图的逆傅立叶变换解密产生相互干扰。所以，即使正确提取出嵌入的水印信息，如果没有密钥矩阵，也无法恢复出原始的双水印信息。

图7 错误的随机分散矩阵恢复的图像Fig.7 Reconstruction images using wrong random scatter matrix

4.2 JPEG 压缩攻击实验

JPEG 图像压缩是最常见的图像处理攻击之一，所以能否有效抵抗JPEG 压缩攻击也是评价一个算法鲁棒性的重要指标。如图8所示，标号a～f和m～r的图像是本算法提取出来的水印图像。对应的压缩质量因子分别为20、30、40、50、60、80。标号g～l和s～x图像为文献［15］算法提取的水印图像。

图8 JPEG 压缩攻击实验Fig.8 Experiment for attack of JPEG compression

由图8 可以看出，文献［15］算法在抵抗JPEG 压缩攻击方面存在很大缺陷，只有当压缩因子为50及以上时，提取的水印信息才有一定的主观辨识性，但是也没有本算法提取的水印清晰。由于Contourlet域的中低频具有很强的稳定性，故本算法可以有效抵抗JPEG 压缩攻击，当压缩因子在30 及以上时，提取出的水印信息均很清晰，视觉辨识度很高，当压缩因子为20时，提取的水印信息也有一定的视觉辨识度。说明本算法抵抗JPEG 压缩攻击的鲁棒性强。

4.3 噪声、低通滤波攻击

水印算法对噪声攻击和对滤波攻击的鲁棒性也是评价算法优劣的重要指标。为了检验本文提出算法对噪声攻击和滤波攻击的鲁棒性强弱，本文选用的噪声攻击有加性噪声：高斯噪声和椒盐噪声，也有乘性噪声：speckle噪声；低通滤波攻击有高斯滤波，中值滤波和均值滤波。选用的噪声攻击其均值都为0，高斯噪声的方差为0.002，椒盐噪声的方差为0.01，speckle噪声的方差为0.03；高斯滤波选用7×7大小模版，中值滤波和均值滤波均选用3×3大小模版。如图9所示，标号a～f和m～r的图像是本算法从受到上述攻击的对应含水印图像中提取出来的水印图像。标号g～l和s～x图像为文献［15］算法对应提取的水印图像。

图9 噪声和滤波攻击实验Fig.9 Experiment for attack of noise and low－pass filtering

由图9可知，本文算法和文献［15］算法对加性噪声攻击都有很好的抵抗能力，但本算法抵抗spckle乘性噪声的能力更强，提取的水印更加清晰；本文算法抵抗滤波攻击的能力强于文献［15］算法，提取的水印背景噪声较少。这是因为文献［15］算法，将水印隐藏在图像小波变换的对角线中频系数中，当受到滤波攻击时，小波中频信息的稳定较差而受到破坏，导致提取的水印背景有很明显的、不均匀的对角线噪声。实验说明本算法可以有效抵抗噪声和低通滤波攻击，提取的水印信息均清晰、辨识度高。

4.4 裁切攻击

由于全息图的不可撕毁性，该算法对裁切攻击也有很强的抵抗能力。本文将含水印图像分别进行裁切10%和30%处理。如图10所示，编号（a）和（b）为从裁切10%的含水印图像中提取出的水印信息，编号（c）和（d）为从裁切30%的含水印图像中提取出的水印信息。由图可以看出，提取出的水印信息清晰，本算法可以有效抵抗裁切攻击。

图10 剪切攻击实验Fig.10 Experiment for attack of cropping

4.5 打印扫描攻击

打印扫描实验中采用的打印机型号为HPZ3200彩色打印机，打印分辨率为150dpi；采用的扫描仪型号为EPSON V500，扫描分辨率为600dpi。本算法生成的图像经打印扫描后得到电子图像，从中提取出的水印信息如图11（a）和图11（b）所示。从图中可以看出，本算法得到的水印信息清晰，视觉辨识度高，说明本算法除了有很强的抵抗一般图像处理攻击的鲁棒性外，还可以有效抵抗打印扫描攻击。

图11 打印扫描攻击实验Fig.11 Experiment for print－scan attack

图12 打印扫描和JPEG 压缩混合攻击实验Fig.12 Experiment for hybrid attack of print－scan and JPEG compression

JPEG压缩是最常见的图像处理攻击，图像很可能经过压缩后用于打印输出，所以算法对JPEG压缩和打印扫描混合攻击的鲁棒性也是一个重要的指标。图12（a）和图12（b）所示为本算法得到的含水印图像，经过压缩因子为30的JPEG 压缩攻击和打印扫描攻击后提取出的水印信息。文献［15］生成图像经过相同操作得到的水印如图12（c）和图12（d）所示。从图中可以看出，文献［15］算法提取出的水印信息已经无法辨认，说明该算法无法有效抵抗JPEG 压缩和打印扫描混合攻击，而本文提出的算法提取出的水印信息依然清晰可辨，说明本算法可以有效抵抗这种常见的组合攻击，鲁棒性很强。

5 结 论

基于CGH 和Contourlet变换提出了一种基于计算全息的强鲁棒性自适应水印算法。利用Contourlet变换冗余信息量大有利于水印隐藏、在图像处理中的独特优势——多方向性和各向异性，以及其中、低频信息更加稳定这些特点，将双全息水印自适应的隐藏到图像Contourlet变换的中频部分，使得在PSNR 值保持相对较高的情况下，水印嵌入的强度增强，提高了算法抵抗攻击的能力。实验结果表明：利用本算法得到的含两个全息水印的图像与原始图像的PSNR 值达到了38.385 7，说明本算法有很强的不可见性。本算法不仅可以从打印扫描攻击后的图像中提取出清新可辨认的水印信息，也对JPEG 压缩攻击的鲁棒性强，压缩因子达到30时，提取的水印依然可以清晰辨认。同时对剪切、噪声和低通滤波攻击均有很强的抵抗能力。并且本算法可以抵抗常见的JPEG 压缩和打印扫描的混合攻击，提取出的水印信息清晰可辨认。在水印提取时，不需要借助原始图像，属于盲水印算法。本文所提出的数字水印算法不仅可以保护数字图像，也可以对印刷图像进行有效的版权保护。

［1］ 李新娥，班皓，任建岳，等.一种多传感器图像融合与数字水印技术［J］.液晶与显示，2014，29（2）：286－292.Li X E，Ban H，Ren J Y，et al.Method of multisensory image fusion and digital watermarking［J］.Chinese Journal of Liquid Crystals and Displays，2014，29（2）：286－292.（in Chinese）

［2］ 申静.一种利用人眼视觉特性的数字图像水印技术［J］.液晶与显示，2011，26（2）：234－240.Shen J.Digital image watermarking technology based on human vision characteristics［J］.Chinese Journal of Liquid Crystals and Displays，2011，26（2）：234－240.（in Chinese）

［3］ Papakostas G A，Tsougenis E D，Koulouriotis D E.Moment－based local image watermarking via genetic optimization［J］.Applied Mathematics and Computation，2014，227：222－236.

［4］ Ishtiaq M，Jaffar M A，Choi T S.Optimal sub－band and strength selection for blind watermarking in wavelet domain［J］.Imaging Science Journal，2014，62（3）：171－177.

［5］ Chen C H，Tang Y L，Wang C P，et al.A robust watermarking algorithm based on salient image features［J］.Optik，2014，125（3）：1134－1140.

［6］ Takai N，Mifune Y.Digital watermarking by a holographic technique［J］.Applied Optics，2002，41（5）：865－873.

［7］ 马建设，任振波，苏萍，等.多重计算全息水印技术［J］.光学精密工程，2013，21（8）：2111－2120.Ma J S，Ren Z B，Su P，et al.Multiple watermarking technique based on computer－generated hologram［J］.Optics and Precision Engineering，2013，21（8）：2111－2120.（in Chinese）

［8］ Martinez C，Laulagnet F，Lemonnier O.Gray tone image watermarking with complementary computer generated holography［J］.Optics Express，2013，21（13）：15438－15451.

［9］ Li J Z.Robust image watermarking scheme against geometric attacks using a computer－generated hologram ［J］.Applied Optics，2010，49（32）：6302－6312.

［10］ Giuseppe S S，Michele D S.Holographic watermarking for authentication of cut images［J］.Optics and Lasers in Engineering，2011，49（12）：1447－1455.

［11］ 孙刘杰，庄松林.双随机相位加密同轴傅里叶全息水印防伪技术［J］.光学学报，2007，27（4）：621－624.Sun L J，Zhuang S L.Forgery prevention based on inline fourier holographic watermark with double random phase encrypt ion［J］.Acta Optica Sinica，2007，27（4）：621－624.（in Chinese）

［12］ 孙刘杰，庄松林.加密同轴全息数字水印［J］.光学精密工程，2007，15（1）：131－137.Sun L J，Zhuang S L.Digital watermarking of encrypted in－line holography［J］.Optics and Precision Engineering，2007，15（1）：131－137.（in Chinese）

［13］ 孙云峰，翟宏琛，杨晓苹，等.傅立叶计算全息数字水印在彩色图像印刷防伪中的应用［J］.光电子·激光，2008，19（7）：952－955.SunY F，Zhai H C，Yang X P，et al.Application of Fourier CGH digital watermarking technique in color image Forgery－Prevention printing［J］.Journal of Optoelectronics·Laser，2008，19（7）：952－955.（in Chinese）

［14］ 黄素娟，王朔中，于瀛洁.共轭对称延拓傅里叶计算全息［J］.物理学报，2009，58（2）：952－958.Huang S J，Wang S Z，Yu Y J.Computer generated holography based on Fourier transform using conjugate symmetric extension［J］.Acta Physica Sinica，2009，58（2）：952－958.（in Chinese）

［15］ 黄素娟，王杜瑶，刘晓静，等.基于小波变换的硬拷贝全息水印［J］.光电子·激光，2011，22（9）：1415－1420.Huang S J，Wang D Y，Liu X J，et al.Hardcopy hologram watermarking based on discrete wavelet transform［J］.Journal of Optoelectronics·Laser，2011，22（9）：1415－1420.（in Chinese）

［16］ Do M N，Vetterli M.Contourlets：A new directional multiresolution image representation［C］.Signals，Systems and Computers，2002，1：497－501.

［17］ Ranjbar S，Zargari F，Ghanbari M.A highly robust two－stage Contourlet－based digital image watermarking method［J］.Signal Processing：Image Communication，2013，28（10）：1526－1536.

［18］ Qin，C，Wen，X B.A novel digital watermarking algorithm in Contourlet domain［J］.Journal of Information and Computational Science，2014，11（2）：519－526.

［19］ Mo J，Ma Z F，Huang Q L，et al.An adaptive watermarking scheme using SVD in Contourlet domain［J］.Advances in Information Sciences and Service Sciences，2012，4（15）：221－232.

［20］ Jiang A P，Yao D.A Contourlet watermarking algorithm based on fractal dimension and one－dimensional logistic chaotic encryption［J］.International Journal of Advancements in Computing Technology，2012，4（19）：317－323.