基于改进突变级数法的矿山地质灾害危险性评价——以潞安矿区为例

王 洋 马施民 许 珂

基于改进突变级数法的矿山地质灾害危险性评价
——以潞安矿区为例

王 洋 马施民 许 珂

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

为避免矿山地质灾害危险性的传统评价方法对于评价指标权重的计算以及主观赋权所存在的不足，以潞安矿区为例，提出了一种基于熵值法的改进突变级数法并用于对矿山地质灾害危险性进行评价。在系统分析该矿区主要地质灾害类型及特征的基础上，以该矿区5个典型生产矿井为例，首先根据矿山地质灾害类型及特点，构建了矿山地质灾害危险性评价指标体系，其次利用熵值法确定同层评价指标的相对重要程度，然后利用突变级数法中的归一化公式计算出不同矿井的总突变隶属度值，最后运用转化后的等级标准对该矿区地质灾害危险性进行评价。结果表明：该方法不仅避免了人为确定权重的主观性，而且能够定量区分出同一层次指标的重要程度；该方法的评价结果与实地野外调查结果基本一致，可为矿山地质灾害危险性评价和有效防治提供科学依据。

矿山地质灾害 危险性评价 熵值法 突变级数法 地质灾害类型 评价指标体系 突变隶属度

潞安矿区位于山西省东南部，沁水煤田东部中段，行政区划隶属长治市、潞城市及襄垣、长子、壶关、长治、屯留等县。潞安矿区是山西省12个国家煤炭规划矿区之一，煤炭资源丰富，开发条件有利，矿区经过50余a的开采，在有力支援国民经济建设的同时，也引发了十分严重的地质灾害问题，尤其是随着采空区面积的越来越大，煤炭开采引发的地表变形破坏越来越严重。据相关调查统计，五阳、王庄、漳村、常村、夏店等5个典型矿井因煤炭开采形成的塌陷面积达79.19 km2，使得大片良田变成池沼，公路出现变形、沉陷，井泉干涸，民房变形、开裂，给当地的交通、人民生活和经济发展带来了较为严重的影响。

为了更有效地评价矿山地质灾害，学者们采用了诸如模糊综合评判法[1-3]、灰色聚类分析法[4-5]、信息量模型[6-7]、组合赋权法[8-10]等定量评价矿山地质灾害，该类方法基本都是通过确定合理的评价指标体系和每项指标的具体权重，构建各自的数学评价模型来实现，在一定程度上能够反映矿山地质灾害的危险程度，但该类方法中构建的部分评价模型计算过于复杂，且客观确定各项指标的具体权重难度较大。为此，本研究在系统分析潞安矿区地质环境背景和地质灾害发育特征的基础上，提出了一种改进突变级数法的矿山地质灾害危险性评价方法，力求从定量的角度客观评价潞安矿区典型矿井的地质灾害危险性，为矿区内煤炭资源安全开采、地质环境保护、地质灾害有效防治提供依据。

1 潞安矿区地质灾害发育特征

潞安矿区地质灾害主要为煤炭开采形成的地面沉陷、地裂缝以及少量的潜在崩塌，地质灾害规模以中小型为主。潞安矿区地质灾害主要分布于王庄矿、五阳矿、漳村矿等几个典型生产矿井的采空区范围内，主要包括襄垣县南部、长治县北部、屯留县东部和长子县东部等地。该类区域由于开采规模大、开采强度高、采煤历史久等因素，使得该地区的地质灾害普遍发育且分布集中。

(1)沉陷积水区。潞安矿区采煤沉陷区分布较广，加之大气降水或疏降排水的影响，形成诸多或孤立存在、或彼此串珠状联通的沉陷积水区(见图1)。尤其是所属的王庄煤矿为国有现代化生产矿井，开采强度高、采煤历史悠久，沉陷区内有24个明显的积水盆地，累计沉陷总面积达25.13 km2[11-12]。该类积水盆地常年或季节性积水，使得土地完全无法耕种。

图1 沉陷积水区Fig.1 Subsidence water area

(2)波浪状沉陷。是由相邻的条带状“波谷”塌陷区构成的面状区域，单个“波谷”一般长轴长600～1 200 m，短轴长100～200 m，深3～5 m，长轴方向与采煤工作面走向大体一致。该类沉陷大多分布于堆积冲洪积平原区，主要分布于矿区中南部，地势平坦开阔，一般高程500～1 000 m，其浅部主要由第四系冲洪积物组成，岩性以黏土、淤泥质为主(见图2)。

图2 波浪状沉陷Fig.2 Wavy subsidence

(3)采空区边缘拉张裂缝。该类裂缝位于采煤形成的采空区的外边缘，规模较大，裂缝长30～400 m，宽0.1～0.6 m，形态特征多为直线状或环状。裂缝的力学性质为张性，裂缝两侧土体在垂直方向上有明显的位移。该类裂缝影响了土地的平整度与完整性，破坏了原有的地貌形态，降低了土地利用价值，加速了水土流失和土地退化进程。

(4)地堑式裂缝。主要分布于中低山丘陵区，地层以石炭系、二叠系为主，上覆松散层较薄，岩性以砂岩、泥质软硬互层为主。裂缝主要分布于煤柱、采区边界的边缘地带以及地表较陡的土坡边缘地带，主要是一系列平行或弧状落差明显的地表裂缝(见图3)。该类裂缝在丘陵山区危害最大的是可能形成小型崩塌、滑坡等次生灾害。

图3 采空区边缘地堑式裂缝Fig.3 Graben group fissures of gob edge

(5)小型崩塌。潞安矿区的西部丘陵地带由于地面沉陷导致大量节理裂隙发育，裂隙多呈张开型，宽1～5 cm不等，最大可达10 cm以上，该类裂缝破坏了岩体完整性，降低了岩体力学强度。在地势陡峭，存在有效临空面发育的地区易形成小型黄土崩塌(见图4)。

2 地质灾害危险性评价

2.1 突变级数法基本原理

突变级数法是一种基于突变理论和模糊数学理论的综合评价方法，核心是利用突变理论分叉方程所推导出的归一化公式建立一种多指标、多层次综合评价问题的递归运算法则，避免了直接使用难以确定且主观性较大的“权重”概念。由于归一化公式在一定程度上反映了评价指标之间的作用机理，因而该方法能够较为合理、定量地考虑各评价指标的重要性[13]。

图4 小型黄土崩塌Fig.4 Small loess collapse

突变理论的研究对象是势函数，评价过程中需根据势函数对评价目标(状态变量)进行分类，当上一层评价目标包含的下一层指标(控制变量)的个数分别为1，2，3，4个时，分别构成折叠型、尖点型、燕尾型和蝴蝶型等4类突变模型[14-15]，见表1。突变级数法评价的基本步骤：①将矿山地质灾害危险性逐层次分解，建立多指标、多层次评价指标体系，并考虑同层次指标间的相对重要程度；②根据指标体系的层次结构，确定不同的突变模型，将各层次的控制变量按归一化公式进行量化递归运算，采用“大中取小”的非互补性或取平均值的互补性原则，计算各层次的突变模糊隶属度函数；③计算评价对象的总隶属度函数，并建立突变级数判据，从而对评价对象的危险性进行评价。

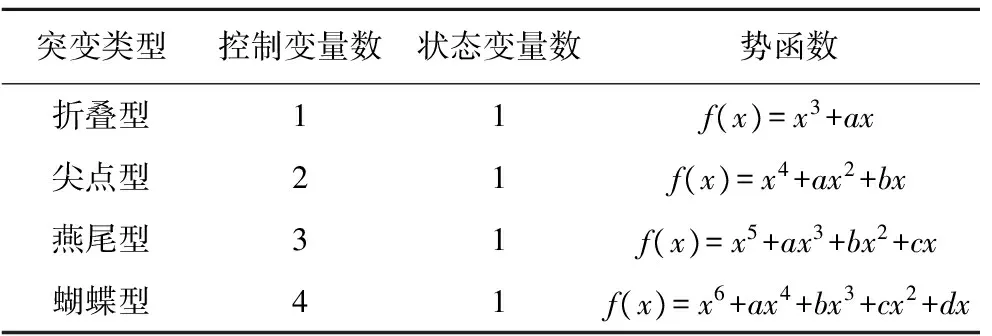
表1 常用突变模型的势函数Table 1 Optimization functions of commonly used catastrophe models

2.2 评价过程及结果

2.2.1 评价指标体系建立

通过分析潞安矿区地质环境背景以及地质灾害发育特征，建立了包含目标层、准则层和指标层的潞安矿区地质灾害危险性评价的指标体系，见图5。

图5 评价指标体系Fig.5 Evaluation index system

2.2.2 控制变量归一化处理

本研究通过专家打分并结合德斐尔法对指标数据进行无量纲化处理[16]，即多位专家参照表3中指标的等级区间标准，按百分制原则对各指标进行赋分量化，再通过德斐尔法对专家的赋分值进行处理，确定其对应的四分位数，最后将此数除以100即可(见表2)。

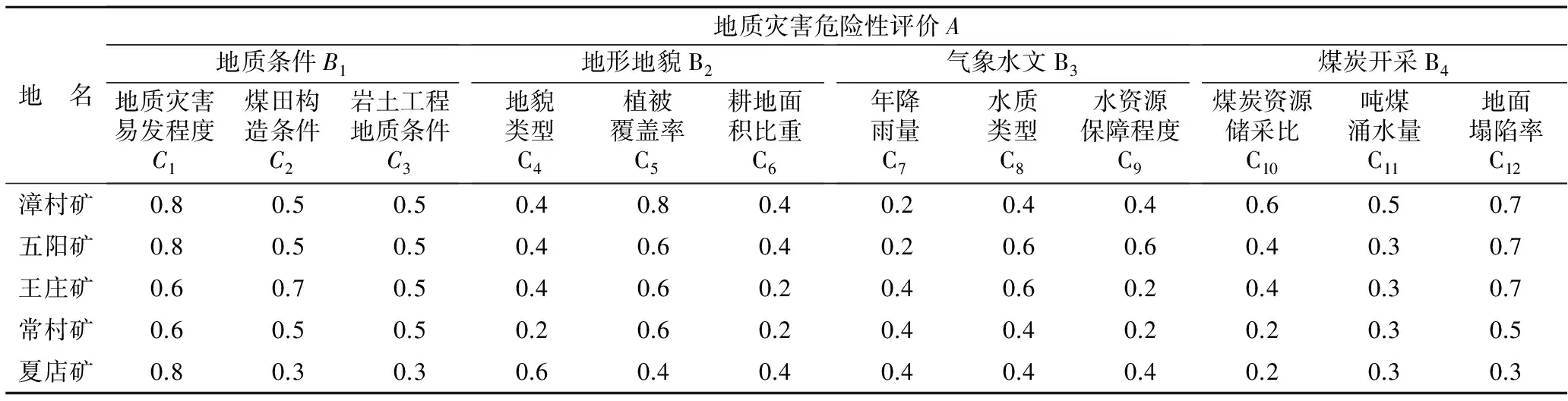
表2 潞安矿区典型矿井地质灾害危险性评价指标分值Table 2 Index values of geological disaster risk evaluation in typical mines of Luan mining area

表3 地质灾害危险性级别隶属度值Table 3 Membership values of the risk levels of geological disasters

根据突变理论，平衡曲面方程可通过计算方程f′ (x)=0得到，平衡曲面的奇点集方程可通过计算方程f′′ (x)=0得到。计算方程f′ (x)=0 和f′′ (x)=0，可得突变系统的分歧点集方程。当各状态变量满足该分歧点集方程时，系统即发生突变。该分歧点集方程无法直接用来评价，需要导出归一化公式，将各状态变量和控制变量的取值限制在0～1范围内。因而推导出表1中4类突变类型的归一化公式分别为折叠型(xa=a1/2)，尖点型(xa=a1/2、xb=b1/3)，燕尾型(xa=a1/2、xb=b1/3、xc=c1/4)，蝴蝶型(xa=a1/2、xb=b1/3、xc=c1/4、xd=d1/5)[17-18]。

2.2.3 基于熵值法改进的评价指标重要性排序

突变级数法在评价时无需计算每项指标的具体权重，但需考虑同层次指标间的相对重要程度，为此，本研究引入熵值法来区分同一层次指标的重要程度。该方法是一种客观赋权方法，通过计算指标的信息熵，根据各指标信息熵值的效用价值决定指标的权重，信息效用值较大的指标具有较大的权重。假定评价指标体系包括m个样本，n个指标，则可形成评价系统的初始数据矩阵

首先对各指标进行无量纲化处理[19]，然后计算第j项指标下第i个样本指标值比重yij，最后计算第j项指标的信息熵值(由于仅需确定指标的相对重要性，故无需继续计算具体权重)，从而得出各指标层的信息熵值为0.994,0.980,0.990,0.967,0.986,0.969,0.969,0.987,0.946,0.946,0.984,0.974。由熵值法可知，熵值越小其权重值越大，即该指标在系统中越重要，因此根据信息熵值得出的各指标层指标的权重排序为C2>C3>C1，C4>C6>C5，C9>C7>C8，C10>C12>C11。以各指标层指标信息熵的均值计算出准则层指标的信息熵值，从而确定出准则层指标的权重排序为B3>B4>B2>B1。

2.2.4 突变模型及评价原则选择

目标层与准则层之间和准则层与指标层之间分别构成蝴蝶型突变系统和燕尾型突变系统。因此，本研究在对矿山地质灾害危险性评价时采用的突变系统有蝴蝶型和燕尾型2类。评价原则的选取需要根据指标之间联系的实际情况，按照互补性或非互补性的原则进行。如果各指标之间无明显联系，则采用“大中取小”(取最小值)的非互补性原则；各指标之间如果存在相互促进或相互抵制的联系，则采用取平均值的互补性原则[20]。根据分析计算，各控制变量间可互相弥补不足，且共同可对状态变量产生作用，因此，采用取平均值的互补性原则进行计算。

2.2.5 评价模型的计算过程

依据上述指标评价原则及指标重要性排序，应用燕尾型和蝴蝶型突变模型的归一化公式，通过突变模糊隶属度函数首先计算控制变量的突变隶属度值，然后逐层向上计算，最终计算其总隶属度值。以王庄矿为例，准则层与指标层之间按燕尾型归一化公式进行计算，首先计算出准则层的突变隶属度值分别为0.666 7，0.516，0.666 7，0.569；目标层与准则层之间按蝴蝶型归一化公式进行计算，从而计算出目标层的总隶属度值为0.853 7。因此，王庄矿地质灾害危险性评价值为0.853 7，依据上述原则及方法，可得潞安矿区5个典型矿井的地质灾害危险性评价结果。

2.2.6 评价指标值转化

突变理论评价体系中，突变级数法得到的综合评价值能够反映各典型矿井之间的危险程度，却无法有效划分地质灾害危险性等级。为克服突变评价法的上述缺陷，将底层指标的隶属度等级阈值转化为最终的总隶属度等级阈值，如此，底层指标的等级标准便转化为最终综合评价值的等级标准，在此基础上将计算出的各典型矿井的综合评价值根据所在的等级范围转化为具有绝对“优”、“劣”含义底层指标的隶属度值，从而获得各典型矿井最终的危险性评价等级，见表4。

表4 潞安矿区典型矿井地质灾害危险性评价结果Table 4 Geological disaster risk evaluation results of the typical mines of Luan mining area

由表4可知：漳村矿和五阳矿的地质灾害危险性中等，王庄矿、常村矿和夏店矿的地质灾害危险性较轻。通过野外实地调查发现漳村矿和五阳矿由于采煤历史悠久、开采规模大、地质灾害分布较集中等特征使得该地区的地质灾害问题较周边煤矿突出，给当地人民的生活和生产带来了严重影响。因此，该评价结果与实地野外地质调查结果基本一致，从而佐证了改进突变级数法在矿山地质灾害危险性评价中的有效性。

3 结 语

在对潞安矿区地质灾害类型及特征分析的基础上，采用基于熵值法改进的突变级数法对该矿区5个典型矿井的地质灾害危险性进行了评价，并给出了最终的地质灾害危险性等级。结果表明：该评价结果与野外地质调查结果较吻合，对于矿山地质灾害危险性评价研究具有一定的参考价值。

[1] 杨梅忠，宋 丹，刘 飞，等.矿山地质灾害危险性评价[J].中国煤炭地质，2014，26(5)：45-47. Yang Meizhong,Song Dan,Liu Fei,et al.Mine geological hazard risk assessment[J].Coal Geology of China,2014,26(5)：45-47.

[2] 刘长春，郭付三，袁巧红，等.金属矿山地质灾害危险性区划研究[J].金属矿山，2010(6)：147-151. Liu Changchun,Guo Fusan,Yuan Qiaohong,et al.Research on hazard zonation of geological hazard of metal mines[J].Metal Mine,2010(6)：147-151.

[3] 吴安兵，郭 科，柳炳利.基于灰色-模糊理论的矿产资源地质勘查评价——以藏中地区为例[J].金属矿山，2015(3)：133-136. Wu Anbing,Guo Ke,Liu Bingli.Evaluation of geological exploration of mineral resources based on gray-fuzzy theory：a case study in Central Tibet[J].Metal Mine,2015(3)：133-136.

[4] 张 丽，李广杰，周志广，等.基于灰色聚类的区域地质灾害危险性分区评价[J].自然灾害学报，2009，18(1)：164-168. Zhang Li,Li Guangjie,Zhou Zhiguang,et al.Grey clustering method-based zoning assessment of regional geological disaster [J].Journal of Natural Disasters,2009,18(1)：164-168.

[5] 郭 彬，薛希龙，徐 敏.改进层次聚类法在矿山岩体分级中的应用[J].金属矿山，2011(11)：14-19. Guo Bin,Xue Xilong,Xu Min.Application of improved analytic hierarchy process-grey clustering method on mine rock mass classification[J].Metal Mine,2011(11)：14-19.

[6] 邓 辉，何政伟，陈 晔，等.信息量模型在山地环境地质灾害危险性评价中的应用[J].自然灾害学报，2014，23(2)：67-75. Deng Hui,He Zhengwei,Chen Ye,et al.Application of information quantity model to hazard evaluation of geological disaster in mountainous region environment[J].Journal of Natural Disasters,2014,23(2)：67-75.

[7] 张桂荣，陈丽霞，殷坤龙.浙江省永嘉县滑坡灾害危险性区划[J].水文地质工程地质，2005(3)：27-31. Zhang Guirong,Chen Lixia,Yin Kunlong.Landslide hazard zonation of Yongjia County,Zhejiang Province[J].Hydrogeology & Engineering Geology,2005(3)：27-31.

[8] 贾贵义，全永庆，黎志恒，等.基于组合赋权法的白龙江流域甘肃段地质灾害危险性评价[J].冰川冻土，2014，36(5)：1227-1234. Jia Guiyi,Quan Yongqing,Li Zhiheng,et al.Geo-hazards assessment for the Gansu Segment in Bailongjiang River Basin by using combination weighting method[J].Journal of Glaciology and Geocryology,2014,36(5)：1227-1234.

[9] 罗德江，吴尚昆，郭 科.基于组合权-灰色关联分析法的矿产资源开发利用综合评价[J].金属矿山，2015(2)：20-25. Luo Dejiang,Wu Shangkun,Guo Ke.The comprehensive evaluation of exploitation and utilization efficiency of mineral resources based on combination weight and gray relation analysis method[J].Metal Mine,2015(2)：20-25.

[10] 史冬梅，杨风暴，王肖霞.尾矿坝风险评估中指标相关性权重的确定[J].金属矿山，2014(11)：143-146. Shi Dongmei,Yang Fengbao,Wang Xiaoxia.Determining of correlation weights of index in tailing dam risk assessment[J].Metal Mine,2014(11)：143-146.

[11] 黄岑丽.潞安矿区煤炭开采对地质环境影响的研究[D].北京：中国矿业大学(北京)，2013. Huang Cenli.Study of the Impacts to Geological Environments by Coal Mining Activities in Luan Mining Area[D].Beijing ：China University of Mining and Technology(Beijing),Beijing,2013.

[12] 王 洋，马施民，安俊元，等.潞安矿区地面塌陷发育特征与危险性评价[J].能源环境保护，2014，28(4)：54-57. Wang Yang,Ma Shimin,An Junyuan,et al.Ground subsidence development characteristics and risk assessment in Luan mining area[J].Energy Environmental Protection,2014,28(4)：54-57.

[13] 张我华，王 军，张林柱，等.灾害系统与灾变动力学[M].北京：科学出版社，2011. Zhang Wohua,Wang Jun,Zhang Linzhu,et al.Disaster and Catastrophe Dynamics System[M].Beijing：Science Press,2011.

[14] 候造水，贾明涛，陈 娇.基于突变级数法和主成分分析法的长沙市生态安全评价[J].安全与环境学报，2015，15(2)：364-369. Hou Zaoshui,Jia Mingtao,Chen Jiao.Ecological security evaluation of Changsha City via analyzing the catastrophe progression and the principal component analysis method[J].Journal of Safety and Environment，2015,15(2)：364-369.

[15] 尚志海，蔡文慧，欧先交，等.基于突变理论的梅州市地质灾害灾度评估[J].安全与环境工程，2014，21(3)：55-59. Shang Zhihai,Cai Wenhui,Ou Xianjiao,et al.Geological hazard degree assessment of Meizhou City based on catastrophe theory[J].Journal of Safety and Engineering,2014,21(3)：55-59.

[16] 高振兴，赵江平，郭进平，等.基于突变理论的尾矿库安全评价[J].金属矿山，2009(12)：121-124. Gao Zhenxing，Zhao Jiangping，Guo Jinping,et al.Safety assessment of tailing pond based on catastrophe theory[J].Metal Mine,2009(12)：121-124.

[17] 陈红江，李夕兵，高 科.突变级数法在采空区塌陷预测中的应用[J].安全与环境学报，2008,8(6)：108-111. Chen Hongjiang，Li Xibing，Gao Ke.Application of catastrophe progression method in predicting the mining collapse accidents in goaf[J].Journal of Safety and Environment，2008,8(6)：108-111.

[18] 徐德宝，曹始友，徐孚效，等.基于突变理论的煤层底板突水危险性评价[J].煤矿安全，2014(12)：197-200. Xu Debao,Cao Shiyou,Xu Fuxiao,et al.Water inrush risk evaluation of coal seam floor based on catastrophe theory[J].Safety in Coal Mines,2014(12)：197-200.

[19] 郑德凤，臧 正，王平富.改进的突变模型及其在水资源评价中的应用[J].水利水电科技进展，2014，34(4)：47-49. Zheng Defeng,Zang Zheng,Wang Pingfu.An improved catastrophe model and its application in water resources assessment[J].Advances in Science and Technology of Water Resources,2014,34(4)：47-49.

[20] 宋小园，朱仲元，韩永明，等.基于改进的突变级数法在复垦区土壤恢复评价中的应用[J].干旱区地理，2014，37(5)：1012-1017. Song Xiaoyuan，Zhu Zhongyuan，Han Yongming,et al.Soil recovery evaluation based on catastrophe theory of reclamation soil[J].Arid Land Geography，2014,37(5)：1012-1017.

(责任编辑 王小兵)

Mine Geological Disaster Risk Evaluation Based on the Improved Mutation Progression Method：A Case Study in Luan Mining Area

Wang Yang Ma Shimin Xu Ke

(CollegeofGeoscienceandSurveyingEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)

In order to avoid the deficiencies of the calculation of evaluation index weight and subjective weight assignment of the classical mine geological disaster risk evaluation methods,taking Luan mining area as the study example,a improved mutation progression method based on entropy value method is proposed,and the improved mutation progression method is adopted to conduct mine geological disaster risk evaluation.Based on the systemic analysis of the characteristics and types of mine geological disasters in Luan mining area systematically,the five typical mines of Luan mining area are taken as the specific study examples,firstly,according to the characteristics and types of the mine geological disasters in Luan mining area,the index system of mine geological disaster risk evaluation is established,secondly,the relative importance of the same layer index of mine geological disaster risk evaluation is determined by adopting the entropy value method;then,the total mutations membership values of difference mines are calculated by the normalization formula of mutation progression method;finally,the mine geological disaster risk evaluation is conducted by adopting the converted graded standard.The evaluation result show that the mine geological disaster risk evaluated method proposed in this paper not only can avoid the subjectivity of determining the weights,but also can quantitatively distinguish the importance of the same level index,the evaluation results is consistent to the the filed geological investigation results,it can provide scientific basis for the risk evaluation and effective prevention and treatment of mine geological disaster.

Mine geological disaster,Risk evaluation,Entropy value method,Mutation progression method,Geological disaster type,Evaluation index system,Mutations membership value

2015-08-17

山西省矿业权价款地质勘查项目(编号：2009-070)。

王 洋(1987—)，男，博士研究生。通讯作者 马施民(1962—)，男，副教授，博士，硕士研究生导师。

TD167

A

1001-1250(2015)-11-164-05