降雨入渗条件下粗粒排土场稳定性分析
李 超 马淑芝 贾洪彪 李天慈
(中国地质大学工程学院,湖北 武汉 430074)
降雨入渗条件下粗粒排土场稳定性分析
李 超 马淑芝 贾洪彪 李天慈
(中国地质大学工程学院,湖北 武汉 430074)
基于饱和-非饱和渗流有限元分析,研究山西某矿区粗粒排土场在降雨条件下的入渗机理与特点。在对不同期矿渣排土体采样筛分的基础上,通过粒径分布曲线推导非饱和渗透系数,结合工程实例,运用Geostudio建立一定降雨强度条件下的边坡岩土体渗流场有限元分析模型,定量分析降雨过程对粗粒排土场稳定性的影响。结果表明:粗粒排土场因其粒径及结构上的特殊性,致使基质吸力随饱和度的变化趋势并不显著。前期排土体具有更好的压实作用,导致降雨入渗在排土体体内主要以渗透系数较大的第三期矿渣排土体为主,同时,排土体中通畅的渗流通道容易引起局部水力梯度值迅速攀升,又因为其排水过程较快,使排土场安全系数的滞后性并不明显,在雨后短时间内有所回升。
排土场 降雨入渗 非饱和理论 边坡稳定
排土场是一种特殊的人工边坡,具有结构松散,孔隙度大,颗粒级配较差,无黏聚力等特点,且不同期排土体具有不同的压实度,在稳定性分析上有别于一般边坡。传统的饱和-非饱和渗流理论主要应用于粉土及粉质黏性土边坡,而在矿区排土场人工边坡上的应用较少。本研究针对不同排土期、不同深度的排土体,在粒径筛分试验和饱水渗透试验基础上,将试验数据进行拟合,获取含水量-基质吸力曲线及非饱和渗透系数,并利用Geostudio分析了排土场的渗流场变化过程与稳定性,为工程实践提供参考。
1 饱和-非饱和渗流理论
在非饱和土中,单元体的含水量随空间和时间而发生变化,根据质量守恒原理,水的损失量或补给量等于水流入和流出土体单元的净流量,因此对于一般土体,瞬态非饱和三维流微分方程可表示为[1]
(1)

在饱和土中,总水头考虑重力水头、压力水头和流速水头,即发生降雨入渗时,饱和土的瞬态三维流微分方程可表示为[2]
(2)
式中,μ为流速;g为重力加速度;p为压力水头;kx,ky,kz为饱和渗透系数。
2 参数的获取
2.1 体积含水量函数
体积含水量函数是瞬态渗流分析的一个重要参数。由于直接通过试验方法获取该函数比较复杂,需要专门的试验设备,成本高,耗时长,并且在采用常规方法应用于粗粒结构土样时产生的误差较大。因此通过标准方法获取粒径分布曲线,利用拟合参数的闭合解来确定含水量函数曲线[3-6]。
加拿大学者Aubertin等[3-7]确立了一种根据粒径分布计算体积含水量的方法,该方法可以更好地表示从硬质岩分离出尾矿类材料的特征。该函数主要为2项饱和度的叠加:第1项是在较小负孔隙水压力下,由于毛细作用储蓄的水量;第2项是在较大负孔隙水压力下,由于吸附作用储蓄的水量。可以通过分析材料的孔隙率、颗粒形状和粒径来获取这2个参数。其公式如下:
(3)

毛细饱和度贡献量主要受孔隙大小和形状的影响,可表示为
(4)
式中,m为拟合参数,可以通过孔隙尺寸分布加以考虑;对于塑性黏土,m和a值均被认为是常量,其中m=3×10-5,a=7×10-4,而对于毛细土,m和a分别取1和0.01;hco为平均毛细上升高度;ψf为基质吸力。
2.2 渗透系数函数
土的导水能力在饱和-非饱和条件下,可以通过渗透系数函数来直观反映。在实际工程应用中,通过试验直接测量非饱和渗透系数所需费用高,周期长,因此可以通过建立的渗透系数函数,来简化计算。在饱和状态下,颗粒间所有孔隙被水充填;而在非饱和状态下,孔隙中包含部分空气,气体所占据的体积为渗流的非传导通道,导致渗流路径更加曲折,使整体渗透系数减小。因此可以断定,含水量是渗透系数的主要影响因素之一。
加拿大专家Fredlund[8]通过测量或估算的体积含水量函数和饱和渗透系数,来预测非饱和渗透系数函数。该方法表达式如下:
(5)
式中,ks为测得的饱和渗透系数;kw为计算所得的非饱和渗透系数;θs为饱和体积含水量;i为j到N之间的数值间距;y为代表负孔隙水压力计算方法的虚拟变量;j为最终函数描述的最小负孔隙水压力;N为最终函数描述的最大负孔隙水压力;ψ为对应第j步的负孔隙水压力;θ′为方程起始值。
3 工程实例
3.1 工程概况
某矿排土场所属矿区处于五台山中西段北麓,峨河中游南部中高山区,峨河流经矿区东北缘。区域地层以五台群地层为主体,主要有五台群石咀亚群金岗库组、庄旺组、文溪组。总容量6 010万m3,年排土量1 300万t。排土场的岩石松散体是由采场剥离的角闪片岩、云母石英片岩、绿泥角闪片岩等组成,平均松散系数为1.5。排土场地基上部为第四系残坡积土,主要为粉黏土,可塑~硬塑状态,局部含有碎石,厚度1~3m不等;出露的基岩主要为云母石英片岩,局部为角闪岩侵入体,岩石较坚硬。
矿区属温暖带季风型气候,四季分明,春季干旱多风,夏季东南季风盛行。区内降雨量在时空、强度分布上极不均匀,多年平均降水量为491.3mm(1957—2014年),最大年降水量为707.5mm(1964年),最小年降水量为276.5mm(1972年)。月最大降水量为330.5mm(1967年8月),日最大降雨量为100.4mm(1959年7月21日),最大时降雨量为50.1mm(1979年6月30日),最大半小时降雨量为41.7mm(1979年6月30日),降雨集中在6—9月份,约占全年降水量的75%。降雨强度表现为山区大、平原区小的特点,大气降水多以暴雨为主。
3.2 滑坡渗流场分析及稳定性计算
根据排土场具体工程地质条件,通过Geostudio的渗流模块SEEP/W,选取排土场主滑动方向上的典型剖面,建立边坡渗流场数值模型。剖面选取如图1所示。

图1 排土场剖面
有限元剖分边界条件设置为:①当降雨强度小于表层土体渗透系数时,边坡表层按流量边界条件处理,取值为降雨强度;当雨量大于表层土体渗透系数时,一部分雨水沿坡面流失,此时边坡表层按定水头处理。②模型两边为定水头边界条件。③模型底部为不透水边界条件。④由于该模型主要分析粗粒排土场在降雨条件下的渗流情况,因此基岩部分设置为不透水层。
对排土场不同部位进行取样分析,具体取样点位置如表1所示,通过粒径分析获取物料粒度组成曲线,见图2。
表1 取样点位置
Table 1 Sampling points m

取样编号排土场高程取样点高程取样点在排土场位置PNS18161636底PES17001420底1740m17401675中1720m17201720顶PE16841404底1588m15881505顶

图2 物料粒度组成曲线
依据Aubertin等前人的理论,通过粒径分布及孔隙度计算出含水量与基质吸力之间的函数曲线,如图3所示;通过Fredlund方法,将体积含水量函数和饱和渗透系数进行拟合,来预测非饱和渗透系数函数,其渗透系数与基质吸力之间的函数曲线如图4所示。
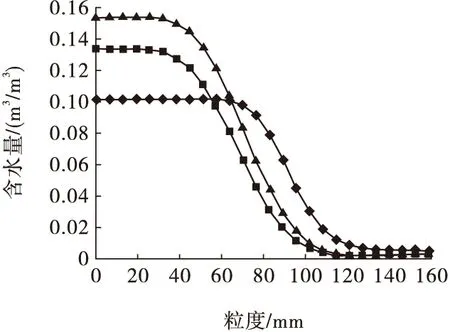
图3 含水量基质吸力曲线
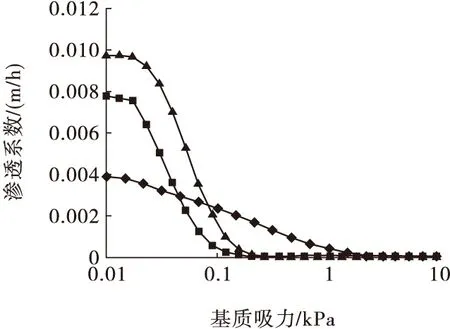
图4 渗透系数基质吸力曲线
根据矿区多年降雨观测数据,确定降雨强度为100 mm/d(极端工况),降雨持续时间24 h,降雨停止后入渗仍在进行,本次计算时间延长至120 h。分析共分为10个步时,通过模拟分别获得12、24、36、48、60、72、84、96、108、120 h时孔隙水压力分布图,并结合极限平衡法计算出最危险滑动面的安全系数。计算过程中,岩土体物理力学参数如表2。

表2 岩土体物理力学参数
4 计算结果分析
(1)渗流场分析。通过SEEP/W有限元程序进行非饱和渗流计算,该模拟分别给出降雨12、24 h及雨后60、120 h的孔隙水压力等值线图(见图5)。在等值线图中,孔隙水压力为零的区域处于暂态滞水状态,正值为饱和区,负值为非饱和区。

图5 孔隙水压力等值线(单位:kPa)
在降雨强度为100 mm/d,连续降雨12 h时(排土场孔隙水压力分布如图5(a)所示),降雨入渗过程中,边坡表层形成一个暂态饱和区,主要集中在坡肩后缘部分。降雨持续到24 h时,边坡表层孔隙水压力不断增加,暂态饱和区逐渐下移,坡肩和坡肩后缘部分暂态饱和区相互贯通,形成渗流主通道。至雨后60 h时,(孔隙水压力分布图如图5(c)),渗流仍在持续进行,孔隙水压力降低,局部坡面出现负孔隙水压力,坡面与坡肩后缘部分的渗流主通道被坡肩隔断,在坡面和坡肩内层分别形成暂态饱和区。至雨后120 h时,孔隙水压力持续降低,坡肩后援及斜坡内层暂态饱水区逐渐缩小,且主要分布在第三期排土层内。
(2)稳定性分析。利用非饱和土抗剪强度理论,通过Morgenstern-Price法分析降雨过程中边坡瞬态稳定性,由于该排土场具有良好的渗流通道,径流通畅,因此安全系数滞后性较小。通过模拟分析可知:安全系数随着降雨的持续不断降低;至雨后60 h时,达到最小值;在此之后,安全系数随着时间的增加而缓慢升高。其安全系数与降雨时间关系如图6所示。

图6 时间-安全系数曲线
由图6可知:初始条件下,排土场安全系数为1.456,稳定性较好。在降雨入渗过程中,随着含水量不断增加,导致孔隙水压力增大和基质吸力减小,边坡潜在滑动面抗剪强度减小,边坡的安全系数降低。降雨24 h时,排土场安全系数为1.189;降雨停止后,渗流继续进行,边坡安全系数持续降低,至雨后60 h时,边坡安全系数达到最小值1.024。排土场通过不断渗流和排水作用,边坡中上部孔隙水压力逐渐降低,边坡表层的暂态饱和区逐渐减小,基质吸力增加,边坡潜在危险滑动面的抗剪强度增大,边坡安全系数缓慢上升。但由于排水不够彻底,坡体内仍存在一定范围的饱水区域,因此边坡的安全系数在短期内不能恢复至初始值。
5 结 论
(1)降雨入渗使粗粒排土场体内饱水区域迅速增加,并不断下移扩散,排土体自重增大;基质吸力减小,抗剪强度降低;在含水量和基质吸力共同作用下,边坡体稳定性下降。
(2)在粗粒排土场降雨入渗过程中,坡肩区域率先进入饱水状态,并逐渐向边坡后缘和坡面发展,形成浅表层饱水区域,因此在降雨入渗过程中坡肩处稳定性最差。
(3)通过模拟计算,降雨强度为100 mm/d,连续降雨24 h时,安全系数为1.189;至雨后60 h时,降低至最小值;在此之后,安全系数随着时间的增加而缓慢升高,但在短期内不能恢复至初始值。根据饱和-非饱和土理论,由于排土场具有良好的渗流通道,因此在降雨和雨后排水过程中安全系数滞后性不明显。
[1] 吴长富,朱向荣,依小涛,等.强降雨条件下土质边坡瞬态稳定性分析[J].岩土力学,2008,29(2):33-37. Wu Changfu,Zhu Xiangrong,Yi Xiaotao,et al.Analysis of soil slope′s transient stability under intensive rainfall[J].Rock and Soil Mechanics,2008,29(2):33-37.
[2] 周家文,徐卫亚,邓俊华,等.降雨入渗条件下边坡的稳定性分析[J].水利学报,2008,39(9):1066-1073. Zhou Jiawen,Xu Weiya,Deng Junhua,et al.Stability analysis of slopes under rainfall infiltration[J].Journal of Hydraulic Engineering,2008,39(9):1066-1073.
[3] Aubertin M,Mbonimpa M,Bussiere B,et al.A model to predict the water retention curve from basic geotechnical properties[J].Canadian Geotechnical Journal,2003,40(6):1104-1122.
[4] 徐 晗,朱以文,蔡元奇,等.降雨入渗条件下非饱和土边坡稳定分析[J].岩土力学,2005,26(12):1957-1962. Xu Han,Zhu Yiwen,Cai Yuanqi,et al.Stability analysis of unsaturated soil slopes under rainfall infiltration[J].Rock and Soil Mechanics,2005,26(12):1957-1962.
[5] 林鸿州,于玉贞,李广信,等.降雨特性对土质边坡失稳的影响[J].岩石力学与工程学报,2009,28(1):198-204. Lin Hongzhou,Yu Yuzhen,Li Guangxin,et al.Influence of rainfall characteristics on soil slope failure[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):198-204.
[6] Ning Lu,Willian J Likos.非饱和土力学[M].韦昌富,译.北京:高等教育出版社,2012. Ning Lu,Willian J Likos.Unsaturated Soil Mechanics[M].Wei Changfu,translated.Beijing:China High Educational Press,2012.
[7] 潘建平,刘湘平,王宇鸽,等.饱和尾矿稳态特征研究[J].金属矿山,2014(1):145-149. Pan Jianping,Liu Xiangping,Wang Yuge,et al.Study on steady-state properties of saturated tailings[J].Metal Mine,2014(1):145-149.
[8] 郑禄璟,郑禄琳,常晓娜,等.露天边坡稳定性影响因素分析及防治措施[J].金属矿山,2014(2):131-136. Zheng Lujing,Zheng Lulin,Chang Xiaona,et al.Influencing factor analysis and control of open pit slope stability[J].Metal Mine,2014(2):131-136.
(责任编辑 徐志宏)
Stability Analysis of Coarse Grain of Dumping Under the Condition of Rainfall
Li Chao Ma Shuzhi Jia Hongbiao Li Tianci
(CollegeofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China)
Based on saturated-unsaturated seepage finite element theory,the infiltration mechanism and characteristics of coarse grain of dumping under the condition of rainfall analysis in a mining area in Shanxi were investigated.On basis on the sieving test of slags in different dumping period,the unsaturated permeability coefficient was derived through particle size distribution curve.Combined with an engineering example,and with use of the numerical simulation software Geostudio,the finite element model of slope seepage was established,and quantitative analysis on the effect of rainfall stage on for coarse mine stability was made.Results showed that the particularity size and structure of the coarse grain mine results that the change trend of matric suction along with saturation is not significant.While,the previous dump has a better compactness,and the rainfall seepage mainly comes to the third period of dumping with a greater hydraulic conductivity.At the same time,the unobstructed seepage channel in dump can easily cause a local rapid rise in hydraulic gradient,and also because of its fast drainage process,the stability coefficient of coarse mine has a not obvious lagging.But in a short time after the rain,it will have a certain amount of rebound.
Dumping site,Rainfall infiltration,Unsaturated theory,Slope stability
2015-07-24
国家自然科学基金项目(编号:50908217)。
李 超(1990—),男,硕士研究生。
TD12
A
1001-1250(2015)-09-147-05

