基于岭回归与灰色耦合模型的建设用地规模预测——以河南省焦作市为例

余长坤，宋文博，吴次芳，范慧萍

(1.浙江大学公共管理学院，杭州310029;2.河南农业大学资源与环境学院，郑州450002)

改革开放以来，中国城市建设用地面积迅速扩张，土地供需矛盾日益严重。由于建设用地利用方式存在难以逆转的特性，为保障土地资源的可持续利用、防止建设用地的无序蔓延，在土地利用时，必须有效地对建设用地规模进行预测和合理规划［1］。建设用地总量预测的方法有很多，其中常用到的有时序预测、回归模型法等回归分析模型［2］。多元回归分析一般是使用OLS模型，但是模型中的自变量往往存在多重共线性，构建的模型存在缺陷往往使预测结果不尽人意［3-4］。

处理多重共线性常用的方法有逐步回归、主成分回归和岭回归等，但当共线性较为严重时，逐步回归和主成分分析自动筛选变量的方法通常会损失某些重要信息［5］。岭回归虽然是有偏估计，但是却能很好地控制回归系数的标准误差大小，通过减少OLS估计中由于共线性而产生的方差，来从根本上消除数据共线性的影响［6-7］;而且岭迹法的应用能够融入人的主观能动性［8-9］，将定性分析和定量分析结合应用。目前，岭回归在经济、生态和医学领域上得到了广泛应用，如李名峰［10］应用岭回归方法，实证研究了土地要素对经济增长的贡献;朱勤等［11］从消费压力和人口的视角，运用岭回归方法计量分析人口、消费和技术因素对碳排放的影响;郑照宁等［12］用岭回归方法建立了一个包括资本、劳动和能源在内的经济生产函数;彭海艳等［13］采用一阶广义差分法和岭回归法，建立了医疗卫生费用的供给和需求模型，并进行了实证分析。

未来10年内，焦作市仍处于经济发展和城市化进程的快速发展阶段。伴随着经济转型，焦作市各种建设活动将陆续展开，必定增加对建设用地的需求，建设用地和耕地的矛盾将进一步加大［14］。对焦作市建设用地规模合理预测，不但能为土地利用总体规划实现途径提供科学支撑，而且能保障土地资源可持续利用［15-16］。本研究在运用因子分析和主成分分析进行影响因子共线性诊断的基础上，尝试引入岭回归方法建立建设用地规模预测模型，并选择相应的驱动因子建立灰色预测模型，对未来建设用地规模进行预测，旨在为以后的更为深入的研究提供参考。

1 焦作市概况与建设用地动态分析

焦作位于河南省西北部，北倚太行与山西接壤，南临黄河与郑州、洛阳相望。位于东经112°02'～113°38'，北纬34°48'～35°30'，总面积为4 071 km2。2010 年末全市总人口354.30万人，地区生产总值1 245.93亿元。

焦作是一座典型的因煤而起的城市，早在建国初期，就以煤炭产业为基础形成了比较完善的工业体系;到了1995年，仅资源型企业生产产值就占全市工业总值的90%以上。然而，焦作也是一座典型的因煤而困的城市，随着煤矿资源的日益衰竭，加上企业设备老化造成开采成本增加，资源型企业效益下滑，逐渐使焦作经济陷入困境;到1999年，全市国民生产总值和财政收入分别下滑13%和24%，城市命运也与资源行业一损俱损。自身的经济危机也为焦作市的城市转型提供了契机，2008年4月正式被国务院列为“资源枯竭型城市”转型试点［17］。

2002年以来，焦作市工业化水平大幅提高，经济得到飞速发展，建设用地面积呈现出逐年上升趋势(图1)。建设用地增长大体可以分为2个阶段:2002—2008年间建设用地增长较慢，建设用地7年共计增长了55.15 km2，年平均增长率为1.46%;2008—2010年建设用地增长加快，这期间建设用地总共增长115.46 km2，年平均增长率为8.45%，增量明显高于前一阶段。

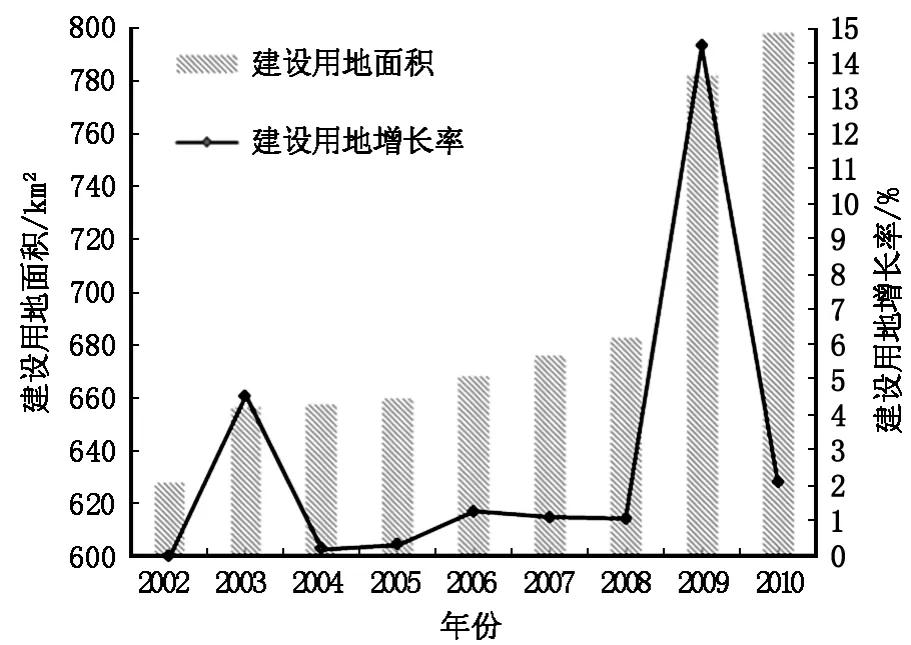
图1 焦作市建设用地规模变化趋势及增长率Fig.1 Land use change trend and growth rate in Jiaozuo City

2 研究方法

为提高预测模型的精度，去除最小二乘估计不能克服的共线性问题，本研究选用岭回归对建设用地规模的回归模型进行参数修订，并通过灰色GM(1，1)对岭回归模型的自变量分别进行建模预测，尝试探讨一种有效且精度更高的建设用地规模预测方法。

2.1 岭回归原理

岭回归是在 20世纪 70年代由 A.E.Hoerl等［6］提出，是一种从根本上消除数据共线性的统计学方法。当自变量间存在多重共线性时，矩阵X'X行列式比较小，甚至趋近于0，此时矩阵在计算时得到的数据往往缺乏稳定性和可靠性。岭回归通过在样本数据矩阵加上一个正常数矩阵k I(0＜k＜1，I为单位矩阵)，以牺牲很小精度的代价换取估计结果稳定性的大幅提高［18-20］。岭回归虽然是有偏估计，但其得到的模型参数在稳定性能上明显高于OLS回归模型。在实际应用中，岭参数k值的确定是岭回归方法的关键。通常是采用岭迹图法［21］，即对每个自变量xi，绘制随k值变化的岭回归估计值的变化曲线图，一般选择k值应使各自变量的岭迹趋于稳定。

2.2 GM(1，1)模型原理

灰色预测是以GM(1，1)模型为主而进行的预测。通过对离散地，包含不确定变动因素的数据进行累加或者累减处理，使其变成有较为明显规律的系统，最后建立系统变动规律的相应微分方程，来预测系统未来的发展趋势［22-23］。

式中:-a是发展指数;b是灰色作用量。x(1)的灰色预测模型为:

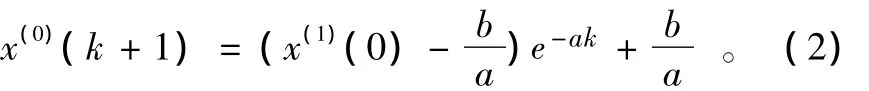
从而得到原始数据序列:

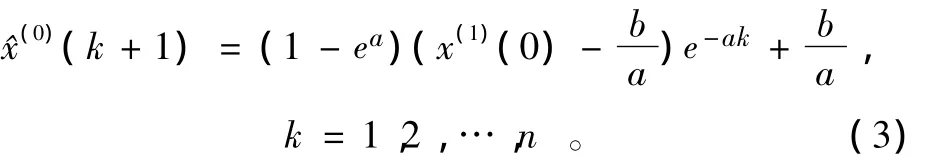
式中:^x是发展指数。

3 结果与分析

影响建设用地变化的因素很多，根据数据的可获得性，结合已有研究［24-28］以及焦作市建设用地变化特征，最终筛选确定了总人口x1(万人)、地区生产总值x2(亿元)、第一产业所占比x3(%)、建筑业所占比例x4(%)、全社会固定资产投资总额x5(亿元)、公共设施用地面积x6(km2)、公路里程x7(km)共7个因子构建驱动因子指标体系。

3.1 数据共线性诊断

估计模型之前，首先分析建设用地与驱动力因子之间的关系以及驱动力因子之间的相关程度。利用EViews 6.0软件SCAT和COR命令得到相关系数矩阵(表1)。

表1 焦作市建设用地与各驱动因子相关系数矩阵Tab.1 The correlation matrix of construction land change and driving factors in Jiaozuo City

从表1看出，除x3，x4，x7之外，其他因子均与建设用地面积高度相关，而且驱动因子之间也普遍存在两两高度相关关系。为进一步检验驱动因子之间的相关关系，用驱动因子相关系数矩阵的特征值进行检验［29］。求取主成分特征值，并计算X'X，发现标准化后的样本数据矩阵是病态矩阵，病态指数值为138.60(远大于30)。样本数据存在着严重多重共线性，此时如果采用最小二乘估计模型，将使各因子的系数均方误差变大，出现某些因子回归系数的符号与实际不符，或者很重要的解释变量的回归系数检验不显著等情况。为克服共线性的影响，改用岭回归估计方法来修正模型。

3.2 岭回归模型分析

运用SPSS 19.0岭回归函数，对数据处理，得到7个驱动因子的岭迹图(图2)。由图2可以看出，k从0开始略有增加时，x4的岭回归系数显著地下降，而且迅速趋于零，失去预测能力，首先剔除;x2和x5岭回归系数之和大体上稳定，且x5与其他因子的相关系数较大，考虑剔除x5。用y与其余的5个因子作岭回归，并把岭参数步长改为0.05，范围减少到0.8，得到5个驱动因子的岭迹图(图3)。

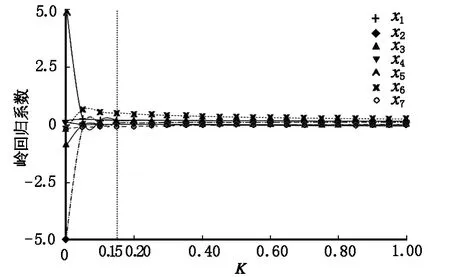
图2 焦作市影响建设用地变化的7个驱动因子的岭迹图Fig.2 The 7 driving factors of the ridge trace plot changes related to the construction land in Jiaozuo City

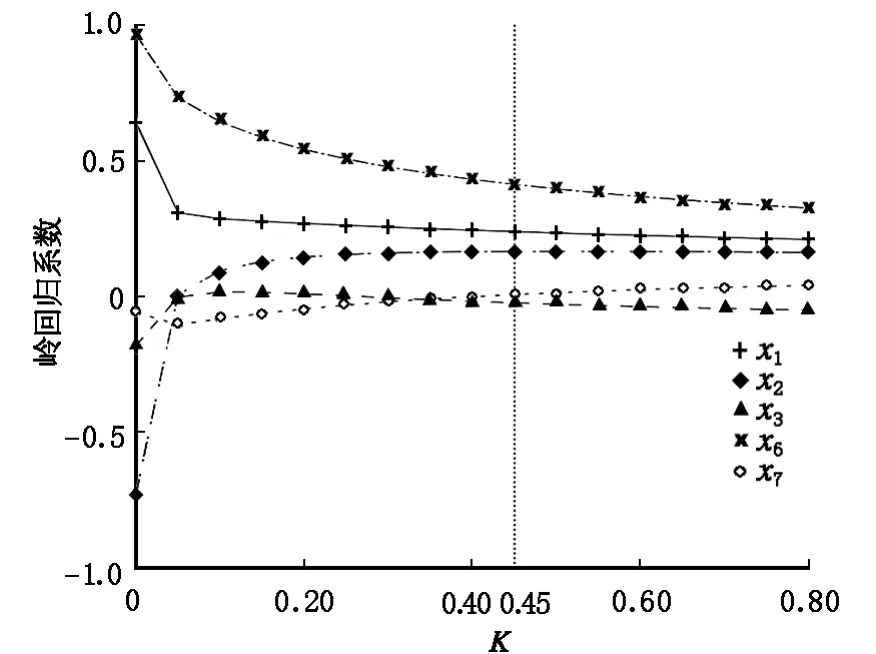
图3 焦作市影响建设用地变化的5个驱动因子的岭迹图Fig.3 The 5 driving factors of the ridge trace plot changes related to the construction land in Jiaozuo City

对保留的5个影响因子作主成分分析，计算斜差阵的特征根得出前3个主成分的贡献累计达到91%以上，说明选用变量可以很好地解释建设用地规模的变化。从图3可以看出，剔除x4，x5后岭回归系数变化幅度变小，岭参数k在0.40～0.50之间时，岭回归系数已经基本稳定，选取k=0.45得到岭回归方程:

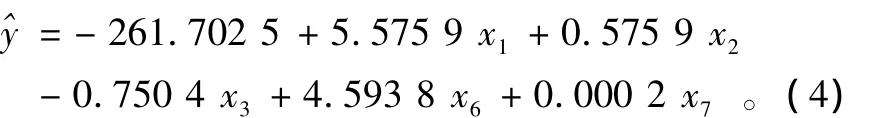
结合焦作市 x1，x2，x3，x6和 x7的历史数据对焦作市建设用地规模进行拟合。计算预测精度评价指标值MAPE(mean absolute percentage error)仅为 1.909 ＜10，说明模型的预测精度较高，预测值很好地拟合了历史数据。其中2008年预测结果的相对误差较大，这与国务院在2008年将焦作市划定为经济转型试点有很大关系。在种种政策鼓励下，焦作市开始由“煤矿城市”向“优秀旅游城市”、“黑色印象”向“绿色主题”的转型，其旅游业大力发展的同时，有利地带动了住宿餐饮业和公共设施管理业等第三产业的快速发展与繁荣，致使建设用地规模出现明显波动。

由式(4)可知，5个影响因子中，对建设用地规模影响最大的是公共设施用地面积(0.413)，其次分别是总人口(0.239)、地区生产总值(0.165)、第一产业所占比例(0.024)和公路里程(0.007)，这与多数人［30-33］的研究结论相似，与吴建寨等［34］研究结果存在着明显不同，也说明不同区域之间社会经济发展模式存在着差异;建设用地规模与公共设施用地面积、总人口、地区生产总值和公路里程呈正相关关系，与第一产业所占比例呈负相关关系;公共设施用地面积、总人口、地区生产总值和公路里程每增加或减少1个单位，将分别引起建设用地规模增加或减少 0.413，0.239，0.165，0.007 个单位;第一产业所占比例每增加或减少1个单位，建设用地规模将减少或增加0.024个单位。

3.3 GM(1，1)模型预测分析

采用GM(1，1)模型对影响建设用地规模的驱动因子进行短期预测，得出5个驱动因子的灰色模型(表2)。结合式(4)最终得出建设用地规模近年的预测值(表3)。从表3可以看出，焦作市建设用地规模在短期内将保持稳定增长，到2015年达到923.06 km2。为对比研究结果，继续采用灰色预测法单独对建设用地规模进行预测，并分别计算3种预测模型的相对偏差(图4)。由图4可见，相比岭回归模型和灰色预测模型，耦合模型精度更高，能更好反映出焦作市建设用地规模变化情况。

表2 焦作市建设用地规模驱动因子GM(1，1)预测模型Tab.2 The GM(1，1)forecast model of construction land change driving factors of Jiaozuo City

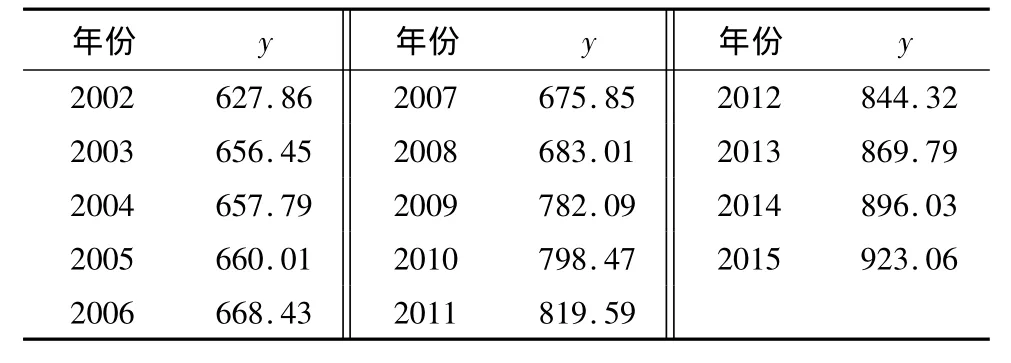
表3 建设用地规模岭回归－灰色预测结果 km2Tab.3 Ridge-grey prediction results of construction land scale

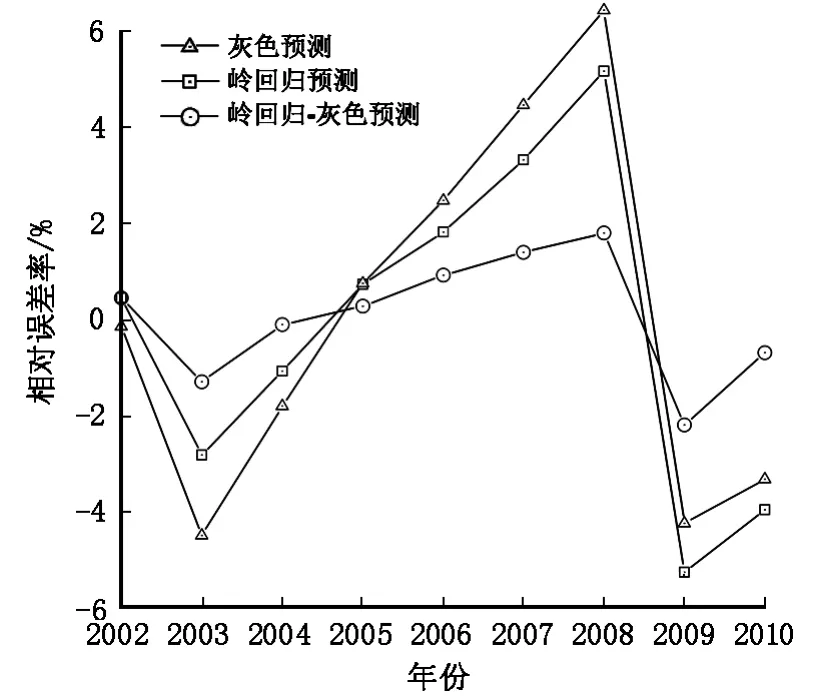
图4 建设用地规模预测模型相对误差Fig.4 The prediction results and the relative error of construction land scale

4 结论与建议

4.1 结论

1)影响建设用地变化的驱动因子之间存在数据关联性，引入岭回归可以很好地解决驱动因子的共线性问题，且参数估计的显著性和稳定性明显高于普通回归，MAPE仅为1.909。由岭回归模型的预测结果可以看出，用岭回归只需要选取较少的驱动因子建立模型即可，并且模型的分析效果比较理想。

2)在影响焦作市建设用地规模变化的5个驱动因子中，公共设施用地面积、总人口、地区生产总值和公路里程与建设用地规模呈正相关关系，第一产业所占比例与建设用地规模呈负相关关系，对建设用地规模影响作用强度为公共设施用地面积＞总人口＞地区生产总值＞第一产业所占比例＞公路里程。

3)灰色预测对于含有不确定信息的系统预测具有较大的优势，能在保证较高预测精度的前提下较好地反映系统的实际情况。相对于岭回归模型和灰色预测模型，将两种模型进行耦合能得到精度更高、拟合结果更为理想的建设用地规模预测值。最终预测结果显示焦作市建设用地规模在近期内将保持稳定增长，到2015年达到 923.06 km2。

4.2 建议

1)公共设施用地面积对焦作市建设用地规模变化的影响最大，其驱动作用远大于第一产业所占比例和公里里程。2008年之后，焦作市公共设施用地面积出现飞跃式增长，3年间增加了7 km2。虽然公共设施事业的发展有助于焦作市改变“黑色印象”，但是当地政府应该对公共设施建设项目进行专家论证和严格的审批。可以适度超前发展基础设施，增强经济转型基础能力支撑，同时，也要注意防止过度占用土地，坚决杜绝重复性建设或过度建设而浪费土地的现象。

2)人口数量是影响建设用地规模的重要因素。虽然焦作市实行严格的计划生育政策，但近期内焦作市城镇化水平将会持续增加，大量农村人口流入城市，政府应适时开展建设用地增减挂钩和社会主义新农村建设试点，减少农村建设用地土地资源浪费，提高全市建设用地的人口承载力。

3)城镇产业集聚和产业结构演变对建设用地规模的增加有着巨大影响。焦作市应该继续挖掘新的经济增长点，及时优化和升级产业结构。地方政府应该转变绩效考核的模式，把工作重点放到提高经济增长的质量和效益上来，把经济发展建立在严格控制建设用地规模的基础上。

［1］ 穆向丽.小城镇建设用地需求预测研究——以广东省阳山县为例［D］.武汉:华中农业大学，2007.

［2］ 郭杰，欧名豪，刘琼，等.基于BP神经网络的南通市建设用地需求预测［J］.资源科学，2009，31(8):1355-1361.

［3］ 杨杰，吴中如.观测数据拟合分析中的多重共线性问题［J］.四川大学学报:工程科学版，2005，37(5):19-24.

［4］ 田一梅，汪泳，迟海燕.偏最小二乘与灰色模型组合预测城市生活需水量［J］.天津大学学报，2004，37(4):322-325.

［5］ 官建成，王晓静.中国对外直接投资决定因素研究［J］.中国软科学，2007，25(2):59-65.

［6］ Hoerl A E，Kennard R W.Ridge Regression:Biased Estimation for Nonorthogonal Problems［J］.Technometrics，1970，12(1):55-67.

［7］ 姚珊珊，魏法杰.基于岭回归法的工业产品成本预测模型［J］.辽宁工程技术大学学报:自然科学版，2008，27(6):937-940.

［8］ 孙海玲，王红平.基于岭回归的城市建筑能耗增长驱动因素研究［J］.城市发展研究，2013，20(5):21-24.

［9］ 杨丽霞.基于C-D函数和岭回归的粮食生产影响因素分析——以浙江省为例［J］.地域研究与开发，2013，32(1):147-150.

［10］ 李名峰.土地要素对中国经济增长贡献研究［J］.中国地质大学学报:社会科学版，2010，10(1):60-64.

［11］ 朱勤，彭希哲，陆志明，等.人口与消费对碳排放影响的分析模型与实证［J］.中国人口·资源与环境，2010，20(2):98-102.

［12］ 郑照宁，刘德顺.考虑资本—能源—劳动投入的中国超越对数生产函数［J］.系统工程理论与实践，2004，24(5):51-54.

［13］ 彭海艳，伍晓榕.中国医疗卫生费用增长的实证分析［J］.经济与管理，2006，20(9):13-16.

［14］ 冯晓华.中国资源型城市旅游业可持续发展探析——以焦作市为例［J］.资源开发与市场，2009，25(5):460-463.

［15］ 吕志强，白杨，丁喜莲，等.城市建设用地与其影响因子的定量分析——以山东省即墨市为例［J］.国土资源科技管理，2005，22(3):53-56.

［16］ 彭保发，胡曰利，吴远芬，等.基于灰色系统模型的城乡建设用地规模预测——以常德市鼎城区为例［J］.经济地理，2007，27(6):999-1002.

［17］ 陈俊杰，李新泉，刘玲玲.对煤炭资源型焦作市可持续发展的探索与实践［J］.中国矿业，2008，17(8):43-45.

［18］ Zhang Y，Wang L，Zhang H，et al.An Analysis on Land Use Changes and Their Driving Factors in Shule River:An Example form Anxi County［J］.Progress in Geography，2003，22(3):270-278.

［19］ 陈莉.基于岭回归和支持向量机结合的数据挖掘新方法［J］.情报学报，2008，27(2):229-234.

［20］ Christensen L R，Jorgenson DW，Lau L J.Transcendental Logarithmic Production Frontiers［J］.The Review of Economics and Statistics，1973，55(1):21-26.

［21］ 叶斌，程茂吉，张媛明.城市总体规划城市建设用地适宜性评定探讨［J］.城市规划，2011，35(4):41-48.

［22］ 钱吴永，党耀国，刘思峰.含实践幂次项的灰色GM(1，1，t～ α )模型及其应用［J］.系统工程理论实践，2012，32(10):2247-2252.

［23］ 邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1990:1-12.

［24］ 王枫.城市建设用地需求量预测模型研究［D］.哈尔滨:哈尔滨工程大学，2007:36-37.

［25］ 许婧婧，陶文星，包广静，等.我国特大城市建设用地影响因素的地区差异［J］.经济地理，2006，26(12):152-156.

［26］ 吕晓，黄贤金，钟太洋，等.建设用地扩张过程的时间均衡态势分析［J］.农业工程学报，2013，29(15):236-243.

［27］ Holz CA.New Capital Estimates for China［J］.China E-conomic Review，2006，17(2):142-185.

［28］ 李宾，曾志雄.中国全要素生产率变动的再测算:1978—2007年［J］.数量经济技术经济研究，2009，20(3):3-15.

［29］ 赵卫亚.计量经济学教程［M］.2版.上海:上海财经大学出版社，2010:118-121.

［30］ 朱家彪，杨伟平，粟卫民.基于多元逐步回归与通径分析的临澧县建设用地驱动力研究［J］.经济地理，2008，28(3):488-491.

［31］ 陈春，冯长春.中国建设用地增长驱动力研究［J］.中国人口·资源与环境，2010，20(10):72-78.

［32］ 吕可文，苗长虹，安乾.河南省建设用地扩张及其驱动力分析［J］.地理与地理信息科学，2012，28(4):69-74.

［33］ 钱宏胜，梁留科，王发曾.中部六省城市体系规模序列研究［J］.地域研究与开发，2007，26(2):56-61.

［34］ 吴建寨，彭涛，徐海燕，等.山东省建设用地扩展时空动态及驱动力分析［J］.中国人口·资源与环境，2011，21(8):164-169.