层流波动区膜状凝结雷诺数关系式对传热计算的影响

吴 磊，刘 洋，贾海军，马喜振

（清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084）

膜状冷凝传热是一个复杂且经典的传热问题，吸引了众多研究者对其进行研究，为核能工程、化学工程、航空航天等众多领域的工程应用奠定了坚实的基础。膜状冷凝传热的复杂性体现在：热力学非平衡态特性、不同的冷凝传热条件、蒸汽和液膜流型的复杂性、壁面几何结构和冷凝介质的多样性等［1］。

当前对膜状冷凝传热研究主要是基于Nusselt膜状冷凝传热理论［2］的理论改进和实验验证。在理论方面，主要包括对过冷度、液膜的温度修正以及惯性力和拖拽力等方面影响的考虑［3-5］。近些年来，特别针对具有非凝结性气体存在条件下的膜状冷凝传热问题进行了深入的研究［6-8］。在实验方面，众多研究者通过实验对Nusselt膜状冷凝传热理论进行了验证，并在光滑层流区域得到较好吻合；由于具有非凝结性气体存在的冷凝传热的应用广泛，众多的研究者对具有非凝结性存在条件下的膜状冷凝传热进行了大量的实验研究［9-12］。另外，Butterworth通过大量的实验研究，根据雷诺数将液膜划分为光滑液膜层流、有波动的液膜层流和湍流3个区域，并给出了相应的传热关系式［13］。

很多传热关系式的选择或修正项的给出均是基于雷诺数的，所以雷诺数的定义和计算对传热系数的计算具有重要的影响。雷诺数的定义具有基于质量和能量关系的两种方式，这两种定义方式分别是雷诺数基本定义的衍生。当前，对于二者之间的差别和使用范围无明确的界定，以至于部分研究者将二者在所有范围内等同使用［7，12］，从而造成一定的误差。在中低压情况下，液膜的流动主要集中在光滑液膜层流和有波动的液膜层流区域，以及考虑到传热修正式的简单性（湍流情况下包含普朗特数），本文重点关注光滑液膜层流和有波动液膜层流区域。

本文主要针对管外纯蒸汽自然对流膜状冷凝传热，分别基于质量和能量关系定义雷诺数，通过与光滑液膜层流区和有波动的液膜层流区传热关系式联立，求解得到传热系数和雷诺数理论解，并着重分析两种雷诺数关系式以及对应的传热系数在不同流动区域内的关系。通过与实验结果比较，检验两种雷诺数定义的适用性，并从物理模型方面给出解释。

1 膜状冷凝传热理论模型

膜状冷凝传热理论是根据Nusselt首次提出的光滑层流冷凝传热模型［2］发展的。基于Nusselt膜状冷凝理论，Butterworth发展提出了有波动液膜层流流动以及液膜湍流流动的传热关系式［13］。

光滑液膜层流区域（Re≤30），应用Nusselt液膜传热方程：

式中：hfilm为液膜传热系 数；ρl 为液膜密 度；ρg为水蒸气密度；g 为重力加速度；h′fg为修正的汽化潜热；kl为液膜导热系数；μl 为液膜黏度；L 为冷凝壁面长度；Ti为界面温度；Tw为壁面温度。

引入雷诺数，可得到光滑液膜层流区域Nusselt液膜传热方程的另一种表达式：

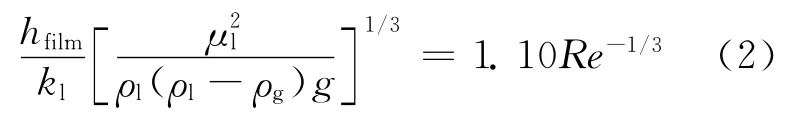
有波动液膜层流区域（30＜Re≤1 600），Butterworth传热关系［13］的传热系数修正项为0.8（Re／4）0.11，基于式（1）、（2）分别得到两种有波动液膜层流区域的传热系数表达式：

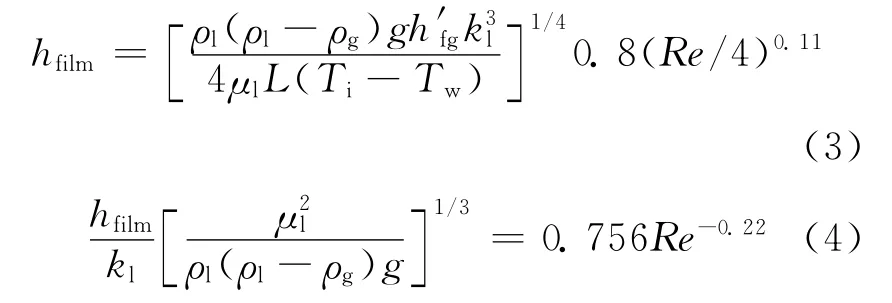
在实验研究及工程应用中，多涉及平均传热系数。在整个雷诺数范围内，采用积分平均方法求得平均传热系数：

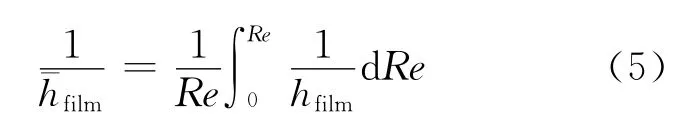
式中，¯hfilm为平均传热系数。

得到不同区域的液膜平均传热系数如下：

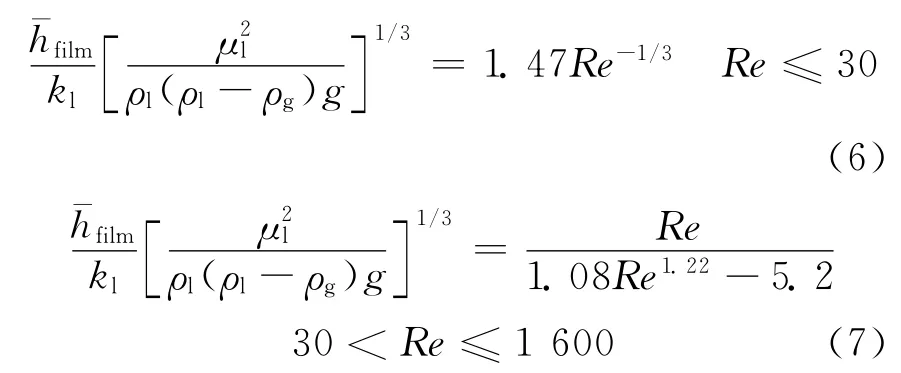
考虑凝结过冷度和液膜界面温度跳跃，h′fg采用如下修正式［14］：

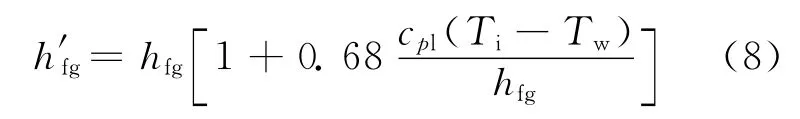
式中：cpl为液膜比定压热容；hfg为汽化潜热。

计算冷凝液膜物性参数的特征温度Tfilm定义为：

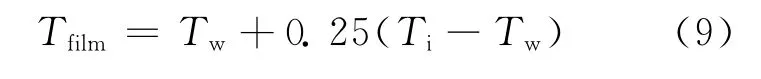
2 膜状冷凝传热雷诺数的定义

在膜状冷凝传热中，由雷诺数原始定义分别基于能量和质量关系衍生出两种表达方式，二者主要差别是基于不同的方式对质量冷凝率进行计算。

对于管外冷凝传热问题，雷诺数原始定义为：

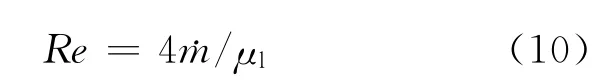
式中，˙m 为质量冷凝率。

在实验中，˙m 是可测量的；但在理论分析中，˙m 需通过计算得到。

根据Nusselt膜状冷凝传热理论和质量关系计算得到˙m：

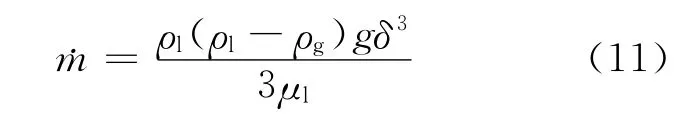
式中，δ为液膜厚度。

将式（11）代入式（10）可得基于质量关系的雷诺数Remass表达式：

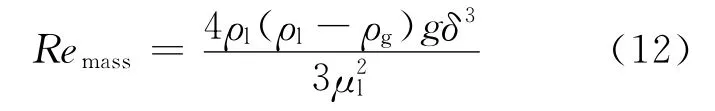
基于能量关系计算得到˙m 为：

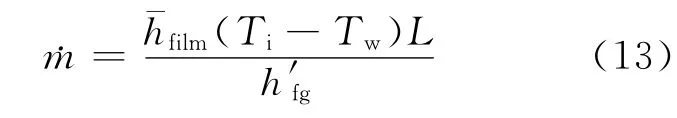
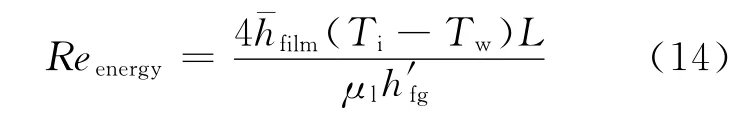
3 理论分析

为进一步研究两种不同雷诺数关系式的差别及影响，分别选用不同雷诺数关系式和不同流动区域内的传热关系式联立求解，最终得到基于基本参数的雷诺数表达式，并分析雷诺数关系式对传热系数的影响。

3.1 光滑液膜层流区

选用基于能量关系的雷诺数定义和平均传热关系式，联立式（6）和式（14），则光滑液膜层流区基于能量关系的雷诺数可表示为：

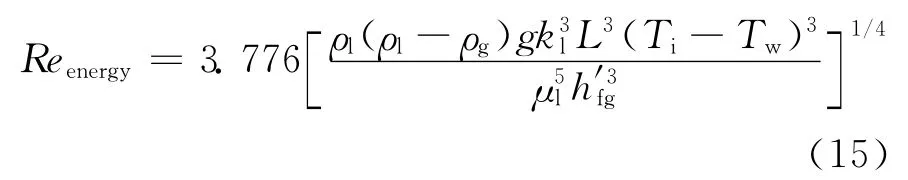
选用基于质量关系的雷诺数定义和局部传热关系式，联立式（1）和式（12），则光滑液膜层流区基于质量关系的雷诺数可表示为：

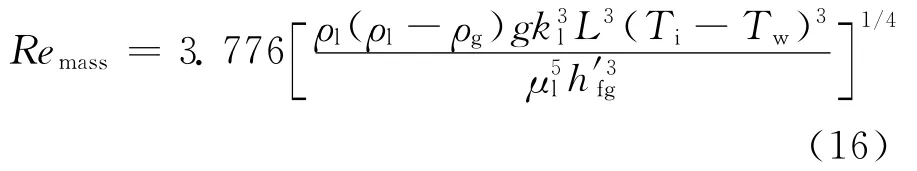
比较式（15）和式（16），可得Remass和Reenergy在光滑液膜层流区是等价的。

根据式（6）可知，在光滑层流区域内，传热系数计算结果也是相等的。

3.2 有波动液膜层流区

选用基于能量关系的雷诺数定义和平均传热关系式，联立式（7）和式（14），则有波动液膜层流区基于能量关系的雷诺数可表示为：

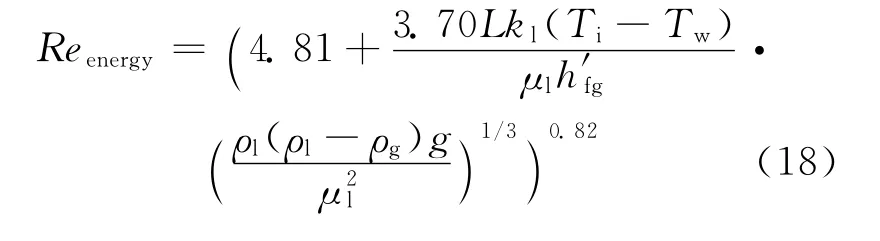
选用基于质量关系的雷诺数定义和局部传热关系式，联立式（3）和式（12），则有波动液膜层流区基于质量关系的雷诺数可表示为：

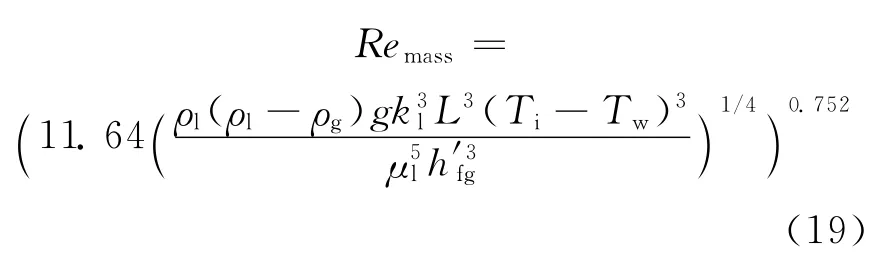
联立式（18）和式（19），可得到Remass和Reenergy在有波动液膜层流区的关系（图1）：

大数据又称巨量资料（big data），指的是所涉及的资料量规模巨大到无法透过目前主流软件工具，在合理时间内达到撷取、管理、处理并整理成为帮助企业经营决策更积极目的的资讯。

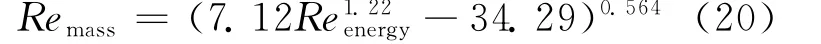
从图1 可看出，在有波动液膜层流区内，Reenergy约为Remass的1～4倍。

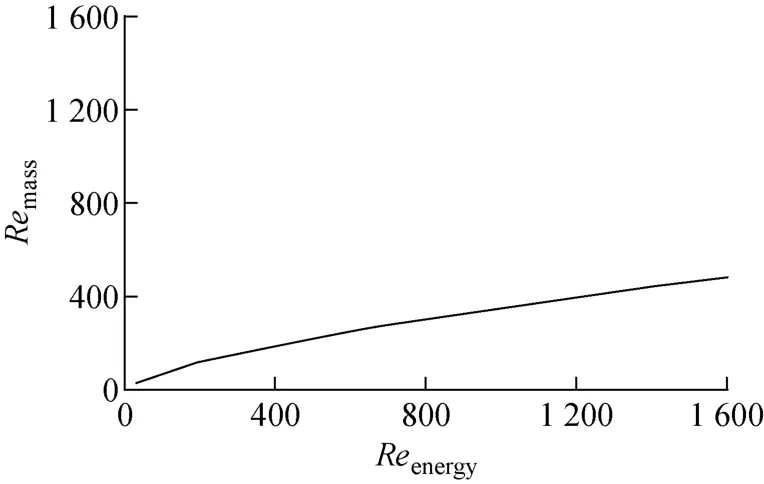
图1 有波动的层流区域内Remass与Reenergy的关系Fig.1 Relation between Remassand Reenergy in laminar and wavy flow region

3.3 雷诺数定义对传热系数的影响

根据式（20）得到Reenergy与Remass的关系，并联立式（7）在有波动液膜层流区域内计算平均传热系数的关系式，可得到基于Reenergy与Remass计算得到的平均传热系数的关系，且定义：

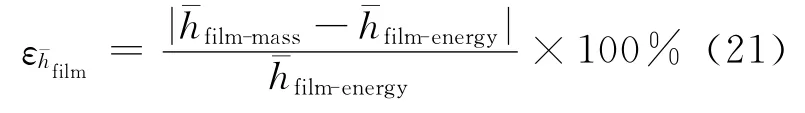
从图2可看出，在有波动层流区域内平均传热系数的相对偏差随Reenergy的增大不断增加，最大的相对偏差出现在Reenergy＝1 600，对应ε¯hfilm＝30.3%。

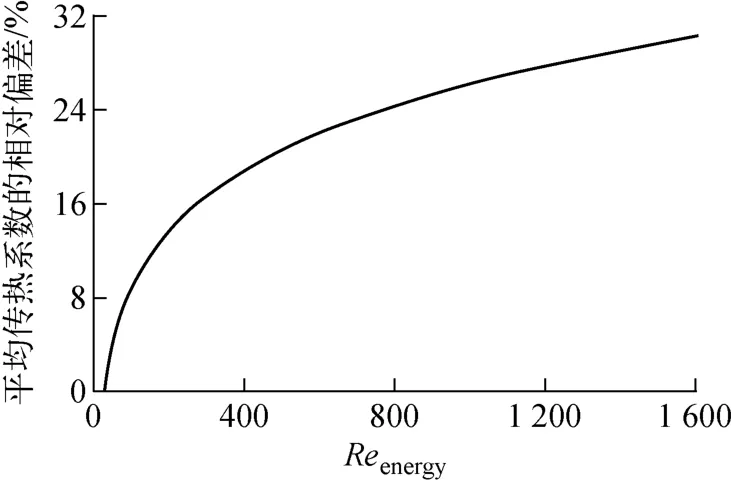
图2 有波动的层流区域内平均传热系数的相对偏差Fig.2 Relative deviation of average heat transfer coefficient in laminar and wavy flow region

4 实验分析

为进一步分析雷诺数关系式的差别和验证雷诺数关系式对传热系数的影响，选择Chung等［11］的实验进行比较，关注于短板上纯蒸汽自然对流膜状冷凝传热。实验条件列于表1。

表1 实验条件Table 1 Experiment condition

图3示出了基于不同雷诺数关系式计算得到的热流密度随气相空间与壁面温差ΔTwb的变化。从图3 可看出，在整个实验范围内，基于Reenergy计算得到的热流密度和实验数据吻合最好，特别是在较大气相空间和壁面温差条件下。基于Remass计算得到的热流密度出现过度预测现象，计算值平均超过实验结果约10%。相反地，Nusselt膜状冷凝理论预测的结果小于实验值，且与实验结果的偏差随气相空间和壁面温差的增加而增大。当气相空 间 和 壁 面 温 差 较 小（ΔTwb＜16 K）时，Nusselt膜状冷凝理论可较好地预测实验结果，而基于Reenergy计算得到的热流密度出现小幅的过度预测，此时主要因为对应的雷诺数小于80，液膜表面的波动状况较弱，Nusselt膜状冷凝理论在此范围仍适用。

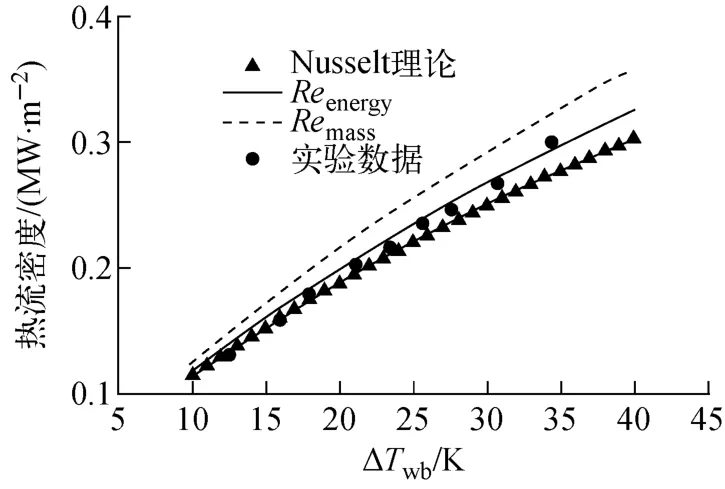
图3 热流密度随ΔTwb的变化Fig.3 Heat flux density vs.ΔTwb

5 讨论与分析

基于上述分析，液膜传热系数的计算是通过联立求解得到的。不同雷诺数定义不仅对膜状冷凝传热系数产生影响，且会对雷诺数自身的计算产生重要影响。从实验结果的对比可知，Reenergy具有较好的适用性。此部分主要从物理模型方面进行讨论。

基于质量的雷诺数Remass定义涉及到液膜厚度的计算，且液膜厚度计算方式如下：

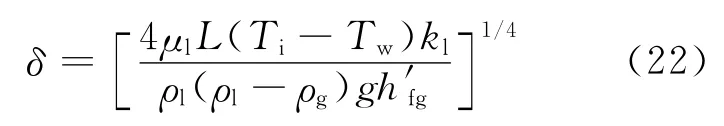
液膜厚度与局部液膜传热系数的关系式通过以下方程进行关联：

式（22）、（23）均是基于液膜是光滑的假设。在光滑液膜层流区域内，液膜是光滑的，所以两种雷诺数关系式是等价的。当液膜出现波动时，液膜厚度的计算和液膜与局部传热关系式的关系只是近似表达式，且会将误差引入到对雷诺数以及传热系数的计算中。基于传热系数和热传导率计算液膜厚度计算的方式不能直接扩展应用于有波动液膜层流区域。

基于能量的雷诺数Reenergy，不涉及液膜厚度的计算，完全基于能量平衡，从而在整个流型区域内均可应用。

6 结论

本文主要研究了雷诺数关系式对纯蒸汽自然对流膜状凝结传热系数在光滑层流和有波动层流区域的影响，主要结论如下：

1）基于质量和能量定义雷诺数，并通过与光滑液膜层流区和有波动的液膜层流区的传热关系式联立求解，得到分别基于基本参数的Reenergy和Remass的表达式。

2）在光滑液膜层流区域，基于质量和能量关系得到的雷诺数具有等价性，且对应平均传热系数相等，在有波动液膜层流区域，基于能量得到的Reenergy约为基于质量得到的Remass的1～4倍，且计算得到的平均传热系数最大相对偏差约为30.3%，对液膜流型的判定及传热系数的计算具有较大影响。

3）液膜厚度计算方法的超范围应用是在有波动的液膜层流区域内产生误差的主要原因，通过实验和理论分析，基于能量关系的Reenergy计算传热系数具有更高的准确性，并推荐使用。

［1］ ROSE J W.Condensation heat transfer fundamentals［J］.Chemical Engineering Research and Design，1998，76（2）：143-152.

［2］ NUSSELT W.The condensation of steam on cooled surface［J］.Journal of the Association of German Engineers，1916，60：541-546，569-575.

［3］ ROHSENOW W H.Heat transfer and temperature distribution in laminar film condensation［J］.Transactions of the American Society of Mechanical Engineers，1956，78：1 645-1 648.

［4］ SPARROW E M，GREGG J L.A boundary-layer treatment of laminar film condensation［J］.J Heat Transfer Series C，1959，81：13-18.

［5］ MINKOWYCZ W J，SPARROW E M.Condensation heat transfer in the presence of non-condensables，interfacial resistance，superheating，variable properties and diffusion［J］.Int J Heat Transfer，1966，9：1 125-1 144.

［6］ KIM M H，CORRADINI M L.Modeling of condensation heat transfer in a reactor containment［J］.Nuclear Engineering and Design，1990，118：193-212.

［7］ HERRANZ L E，ANDERSON M H，CORRADINI M L.A diffusion layer model for steam condensation within the AP600containment［J］.Nuclear Engineering and Design，1998，183：133-150.

［8］ CARUSO G，MAIO D V D.Heat and mass transfer analogy applied to condensation in the presence of non-condensable gases inside inclined tubes［J］.Int J Heat Mass Transfer，2014，68：401-414.

［9］ DEHBI A A.The effect of non-condensable gases on steam condensation under turbulent natural convection conditions［R］.US：Massachusetts Institute of Technology，1991.

［10］ANDERSON M H，HERRANZ L E，CORRADINI M L.Experimental analysis of heat transfer within the AP600containment under postulated accident conditions［J］.Nuclear Engineering and Design，1998，185：153-172.

［11］CHUNG B J，KIM M C，AHMADINEJAD M.Film-wise and drop-wise condensation of steam on short inclined plates［J］.Journal of Mechanical Science and Technology，2008，22：127-133.

［12］WONKIM J，GUNLEE Y，KYOUNAHN H，et al.Condensation heat transfer characteristic in the presence of non-condensable gas on natural convection at high pressure［J］.Nuclear Engineering and Design，2009，239：688-698.

［13］GENGEL Y A.Heat transfer：A practical approach［M］.New York：MaGraw-Hill，1997.

［14］COLLIER J G，THOME J R.Convective boiling and condensation［M］.3rd ed.Oxford：Oxford University Press，1994.