多物理耦合分析自动建模软件SuperMC/MCAM5.2设计与实现
吴宜灿,俞盛朋,程梦云,宋 婧,何 桃,郝丽娟,胡丽琴,龙鹏程,罗月童,汪 冬,甘 佺,王 文,吴 斌,董 良,杨 琪
(中国科学院 核能安全技术研究所,中国科学院 中子输运理论与辐射安全重点实验室,安徽 合肥 230031)
对多种物理过程如热交换、热对流、电磁传播和粒子输运等的耦合过程进行精确模拟计算需基于CAD模型建立统一几何的计算模型。这些物理计算模型的几何主要包含两类:有限元计算程序的网格模型和基于蒙特卡罗方法的粒子输运程序的构造几何(CSG)模型。目前已存在多种基于CAD 技术的网格建模工具,如ANSYS[1]、ATTILA[2]、SALOME[3]和ABAQUS[4]。而目前公开发布并获得广泛使用的基于CAD 的CSG 自动建模程序仅多物理耦合分析自动建模软件SuperMC/MCAM(multi-physics coupling analysis modeling program)[5-7],它是FDS 团队遵循先进软件研发过程[8]研发的超级蒙特卡罗核计算仿真软件系统SuperMC[9]的建模模块。该软件实现了基于CAD 的蒙特卡罗自动建模方法,已成功应用于聚变概念堆[10]、聚变裂变混合堆[11]、聚变堆包层[12-13]、铅基裂变堆[14]研究中,并成功完成了多项ITER 任务[15-16]。
各蒙特卡罗程序的开发目的和应用领域不同,被广泛应用于探测器设计、聚变堆设计、裂变堆设计、医学物理等领域。这些不同的应用领域中,模型的几何具有不同的特点,相应的蒙特卡罗计算包含了不同的建模需求,传统手工建模难以进行不同领域的蒙特卡罗建模。CAD 是通用的几何表达方式,各领域均使用它进行工程设计,因此需要基于CAD模型进行不同应用领域的蒙特卡罗程序建模。不同的蒙特卡罗计算程序的应用间存在交集,程序因数据库和物理处理方法等不同致使计算结果存在差异,需基于统一的计算模型进行不同蒙特卡罗程序间的计算结果对比。多蒙特卡罗计算程序间的结果对比可用于验证计算结果,确保计算分析的正确性。同时在蒙特卡罗程序的开发中,与公认的蒙特卡罗计算程序的计算结果对比也是验证新开发蒙特卡罗程序正确性的重要手段[17]。
本文发展的SuperMC/MCAM5.2 版本,实现基于CAD 的SuperMC、MCNP[18]、FLUKA[19]、Geant4[20]和TRIPOLI[21]自动建模,同时实现多蒙特卡罗程序计算模型互转功能。本文将介绍SuperMC/MCAM5.2的最新研发进展以及其新功能的测试验证。
1 SuperMC/MCAM5.2功能简介
SuperMC/MCAM5.2 主 界 面 如 图1 所示,其主要功能包括几何建模、几何转换、物理建模。其中,几何建模功能包括基本几何体创建、预处理模型等功能;物理建模功能包括对材料、源、计数的向导式创建;几何转换功能由正向转换和反向转换组成。正向转换功能可实现从CAD 模型向基于面描述及实体描述的蒙特卡罗计算模型几何的转换,可快速建立复杂的蒙特卡罗计算模型。反向转换功能可实现蒙特卡罗模型几何和材料等信息到CAD 模型的转换,可有效检查蒙特卡罗几何模型和材料信息。

图1 SuperMC/MCAM5.2主界面Fig.1 Main interface of SuperMC/MCAM5.2
在几何转换功能上,SuperMC/MCAM5.2在MCNP[5]、TRIPOLI[22]建 模 功 能 的 基 础 上新研发了SuperMC、FLUKA、Geant4 建模技术,新技术使SuperMC/MCAM 能支持多种蒙特卡罗软件的建模,实现多蒙特卡罗程序计算模型互转,成为基于CAD 的多蒙特卡罗自动建模软件。
2 多蒙特卡罗建模方法
2.1 多蒙特卡罗几何正向转换技术
CAD 模型常用边界表示法(boundary representation,BREP)表示,按照体、面、环、边的层次描述几何。而蒙特卡罗程序由于输运计算的要求,均采用CSG 方法描述几何。在MCNP、FLUKA 等 蒙 特 卡 罗 程 序 中,CSG 方法使用基于平面、二阶曲面(柱面、锥面、球面、双曲面、抛物面)以及特殊高阶曲面(圆环面)的半空间描述几何。在Geant4 等蒙特卡罗程序中,CSG 以任意方向、任意位置的基本体(长方体、圆柱体、圆环、圆椎体、球等)及其布尔运算方式描述几何。SuperMC 采用混合半空间与基本体的描述方法,其中布尔运算可同时作用于半空间与基本体上,实现自由度更高的模型建模。
SuperMC/MCAM5.2实现了从BREP 到CSG 的模型转换技术,从而实现了CAD 模型到多种蒙特卡罗模型的正向转换。BREP 到CSG 的转换过程如图2 所示,过程为:1)将BREP实体分解为一个或多个凸实体;2)将凸实体分解为面的集合,使用面构成的半空间的交集描述凸实体;3)使用凸实体描述的并集描述BREP实体形成实体的CSG 树状表达方式;4)使用蒙特卡罗模型中的基本元素(如MCNP 中 的 半 空 间、SuperMC 和Geant4中的基本体、FLUKA 中的体素)描述CSG 模型中的半空间,进而输出不同蒙特卡罗的几何模型。
2.2 多蒙特卡罗几何反向转换技术
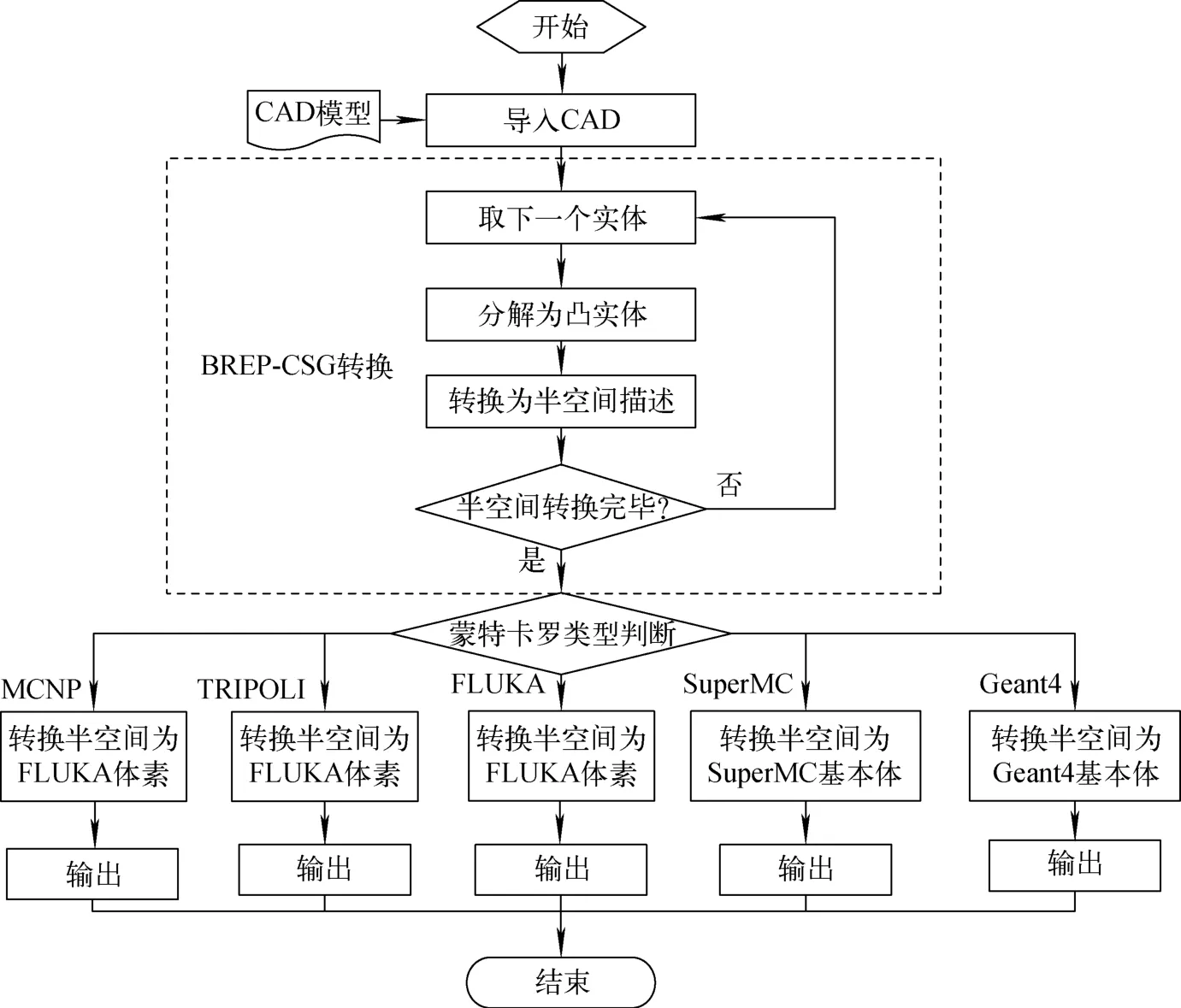
图2 SuperMC/MCAM5.2多蒙特卡罗转换流程Fig.2 Multi-Monte Carlo conversion progress of SuperMC/MCAM5.2
在SuperMC/MCAM 的反向转换模块中,蒙特卡罗计算模型中几何的表达式被解析为由基本体或半空间经过交、并、补运算形成的CSG 层次结构,成为CSG 树。每个几何实体对应一棵CSG树。CSG树的叶子节点是基本体或半空间,这些基本体和半空间首先被转换为CAD几何中对应的简单几何体,如平面半空间被构造为大的立方体,球面或球基本体被构造为球体,二次曲面通过解析相应转换为球体、圆柱体或圆锥体,特殊的四次曲面如圆环半空间转换为圆环体等;简单几何体通过交、并、补运算构造成叶子节点的父节点即CSG 几何形式中的基本的凸实体,构造完毕的非叶子节点成为新的叶子节点;迭代进行交、并、补运算直至CSG树根节点,形成CSG实体对应的CAD实体。
结合多蒙特卡罗正、反转技术,SuperMC/MCAM 以CAD 模型为桥梁实现了多蒙特卡罗程序计算模型互转功能。
3 测试验证
为验证新开发的SuperMC、FLUKA、Geant4自动建模功能,选择国际基准反应堆例题、FLUKA 与Geant4自带的测试例题开展大量体系化的测试。本文选取其中的ITER 基准模型的偏滤器模型,对多蒙特卡罗程序建模功能进行对比测试。
3.1 ITER 基准模型
ITER 基准模型是ITER 国际组织发布的ITER 装置中子学模型[15],其中的偏滤器模型包含509个栅元,2 990个面,是该模型中最为复杂的部件之一。图3为在SuperMC/MCAM中的ITER 基准模型与偏滤器模型。
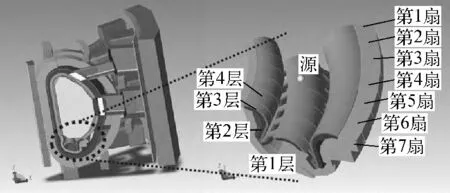
图3 ITER 基准偏滤器模型Fig.3 Divertor model in ITER benchmark
3.2 蒙特卡罗自动建模测试
本文采用输运计算验证通过SuperMC/MCAM 建立的SuperMC、FLUKA、Geant4计算模型的几何正确性。不同的蒙特卡罗计算程序使用不同的数据库且粒子物理处理方法不同,输运计算结果存在一定差别。通量是蒙特卡罗粒子输运计算的基本物理量,真空通量去除了材料、物理过程的影响,直接反映了蒙特卡罗计算模型几何的正确性。因此,本文为验证几何转换的正确性,进行了真空通量测试。在多蒙特卡罗建模中,由于SuperMC/MCAM 的MCNP自动建模功能已得到验证[9],其正确性已得到证实,因此多个蒙特卡罗之间的测试结果以MCNP的模拟结果作为基准。
计算的条件如下:1)所有栅元材料均赋以真空;2)靠近偏滤器中心上方的位置设一个14.00MeV 各向同性的中子点源;3)模拟的粒子数为1.0×108;4)根据模型中材料(分为4层)和部件的轴向分布(分为7扇),共分为28组,对这28组栅元分别统计粒子径迹长度。
图4 示 出 了SuperMC、FLUKA、Geant4与MCNP得到的粒子径迹长度计算结果的相对偏差,其中SuperMC 与MCNP 的相对偏差最大为5.232 563×10-6,平均为2.533 164×10-7;FLUKA 与MCNP 的 相 对 偏 差 最 大 为1.751 534×10-3,平均为4.209 053×10-4;Geant4与MCNP的相对偏差最大为2.773 268×10-3,平均为3.328 539×10-4。
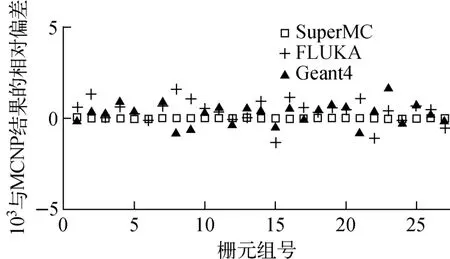
图4 不同蒙特卡罗模型的粒子径迹长度计算结果的相对偏差Fig.4 Relative deviation for particle track length calculation result of different Monte Carlo models
从以上结果可知,在SuperMC、FLUKA、Geant4等蒙特卡罗模型上计算的真空粒子径迹长度一致,证实了这些蒙特卡罗模型的几何一致性及SuperMC/MCAM 的多蒙特卡罗转换功能的正确性。
3.3 蒙特卡罗几何反转测试
在蒙特卡罗正向转换建模的正确性得到验证的基础上,本文进行蒙特卡罗几何反转的正确性测试。首先通过多种蒙特卡罗程序的正向转换得到不同蒙特卡罗的偏滤器模型,再由SuperMC/MCAM 中各蒙特卡罗程序反转模块反转得到对应的CAD 模型。经SuperMC/MCAM 可视化后,这些经不同蒙特卡罗正、反转模块得到的CAD 模型无可视化差别。本文统计了这些CAD 模型体积的偏差。相对于原始CAD 模型,各实体的相对体积偏差均小于0.000 1%,这与CAD 核心的容差限值10-6具有相同量级,对比结果证实了本文研发的蒙特卡罗几何反转功能的正确性。
3.4 蒙特卡罗几何互转测试
为验证SuperMC/MCAM 提供的多蒙特卡罗程序计算模型互转功能的正确性,本文进行图5 所示的MCNP 模型到多蒙特卡罗模型间转换的测试。使用了3.2 节中偏滤器第1次正转生成的MCNP模型,首先通过SuperMC/MCAM 将MCNP 模 型 反 向 转 换为CAD 几何,再通过SuperMC/MCAM 转换为SuperMC、FLUKA 和Geant4 模 型。最后,使用3.2 节中介绍的方法使用生成的SuperMC、FLUKA 和Geant4 模 型 进 行 真 空径迹长度对比。
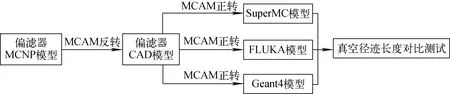
图5 蒙特卡罗模型间几何互转测试Fig.5 Testing of conversion among different Monte Carlo models
图6示出了各蒙特卡罗几何互转测试结果与原始MCNP计算结果的相对偏差,其中SuperMC与MCNP的相对偏差最大为4.917 26×10-6,平均为4.004 41×10-7;FLUKA 与MCNP的相对偏差最大为1.591 604×10-3,平均为4.209 315×10-4;Geant4 与MCNP 的 相 对 偏 差 最 大 为1.619 897×10-3,平均为3.430 510×10-4。原始MCNP模型经SuperMC/MCAM 转换后生成 的SuperMC、FLUKA 和Geant4 模 型 的计算结果仍与原始MCNP 计算结果吻合。证实了SuperMC/MCAM 的多蒙特卡罗程序计算模型互转功能的正确性。
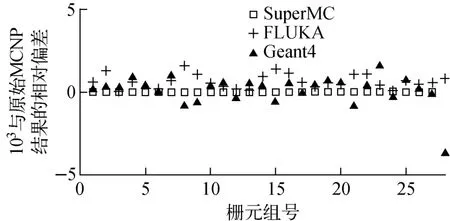
图6 蒙特卡罗互转测试与原始MCNP结果的对比Fig.6 Comparison of Monte Carlo conversion calculation results and MNCP result
对比本测试与第1次正转测试可看出,各蒙特卡罗在反转、正转前后的结果一致,证明经SuperMC/MCAM 正、反转后的CAD 模型无变化,证实了SuperMC/MCAM 多蒙特卡罗程序计算模型互转功能的正确性。
4 结论
多物理耦合分析自动建模软件SuperMC/MCAM5.2 可 支 持CAD 模 型 与SuperMC、MCNP、Geant4、TRIPOLI、FLUKA 等多种蒙特卡罗程序以半空间及基本体描述的计算几何之间的自动转换以及蒙特卡罗程序模型之间的自动转换。选取了ITER 基准模型等国际基准例题进行了系统的正确性测试,测试结果显示了SuperMC/MCAM5.2多蒙特卡罗自动建模功能的有效性与可靠性。
感谢FDS团队其他成员为本工作提供的各项帮助和支持。
[1] ANTONOVA E E,LOOMAN D C.Finite ele-ments for thermoelectric device analysis in ANSYS[C]∥24th International Conference on Thermoelectrics.Clemson:IEEE,2005.
[2] WAREING T A,MCGHEE J M,MOREL J E.ATTILA: A three-dimensional,unstructured tetrahedral mesh discrete ordinates transport code[J].Transactions of the American Nuclear Society,1996,75:146-147.
[3] SALOME[EB/OL].[2014-10-01].http:∥www.salome-platform.org.
[4] ABAQUS users'manual[M].France:Simulia Inc.,2006.
[5] WU Y.CAD-based interface programs for fusion neutron transport simulation[J].Fusion Engineering and Design,2009,84(7-11):1 987-1 992.
[6] 吴宜灿,李莹,卢磊,等.蒙特卡罗粒子输运计算自动建模程序系统的研究与发展[J].核科学与工程,2006,26(1):20-27.WU Yican,LI Ying,LU Lei,et al.Research and development of the automatic modeling system for Monte Carlo particle transport simulation[J].Chinese Journal of Nuclear Science and Engineering,2006,26(1):20-27(in Chinese).
[7] HU H,WU Y,CHENG M,et al.Benchmarking of SNAM with the ITER 3Dmodel[J].Fusion Engineering and Design,2007,82:2 867-2 871.
[8] 吴宜灿,胡丽琴,龙鹏程,等.先进核能软件发展与核信息学实践[M]∥中国科研信息化蓝皮书.北京:科学出版社,2013:232-244.
[9] WU Y,SONG J,ZHENG H,et al.CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC[J].Annals of Nuclear Energy,doi:10.1016/j.anucene.2014.08.058.[10]WU Y,FDS Team.Conceptual design activities of FDS series fusion power plants in China[J].Fusion Engineering and Design,2006,81(23-24):2 713-2 718.
[11]WU Y,QIAN J,YU J.The fusion-driven hybrid system and its material selection[J].Journal of Nuclear Materials,2002,307-311:1 629-1 636.
[12]WU Y,FDS Team.Design analysis of the China Dual-Functional Lithium Lead(DFLL)test blanket module in ITER[J].Fusion Engineering and Design,2007,82:1 893-1 903.
[13]CHEN Y,WU Y.Conceptual study on high performance blanket in a spherical Tokamak fusiondriven transmitter[J].Fusion Engineering and Design,2000,49-50:507-512.
[14]吴宜灿,柏云清,宋勇,等.中国铅基研究反应堆概念设计研究[J].核科学与工程,2014,34(2):56-63.WU Yican,BAI Yunqing,SONG Yong,et al.Conceptual design of China Lead-based Research Reactor CLEAR-Ⅰ[J].Nuclear Science and Engineering,2014,34(2):56-63(in Chinese).
[15]LI Y,LU L,DING A,et al.Benchmarking of MCAM 4.0with the ITER 3Dmodel[J].Fusion Engineering and Design,2007,82(15-24):2 861-2 866.
[16]王国忠,党同强,熊健,等.MCAM4.8 在ITER建筑大厅中子学建模中的应用[J].核科学与工程,2011,31(4):351-355.WANG Guozhong,DANG Tongqiang,XIONG Jian,et al.Application of MCAM4.8in creating neutronics model for ITER building[J].Chinese Journal of Nuclear Science and Engineering,2011,31(4):351-355(in Chinese).
[17]SONG Jing,SUN Guangyao,CHEN Zhenping,et al.Benchmarking of CAD-based SuperMC with ITER benchmark model[J].Fusion Engineering and Design,2014,89(11):2 499-2 503.[18]BRIESMEISTER J F.MCNP:A general Monte Carlo N-particle transport code,version 4C,LA-13709-M[M].US:LANL,2000.
[19]FASSO A,FERRARI A,RANFT J,et al.FLUKA: A multi-particle transport code,SLAC-R-773[M].Stanford:Stanford University,2005.
[20]AGOSTINELLI S,ALLISON J,AMAKO K,et al.Geant4:A simulation toolkit[M].Nucl Instrum Methods A,2003,506(3):250-303.
[21]BOTH J P,MAZZOLO A,PENELIAU Y,et al.User manual for version 4.3of the TRIPOLI-4 Monte-Carlo method particle transport computer code[M].France:CEA,2003.
[22]LU L,LEE Y K,ZHANG J,et al.Development of Monte Carlo automatic modeling functions of MCAM for TRIPOLI-ITER application[J].Nucl Instrum Methods A,2009,605(3):384-387.

