高速铁路无砟轨道温度场简化计算方法

欧祖敏，孙 璐，2，程群群

（1.东南大学 交通学院，江苏 南京210096；2.美国华盛顿Catholic大学 土木工程系，美国 华盛顿20064）

曝露于大气环境下的无砟轨道结构会遭受随外界环境温度变化而变化的温度荷载作用［1］，因对无砟轨道结构内部温度场变化规律知之有限，目前仅能考虑少数工况下的轨道结构温度作用效应［2-4］.在设计中难以完全反映轨道结构真正的温度荷载需求，给无砟轨道结构主要构件设计使用寿命不小于60 a的要求提出了挑战.

我国最新修订的建筑荷载规范指出结构的温度荷载应按热工学原理确定［5］，由于高速铁路无砟轨道结构温度变化受太阳辐射、气温、风速、降雨量和蒸发量等多种外界环境因素所影响，准确计算轨道结构内部温度场的难度较大.目前大多仅能通过现场实测来研究其变化规律［6-7］，但实测费时费力且代表性有限.因此，一种既简便又实用的轨道结构温度场计算方法显得非常必要.

根据热工学原理对曝露于大气环境下的无砟轨道结构温度场的计算方法开展研究.本文利用气象数据资料近似描述外界环境的主要影响因素以建立边界条件，提出一种简化的温度场计算方法.然后利用部分现场实测数据进行对比验证，并对轨道结构温度场变化规律进行分析.

1 无砟轨道结构温度场解析解

1.1 无砟轨道结构一维热传导方程

对带状无砟轨道结构，假设温度在平面内均匀分布，仅在深度方向存在温差，无砟轨道结构可近似理想化为一维传热问题.根据能量守恒定理，单位时间内出入轨道结构表面的热能变化率与通过表面单位距离内的热通量成正比，数学描述如下［8］：

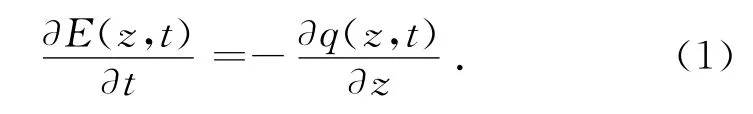
式中：E（z，t）为进入轨道结构的热能量，q（z，t）为轨道结构沿深度方向的热通量，z为轨道结构深度方向的坐标，t为时间.

傅里叶热传导定律认为温度场与热通量之间存在一定的关系，在一维热传导问题中，热通量与温度梯度存在如下比例关系［9］：

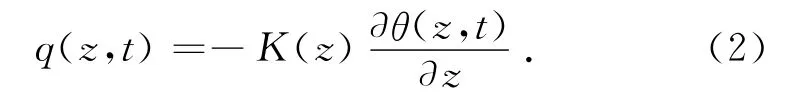
式中：∂θ（z，t）／∂z为轨道结构温度沿深度的变化率，即温度梯度；K（z）为轨道结构沿深度方向的材料的导热系数.

当热量进入或离开物体（或者一定质量的物质）时，物体的温度会发生变化，温度变化率与物体材质有关，并且存在如下关系［9］：

式中：∂q（z，t）／∂z为单位时间内通过其表面（等温面）的热通量，∂θ（z，t）／∂t为轨道结构温度变化率，ρ（z）为沿轨道结构深度方向的质量密度，c（z）为沿轨道结构深度方向的比热容.

把式（2）、（3）代入式（1），可得无砟轨道结构的一维热传导方程：

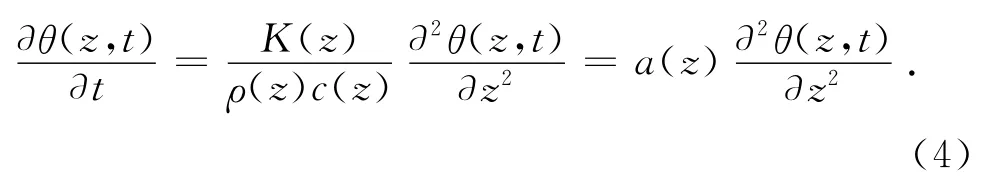
式中：a（z）为轨道结构材料的导温系数.

无砟轨道结构中的轨道板和支承层（底座）等构件都是混凝土材料，各种材料的导温系数较接近，有的轨道结构类型虽然设置了CA砂浆层，但一般的CA砂浆与水泥浆的热物理性质比较接近，导温系数与混凝土仅存在微小差异，且因层厚为3～5 m，可取与混凝土材料相同的导温系数，多层传热问题可简化为均质半无限空间一维传热问题.对各层材料的导温系数统一取a=a（z）=0.003 m2／h.

1.2 无砟轨道结构传热问题边界条件描述

固体传热问题的求解与其边界条件存在极大的关系.当已知轨道结构表面温度时为第一类边界条件；当已知轨道结构表面各点热量的流速时为第二类边界条件；当仅知轨道结构表面温度是周期函数时为第三类边界条件［8］.而影响轨道结构表面温度的主要因素包括空气温度、太阳辐射、风速及结构表面特性等［9～10］.

我国建筑热工设计规范［11］、英国标准［12］等都给出了有关混凝土结构物表面等效温度的计算公式：

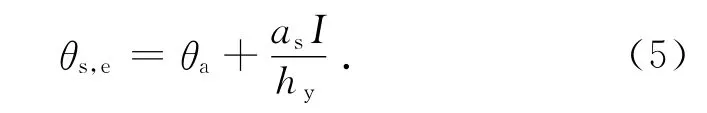
式中：θs，e为轨道结构表面等效温度；θa为轨道结构周围环境气温；I为轨道结构表面（水平面）太阳辐射照度（强度）；as为太阳辐射吸收系数.对水泥混凝土表面取as=0.4～0.7，对光滑的无砟轨道取as=0.4；hy为表面换热系数，hy=ar+acv，其中长波热辐射系数ar=4.15，对流换热系数acv按如下规定取值：当风速v≤5 m／s时，acv=6+4v，当风速v≥5 m／s时，acv=7.41v0.78［9-10］，本文采用日平均风速计算acv.

晴天太阳辐射在日出到日落时段内近似服从正弦或余弦曲线变化［13-14］，太阳辐射对轨道板表面产生的当量温度可用分段函数近似表示为

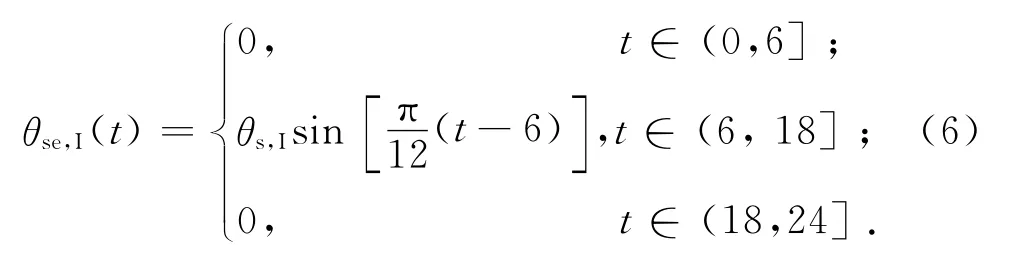
式中：θse，I（t）为太阳辐射在t时对轨道结构表面产生的当量温度；θs，I=asIdπ／（2hytd）为太阳辐射在轨道结构表面产生当量温度的最大值；Id为轨道结构表面（水平面）日太阳辐射照度（强度）；td为日照时间；t为时间，当t=6时为早上6时.

研究表明：气温变化近似服从正弦或余弦函数变化［10］，某时刻的气温可表示为如下形式：

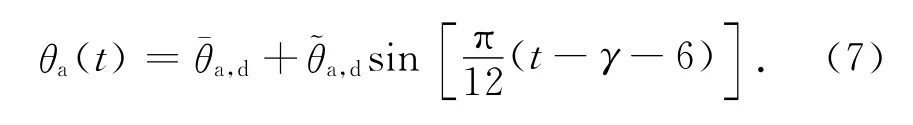
式中：θa（t）为某日t时的环境气温；¯θa，d与~θa，d分别为环境气温的日平均值和幅值；γ为最大太阳辐射时（正午12点）与最高气温出现时的差值加1，如一天的最高气温出现在14时，则γ=3.

轨道结构表面等效温度幅值在白天由太阳辐射和气温幅值相叠加，而在夜间仅为气温幅值.把式（6）、（7）代入式（5），以轨道结构表面等效温度最大的时刻为峰值点，并对板面温度分布区间进行修正，可得无砟轨道结构表面等效温度计算公式：

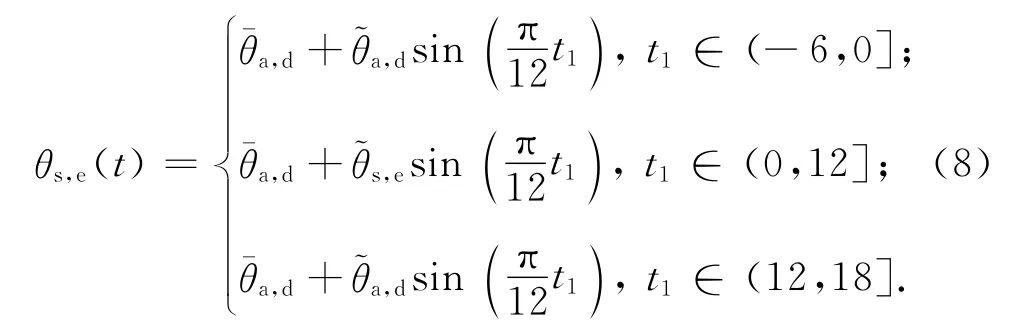
式中：θs，e（t）为轨道结构表面某日t时的等效温度；~θs，e为考虑太阳辐射作用引起的轨道结构表面在白天的等效温度幅值，t1=0为早上6+t0时，t0为因最大太阳辐射出现时与最高气温出现时的差值而引起轨道结构表面温度峰值变化的时间相位修正值，

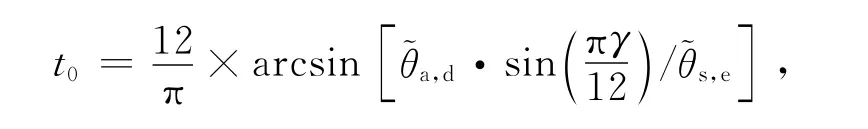
不同情况下的修正值计算结果如表1所示.

表1 BTS表面温度峰值时间相位修正值Tab.1 Corrected temporal phase for BTS surface peak tem-perature

1.3 无砟轨道结构温度场解析解

通过前述对轨道结构表面温度的数学描述和等效处理，无砟轨道结构热传导方程及边界条件可以表示为

式中：~θ为轨道结构表面等效温度幅值，白天取~θ=~θs，e，夜间取~θ=~θa，d，φ为相位角，φ=π（t-6-t0）／12.

无砟轨道结构温度场的解析解可以表示为

由于轨道结构的热阻作用及材料导热性能的差异，表面温度峰值进入轨道结构内部会产生延迟而引起温度波形的相位差.考虑温度分布的连续性，无砟轨道结构内部的温度场可以表示为

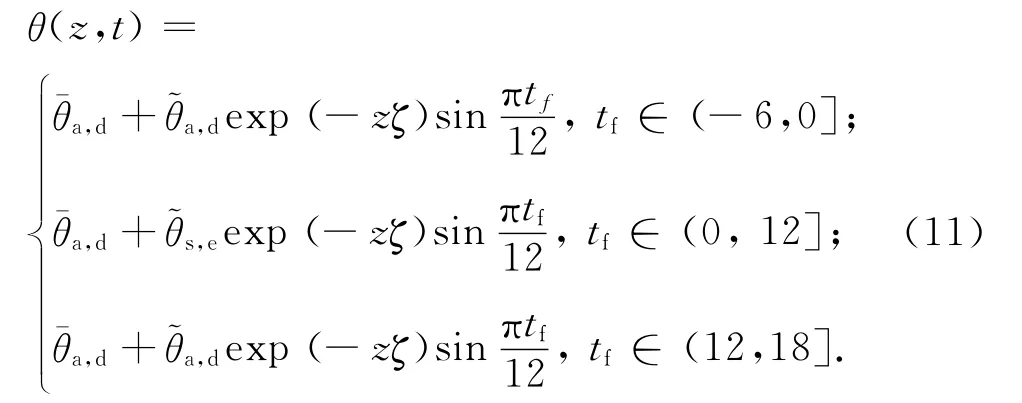
式中：tf=0为早上6+t0+12zζ／π时.

式（11）中tf与式（8）中t1的差异表示温度在轨道结构中传递的时间差.该差值与轨道结构不同层位的深度z有关，而温度数值随轨道结构深度增加而逐渐衰减，衰减速率为exp（-zζ），表明轨道结构内部温度呈非线性分布，不同层位构件的温度特性与所处位置有关.实际上，式（11）是基于固体传热学原理而得到的混凝土板温度场的解析解，对板式无砟轨道结构具有普适性，其差异主要来源于无砟轨道表面特性（太阳辐射吸收系数as）及结构层材料导温系数a等参数的取值，而这种参数取值所产生的差异十分有限，在工程应用中可以忽略不计.

2 实时温度场解析解验证

某高铁无砟轨道CRTS-II型板铺设时曾现场对轨道板的温度分布进行了跟踪实测，实测数据包括环境气温、轨道板表面温度和板底温度，实测时间为连续3 d，获得的温度数据比较有代表性，用其验证本文提出的实时温度场简化计算方法.当地气温和板面温度采用红外测温仪，轨道板板底温度用4个热电偶温度传感器埋设在轨道板的4个角点处进行测量.

根据当地城市的历史气象资料查询获取当天的气象数据，以此作为初始输入条件进行计算，并与实测的轨道结构温度数据进行对比，结果如图1和2所示.图中纵坐标θ（z=0，t）为式（11）中的温度场方程θ（z，t）在轨道结构深度z=0处t时的温度，下同.

图1 CRTS-II型轨道板表面温度实测值与计算值Fig.1 Measured and calculated temperature at CRTS-II track slab surface

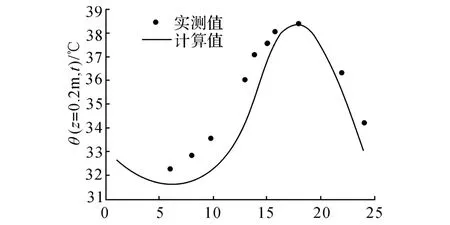
图2 CRTS-II轨道板板底温度实测值与计算值Fig.2 Measured and calculated temperature at CRTS-II track slab bottom

吴继臣等［7-16］在京沪高铁铺设CTRS-II型轨道板期间对轨道板温度进行现场实测，采用本文的计算方法进行计算，选取其中某一日晴天的温度实测数据进行对比，结果如图3、4所示.

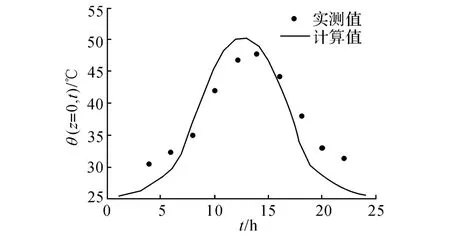
图3 轨道板表面温度的计算值与文献实测值Fig.3 Temperature of measured in literature and calculated in this study at track slab surface

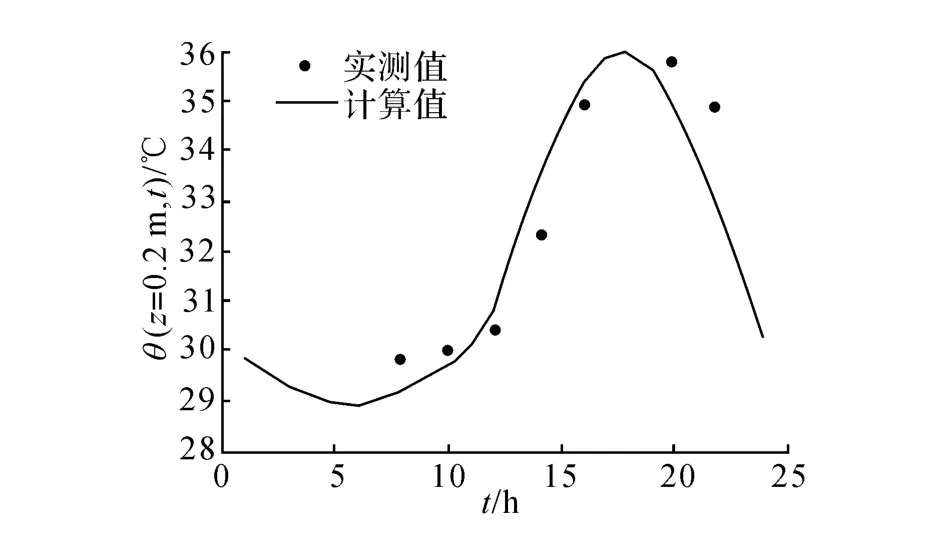
图4 轨道板底部温度的计算值与文献实测值Fig.4 Temperature of measured in literature and calculated in this study at track slab bottom

图1～4的比较结果表明：轨道结构表面温度计算值与实测值的大小及变化规律基本一致，而轨道板板底温度计算值与实测值有部分存在较小差异，但是其最大偏差仅约为3℃，且其变化规律相符性较好，完全能够满足工程应用的需要，这表明本文提出的用于计算轨道结构温度场的简化方法在一定程度上是准确和有效的.当然，本文用于验证的数据有限，在后续研究中可继续对计算方法的有效性和准确性进行进一步验证.

3 轨道结构温度场分析

3.1 不同时刻轨道结构温度分布规律

以前述某高铁无砟轨道现场实测所在地区为研究对象，采用当地气象数据资料作为输入参数计算当天不同时间点轨道结构内部温度场的分布规律，结果如图5所示.

由图5可以看出，当天不同时间轨道结构上部0～0.2 m内温度变化频繁，0.2～0.4 m内温度变化相对较弱，而大于0.4 m范围几乎没有变化；轨道结构上部0.2 m范围的最大正温度梯度出现在13：00～15：00时左右.

图5 某地区高速铁路BTS温度场一天不同时间分布图Fig.5 Temperature distribution for high-speed railway BTS in a area，at one day

3.2 不同季节轨道结构温度分布规律

以当地1、4、7、10月代表不同季节，取各月气象数据资料的均值进行计算，不同季节各时间段轨道结构的温度分布规律如图6～9所示.

图6～9结果表明：轨道结构内部温度场在不同季节的分布规律基本相同，不同季节温度分布影响深度的偏差不大，最大温度梯度出现的时间基本相同，但不同季节最大正温度梯度的数值存在明显的差异，其中7月代表的夏季温度梯度最大，4月、10月代表的春、秋季温度梯度相对夏季较小，而1月代表的冬季温度梯度在4个季节中最小.

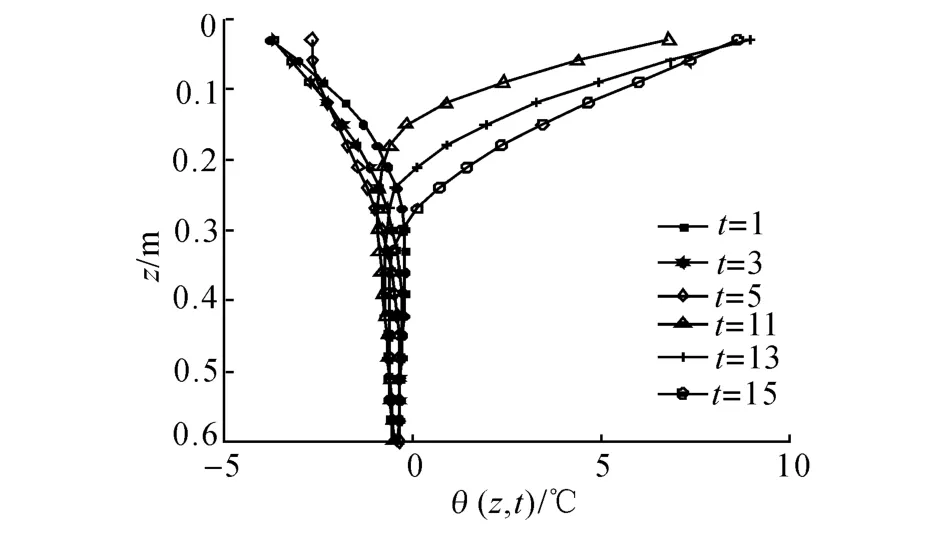
图6 某地区高速铁路BTS温度场1月份分布图Fig.6 Temperature distribution for high-speed railway BTS in a area，in January

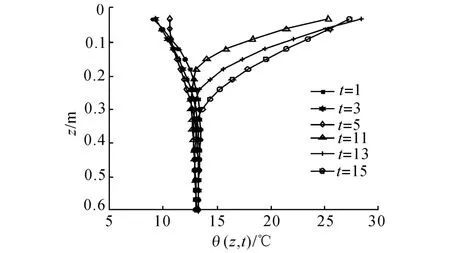
图7 某地区高速铁路BTS温度场4月份分布图Fig.7 Temperature distribution for high-speed railway BTS in a area，in April

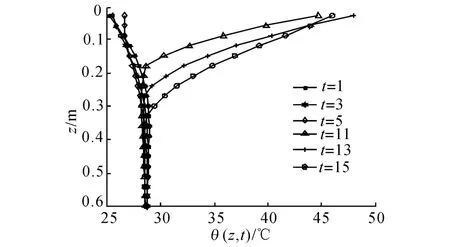
图8 某地区高速铁路BTS温度场7月份分布图Fig.8 Temperature distribution for high-speed railway BTS in a area，in July

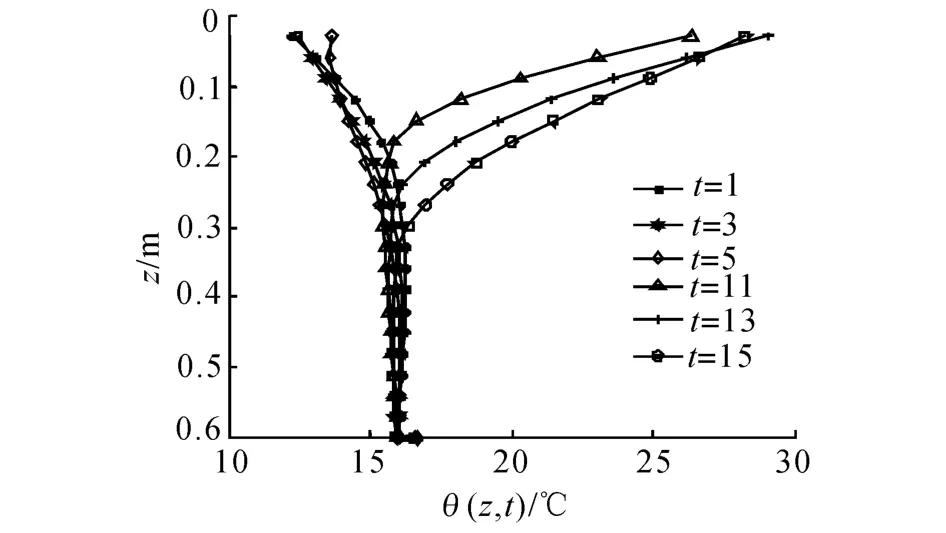
图9 某地区高速铁路BTS温度场10月份分布图Fig.9 Temperature distribution for high-speed railway BTS in a area，in October

实际上，无砟轨道结构不同层位构件承受的温度应力与其均匀温度作用、温度梯度作用等温度特性有关，且不同结构体系无砟轨道类型也存在较大差别，特别是纵连式无砟轨道结构的温度特性更显复杂.在另文中已对这个问题进行了专门研究，本文主要针对无砟轨道结构温度场的简化计算方法和变化规律进行研究.

4 结 论

（1）利用气象资料描述的轨道结构温度场边界条件可以近似为正弦（或余弦）分布的函数，并可以简化为热传导方程求解；

（2）高铁CRTS-II型轨道板现场实测的温度数据及本文的计算结果表明：本文提出用于计算轨道结构温度场的简化方法能够准确、有效地用于解决工程问题.

（3）计算结果表明：轨道结构温度分布在上部0～0.2 m内受外界环境温度影响变化明显，0.2～0.4 m内受外界环境温度影响变化相对较小，而0.4 m以下基本没有变化.

（4）轨道结构上部0～0.2 m内温度场最大正温度梯度出现在13：00～15：00，而不同季节中夏季的最大温度梯度最大，冬季最小.

（

）:

［1］LIU X，ZHAO P，DAI F.Advances in design theories of high-speed railway ballastless tracks［J］.Journal of Modern Transportation，2011，19（3）：154- 162.

［2］中华人民共和国铁道部.TB 10621-2009高速铁路设计规范（试行）［S］.北京：中国铁道出版社，2010：197- 225.

［3］卫军，班霞，董荣珍.温度作用对CRTS II型无砟轨道结构体系的影响及损伤分析［J］.武汉理工大学学报，2012，34（10）：80- 85.WEI Jun，BAN Xia，DONG Rong-zhen.Analysis of effects and damage of CRTS II ballastless track structure system induced by temperature［J］.Journal of Wuhan University of Technology，2012，34（10）：80- 86.

［4］徐庆元，范浩，李斌.无砟轨道温度梯度荷载对列车-路基上板式无砟轨道系统动力特性的影响［J］.铁道科学与工程学报，2013，10（3）：1- 6.XU Qing-yuan，FAN Hao，LI Bin.Influence of temperature gradient load of slab on dynamic characteristic of train-slab track on subgrade system ［J］.Journal of Railway Science and Engineering，2013，10（3）：1- 6.

［5］中华人民共和国国家标准.GB 50009-2012，建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012：64- 66.

［6］邵丕彦，李海燕，吴韶亮，等.CRTSⅠ 型轨道板温度变形及与砂浆垫层间离缝的测试研究［J］.中国铁道科学，2013，34（2）：18- 22.SHAO Pi-yan，LI Hai-yan，WU Shao-liang，et al.Measurement and research on temperature warping of CRTSⅠtrack slab and crack between track slab and cement asphalt mortar cushion ［J］.China Railway Science，2013，34（2）：18- 22.

［7］刘钰，赵国堂.CRTSⅡ型板式无砟轨道结构层间早期离缝研究［J］.中国铁道科学，2013，34（4）：1- 7.LIU Yu，ZHAO Guo-tang.Analysis of early gap between layers of CRTSⅡslab ballastless track structure［J］.China Railway Science，2013，34（4）：1- 7.

［8］胡汉平.热传导理论［M］.合肥：中国科学技术大学出版社，2010：12- 38.

［9］DURACRETE.Probabilistic performance based durability design of concrete structures：models for environmental actions on concrete structures［R］.Goteborg：The European Union-Brite EuRam III，1999.

［10］LARSSON O.Climate related thermal actions for reliable design of concrete structures［D］.Lund：Lund U-niversity，2012.

［11］中华人民共和国国家标准.GB 50176-93民用建筑热工设计规范 ［S］.北京：中国建筑工业出版社，1993：21- 42.

［12］BS-7527-2.6：1991，Classification of environmental conditions-environmental conditions appearing in nature ［S］.London：British Standards Institution，1991.

［13］吴继臣，徐刚.全国主要城市冬季太阳能辐射强度的研究 ［J］.哈 尔 滨 工 业 大 学 学 报，2003，35（10）：1236- 1239.WU Ji-chen，XU Gang.Major Chinese cities solar radiant intensities in winter［J］.Journal of Harbin Institute of Technology，2003，35（10）：1236- 1239.

［14］GUL M S，MUNEER T，KAMBEZIDIS H D.Models for obtaining solar radiation from other meteorological data［J］.Solar Energy，1998，64（1）：99- 108.

［15］WANG D，ROESLER J R，GUO D Z.Analytical approach to predicting temperature fields in multilayered pavement systems ［J］.Journal of Engineering Mechanics，2009，135（4）：334- 344.

［16］刘钰，陈攀，赵国堂.CRTSⅡ型板式无砟轨道结构早期温度场特征研究［J］.中国铁道科学，2014，35（1）：1- 6.LIU Yu，CHEN Pan，ZHAO Guo-tang.Analysis of early gap between layers of CRTSⅡslab ballastless track structure［J］.China Railway Science，2014，35（1）：1- 6.