基于在线SVM的裂解炉燃料气热值软测量

李奇安，郭 强

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺113001）

乙烯裂解炉燃料气系统是乙烯装置中的重要设备，用于连续、平稳地向裂解炉提供燃料气，保证裂解反应所需的高热量［1］.燃料气的热值是影响裂解炉炉管出口温度（coil outlet temperature，COT）的主要因素.燃料气系统中化学反应复杂、不确定干扰因素多，难以建立有效的热值机理模型［2］.而在线热值仪的测量结果存在明显的测量滞后［3］，不能有效地用于炉管出口平均温度的实时控制.采用过程数据建立这些难测变量的软测量模型是解决此问题的有效方法之一［4］.

早期的软测量建模技术是基于历史数据建立离线模型，主要方法包括人工神经网络（ANN）［5］、主元分析（principal component analysis，PCA）［6］及偏最小二乘（partial least squares，PLS）［7］等.早期的离线模型虽然能够较好地拟合历史数据，但是由于缺乏在线学习能力，早期的软测量建模技术存在2方面的问题：其一，模型的泛化能力严重依赖对初始建模样本的选择，如果所选的初始建模样本不能涵盖所有工况，则模型的泛化能力难以得到保证；其二，即使收集到足够多的历史数据，如何选择良好的模型类型及参数以保证模型能够适用于所有工况，同时尽量减少模型的复杂度，仍然是一个需要权衡的问题.因此，离线模型的性能在投用一段时间后会逐渐降低［8］.

大多数工业过程都具有慢时变特性，造成这种现象的主要原因包括输入物料的改变、催化剂活性失活及元器件磨损等，因此，工业过程需要一个具有自适应能力而不是固定不变的模型［9］.为此很多研究者提出了在线建模方法.何晓斌等10］提出了一种可变移动窗主元分析法（variable moving window principal component analysis，MWPCA）用于过程状态的自适应监控，该方法根据样本数据迭代更新相关函数矩阵，并结合移动窗技术（moving window technique）和R-特征值分解算法（rank-rsingular value decomposition，R-SVD）建立新的PCA模型.仿真结果显示MWPCA可以有效地用于慢时变过程的自适应监控.Li等［11-12］提出了迭代PCA／PLS算法用于过程的建模与监控，通过在PCA／PLS中引入迭代更新算式，使得模型可以根据新样本自适应更新模型.Wang等［13］提出了一种将PLS算法与Hammerstein神经网络相结合的PLS-based HRNN建模方法，其中PLS技术分解高维数据，Hammerstein神经网络拟合非线性动态过程函数，仿真结果显示该建模算法可以有效地用于铝酸盐产量的在线自适应预测.

目前，工业领域中应用较多的仍然是基于滑动窗口和迭代PCA／PLS的建模技术［14-16］，仍然存在滑动窗口尺寸难于选择、每样本数据更新所需计算量大、PCA算法不能反映建模所需的输入输出变量间的关系以及PLS算法不能建立非线性模型等问题.因此，工业过程还缺乏一套有效的非线性自适应在线建模算法.

增量式支持向量机［17］是支持向量机（support vector machine，SVM）［18］的在线自适应版本，该算法既保留了支持向量机的优点，同时又具有在线自适应能力，因此，在处理很多实际问题时表现出优良的性能［19-21］.

近似线性依靠（approximate linear dependence，ALD）条件可以有效地用于监控慢时变工业过程的漂移现象并减少每样本更新策略所带来的计算负荷，常作为模型的更新决策条件［22-23］.

乙烯裂解炉燃料气热值软测量模型目前主要采用离线建模法，刘漫丹等［2］将模糊逻辑系统、小脑关节控制器和神经网络结合，开发出了一种智能化的神经网络算法.仿真结果显示，该算法具有更好的平滑能力和泛化能力，基于该算法的热值软测量系统，长期应用在具有强烈干扰的现场环境下，显示出了良好的热值预测准确性.杨思远等［3］利用小波神经网络的降噪和非线性函数近似能力，提出了一种小波神经网络模型，用该模型对裂解炉燃料气热值进行测量，可以减少被“污染”的现场数据对模型预测精度的影响.张照娟［24］提出了一种具有递归环节的动态模糊神经网络，并运用改进的粒子群算法优化模糊神经网络的模型参数，最后利用这种方法“测量”燃料气热值，取得了较好的效果.

但是基于上述离线算法建立的模型缺乏自适应能力，随着工况的变化，模型在投用一段时间后会出现性能恶化甚至无法使用的现象.为此，本文运用Online SVM建模算法建立一个具有在线学习能力的热值软测量模型，该算法将增量式支持向量机（ISVM）与近似线性依靠（ALD）条件相结合，通过选择满足ALD条件的独立新样本更新SVM模型来保证算法的适时性.

1 Online SVM建模算法

Online SVM建模算法包括2部分：1）基于增量式支持向量机（ISVM）的非线性建模方法；2）基于近似线性依靠（ALD）的模型更新条件.

1.1 增量式支持向量机

增量式支持向量机最初由Cauwenberghs等［17］提出，它使传统的支持向量机具有在线增加或删除样本，同时不需要重新训练整个学习机器的能力.早期的ISVM只能处理分类问题，Ma等［20］将其推广，使其可以解决回归估计问题.

假设存在训练集T= ｛（xi，y i），i=1，…，l｝，其中xi∈Rn，n为输入空间维数，χi表示训练样本，y i∈R，y i表示模型的输出，l为样本总数.支持向量机算法的目标是在训练集T上寻找一个尽可能平滑的回归函数f（χ），在最大偏差ε内近似所有目标输出y i，f（χ）可以通过如下对偶最优化问题得到［17］.

式中：Qij=k（xi，xj）为核函数，i，j为样本标号，αi、α*i、αj及α*j为对偶系数，C是惩罚参数.ISVM 的目标就是在每个样本点上最小化式（1），而不用重新训练整个模型.式（1）属于凸最优化问题，其最优解应满 足 KTT（Karush-Kuhn-Tucker）条 件.设h（xi）=f（xi）-y i为边界函数，θi=αi-α*i为对偶系数差值，根据KTT条件，全体样本被分成支撑集S、误差集E和余集R［20］.

当获得新样本时，ISVM算法将重新分配上述集合中的样本点直到KTT条件重新满足.同理，当旧样本删除时，也按照此算法而不需要重新训练学习机器.

1.2 近似线性依靠

离线模型选择新样本点进行模型更新时，要考虑到这些样本的多样性和线性依靠性，只有选择那些独立新样本进行更新，才能保证模型的适时性.为此本文选用ALD条件来判断新样本可否用于模型更新，ALD更新条件如下［23］：

式中：xi（i=1，…，k）为训练样本，k为样本数；xk+1为新样本；ν为预先定义的正阈值；δk+1为新样本的近似误差值.更新算法的主要思想是通过计算新样本相对于建模样本的近似误差值δk+1，并比较其与阈值ν的关系，来判断是否采用新样本更新模型.当δk+1≤ν时，说明新样本与建模样本是线性依靠的，可以运用建模样本来线性表出，因此不需要进行模型更新；当δk+1＞ν时，新样本与建模样本是线性独立的，因此需要进行模型更新.

对于式（3）的求解，Tang等［23］给出了详细的推导步骤，当新样本点加入时，通过求解δk+1关于a的微分，可以得出新样本的近似误差值δk+1、新样本及建模样本间的关系式，表示如下：

式中：k k+1=xk+1·xTk+1为新样本归一化值，xk+1为新样本归一化向量，~Kk=Xk·XTk为建模样本矩阵，Xk为建模样本归一化向量，~kk=Xk·xTk+1为建模样本与新样本相关矩阵.

1.3 Online SVM算法

以下给出Online SVM算法的伪代码：

在ALD更新条件中，对阈值ν尚无系统的选择方法，通常由专家经验设定.较高的ν会减小机器的负担，但是会降低模型预测准确性；较低的阈值虽然能够提高模型预测准确性，但是也增加了计算消耗，因此，在建模前选择合适的ν非常重要.

2 裂解炉燃料气热值软测量建模

2.1 裂解炉燃料气热值的影响因素

在石油化工行业中，由于装置的化学反应复杂、干扰因素多等原因，传统的机理建模方法往往难以实现.软测量建模方法经过多年来的发展，其理论体系已日趋完善，在石化行业中已有很多成功的应用.如裂解炉出口乙烯和丙烯收率的软测量及催化裂化分馏塔粗汽油干点软测量等［25］.在建立软测量模型的过程中，建模对象的工艺分析过程非常重要.

以某厂燃料气系统为例，其简易工艺流程图如图1所示.稳态工况下，乙烯装置自产甲烷氢并入燃气储罐F1作为裂解炉燃料；动态工况下，乙烯装置自产甲烷氢减少，储罐F1的压力发生波动，为了保持储罐F1压力的稳定，液化石油气（LPG）燃料并入储罐F1补足.可见燃料气热值主要受燃料气组份流量和压力波动的影响.因此，在热值软测量建模时应选择燃料气流量，燃料气压力和LPG压力作为软测量模型的输入变量，而燃料气热值则为输出变量.

图1 燃料气系统工艺流程图Fig.1 Fuel gas system process chart

2.2 基于Online SVM的裂解炉燃料气热值软测量建模方法

根据裂解炉燃料气热值的影响因素，并结合Online SVM算法，提出裂解炉燃料气热值在线建模方法，该方法包括离线训练和在线模型更新2个模块，流程如图2所示.

热值 影 响 因 素 输 入 向 量 X= ｛（qv，p1，p2）i，i=1，…，k-1｝，热值输出向量Y=｛y i，i=1，…，k-1｝，其中qv、p1及p2分别为燃料气流量、燃料气压力和LPG压力，k为样本总数，y i为样本i下的燃料气热值.

2.2.1 离线训练模块 离线训练模块的功能是基于离线数据训练得到初始热值软测量模型.将燃料气流量、燃料气压力和LPG压力作为输入变量，燃料气的热值作为输出变量送入SVM回归机中进行学习，得到热值模型的结构如下：

式中：b为偏置项.在初始训练中，离线数据集的选择应该尽量覆盖所有工况，这样可以减少新样本的加入，进而减少模型的更新次数.

2.2.2 在线更新模块 在线更新模块的功能是使离线模型学习有价值的新样本，保证热值模型在新的工况下仍能准确预测热值.现场装置采集到的新样本首先需要经过ALD条件判断，以保证所选择的新样本相对于建模样本是近似线性独立的，然后运行ISVM算法对新样本进行学习，得到新模型后替换离线模型.

图2 基于Online SVM的裂解炉热值软测量流程图Fig.2 Soft sensor procedure of calorific value based Online SVM

3 仿真实验

仿真实验中使用合成数据、Benchmark数据和燃料气热值数据对Online SVM建模算法进行仿真研究.首先运用合成数据和Benchmark数据验证该算法的有效性，然后将其用于燃料气热值实验，以检验算法的自适应性.在仿真实验中，将SVM［17］和LS-SVM［27］算法与本文算法进行对比研究.采用均方根误差（RMSE）和平均绝对误差（MAE）作为评价建模精度的准则.将RMSE和MAE定义如下：

式中：y i、ˆy i分别表示燃料气热值的真实值和预测值，l为样本总数.

3.1 合成数据仿真

合成数据仿真由Tang等［23］中的非线性函数产生：

式中：z为合成数据输入，z∈ ［-1，1］；Δisy为噪声，Δisy∈［-0.1，0.1］；χjsy为非线性函数输入；F为非线性函数输出；isy=1，2，…，6，jsy=1，2，…，5.

图3 合成数据在线预测图Fig.3 Prediction results of testing samples for synthetic data

表2 合成数据测试结果Tab.2 Testing result for synthetic data_______

从第90个样本点开始，过程处于突变工况.从图3中可以看出，此时SVM和LS-SVM算法无法适应这种突变，不能准确地预测输出，而Online SVM建模算法依靠在线学习能力，能适应工况的改变并准确预测输出的变化.图4为测试样本ALD值与阈值的对比图，图4中σ=log（δk+1）为ALD值.从图中可以看出，超过阈值的样本主要集中在后半段，对应于过程的突变工况.

图4 合成数据ALD值图Fig.4 ALD value on synthetic data

运用3个经典的合成数据集：Friedman 1、2和3［26］来测试提出算法的预测性能.每个数据集共有100个样本，分别将标准差为0.1的高斯噪声加入其中.随机选择60个样本用于训练，40个样本用于预测.测试结果如表3所示.表3中，tcpu为执行时间，UN为样本更新数目.测试结果表明：1）LSSVM与Online SVM、SVM相比，具有较快的运算速度，这主要是由于LS-SVM算法引入了误差范数，使得不等式二次规划求解问题转化为二次规划求解问题，大大降低了计算复杂度，但是也使得所有的样本都变成了支持向量［27］；2）Online SVM 具有在线学习能力，因此，与SVM、LS-SVM相比，具有较好的预测准确性.

表3 Friedman数据集测试结果Tab.3 Testing results for Friedman data Friedman

3.2 Benchmark数据仿真

Benchmark数据集来源于现实事件，主要用于测试机器学习算法的性能.这里选用波士顿房价（Boston housing）和计算机性能（Comp-active）数据集进行仿真验证［22］.波士顿房价数据集包括13个输入变量和1个输出变量，共计506个样本点.数据集根据户口普查数据预测波士顿各地区房价均值.计算机性能数据集包括12个输入变量和1个输出变量，共计6 192个数据点.数据集根据系统活动状态预测电脑的CPU利用率.仿照Friedman仿真实验，随机选择56个波士顿房价样本和50个计算机性能样本测试模型的泛化能力，测试结果如表4所示.从表4中数据可以看出：1）Online SVM预测准确性最高，学习现实世界问题的能力强；2）随着样本数量的增加，Online SVM需要的运算时间变长，这主要是由于大样本非线性规划问题的求解过程计算消耗大，如果样本量适度，则可以忽略计算消耗问题.

3.3 燃料气热值建模仿真

根据某厂裂解炉燃料气系统现场采集的数据，运用Online SVM建模算法进行建模预测.为了模拟工业现场的时变性，将采集的130个样本，分成C1、C2和C3.其中C1包括50个样本，C2包括50个样本，C3包括30个样本.随机选择C1和C2中的各40个样本组成训练集，剩余的样本和C3组成测试集.对于离线训练模型来说，相对于C1和C2，C3属于突变工况.训练数据和测试数据的分组情况如图5所示，其中y为燃料气热值.

图5 训练数据和测试数据分组示意图Fig.5 Train sets and test sets schematic diagram of packet

热值实验的仿真结果如图6所示，表5为热值实验的详细测试结果.从表5和图6中可以看出，具有在线学习能力的Online SVM算法即使处于突变情况仍能很好地预测热值.

图7为模型在线学习过程中，新样本ALD值与阈值的对比图.从图7中可看出，超过阈值的样本同样集中在后半段.由于在ALD更新条件中，阈值v的选择对建模预测精度和建模速度都有非常大的影响，表6给出了阈值v不同时，模型性能的变化情况.表6表明：随着阈值v的增大，参与更新的样本点减少、模型的预测精度下降，训练时间大大减少.如表6中最后一列所示，当v=ln（-30.5）时，虽然训练时间缩短为0.7 s，但同时RMSE和MAE增加到了17.76和11.97.

表4 Benchmark数据集测试结果Tab.4 Testing result for Benchmark data

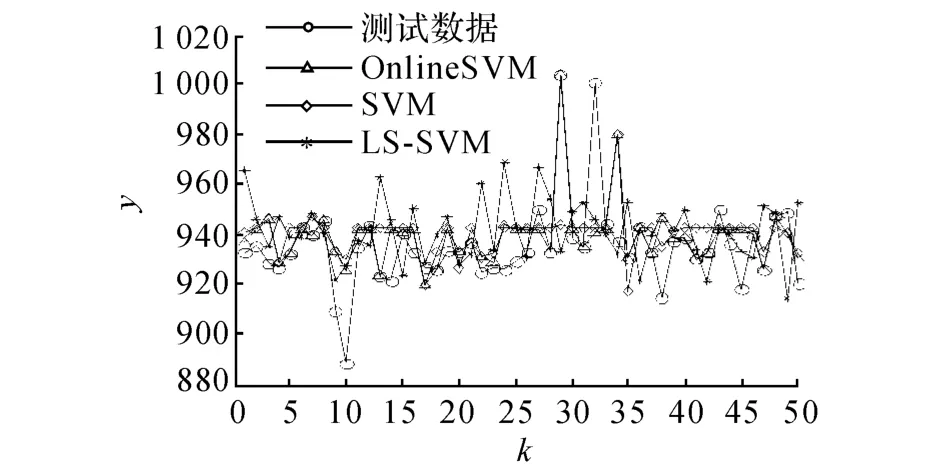
图6 燃料气热值在线预测图Fig.6 Prediction results of testing samples for calorific value

表5 燃料气热值测试结果Tab.5 Testing result for calorific value

图7 热值数据ALD值图Fig.7 ALD value of calorific value data

表6 不同阈值下热值模型性能测试结果Tab.6 Performance comparison for calorific value model under different threshold

4 结 语

基于Online SVM的热值软测量建模算法，能够用于燃料气热值的在线预测，预测模型的性能可以满足工业现场的应用要求.建模过程中通过判断新样本的ALD值，不但能够检测出过程的突变情况，同时又能避免样本更新所带来的计算负荷，提高了模型的学习效率.ALD条件中阈值v的选择对模型的性能存在较大影响，使用者应该根据实际情况选择合理的值.

本文算法经过一定的修改，还可以用于其他的软测量建模领域.下一阶段研究工作的重点将围绕如何优化Online SVM的求解过程以缩短计算时间，以及如何更新模型参数和模型样本以减少对模型预测精度的影响展开.

（

）:

［1］刘崇明.乙烯装置燃料气系统设计缺陷及改进［J］.乙烯工业，2001，13（4）：33- 37.LIU Chong-ming.Ethylene plant fuel gas system design defects and improvement［J］.Ethylene Industry，2001，13（4）：33- 37.

［2］刘漫丹，杜文莉，钱锋.裂解炉燃料气热值的模糊神经网络软测量［J］.计算机集成制造系统-CIMS，2003，9（5）：412- 416.LIU Man-dan，DU Wen-li，QIAN Feng.Soft sensing system of fuzzy-neural network for cracking fuel gas enthalpy［J］.Computer Integrated Manufacturing System，2003，9（5）：412- 416.

［3］杨思远，徐佩亮，王振雷.基于小波神经网络的热值软测量建模［J］.石油化工自动化，2011，47（4）：34- 37.YANG Si-yuan，XU Pei-liang，WANG Zhen-lei.Modeling of soft measurement for calorific values based on wavelet neural network［J］.Automation in Petro-Chemical Industry，2011，47（4）：34- 37.

［4］THAM M T，MONTAGUE G A，MORRIS A J.A soft-sensors for process estimation and inferential control［J］.Journal of Process Control，1991，1（1）：3- 14.

［5］YANG Y X，CHAI T Y.Soft sensing based on artificial neural network［C］∥ Proceedings of the 1997 American Control Conference.America：［s.n.］，1997，1：674- 678.

［6］ROTEM Y，WACHS A，LEWIN D R.Ethylene compressor monitoring using model-based pca［J］.American Institute of Chemical Engineers Journal，2000，46（9）：3- 14.

［7］ZHANG H W，LENNOX B.Integrated condition monitoring and control of fedbatch fermentation processes［J］.Journal of Process Control，2004，14（1）：41- 50.

［8］KADLEC P，GRBIC R，GABRYS B.Review of adaptation mechanisms for data-driven soft sensor［J］.Computers and Chemical Engineering，2011，35（1）：1- 24.

［9］WANG X，KRUGER U，LENNOX B.Recursive partial least squares algorithms for monitoring complex industrial processes ［J］.Control Engineering Practice，2003，11（6）：613- 632.

［10］HE X B，YANG Y P.Variable mwpca for adaptive process monitoring［J］.Industrial and Engineering Chemistry Research，2008，47（2）：419- 427.

［11］LI W H，YUE H H，VALLE C S.Recursive pca for adaptive process monitoring ［J］.Journal of Process Control，2000，10（5）：471- 486.

［12］QIN S J.Recursive pls algorithms for adaptive data modeling［J］.Computers and Chemical Engineering，1998，22（4）：503- 514.

［13］WANG W，CHAI T Y，YU W.Modeling component concentrations of sodium aluminate solution via hammerstein recurrent neural networks［J］.IEEE Transactions on Control System Technology，2012，20（4）：971- 982.

［14］WANG X，KRUGER U，IRWIN G W.Process monitoring approach using fast moving window pca［J］.Industrial and Engineering Chemistry Research，2003，11（6）：613- 632.

［15］CHOI S W，MARTIN E B，MORRIS A J.Adaptive multivariate statistical process control for monitoring time-varying processes［J］.Industrial and Engineering Chemistry Research，2006，45（9）：3108- 3118.

［16］FAISAL A，SALMAN N，YEONG K Y.A recursive plsbased soft sensor for prediction of the melt index during grade change operations in HDPE plant［J］.Korean Journal of Chemical Engineering，2006，26（1）：14- 20.

［17］CAUWENBERGHS G，POGGIO T.Incremental and decremental support vector machine learning［C］∥ Proceedings of the 2001 in Advances in Neural Information Processing Systems.Spain：NIPS，2001，13：409- 415.

［18］VLADIMIR N V.Statistical learning theory［M］.New York：Wiley，1998.

［19］LASKOV P，GEHL C，KR UGER S.Incremental support vector learning：analysis，implementation and applications［J］.Journal Machine Learning Research，2006，7（1）：1909- 1936.

［20］MA J S，THEILER J，PERKINS S.Accurate on-line support vector regression［J］.Neural Compute，2003，15（11）：2683- 2703.

［21］GIOVANNI M，FRANCESCO P.Learning to trade with incremental support vector regression experts［C］∥ HAIS'08 Proceedings of the 3rd International Workshop on Hybrid Artificial Intelligence Systems.Spain：HAIS，2008，5271：591- 598.

［22］ENGEL Y，MANNOR S，MEIR R.The kernel recursive least squares algorithm［J］.IEEE Transactions on Signal Processing，2004，52（8）：2275- 2285.

［23］TANG J，YU W，CHAI T Y.On-line principal component analysis with application to process modeling［J］.Neuro Computing，2012，82（1）：167- 178.

［24］张照娟.动态模糊神经网络的研究及在燃料气热值软测量中的应用［D］.上海：华东理工大学，2008.ZHANG Zhao-juan.Research on dynamic fuzzy neural network and its application to soft sensing for calorific value［D］.Shanghai：East China University of Science and Technology，2008.

［25］孙优贤，褚健.工业过程控制技术（方法篇）［M］.北京：化学工业出版社，2005：376- 383.

［26］JEROME H F.Multivariate adaptive regression splines［J］.The Annals of Statistics，1991，19（1）：1- 67.

［27］SUYKENS J A K，BRABANTER J D，LUKAS L.Weighted least squares support vector machines：robustness and sparse approximation［J］.Neurocomputing，2002，48（1）：85- 105.