基于时频相关性的复合常规人为干扰分析方法*
张敬义,李永贵
(1.解放军理工大学 通信工程学院 研究生1 队,南京210007;2.南京电讯技术研究所,南京210007)
1 引 言
干扰信号可分为自然干扰和人为干扰,人为干扰又可分为无意干扰和蓄意干扰,而人为干扰,特别是蓄意干扰,是军事无线通信系统面临的最大和最直接的威胁。无论是数字通信还是模拟通信,若要达到对通信接收端的高效干扰,至少要在时间和频域对其进行有效覆盖。从通信接收端受干扰的频点来看,人为干扰的中心频率变化主要有以下几种形式:一是干扰的频谱在一段时间内保持不变或周期性变化,如定频干扰(单音、多音、部分频带干扰等),以及周期性的脉冲干扰;二是随时间在频域上作线性或非线性变化的周期性扫描,如线性或非线性扫频干扰;三是以上几种类型的复合。基于人为干扰的上述特征,寻找一种可行方法能够在特定域对复合人为干扰进行特征分析和参数提取,在满足算法的实时性和参数提取准确性情况下,为通信系统的综合抗干扰决策提供实时信息支持,对于提高智能抗干扰水平具有重要意义。
由于无意人为干扰和自然干扰并不针对任何特定目标,其出现具有随机性,故本文中将无意人为干扰和自然干扰统称为随机干扰,并对随机干扰影响下的蓄意人为干扰进行分析、识别和干扰特征参数的提取。由于随机干扰通常是时变的、非平稳的,且蓄意人为干扰的干扰策略对于通信方而言也是时变的、不确定的,因此,随机干扰影响下的蓄意人为干扰通常是复合的多分量信号。在多分量信号参数提取方面,国内外已有很多相关的研究。文献[1]中,作者指出多分量信号需满足各分量在某个域是分离的,该信号才是可分离的。在此基础上,陆续发展出了各种多分量信号分离的算法,如经验模态分解法[2]、信号分量多项式拟合法[3]、时频分析法[4]、独立分量分析方法[5]等。然而,以上方法的前提条件都是多分量信号在某个域具有可分离性,否则就很难分离。
对于随机干扰影响下的复合蓄意干扰信号,可能在时域、时频域或其他域存在相关或交叉的分量,考虑通过短时傅里叶变换(Short- time Fourier Transform,STFT)算法对复合干扰信号在时域和频域的关系进行分析和处理,并尝试使用分类搜索算法将复合的蓄意人为干扰解析成能够识别的基本干扰类型,对于不能解析和识别的干扰分量,用统计的方法对干扰频点的时间占用度进行分析。理论分析和仿真结果表明,通过分类搜索算法能够较好地提取复合人为干扰的特征参数。
2 算法的总体思路
对通信收发双方而言,通信信号的调制方式及对应的调制波形通常是先验已知的,且每种调制信号相关的抗干扰门限也是可以计算得到的。由于篇幅所限,本文不考虑通信信号的影响,仅对通信系统的干扰分量作独立地分析、识别和干扰参数的提取。
如图1所示,围绕“如何对随机干扰影响下的复合蓄意人为干扰进行分析、识别和参数的有效提取”这个问题,全文分以下三个部分来讨论:干扰信号模型的建立、干扰数据的预处理、基于分类搜索算法的人为干扰参数提取。

图1 系统模型Fig.1 The system model
干扰信号模型的建立是在Matlab 仿真环境中,通过将几种常规的人为干扰,如定频多音干扰、周期脉冲干扰、非线性扫频干扰等,以一定的方式组合起来(如干扰之间的交叉),最后,将随机干扰加载到人为干扰中;而随机干扰通过一定的干扰概率、干扰分布和干扰时间占用度等来控制。
干扰信号提取前先进行干扰数据的预处理,考虑使用STFT 对干扰信号进行时频变换,并对三维时频数据进行功率的判决,确定存在干扰的时频点,并得到二维的时频矩阵。由于STFT 算法不能兼顾时间和频率的分辨率,文中结合通信频点窄带带宽来确定STFT 算法的时频分辨率。
在时频矩阵的基础上,提出了分类搜索算法,根据干扰信号的特征参数,按照“定频解析、周期脉冲干扰解析、扫频干扰解析”的顺序对复合人为干扰进行自适应地解析。
3 复合干扰信号建模
假定复合干扰信号由“扫频干扰+定频干扰+周期脉冲干扰+随机干扰”组成,通过控制各个基本干扰的参数来构造不同复杂度的干扰模型,如各干扰模型之间互相交叉以及随机干扰不同程度地覆盖或者影响人为干扰特征。
(1)扫频干扰
采用二次型非线性扫频,并使用向上扫频fi(t)Hsaopin和向下扫频fi(t)Lsaopin两种形式,单位周期Tsaopin的扫频范围是[Fl,Fh],则在第i 个扫频周期内,干扰频率可表示为
(2)定频干扰
采用单音或多音干扰的形式,其时域表达式为

式中,fn(n=1,2,3,…,N)为可能的定频干扰频点。
(3)周期脉冲干扰
脉冲干扰的时域表达式如下:

式中,Dτ是宽度为τ 的矩形脉冲,A 为脉冲幅值,Tpulse为脉冲周期,k 为脉冲数。
(4)随机干扰
本文中将非蓄意的人为干扰和自然因素的影响统称为随机干扰。容易知道,此处的随机干扰在概率分布上可能是非高斯、非线性的,所以,随机干扰的模型并不能简单地用白噪声来构建。考虑到对复合人为干扰的解析是在时频域上,从而可通过随机干扰的时间占用度和频率占用度两个参数来控制和构建随机干扰分量。假设通信频点范围是[fa,fb],干扰信号观测时间为[tn,tm],被干扰的频点为fj(fa≤fj≤fb),频点总的干扰概率为ρf,则总的受扰频点数Njam=ρf·(fb-fa)/Δf(Δf 为时频分析的频率分辨率);干扰频点上的时间占用度为ρt,则每个受扰频点总的干扰时间为T(fj)=ρt·(tm-tn),且假设干扰时间T(fj)在[tn,tm]上服从均匀分布。
4 干扰信号的时频处理
4.1 时域到“功率-频率-时间”的时频域变换
假设复合人为干扰信号时域表示为y,采用矩形窗h(t),其短时傅里叶变换的表达式如下:
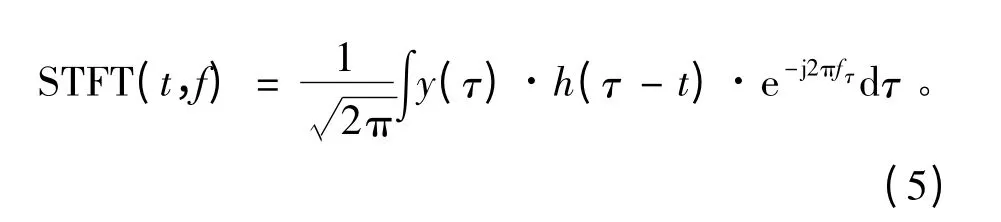
复合人为干扰y 是由各个基本干扰分量构成的,通过改变各个干扰分量的参数、交叉程度以及干扰功率来控制复合干扰的复杂度。
短时傅里叶变换最重要的是如何确定时间窗h的滑动长度和对应的时频分辨率。假设以通信频点fi为中心对应的窄带带宽为B,如图2所示,在窄带带宽B 内,可能有多个干扰频点,定义干扰有效的判决准则如下:

即在第i 个通信频带Bi内,若干扰功率Power_jami大于0,则通信频点fi所在的带宽Bi判决为有干扰,否则为无干扰。

图2 通信带宽B 内干扰频点分布情况Fig.2 The distribution of jamming in communication band B
在图2(a)中,两个干扰频点在Bi的边缘,可能会出现相邻带宽的重复判决或者无效判决的情形,为了提高干扰判决的准确率,应使得干扰数据的频率分辨率小于B/2,这里取为B/3。从而,在一个通信带宽内若存在两个以上的干扰时,能够保证干扰频点不全在通信带宽的边缘上,这样更有利于干扰的判决,如图2(b)所示。
若采样频率为fs,假设要达到的频率分辨率为Δf=B/3 + B/10,其中B/10 为频率分辨率保护间隔,使得一个窄带带宽B 内有不超过3 个干扰频点。若一次快速傅里叶变换(Fast Fourier Transform,FFT)的时间窗长度为T_window,则Δf 满足

从而,根据窄带带宽B 和采样率fs,并结合式(7),可以求出时间窗T_window。
4.2 干扰时频矩阵的计算
文中采用门限判决法,将“功率-频率-时间”的三维数据转化到“频率-时间”的二维数据,其过程实质上是在每个观测时刻和对应频率区间内,取小于或等于最大峰值的一个常数值λ 作为门限,对干扰的功率值进行二值化处理,其过程表示如下:

时频干扰矩阵获得的准确度和有效性与判决门限有关,判决门限越大,判决后保存原有信息量更大,但引入的随机干扰因素变大,影响干扰分量的提取;而判决门限越小,判决后损失的干扰分量信息变大,不利于较准确地提取干扰参数。在文献[6]中,作者取不同的判决门限值,并将估计值与理论值比较,选择使均方误差最小的门限值,通过仿真验证,得到合适的λ 取值,即λ=0.7·max(|STFT(t,f)|2)。
5 时频矩阵的单值化处理
本文中的处理对象为复合人为干扰信号,在随机干扰的影响下,其对应的时频矩阵在同一观测时刻t 上可能有多个干扰时频点,因此难以通过常规的线性或非线性拟合提取扫频干扰的参数。
假设每个通信信道带宽Bi=100 Hz,采样率fs=10 000 Hz,采用非线性扫频,扫频范围是[Fl,Fh]=[1500,3500]Hz,Tl-h=1 s;采用矩形时间滑动窗,窗口大小为T_window=228,且Δf =(fs/2)/(T_window/2 +1)=43.478 3 Hz,时间分辨率ΔT=(T_window/2)/fs=0.011 5 s。在一个通信带宽B 内若存在干扰频点,根据频率分辨率可知,频点可能会出现在如图2(c)所示的Jam1、Jam2、Jam3位置,对应的干扰功率为Power_Jam1、Power_Jam2、Power_Jam3;而若要判断该通信频点是否被干扰只需一个干扰频点存在即可,且一个带宽内多余的干扰频点会影响到干扰趋势的提取。因此,在不影响时间分辨率的基础上需要对一个B 内的多个干扰频点进行单值化处理。
针对这一问题,提出了单值化处理方法,即对一个通信带宽B 内干扰的分布进行判断,如Power_Jam1=0、Power_Jam2>0 且Power_Jam3>0 时,判定通信带宽B 内的干扰点为Jam3,同时删去Jam2。最终,根据处理后的时频二维数据不难看出,经过单值化处理,每个观测时刻对应的通信带宽B 内有不超过一个干扰频点,这对于下一步有效提取扫频干扰趋势具有重要意义。
需要注意的是,所提出的单值化处理方法,实质上是对通信带宽B 内的多个干扰频点进行合理地取舍,取舍的方法不同,单值化处理后的效果也不同。本文结合通信带宽B 来确定时频分辨率,使得每个B 内有不超过3 个干扰频点,则单值化处理的过程实质上是对3 个干扰频点(存在频点为1,不存在为0)取不超过一个频点,最终,使得相邻的通信带宽B 内的干扰频点整体保留原有的干扰趋势,且每个B 内有不超过一个的干扰频点。
6 分类搜索算法
假设通过门限判决得到的人为干扰的时频矩阵为A (t,f)M×N,对应的时间和频率的矩阵表示为t1×M和f1×N。
6.1 定频干扰的解析
从时域来看,定频干扰具有较大的时间占用度。因此,通过对干扰频点时间占用度进行逐频点搜索,将超过一定时间占用度门限的干扰解析为定频干扰。由于随机干扰及人为干扰相互间的影响,可能会造成观测时间内定频干扰的时间占用度小于100%,文中由仿真设定定频干扰占用度判决门限为T0=0.95。解析的算法具体如下:
For j=1:N
if [length(A(:,j)=1)/M]>T0=0.95
(1)记录定频干扰频点j;
(2)从时频矩阵A 中去除解析的定频干扰频点;
(3)干扰解析库的更新;
End
End。
6.2 周期脉冲干扰的解析
周期脉冲干扰解析的基本思想是,从脉冲干扰的周期性出发,对每个频点在观测时间上进行周期搜索,并对周期范围或者时间占用度进行约束,排除随机干扰造成的伪周期脉冲干扰。具体的算法如下:
For j=1:N
if ta<[length(A(:,j)=1)/M]<tb(对干扰频点时间占用度进行约束)
(1)temp=find(A(:,j)>0),即将满足占用度频点的非零点集中储存;
(2)T_temp=diff(temp),对非零点进行差分处理;
(3)if T_temp=常数>0(差分处理后各点相等,说明是一定周期的脉冲干扰);
(4)记录周期脉冲干扰频点和对应周期;
(5)删除解析的周期脉冲干扰对应频点值;
(6)干扰解析库的更新;
End
End
End。
6.3 扫频干扰的解析
如前所述,通过对时频矩阵进行单值化处理,同一时刻在每个通信信道带宽B 内有不超过一个(可能为0)的干扰频点,因此通过二叉树结构就能够表征不同时刻干扰在频域的分布情况。
扫频干扰解析的基本思想是,在一定的观测时间内,由于随机干扰不存在路径趋势,若始终存在连续的扫频趋势,且通过求取连续时间序列上基于二叉树结构的欧式距离和,并选取最小距离对应的路径作为扫频干扰路径,便能够在复合干扰中对扫频干扰进行解析。
在基于二叉树结构进行路径搜索时,首先要确定二叉树的“根”,即扫频干扰的起始频点。本文根据扫频干扰的特征来确定起始频点,即将时频矩阵中具有“连续几个相邻时刻对应频点同方向渐变”特征的点作为扫频干扰的起始点。
综合来看,扫频干扰搜索算法可表述如下:
(1)预处理:将经过定频和周期脉冲干扰解析后的时频矩阵先进行“插值处理”:当左右相邻时刻均满足扫频趋势,而该时刻或连续几个时刻一个带宽范围内无频点时,进行插值处理,具体插值可先在解析库中寻找,然后根据相邻时刻已知频点进行插值;
(2)搜索步骤:
For j=1:N
1)二叉树起始点的确定;
2)基于二叉树结构的最小欧式距离搜索;
3)扫频干扰解析点的记录和更新;
4)解析干扰库的更新;
5)时频干扰矩阵的更新;
6)j=j+2;
End。
6.4 随机干扰的解析
干扰时频矩阵通过“定频干扰搜索、周期脉冲干扰搜索、扫频干扰搜索”后,将其余不能够解析的干扰看作是随机干扰处理,算法表述如下:
For j=1:N
(1)length(find(A(:,j)>0))/M;即随机干扰时间占用度的计算;
(2)解析干扰库的更新;
(3)时频干扰矩阵的更新;
End。
6.5 交叉干扰时的处理
采用“搜索、记录、删除”的方法对复合人为干扰进行分类搜索,具体来说,先对某类干扰进行搜索,并在定义的干扰库中对其进行记录,同时从干扰时频矩阵中去除已搜索到的干扰。然而,若两种人为干扰在某一频点上有交叉,则前一种干扰解析和删除后,交叉频点的去除会对下一类型干扰的搜索和解析造成影响。
交叉干扰的判断和处理算法如下:
(1)定义已解析的干扰为定频干扰,待解析的干扰为扫频干扰,两种干扰存在两个交叉频点Fa(i,j)和Fb(i+1,j);
(2)若Fa(i,j)·Fb(i+1,j)>0,且

则Fa(i,j)和Fb(i +1,j)在定频干扰解析后不对其删除;
(3)对其他的干扰频点交叉类型,如一点交叉、三点交叉等,其处理方式与两点交叉相似,均是通过判断有无交叉点,以及交叉点左右邻近时刻的干扰趋势来作具体处理。
7 仿真与分析
涉及到的仿真参数主要有,采样频率fs=10 000 Hz,通信频点所在的窄带带宽B=100 Hz,采用矩形时间滑动窗且窗口T_window =228 点,作STFT 的频率分辨率为Δf =43.478 3 Hz,时间分辨率ΔT=0.011 5 s。仿真时间为4 s。干扰模型中,定频频率为,f1=3200 Hz,f2=4600 Hz;扫频干扰周期为2 s,扫频频率范围是1500~3500 Hz,其中在扫频周期内0~1 s为向上非线性扫频,1~2 s为向下非线性扫频;周期脉冲干扰的周期为0.1 s,采用占空比为1/10 的矩形实现,周期脉冲干扰载波为500 Hz;随机干扰采用频率干扰概率ρf和干扰频率的时间占用度ρt来控制,加载的随机干扰频率占用度为0.15,时间占用度为0.05,干扰频点和在时间和频率上服从均匀分布。
7.1 复合人为干扰模型的建立
如图3所示,对复合人为干扰信号进行短时傅里叶变换,得到“功率-频率-时间”的三维图,其中,定频f1=3200 Hz与扫频干扰有交叉频点,且在交叉点处功率值增大。图4是通过对三维时频图中的“功率”值进行门限判决后得到的“频率-时间”二维投影图,容易看到,在f2=4600 Hz周围有一些多余的频点,这主要是由于STFT 变换的时频分辨率不能兼顾造成的,这对于后期干扰特征参数的提取可能会造成误差。图5是对人为干扰加载随机干扰后进行的二维投影,其中,在1500 Hz、2500 Hz、4000 Hz等频点处随机干扰的时间占用度较大。

图3 人为干扰时域图Fig.3 The jamming in time domain

图4 人为干扰时频二维投影图Fig.4 The 2D shadow in time-frequency domain

图5 随机干扰影响下的人为干扰时频二维投影图Fig.5 The 2D shadow in time-frequency domain with random disturbance
7.2 定频干扰和周期脉冲干扰的解析
图6是解析得到的定频干扰和周期脉冲干扰,可以看出,通过时间占用度判决和周期的逐频点搜索,基本能够对定频和周期脉冲干扰进行较好地解析。而在516 Hz 处的周期脉冲干扰并没有被解析,这是由于随机干扰的影响,使得在516 Hz 处的脉冲干扰不满足严格的周期性,这些未被解析的频点最终会被当作随机干扰处理。

图6 定频和周期脉冲干扰的解析Fig.6 The resolution of constant and pulse Jamming
7.3 扫频干扰的解析
在扫频干扰解析前,先对时频矩阵进行数据平滑性的判断,若出现非平滑点,需要进行插值处理。在图7中的t=1.37 s、f =3250 Hz处给出了插值处理前后的仿真结果,可以看出,在t = [3.7 s,3.8 s]、f =[2200 Hz,2700 Hz]的时频区间内有较为复杂的二叉树结构。图8所示是通过基于二叉树结构的路径搜索算法对扫频干扰进行解析,基本能够得到较平滑的扫频图案。

图7 扫频干扰解析前Fig.7 The resolution of sweeping jamming

图8 解析得到的扫频干扰Fig.8 The sweeping jamming after resolution
7.4 随机干扰的解析
图9所示为对随机干扰的解析,由于前期频点单值化处理以及其他干扰解析过程中的误差累积等原因,会使得最终解析到的随机干扰与理论加载的随机干扰存在一定的误差,在下一部分中会通过时间占用度来表征和分析随机干扰整体的估计误差。
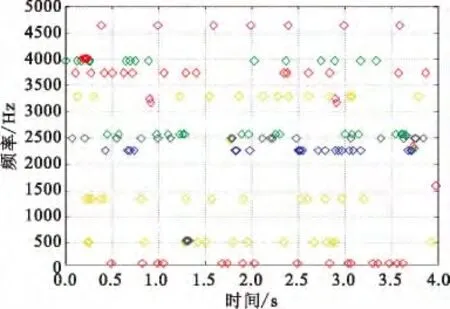
图9 随机干扰的解析Fig.9 The resolution of random disturbance
7.5 复合人为干扰解析误差的分析
7.5.1 定频干扰和周期脉冲干扰参数估计误差
在一定的干扰概率和不同时间占用度的随机干扰影响下,对定频干扰和周期脉冲干扰参数进行提取。参数提取的准确度使用相对误差来表征。分析结果可以看出,定频干扰和周期脉冲干扰估计误差几乎不受随机干扰的影响,一方面是由于随机干扰的频点干扰概率和干扰频点的时间占用度不够大,另一方面是由于STFT 算法的时频分辨率不能兼顾而造成的。
7.5.2 扫频干扰参数估计误差
扫频干扰参数的提取使用扫频频点估计的准确度来衡量。本文对扫频干扰的估计是采用基于二叉树结构的最短路径搜索算法,因此,随机干扰对扫频干扰趋势和路径的判断有很大影响,尤其是随机干扰与扫频趋势一致时,可能会超出二叉树结构的判断能力,使得扫频干扰估计错误。如图10所示,时间占用度取[0.05 0.1 0.15 0.2 0.25 0.3 0.35],频率占用度为0.15,且每种占用度情况下的随机干扰做50 次的蒙特卡洛仿真。结果表明,随着干扰时间占用度不断增加,扫频干扰估计的相对误差不断增大。
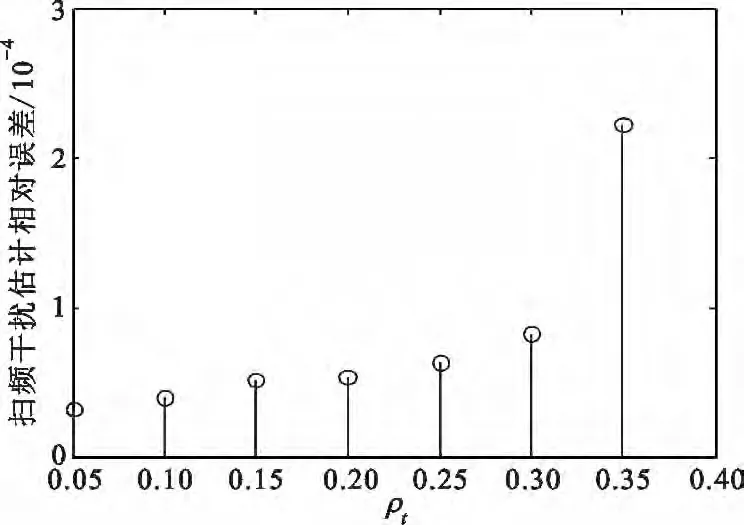
图10 扫频干扰估计误差Fig.10 The estimation of sweeping jamming
7.5.3 随机干扰时间占用度估计误差
在对扫频干扰自适应搜索过程中,有来自其他人为干扰相互间的影响,如定频干扰对扫频干扰的交叉干扰,随机干扰对路径搜索的影响,以及扫频干扰提取前进行的插值处理等。最终,各个人为干扰参数提取时伴随的误差以及插值处理的额外频点都以随机干扰的形式处理,所以,随机干扰时间占用度的估计可用来表征复合人为干扰参数估计总体的准确度。图11是随机干扰估计准确度的仿真,且每种占用度情况下的随机干扰做50 次的蒙特卡洛仿真。结果表明,随着理论时间占用度的增加,其估计误差与图10中扫频干扰估计误差有相似的增长趋势,而定频和周期脉冲干扰估计误差几乎不受随机干扰影响,所以,扫频干扰估计的准确度很大程度上决定了随机干扰占用度的估计误差。

图11 随机干扰估计误差Fig.11 The estimation of random disturbance
8 结束语
本文研究了军事无线通信中对蓄意人为干扰的识别和解析问题,构建了随机干扰影响下的复合人为干扰模型,通过短时傅里叶变换得到了干扰信号的时频矩阵,并结合通信频点的窄带带宽来确定短时傅里叶变换的时频分辨率;在干扰时频矩阵的基础上根据干扰信号参数特征的不同使用分类搜索算法对干扰信号解析。理论分析和实验结果表明,在一定复杂度的随机干扰的影响下,分类搜索算法能够较为准确地实现对复合干扰信号的解析。当然,文中仅是对干扰环境进行了分析,通信信号对干扰的分析也有很大的影响,如何在通信信号中准确地分析干扰信号,这需要下一步深入研究。
[1] Hopgood J R,Rayner J W.Single channel non-stationary stochastic signal separation using linear time-varying filters[J]. IEEE Transactions on Signal Processing,2003,51(7):1739-1752.
[2] 徐冠雷,王孝通,徐晓刚,等. 多分量到单分量可用EMD 分解的条件及判据[J].自然科学进展,2006,16(10):1356-1360.XU Guanlei,WANG Xiaotong,XU Xiaogang,et al. More component to the single component available EMD decomposition conditions and basis[J].Nature Science Development,2006,16(10):1356-1360.(in Chinese)
[3] 黄文通,李平杰. 成桥预拱度设置的正交多项式拟合法[J].公路工程,2013,38(5):103-107.HUANG Wentong,LI Pingjie. Orthogonal Polynomials’fitting For Setting Bridge Pre-Camber[J].Highway Engineering,2013,38(5):103-107.(in Chinese)
[4] 刘小峰,柏林,秦树人.基于自适应时频分解的瞬态冲击信号提纯[J].机械工程学报,2008,44(11):166-170.LIU Xiaofeng,BO Lin,QIN Shuren. Transient Impulse Signal Extraction Based on Self- adaptive Time- frequency Decomposition[J].Chinese Journal of Mechanical Engineering,2008,44(11):166-170.(in Chinese)
[5] 张睿.基于ICA 的工作模态参数识别及故障诊断方法研究[D].太原:中北大学,2014.ZHANG Rui.Operational Model Analysis and Fault Diagnosis Methods Based on ICA[D].Taiyuan:North University of China,2014.(in Chinese)
[6] NIU Yingtao,YAO Fuqiang,WANG Mingyue,et al. Anti-chirp-jamming communication based on the cognitive cycle[J]. International Journal of Electronics and Communications,2012,66(7):547-560.

